Blitzkurs Theoretische Informatik/ Grammatiken

Zusammenfassung

Natürliche Sprachen wie das Deutsche kann man nicht richtig beschreiben. Formale Sprachen beschreibt man mit Grammatiken. Das ist ein 4-Tupel bestehend aus der Menge der Nichtterminale, der Menge der Terminale, der Menge der Umformungsregeln und dem Startsymbol. Eine Ableitung vom Startsymbol bis zu einem Wort nur aus Terminalen kann man mit dem Ableitungspfeil oder als Ableitungsbaum aufschreiben. Gibt es für ein Wort unterschiedliche Ableitungsbäume, ist die Grammatik mehrdeutig. Gibt es für eine Sprache keine eindeutige Grammatik, ist sie inhärent mehrdeutig. Grammatiken und Sprachen unterteilt man nach der Chomsky-Hierarchie in Typ 0 (rekursiv aufzählbar), 1 (kontextsensitiv), 2 (kontextfrei) und 3 (regulär). Es gibt Sprachen, die nicht vom Typ 0 und damit nicht von Grammatiken beschreibbar sind.

Tag 1

Zusammenfassung

Das Gelernte über formale Sprachen trifft ebenso auf natürliche Sprachen zu. Es verschieben sich nur die Begriffe „Buchstabe“ und „Wort“ zu „Wort“ und „Satz“. Leider ist es kaum möglich, natürliche Sprachen formal zu beschreiben. Zur Beschreibung formaler Sprachen kommen Grammatiken zum Einsatz, die Regeln zur Ableitung von Wörtern aus Nichtterminalen enthalten. Normalerweise gibt man die Regeln in BNF an.

Vielleicht kommt dir eine Sache seltsam vor: Eine Sprache ist eine Menge von Wörtern. Das stimmt in der Theoretischen Informatik, aber es erscheint zunächst sinnlos, wenn man versucht, diese Definition auf natürlich gewachsene Sprachen zu übertragen. Nicht jeder Satz, der nur aus deutschen Wörtern besteht, ein Satz deutscher ist. Reihenfolge ist die wichtig.

Dieser Widerspruch löst sich schnell auf, wenn man erkennt, dass der Begriff „Wort“ in Bezug auf die Theorie der formalen Sprachen ungefähr vergleichbar ist mit dem umgangssprachlichen Begriff „Satz“. Es gehört also das Wort „Das ist ein deutscher Satz.“ zur Sprache $L_{\text{deutsch}},$ während „Könnte sein Satz das deutscher ein.“ nicht dazu gehört. „Satz“, „sein“, „könnte“ und so weiter sind dann Buchstaben des Alphabetes $\Sigma _{\text{deutsch}}.$ Das ABC hat aber nichts mit $\Sigma _{\text{deutsch}}$ zu tun, denn die Buchstaben braucht man nicht noch weiter zu teilen.

Es ist der Wunschtraum vieler Linguisten, natürliche Sprachen mit den Begriffen der Theoretischen Informatik formalisieren zu können und die Grenze zwischen formalen und natürlichen Sprachen aufzuheben. Eine vollständige Formalisierung einer Sprache ist unglaublich kompliziert, häufig überhaupt nicht möglich. Aber man kann tatsächlich relativ einfach gewisse Teilaspekte einer Sprache mathematisch korrekt definieren. Sieh dir dazu das folgende Beispiel an:
${\begin{aligned}&L_{Pron}=\{{\text{Er-, Sie-, Es-}}\},L_{Verb}=\{{\text{angelt-, baut-, n}}{\ddot {\text{a}}}{\text{ht-}}\},L_{Obj}=\{{\text{Blumen., Zierfische., Honig.}}\}\\&L_{deutsch}=L_{Pron}\cdot L_{Verb}\cdot L_{Obj}\end{aligned}}$

Die Wörter der hier beschriebenen Sprache $L_{\text{deutsch}}$ sind „Sie baut Honig.“, „Es angelt Blumen.“, „Er näht Zierfische.“ und viele mehr. Siebenundzwanzig grammatikalisch korrekte Sätze kann man bilden. Das sind natürlich längst nicht alle. Da das Deutsche wie andere Sprachen auch die Möglichkeit bietet, beliebig viele Nebensätze und Attribute einzuschieben, ist die Anzahl der richtig gebildeten deutschen Sätze sogar unendlich. Der französische Schriftsteller Marcel Proust ist für seine erhellenden Schachtelsätze berühmt. Der erste Satz aus dem Roman À l'ombre des jeunes filles en fleurs lautet:

„Ma mère, quand il fut question d'avoir pour la première fois M. de Norpois à dîner, ayant exprimé le regret que le Professeur Cottard fût en voyage et qu'elle-même eût entièrement cessé de fréquenter Swann, car l'un et l'autre eussent sans doute intéressé l'ancien Ambassadeur, mon père répondit qu'un convive éminent, un savant illustre, comme Cottard, ne pouvait jamais mal faire dans un dîner, mais que Swann, avec son ostentation, avec sa manière de crier sur les toits ses moindres relations, était un vulgaire esbrouffeur que le Marquis de Norpois eût sans doute trouvé selon son expression, «puant».“

Allein das Alphabet $\Sigma _{\text{deutsch}}$ ist eine unvorstellbar große Menge. Wenn man jedes zusammengesetzte Substantiv als einzelnen Buchstaben betrachtet, ist das Alphabet unendlich.  Donaudampfschiffahrtselektrizitätenhauptbetriebswerkbauunterbeamtengesellschaft ist noch lange nicht das Ende der Fahnenstange. Eine annähernd vollständige Formalisierung des Deutschen ist also wahrhaftig nicht in Sicht.

Es wird nun Zeit, zu erläutern, wie man Sprachen elegant beschreiben und einordnen kann. Bisher hast du zur Beschreibung einer Sprache mehr oder weniger alle Wörter aufgezählt. Wenn sich die Wörter ähneln, kann man zwar ökonomischer vorgehen, indem man die Konkatenation und Mengenoperatoren nutzt, aber es geht auch noch einfacher: Ebenso wie korrekt gebildete deutsche Sätze aus Einzelwörtern von grammatikalischen Regeln beschrieben werden, gibt es auch für die meisten formalen Sprachen, mit denen man es in der Praxis zu tun hat, Grammatiken, die die jeweilige Sprache hinreichend beschreiben.

Es gibt kurze Übersichten über die deutsche Grammatik und es gibt hundert Seiten lange Abhandlungen. Es gibt aber keine allumfassende systematische Beschreibung. Das liegt, wie oben gezeigt, daran, dass die deutsche Sprache sehr komplex ist und unzählige Besonderheiten und Ausnahmen aufweist, die sich mit Worten besser beschreiben lassen als mit mathematischen Symbolen. Oft genügt auch ein grober Überblick über einen Teilaspekt der Grammatik.

Wenn aber der Informatiker von einer Grammatik spricht, meint er eine vollständige Liste formalisierter eindeutiger Regeln zur Bildung von Wörtern im Sinne der Theoretischen Informatik (also Sätzen).

So könnte das Regelwerk einer Grammatik aussehen:

${\begin{aligned}&{\text{S}}\rightarrow \langle {\text{PRONOMEN, VERB, OBJEKT}}\rangle \\&{\text{PRONOMEN}}\rightarrow \langle {\text{E, r, -}}\rangle \\&{\text{PRONOMEN}}\rightarrow \langle {\text{S, i, e, -}}\rangle \\&{\text{PRONOMEN}}\rightarrow \langle {\text{E, s, -}}\rangle \\&{\text{VERB}}\rightarrow \langle {\text{a, n, g, e, l, t, -}}\rangle \\&{\text{VERB}}\rightarrow \langle {\text{b, a, u, t, -}}\rangle \\&{\text{VERB}}\rightarrow \langle {\text{n, }}{\ddot {\text{a}}}{\text{, h, t, -}}\rangle \\&{\text{OBJEKT}}\rightarrow \langle {\text{B, l, u, m, e, n, .}}\rangle \\&{\text{OBJEKT}}\rightarrow \langle {\text{Z, i, e, r, f, i, s, c, h, e, .}}\rangle \\&{\text{OBJEKT}}\rightarrow \langle {\text{H, o, n, i, g, .}}\rangle \end{aligned}}$

Es handelt sich um die Regeln einer Grammatik zur Bildung der oben beschriebenen vereinfachten deutschen Sprache. Die Bildung der Wörter geschieht folgendermaßen: Man fängt beim Startsymbol ${\text{S}}$ an. Das Wort hat zunächst die Länge drei: Es besteht aus den drei „Buchstaben“ ${\text{PRONOMEN, VERB}}$ und ${\text{OBJEKT.}}$ Die Großschreibung deutet an, dass es sich nicht um Buchstaben aus dem zugrundeliegenden Alphabet $\Sigma$ handelt. Diese Zeichen, man nennt sie Nichtterminale, müssen also noch durch richtige Buchstaben, so genannte Terminale, ersetzt werden. Zum Beispiel ist dort die Regel${\text{PRONOMEN}}\rightarrow \langle {\text{E, s, -}}\rangle .$ Wendet man sie an, lautet das Zwischenergebnis $\langle {\text{E, s, -, VERB, OBJEKT}}\rangle .$ Ein vollständig abgeleitetes Wort aus der Sprache, die von der Grammatik beschrieben wird, ist $\langle {\text{E, s, -, b, a, u, t, -, H, o, n, i, g, .}}\rangle .$ Insgesamt kann man siebenundzwanzig Wörter bilden.

Lasst uns die Sache an dieser Stelle gleich etwas vereinfachen! Die mathematisch korrekte Notation der Buchstabenfolgen mit den spitzen Klammern und den Kommata zwischen den Folgengliedern ist doch recht umständlich. Man legt normalerweise fest, dass alle Symbole optisch nur aus einem Buchstaben bestehen. Dann kann man sie lückenlos aneinander schreiben. Zum Beispiel so:

${\begin{aligned}&{\text{S}}\rightarrow {\text{PVO}}\\&{\text{P}}\rightarrow {\text{er-}}\\&{\text{P}}\rightarrow {\text{sie-}}\\&{\text{P}}\rightarrow {\text{es-}}\\&{\text{V}}\rightarrow {\text{angelt-}}\\&{\text{V}}\rightarrow {\text{baut-}}\\&{\text{V}}\rightarrow {\text{n}}{\ddot {\text{a}}}{\text{ht-}}\\&{\text{O}}\rightarrow {\text{blumen.}}\\&{\text{O}}\rightarrow {\text{zierfische.}}\\&{\text{O}}\rightarrow {\text{honig.}}\end{aligned}}$

Die Nichtterminale, also die Symbole, die noch abgeleitet werden müssen, werden mit Großbuchstaben dargestellt. Aus diesem Grunde sollten die Alphabete, über denen man Sprachen definiert, keine Großbuchstaben enthalten. Verwechslungen wären die Folge. Also Terminale sind normalerweise Kleinbuchstaben oder Ziffern. In diesem Fall kommt noch das Leerzeichen (als Bindestrich dargestellt) und der Punkt dazu.

Zur weiteren Vereinfachung kann man Ersetzungsregeln, deren linke Seiten identisch sind, mit vertikalen Strichen zusammenfassen. Zum Beispiel:

${\begin{aligned}&{\text{S}}\rightarrow {\text{PVO}}\\&{\text{P}}\rightarrow {\text{er-}}\mid {\text{sie-}}\mid {\text{es-}}\\&{\text{V}}\rightarrow {\text{angelt-}}\mid {\text{baut-}}\mid {\text{n}}{\ddot {\text{a}}}{\text{ht-}}\\&{\text{O}}\rightarrow {\text{blumen.}}\mid {\text{zierfische.}}\mid {\text{honig.}}\end{aligned}}$

Nach der Anwendung dieser Vereinfachungen sieht die Regelliste doch schon viel sympathischer aus. Wenn Produktionsregeln derart vereinfacht sind, spricht man von der Backus-Naur-Form (BNF) nach den Informatikern John Warner Backus und Peter Naur. Man gibt Regeln normalerweise in BNF an.

Übung

Mit welchen Produktionsregeln (in BNF) kann man die folgende Sprache beschreiben? Beginne mit dem nichtterminalen Symbol ${\text{S!}}$

$L=\lbrace {\text{eklig}}\rbrace \cup \lbrace {\text{furcht, wunder}}\rbrace \cdot \lbrace {\text{bar}}\rbrace$$\cup \lbrace {\text{sagen, lach, untersuchungs}}\rbrace \cdot \lbrace {\text{haft}}\rbrace$$\cup \lbrace {\text{klein, hoef, haess, mensch}}\rbrace \cdot \lbrace {\text{lich}}\rbrace$$\cup \lbrace {\text{energie, wasser}}\rbrace \cdot \lbrace {\text{einspar, verschwend, versorg}}\rbrace \cdot \lbrace {\text{ung}}\rbrace$

${\begin{aligned}&{\text{S}}\rightarrow {\text{eklig}}\mid {\text{Abar}}\mid {\text{Bhaft}}\mid {\text{Clich}}\mid {\text{DEung}}\\&{\text{A}}\rightarrow {\text{furcht}}\mid {\text{wunder}}\\&{\text{B}}\rightarrow {\text{sagen}}\mid {\text{lach}}\mid {\text{untersuchungs}}\\&{\text{C}}\rightarrow {\text{klein}}\mid {\text{hoef}}\mid {\text{haess}}\mid {\text{mensch}}\\&{\text{D}}\rightarrow {\text{energie}}\mid {\text{wasser}}\\&{\text{E}}\rightarrow {\text{einspar}}\mid {\text{verschwend}}\mid {\text{versorg}}\end{aligned}}$

Tag 2

Zusammenfassung

Eine Grammatik ist ein 4-Tupel aus $V,$ der Menge der Nichtterminale, $\Sigma ,$ dem Alphabet, $P,$ der Menge der Produktionsregeln und ${\text{S}}\in V,$ dem Startsymbol. Meistens gibt man aber nur $P$ an. Zur Definition der Regeln schreibt man den Definitionspfeil: $\rightarrow ,$ bei der Ableitung einer Satzform wird aber der Relationspfeil geschrieben: $\Rightarrow .$ Die Ableitungen können manchmal als Ableitungsbaum aufgeschrieben werden. Wenn es für ein vollständig abgeleitetes Wort nicht nur verschiedene Ableitungspfade, sondern auch noch unterschiedliche Ableitungsbäume gibt, ist die Grammatik mehrdeutig. Sprachen, die nicht mit einer eindeutigen Grammatik beschrieben werden können, sind inhärent mehrdeutig.

Eine einfache Liste von Ersetzungsregeln ist noch keine Grammatik. Es fehlt zum Beispiel die Information, welches Nichtterminal das Startsymbol ist. Man nennt es normalerweise ${\text{S,}}$ aber diese Information gehört unbedingt in die Beschreibung der Grammatik. Außerdem gehört das Alphabet, das die Sprache verwendet, und eine Auflistung aller Nichtterminale dazu. Man notiert eine Grammatik als 4-Tupel:
$G=\{V,\Sigma ,P,S\}$
Dabei ist $V$ die Menge aller Nichtterminale (Variablen), $\Sigma$ die Menge aller Terminale, also das Alphabet, $P$ die Menge aller Produktionsregeln und ${\text{S}}$ als Element von $V$ das Startsymbol.

Jetzt kann man weiter spezifizieren. Im gestern beschriebenen Fall gilt jetzt folgendes (die Wörter werden hier zur Vereinfachung als Buchstaben aufgefasst):

${\begin{aligned}&G_{\text{deutsch}}=&&\{V_{\text{deutsch}},\Sigma _{\text{deutsch}},P_{\text{deutsch}},{\text{S}}\}\\&V_{\text{deutsch}}=&&\{{\text{S, P, V, O}}\}\\&\Sigma _{\text{deutsch}}=&&\{{\text{er-, sie-, es-, angelt-, baut-, n}}{\ddot {\text{a}}}{\text{ht-, blumen., zierfische., honig.}}\}\\&P_{\text{deutsch}}=&&\{{\text{S}}\rightarrow {\text{PVO}}\\&&&{\text{P}}\rightarrow {\text{er-}}\mid {\text{sie-}}\mid {\text{es-}}\\&&&{\text{V}}\rightarrow {\text{angelt-}}\mid {\text{baut-}}\mid {\text{n}}{\ddot {\text{a}}}{\text{ht-}}\\&&&{\text{O}}\rightarrow {\text{blumen.}}\mid {\text{zierfische.}}\mid {\text{honig.}}\}\end{aligned}}$

Die Grammatik $G_{\text{deutsch}}$ ist jetzt ausreichend beschrieben und die Sprache, die diese Grammatik bildet, $L(G_{\text{deutsch}})=L_{\text{deutsch}},$ ist genau die genannte Sprache aus siebenundzwanzig deutschen Sätzen.

Wenn man mit Grammatiken rechnet und sie vergleicht, braucht man diese Formalien. Definiert man zum Beispiel zwei Grammatiken als $G_{1}=\{V_{1},\Sigma ,P_{1},S_{1}\}$ und $G_{2}=\{V_{2},\Sigma ,P_{2},S_{2}\},$ dann ist klar, dass beide die gleiche Terminalenmenge verwenden. Wenn man aber eine einzelne Grammatik angeben möchte, dann schreibt man normalerweise nur die Produktionsregeln vollständig in BNF auf und spart sich den Rest. Man weiß ja, dass ${\text{S}}$ das Startsymbol ist und man sieht ja, welche die relevanten Elemente von $V$ und $\Sigma$ sind.

Wie wendet man denn nun eine Grammatik richtig an? Das Ziel ist es, aus dem Nichts Wörter zu erschaffen. Formal ausgedrückt: Das Startsymbol wird zu einer Folge von Terminalen abgeleitet. Ableiten heißt, die Regeln anzuwenden. Nach der obigen Beispielgrammatik kann ${\text{S}}$ zunächst nur folgendermaßen abgeleitet werden: ${\text{S}}\Rightarrow _{G}{\text{PVO,}}$ wobei der Pfeil mit zwei horizontalen Linien wichtig ist. Für den nächsten Ableitungsschritt gibt es aber mehrere Möglichkeiten. Man könnte zum Beispiel schreiben ${\text{PVO}}\Rightarrow _{G}{\text{sie-VO}}$ oder ${\text{PVO}}\Rightarrow _{G}{\text{PVzierfische.}}$ In jedem Ableitungsschritt wird genau eine Regel aus $G$ angewendet. Welche, ist egal. Man spricht diesen Doppelpfeil als „${\text{S}}$ geht unter $G$ unmittelbar über in ${\text{PVO.}}$“ aus. Dieser Relationspfeil ist vom Definitionspfeil, der in den Produktionsregeln vorkommt, abzugrenzen: ${\text{S}}\rightarrow {\text{PVO}}$ spricht man „${\text{S}}$ ist definiert als ${\text{PVO.}}$“ aus. Während diese Definition allgemeingültig ist, kann die Ableitung vom Startsymbol über verschiedene Satzformen bis zu einem Wort $w\in \Sigma ^{\star }$ beliebig verlaufen, sofern die Produktionsregeln gewisse Variationsmöglichkeiten offenhalten. Zwei mögliche Ableitungen sind
${\text{S}}\Rightarrow {\text{PVO}}\Rightarrow {\text{sie-VO}}\Rightarrow {\text{sie-angelt-O}}\Rightarrow {\text{sie-angelt-honig.}}$
und
${\text{S}}\Rightarrow {\text{PVO}}\Rightarrow {\text{PVzierfische.}}\Rightarrow {\text{Pbaut-zierfische.}}\Rightarrow {\text{sie-baut-zierfische.}}$
Die Angabe, unter welcher Grammatik die Relation gilt – den tiefgestellten Buchstaben rechts vom Ableitungspfeil – kann man großzügig weglassen, wenn es sowieso nur um eine einzelne Grammatik geht.

Manche Grammatiken erlauben eine übersichtlichere Darstellung solcher Ableitungen:

Dieser Ableitungsbaum gehört sowohl zu der Ableitung
${\text{S}}\Rightarrow {\text{PVO}}\Rightarrow {\text{sie-VO}}\Rightarrow {\text{sie-angelt-O}}\Rightarrow {\text{sie-angelt-honig.}}$
als auch zu
${\text{S}}\Rightarrow {\text{PVO}}\Rightarrow {\text{PVhonig.}}\Rightarrow {\text{Pangelt-honig.}}\Rightarrow {\text{sie-angelt-honig.}}$
Egal, ob man die Linksableitung oder die Rechtsableitung bevorzugt, es gibt zu jedem Wort $w\in L(G)$ nur genau einen Ableitungsbaum. Man sagt, die Grammatik ist eindeutig. Eine mehrdeutige Grammatik ist demgegenüber die folgende:

${\begin{aligned}&{\text{S}}\rightarrow {\text{AB}}\\&{\text{A}}\rightarrow {\text{ab}}\mid {\text{abc}}\\&{\text{B}}\rightarrow {\text{d}}\mid {\text{cd}}\end{aligned}}$

Man kann nun wieder verschiedene Ableitungen für das Wort „abcd“ finden:
${\text{S}}\Rightarrow {\text{AB}}\Rightarrow {\text{abB}}\Rightarrow {\text{abcd}}$
und
${\text{S}}\Rightarrow {\text{AB}}\Rightarrow {\text{abcB}}\Rightarrow {\text{abcd.}}$
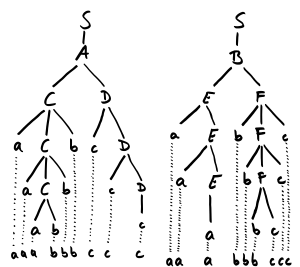
Der Haken ist, dass auch die Ableitungsbäume verschieden sind:

Die Grammatik ist mehrdeutig. Diese Mehrdeutigkeit kann man auch auf Sprachen übertragen. Man bezeichnet eine Sprache als inhärent mehrdeutig, wenn es nicht möglich ist, eine eindeutige Grammatik für diese Sprache zu finden. Heißt die oben angegebene mehrdeutige Grammatik $G,$ dann ist die Sprache
$L(G)=\{{\text{abd, abcd, abccd}}\}$
aber nicht inhärent mehrdeutig, denn man kann eine eindeutige Grammatik angeben:

${\begin{aligned}&{\text{S}}\rightarrow {\text{abC}}\\&{\text{C}}\rightarrow {\text{d}}\mid {\text{cd}}\mid {\text{ccd}}\end{aligned}}$

Jetzt gibt es für jedes Wort $w\in L(G)$ nur eine Ableitung und damit auch nur einen Ableitungsbaum. $G$ ist eindeutig.

Übung

Gib eine vollständige Beschreibung einer Grammatik $G$ für die folgende Sprache an!

$L(G)=\lbrace {\text{eklig}}\rbrace \cup \lbrace {\text{furcht, wunder}}\rbrace \cdot \lbrace {\text{bar}}\rbrace \cup \lbrace {\text{sagen, lach, untersuchungs}}\rbrace \cdot \lbrace {\text{haft}}\rbrace \cup \lbrace {\text{klein, hoef, haess, mensch}}\rbrace \cdot \lbrace {\text{lich}}\rbrace \cup \lbrace {\text{energie, wasser}}\rbrace \cdot \lbrace {\text{einspar, verschwend, versorg}}\rbrace \cdot \lbrace {\text{ung}}\rbrace$

${\begin{aligned}&G=&&\{V,\Sigma ,P,{\text{S}}\}\\&V=&&\{{\text{S, A, B, C, D, E}}\}\\&\Sigma =&&\{{\text{bar, einspar, eklig, energie, furcht, haess, haft, hoef, klein, lach, lich, mensch, sagen, ung, untersuchungs, verschwend, versorg, wasser, wunder}}\}\\&P=&&\{{\text{S}}\rightarrow {\text{eklig}}\mid {\text{Abar}}\mid {\text{Bhaft}}\mid {\text{Clich}}\mid {\text{DEung}}\\&&&{\text{A}}\rightarrow {\text{furcht}}\mid {\text{wunder}}\\&&&{\text{B}}\rightarrow {\text{sagen}}\mid {\text{lach}}\mid {\text{untersuchungs}}\\&&&{\text{C}}\rightarrow {\text{klein}}\mid {\text{hoef}}\mid {\text{haess}}\mid {\text{mensch}}\\&&&{\text{D}}\rightarrow {\text{energie}}\mid {\text{wasser}}\\&&&{\text{E}}\rightarrow {\text{einspar}}\mid {\text{verschwend}}\mid {\text{versorg}}\}\end{aligned}}$

Tag 3

Zusammenfassung

Die Chomsky-Hierarchie unterteilt die Grammatiken. Die meisten Grammatiken sind vom Typ 0, einige außerdem vom Typ 1. Die Einschränkung für Typ-1-Grammatiken (kontextsensitive) ist $|w_{1}|\leq |w_{2}|$ für alle $(w_{1}\rightarrow w_{2})\in P.$ Das Wortproblem ist für Typ-1-Grammatiken entscheidbar. Typ-1-Grammatiken sind darüberhinaus vom Typ 2 (kontextfrei), wenn für alle $(w_{1}\rightarrow w_{2})\in P$ gilt $w_{1}\in V.$ Das Leerheitsproblem ist für Typ-2-Grammatiken entscheidbar; es gibt einen effizienten Algorithmus für Typ-2-Grammatiken, die in CNF vorliegen.

Es bietet sich an, Sonderfälle von Grammatiken zu untersuchen. Für viele Grammatiken, mit denen man in der Praxis häufig zu tun hat, gelten gewisse Regeln, die einem das Leben vereinfachen, die man aber leider nicht auf alle Grammatiken übertragen kann. Noam Chomsky, ein Linguist und Libertärer, klassifizierte die Grammatiken nach ihrer Handhabbarkeit. Nach seiner Einteilung sind alle Grammatiken vom Typ 0. Es gibt einige, die nicht nur vom Typ 0, sondern auch vom Typ 1 sind. Eine Typ-1-Grammatik zeichnet sich dadurch aus, dass man nicht nur Wörter, die der beschriebenen Sprache angehören, generieren kann, sondern auch umgekehrt feststellen kann, ob ein gegebenes Wort irgendwie von dieser Grammatik erzeugt werden kann. Die Einschränkung für Typ-1-Grammatiken besteht darin, dass die linke Seite jeder Produktionsregel höchstens genauso lang ist wie die dazugehörige rechte Seite. Dazu ein Beispiel:

${\begin{aligned}&{\text{S}}\rightarrow {\text{ABABAB}}\mid {\text{SAB}}\\&{\text{BA}}\rightarrow {\text{a}}\\&{\text{Aa}}\rightarrow \varepsilon \\&{\text{aB}}\rightarrow \varepsilon \end{aligned}}$

Das sind fünf Regeln. Bei den letzten dreien besteht die linke Seite aus mehr Symbolen als die rechte Seite. $\varepsilon$ ist in diesem Sinne kein Symbol. Es hat ja die Länge 0. Es ist deshalb möglich – in diesem Falle sogar zwingend nötig –, dass die Länge der Satzformen während der Ableitung nicht immer nur ansteigt. Denkbar ist der folgende Ableitungsschritt: ${\text{ABABAB}}\Rightarrow {\text{AaBAB.}}$ Die Anzahl der Symbole sinkt hier von sechs auf fünf. Dagegen ist diese Grammatik vom Typ 1:
${\text{S}}\rightarrow {\text{ab}}\mid {\text{aSb}}$
Die Ableitung eines Wortes weist immer die folgende Struktur auf: ${\text{S}}\Rightarrow {\text{aSb}}\Rightarrow {\text{aaSbb}}\Rightarrow {\text{aaaSbbb}}\Rightarrow {\text{aaaabbbb.}}$
Da keine linken Seiten der Produktionsregeln länger sind als die rechten Seiten, werden die Satzformen während der Ableitung niemals wieder kürzer.

Wenn man nun wissen will, ob ein Wort von einer Typ-1-Grammatik gebildet werden kann, probiert man einfach systematisch alle möglichen Ableitungen aus, ausgehend vom Startsymbol. Wenn man die Länge des gegebenen Wortes überschritten hat, kann man aufhören, denn aus einer längeren Satzform kann das Wort nicht gebildet werden. Lass uns probieren, ob die oben angegebene Grammatik das Wort „aaabbb“ bilden kann. Bei der folgenden Grafik handelt es sich nicht um einen Ableitungsbaum.

Hier sind alle möglichen Satzformen dargestellt, die höchstens sechs Zeichen lang sind. Tatsächlich ist das gesuchte Wort darunter. Das Wortproblem, wie es in Fachkreisen genannt wird, ist für Typ-1-Grammatiken lösbar.

Es gibt nun wiederum Typ-1-Grammatiken, die darüber hinaus als Typ-2-Grammatiken bezeichnet werden. Eine Grammatik ist vom Typ 2, wenn alle linken Seiten der Umformungsregeln aus genau einem Nichtterminal bestehen. Die oben beispielhaft verwendete Typ-1-Grammatik
${\text{S}}\rightarrow {\text{ab}}\mid {\text{aSb}}$
ist also auch vom Typ 2. Es sind zwei Regeln. Die linke Seite ist in beiden Fällen nur das Startsymbol ${\text{S.}}$

Erkennt man, dass eine Grammatik vom Typ 2 ist, kommt man in den Genuss einiger komfortabler Erleichterungen, die leider nicht generell gelten. Zum Beispiel kann man für Typ-2-Grammatiken entscheiden, ob die erzeugte Sprache leer ist. Die Sprache, die die folgende Grammatik erzeugt, ist die leere Menge:

${\begin{aligned}&{\text{S}}\rightarrow {\text{AB}}\\&{\text{B}}\rightarrow {\text{CC}}\\&{\text{A}}\rightarrow {\text{CD}}\\&{\text{D}}\rightarrow {\text{AA}}\\&{\text{C}}\rightarrow {\text{a}}\end{aligned}}$

Diese Grammatik liegt in Chomsky-Normalform (CNF) vor: Alle Regeln haben die Struktur ${\text{A}}\rightarrow {\text{BC}}$ bzw. ${\text{A}}\rightarrow {\text{a.}}$ Alle Typ-2-Grammatiken lassen sich in CNF umformen. An solch einer Normalform kann man leicht überprüfen, ob die generierte Sprache leer ist.

Wie kommt man nun darauf? Das Ziel ist es ja, aus dem Startsymbol Satzformen abzuleiten, die nur aus Terminalzeichen bestehen. Man markiert also alle Regeln der Form ${\text{A}}\rightarrow {\text{a,}}$ denn nur diese bilden am Ende der Ableitungsbäume die Wörter der Sprache. Diese Grammatik hat nur eine solche Regel: ${\text{C}}\rightarrow {\text{a.}}$ Als nächstes markiert man alle Regeln der Form ${\text{A}}\rightarrow {\text{BC,}}$ wobei ${\text{B}}$ und ${\text{C}}$ schon linke Seiten markierter Regeln sind. In diesem Fall kommt dafür nur ${\text{B}}\rightarrow {\text{CC}}$ in Frage. Man weiß jetzt, dass man nicht nur aus ${\text{C,}}$ sondern auch aus ${\text{B}}$ Terminale bilden kann. Den letzten Schritt wiederholt man so lange, bis man keine weitere Regel mehr markieren kann. Dieser Punkt ist bei dieser Grammatik jetzt schon erreicht. Unter den markierten Regeln ist aber keine mit dem Startsymbol auf der linken Seite. Das heißt, es gibt keinen von ${\text{S}}$ ausgehenden Ableitungspfad, der zu einem Wort führt, das nur aus Terminalen besteht. Die erzeugte Sprache ist leer.

Typ-2-Grammatiken nennt man auch kontextfrei, denn die Ersetzung eines Terminals hängt nicht von den umgebenden Symbolen ab. In einer Typ-1-Grammatik – einer kontextsensitiven Grammatik – kann es auch solch eine Regel geben:
${\text{aAb}}\rightarrow {\text{aBCb.}}$
Das heißt, ${\text{A}}$ kann nur dann durch ${\text{BC}}$ ersetzt werden, wenn es in einem gewissen Kontext steht; wenn es von ${\text{a}}$ und ${\text{b}}$ eingeschlossen ist. Eine Grammatik, bei der der Kontext keine Rolle spielt, ist programmiertechnisch leichter umzusetzen. Deshalb widmete Noam Chomsky den kontextfreien Grammatiken einen eigenen Typ in seiner Hierarchie.

Übung

Für welche Grammatiken kann man Ableitungsbäume aufstellen?

Nur für kontextfreie. Da jeder Knoten des Baumes nur ein Nichtterminal und jedes Blatt nur ein Terminal ist, kann man keinen Ableitungsbaum für eine Ableitung aufstellen, bei der mehrere Symbole auf einmal ersetzt werden.

---

Ist die folgende Grammatik leer?

${\begin{aligned}&{\text{S}}\rightarrow {\text{AB}}\mid {\text{BC}}\\&{\text{A}}\rightarrow {\text{AA}}\mid {\text{BB}}\\&{\text{B}}\rightarrow {\text{0}}\\&{\text{C}}\rightarrow {\text{1}}\end{aligned}}$

Sie ist nicht leer. Es gibt die Regel ${\text{S}}\rightarrow {\text{BC}}$ und ${\text{B}}$ und ${\text{C}}$ lassen sich zu Terminalen ableiten. Die Sprache enthält das Wort „01“ neben unendlich vielen anderen.

Tag 4

Zusammenfassung

Manche kontextfreien Grammatiken sind außerdem regulär (Typ 3). Die Einschränkung für reguläre Grammatiken ist, dass alle Produktionsregeln die Form ${\text{A}}\rightarrow {\text{a}}$ bzw. ${\text{A}}\rightarrow {\text{aB}}$ haben, wobei ${\text{a}}$ ein Terminal und ${\text{A}}$ und ${\text{B}}$ Nichtterminale sind. Das Äquivalenzproblem ist lösbar. Das Wortproblem ist, im Gegensatz zu anderen kontextsensitiven Grammatiken, effizient lösbar.

Die Chomsky-Hierarchie besteht aus vier Grammatiktypen. Die Typen 0 bis 2 kennst du schon. Jetzt fehlt nur noch Typ 3. Die Menge der Typ-3-Grammatiken ist nun wieder eine Teilmenge der Menge der Typ-2-Grammatiken. Es gibt also kontextfreie Grammatiken, die zusätzlich regulär sind. Die Regeln von Typ-3-Grammatiken haben auf der linken Seite nur ein Nichtterminal, weil es sich um Typ-2-Grammatiken handelt. Außerdem gibt es keine $\varepsilon$-Regeln, weil sie auch Typ-1-Grammatiken sind und deshalb die linken Seiten nicht länger als die rechten Seiten der Produktionsregeln sein dürfen. Die besondere Einschränkung für reguläre gegenüber allen anderen kontextfreien Grammatiken ist nun, dass die rechten Seiten entweder ein Terminal oder ein Terminal und ein Nichtterminal sein müssen. Alle Regeln haben also die Struktur ${\text{A}}\rightarrow {\text{a}}$ oder ${\text{A}}\rightarrow {\text{aB.}}$ Man kann entweder die Form ${\text{A}}\rightarrow {\text{aB}}$ oder ${\text{A}}\rightarrow {\text{Ba}}$ zulassen. Die Menge der Sprachen, die von solchen Grammatiken beschrieben werden können, bleibt die gleiche. Es herrscht weitgehend Einigkeit darüber, dass die Regeln die Form ${\text{A}}\rightarrow {\text{aB}}$ haben. Ganz wichtig ist aber, dass man innerhalb einer Grammatik nicht die Varianten mischt, denn dann ist es keine reguläre Grammatik mehr.

Für reguläre Grammatiken ist das Äquivalenzproblem lösbar. Das heißt, die Fragestellung, ob zwei gegebene Grammatiken genau die gleiche Sprache erzeugen, lässt sich beantworten, sofern es sich um reguläre Grammatiken handelt. Eine weitere Eigenschaft regulärer Grammatiken ist, dass das Wortproblem nicht nur entscheidbar ist, sondern das auch noch sehr effizient. Entscheidbar ist das Problem ja generell für kontextsensitive Grammatiken. Aber für reguläre Grammatiken gibt es sehr schnelle Algorithmen, die feststellen, ob ein gegebenes Wort Element der Sprache ist oder nicht.

Es folgt eine zusammenfassende Darstellung der Chomsky-Hierarchie:

• Typ-0- oder rekursiv aufzählbare Grammatiken (keine Einschränkungen)
  • Typ-1- oder kontextsensitive Grammatiken (Für alle Ableitungen $w_{1}\Rightarrow w_{2}$ bzw. Produktionsregeln $w_{1}\rightarrow w_{2}$ gilt $|w_{1}|\leq |w_{2}|.$)
    • Typ-2- oder kontextfreie Grammatiken (Für alle Produktionsregeln $w_{1}\rightarrow w_{2}$ gilt $w_{1}\in V.$)
      • Typ-3- oder reguläre Grammatiken (Für alle Produktionsregeln $w_{1}\rightarrow w_{2}$ gilt $w_{1}\in V,w_{2}\in \Sigma \cup \Sigma \cdot V.$)

Übung

Ist die folgende Sprache mit einer regulären Grammatik beschreibbar?

$L(G)=\{{\text{01, 11110, 10101, 000}}\}$

Ja. Sie kann mit der folgenden regulären Grammatik beschrieben werden:

${\begin{aligned}&{\text{S}}\rightarrow {\text{0A}}\mid {\text{1B}}\mid {\text{1C}}\mid {\text{0D}}\\&{\text{A}}\rightarrow {\text{1}}\\&{\text{B}}\rightarrow {\text{1E}}\\&{\text{E}}\rightarrow {\text{1F}}\\&{\text{F}}\rightarrow {\text{1G}}\\&{\text{G}}\rightarrow {\text{0}}\\&{\text{C}}\rightarrow {\text{0H}}\\&{\text{H}}\rightarrow {\text{1K}}\\&{\text{K}}\rightarrow {\text{0A}}\\&{\text{D}}\rightarrow {\text{0G}}\\\end{aligned}}$

Alle Sprachen mit nur endlich vielen Wörtern lassen sich mit regulären Grammatiken beschreiben.

Tag 5

Zusammenfassung

Es gibt keine Grammatiken, die nicht vom Typ 0 sind, aber es gibt Sprachen, die nicht von Typ-0-Grammatiken beschrieben werden können. Die Typen überträgt man auch auf Sprachen.

Die Begriffe rekursiv aufzählbar, kontextsensitiv, kontextfrei und regulär bezieht man auch auf Sprachen, die von solchen Grammatiken erzeugt werden. Erst hier wird der Typ 0 sinnvoll. Es gibt nämlich durchaus Sprachen, die nicht von Grammatiken beschrieben werden können. Das sind genau die Sprachen, die eben nicht vom Typ 0 und nicht rekursiv aufzählbar sind. Es gibt einen schönen Beweis für diese Behauptung:

Sprachen sind meistens unendliche Mengen. Endliche Sprachen, also solche, die nur eine bestimmte Anzahl an Wörtern enthalten, sind immer regulär, denn man kann sie mit einer regulären Grammatik beschreiben. Für Nicht-Typ-0-Sprachen kommen also tatsächlich nur unendliche Sprachen in Frage. Der Kern jeder Grammatik, die Menge der Produktionsregeln, ist aber stets eine endliche Menge. Es gibt keine Grammatik mit unendlich vielen Regeln, denn sonst könnte man diese nicht direkt aufschreiben, sondern müsste sie auch wieder mittels einer Grammatik definieren. Hier dreht sich die Überlegung im Kreis. Im Endeffekt ist jede Grammatik endlich. Die Menge aller Grammatiken ist zwar unendlich, aber rekursiv aufzählbar. Man kann also irgendwo anfangen und systematisch alle Grammatiken aufzählen, obwohl man mit dieser Aufgabe nie fertig würde. Im Gegensatz dazu kann man aber die Menge aller Sprachen als Menge von unendlichen Objekten nicht systematisch aufzählen. Es ist, als würde man versuchen, alle reellen Zahlen aufzuzählen. Es geht noch nicht einmal in einem bestimmten Intervall. Deshalb ist es nicht möglich, jeder Grammatik eine Sprache zuzuordnen und umgekehrt. Es gibt unendlich viele Grammatiken und es gibt unendlich viele Sprachen. Aber dennoch gibt es mehr Sprachen als Grammatiken. Es gibt Sprachen, die nicht von Grammatiken beschrieben werden können. Die, die von Typ-0-Grammatiken beschrieben werden können, heißen rekursiv aufzählbare Sprachen.

In den folgenden Wochen wirst du mehr über reguläre, kontextfreie, kontextsensitive und rekursiv aufzählbare Sprachen lernen.

Übung

Die Menge der natürlichen Zahlen (beginnend mit 0) ist rekursiv aufzählbar. Entwickle ein System, die natürlichen Zahlen so aufzuzählen, dass du in der Unendlichkeit theoretisch alle genannt hättest.

0, 1, 2, 3, 4, …

---

Die folgenden Mengen sind ebenfalls rekursiv aufzählbar. Entwickle ähnliche Systeme.

• die Quadratzahlen
• die ganzen Zahlen
• die Wörter, die aus den Buchstaben a, b und c bestehen

• 0, 1, 4, 9, 16, …
• 0, 1, −1, 2, −2, 3, −3, …
• ε, a, b, c, aa, ab, ac, ba, bb, bc, ca, cb, cc, aaa, aab, aac, aba, …

Rückblick

Lies dir heute die Zusammenfassungen noch einmal durch. Wenn du sehr viel Zeit und Lust hast, kannst du natürlich auch alles lesen. Gehe kurz die Übungen der vergangenen Tage durch und versuche dich dann an diesen:

Übung

Gib den Typ dieser Grammatik an:

${\begin{aligned}&{\text{S}}\rightarrow {\text{A}}\mid {\text{B}}\mid \varepsilon \\&{\text{A}}\rightarrow {\text{CD}}\mid {\text{C}}\mid {\text{D}}\\&{\text{B}}\rightarrow {\text{EF}}\mid {\text{E}}\mid {\text{F}}\\&{\text{C}}\rightarrow {\text{aCb}}\mid {\text{ab}}\\&{\text{D}}\rightarrow {\text{cD}}\mid {\text{c}}\\&{\text{E}}\rightarrow {\text{aE}}\mid {\text{a}}\\&{\text{F}}\rightarrow {\text{bFc}}\mid {\text{bc}}\end{aligned}}$

Alle linken Seiten sind ausschließlich einzelne Nichtterminale. Es handelt sich also um eine kontextfreie Grammatik. Den Einschränkungen für reguläre Grammatiken entspricht diese aber nicht. Man kann genauer sagen: Es ist eine kontextfreie, nicht reguläre Grammatik.

---

Zeichne einen Ableitungsbaum für das Wort „aaabbbccc“. Ist die Grammatik mehrdeutig? Dann zeichne auch alle anderen Ableitungsbäume für dieses Wort.

Das sind die beiden möglichen Ableitungsbäume. Die Grammatik ist also mehrdeutig. Die Sprache, die sie beschreibt, ist sogar inhärent mehrdeutig.