Blitzkurs Theoretische Informatik/ reguläre Sprachen

Zusammenfassung

Reguläre Ausdrücke, deterministische und nichtdeterministische endliche Automaten und reguläre Grammatiken sind äquivalente Beschreibungsmöglichkeiten für reguläre Sprachen. Reguläre Sprachen sind unter allen bekannten Rechenoperationen abgeschlossen. Das Wortproblem ist effizient lösbar.

Tag 1

Zusammenfassung

Reguläre Ausdrücke sind alle Kombinationen von Vereinigungen, Konkatenationen und Sternbildungen von Terminalen. Die regulären Ausdrücke beschreiben genau die regulären Sprachen. Das lässt sich über die Abschlusseigenschaften beweisen: Reguläre Sprachen sind unter Vereinigung, Konkatenation, Kleene-Stern und Potenzierung abgeschlossen.

In der ersten Wochenlektion, als dir Grammatiken noch nicht bekannt waren, wurden Sprachen nur als Mengen von Wörtern und deren Vereinigungen und Konkatenationen dargestellt. Auf diese Weise kann man nur einen geringen Teil der Sprachen überhaupt definieren. Die Sprache, die alle Wörter über dem Alphabet $\Sigma _{b}=\{0,1\}$ enthält, deren letztes oder vorletztes Zeichen eine 1 ist, kann man zum Beispiel folgendermaßen darstellen:
$L=\{0,1\}^{\star }\cdot \{1\}\cup \{0,1\}^{\star }\cdot \{1\}\cdot \{0,1\}$
Demgegenüber lässt sich die Sprache über dem gleichen Alphabet, deren Wörter gleich viele Nullen wie Einsen enthalten, nicht auf diese einfache Weise eindeutig definieren, sondern nur mithilfe einer Grammatik:

${\begin{aligned}&{\text{S}}\rightarrow \varepsilon \mid {\text{C}}\\&{\text{C}}\rightarrow {\text{0A}}\mid {\text{1B}}\\&{\text{A}}\rightarrow {\text{1}}\mid {\text{1C}}\mid {\text{0AA}}\\&{\text{B}}\rightarrow {\text{0}}\mid {\text{0C}}\mid {\text{1BB}}\end{aligned}}$

Es handelt sich um eine kontextfreie Grammatik. Über die $\varepsilon$-Regel ${\text{S}}\rightarrow \varepsilon ,$ die eigentlich die Bedingung $|w_{1}|\leq |w_{2}|$ für kontextsensitive Grammatiken verletzt, kann man hier hinwegsehen, da diese Produktionsregel nur das leere Wort noch in die Sprache mit aufnimmt und ${\text{S}}$ auf keiner rechten Seite vorkommt. Wäre man ganz pedantisch, könnte man diese Regel auch weglassen.

Die weiter oben genannte Sprache, deren Wörter auf „10“, „11“ oder „01“ enden, kann auch mittels der folgenden Grammatik beschrieben werden:

${\begin{aligned}&{\text{S}}\rightarrow {\text{0S}}\mid {\text{1A}}\mid {\text{1}}\\&{\text{A}}\rightarrow {\text{0B}}\mid {\text{1A}}\mid {\text{0}}\mid {\text{1}}\\&{\text{B}}\rightarrow {\text{0S}}\mid {\text{1A}}\mid {\text{1}}\end{aligned}}$

Es handelt sich hier offensichtlich um eine reguläre Grammatik. Man kann sogar verallgemeinern: Alle Sprachen, die aus endlichen Mengen von Terminalzeichen mittels der bekannten Rechenoperationen gebildet werden können, lassen sich mit regulären Grammatiken beschreiben und sind damit regulär. Diese zunächst vage erscheinende Aussage soll im Folgenden bewiesen werden. Keine Angst! Das tut nicht weh.

Endliche Mengen von Terminalzeichen sind ja nichts anderes als endliche Mengen von Wörtern der Länge 1. Mengen von Wörtern sind Sprachen und endliche Sprachen, also endliche Mengen von Wörtern, sind immer reguläre Sprachen. Das weißt du alles schon. Wenn man zwei endliche Sprachen vereinigt, ist das Ergebnis immer noch eine endliche Sprache. Man nimmt sich einfach die Wörter beider Sprachen, schreibt sie zwischen ein Paar geschweifter Klammern und hat bewiesen, dass die endlichen Sprachen unter Vereinigung abgeschlossen sind. Wenn Mathematiker sagen wollen, dass eine Operation, angewendet auf Elemente einer Menge, immer wieder nur Elemente dieser Menge zum Ergebnis hat, dann sprechen sie vom „Abschluss“ dieser Menge unter dieser Operation.

Endliche Sprachen sind also unter Vereinigung abgeschlossen. Eigentlich geht es hier aber um die viel größere Klasse der regulären Sprachen. Reguläre Sprachen können ja auch unendlich sein. Sind auch sie unter Vereinigung abgeschlossen? Das einfachste ist es wohl, es auszuprobieren. Man nehme sich zwei reguläre Grammatiken $G_{1}$ und $G_{2},$ wobei man allen Nichtterminalen in $G_{1}$ eine tiefgestellte 1 und allen Nichtterminalen in $G_{2}$ eine 2 verpasst. Etwa so:

${\begin{aligned}&G_{1}:&&{\text{S}}_{1}\rightarrow {\text{aA}}_{1}\mid {\text{bB}}_{1}\\&&&{\text{A}}_{1}\rightarrow {\text{aA}}_{1}\mid {\text{a}}\\&&&{\text{B}}_{1}\rightarrow {\text{bB}}_{1}\mid {\text{b}}\\&G_{2}:&&{\text{S}}_{2}\rightarrow {\text{a}}\mid {\text{bA}}_{2}\mid {\text{cA}}_{2}\\&&&{\text{A}}_{2}\rightarrow {\text{bA}}_{2}\mid {\text{cA}}_{2}\mid {\text{b}}\mid {\text{c}}\end{aligned}}$

Diese beiden regulären Grammatiken definieren zwei unendliche reguläre Sprachen, nämlich
$L(G_{1})=\{{\text{aa, aaa, aaaa,}}\ldots ,{\text{bb, bbb, bbbb,}}\ldots \}$ und
$L(G_{2})=\{{\text{a, bb, bc, cb, cc, bbb, bbc, bcb,}}\ldots \}.$
Es ist nun eine – bitteschön reguläre – Grammatik zu finden, die die Vereinigung beider Sprachen erzeugt. Dazu übernimmt man die Regelwerke der beiden gegebenen Grammatiken und legt noch ein neues Startsymbol ${\text{S}}$ fest, das die ${\text{S}}_{1}{\text{-}}$ und ${\text{S}}_{2}$-Regeln vereint. Das Ergebnis ist in diesem Fall das folgende:

${\begin{aligned}&G:&&{\text{S}}\rightarrow {\text{aA}}_{1}\mid {\text{bB}}_{1}\mid {\text{a}}\mid {\text{bA}}_{2}\mid {\text{cA}}_{2}\\&&&{\text{S}}_{1}\rightarrow {\text{aA}}_{1}\mid {\text{bB}}_{1}\\&&&{\text{A}}_{1}\rightarrow {\text{aA}}_{1}\mid {\text{a}}\\&&&{\text{B}}_{1}\rightarrow {\text{bB}}_{1}\mid {\text{b}}\\&&&{\text{S}}_{2}\rightarrow {\text{a}}\mid {\text{bA}}_{2}\mid {\text{cA}}_{2}\\&&&{\text{A}}_{2}\rightarrow {\text{bA}}_{2}\mid {\text{cA}}_{2}\mid {\text{b}}\mid {\text{c}}\end{aligned}}$

Man kann hier die ${\text{S}}_{1}{\text{-}}$ und ${\text{S}}_{2}$-Regeln sogar wegstreichen, da ${\text{S}}_{1}$ und ${\text{S}}_{2}$ jetzt keine Startsymbole mehr sind und auf keiner rechten Seite erwähnt werden. In jedem Fall gilt jetzt $L(G)=L(G_{1})\cup L(G_{2}).$ In ähnlicher Weise kann man mit allen regulären Grammatiken verfahren. Die Klasse der regulären Sprachen ist unter Vereinigung abgeschlossen.

Wie sieht es mit der Konkatenation aus? Aus der Einschränkung für reguläre Grammatiken geht hervor, dass bei der Ableitung eines Wortes jede Satzform Element der Menge $\Sigma ^{\star }\cdot V$ ist. Es handelt sich also stets um eine Kette von Terminalen mit einem abschließenden Nichtterminal, da immer nur Regeln der Form ${\text{A}}\rightarrow {\text{aB}}$ angewendet werden. Nur im letzten Ableitungsschritt kommt eine Regel der Form ${\text{A}}\rightarrow {\text{a}}$ zur Anwendung. Danach sind keine Nichtterminale mehr vorhanden, die noch abgeleitet werden könnten. Anhand dieses Wissens, dass solche Regeln für die letzten Zeichen aller Wörter zuständig sind, kann man aus zwei Grammatiken $G_{1}$ und $G_{2}$ die Grammatik $G,$ für die $L(G)=L(G_{1})\cdot L(G_{2})$ gilt, erzeugen, indem man alle Produktionsregeln übernimmt und ${\text{A}}_{1}\rightarrow {\text{a}}$ in ${\text{A}}_{1}\rightarrow {\text{aS}}_{2}$ abändert. ${\text{S}}_{1}$ ist das Startsymbol der neuen Grammatik. Ein Beispiel sagt mehr als tausend Worte:

${\begin{aligned}&G_{1}:&&{\text{S}}_{1}\rightarrow {\text{aA}}_{1}\mid {\text{bB}}_{1}\\&&&{\text{A}}_{1}\rightarrow {\text{aA}}_{1}\mid {\text{a}}\\&&&{\text{B}}_{1}\rightarrow {\text{bB}}_{1}\mid {\text{b}}\\&G_{2}:&&{\text{S}}_{2}\rightarrow {\text{a}}\mid {\text{bA}}_{2}\mid {\text{cA}}_{2}\\&&&{\text{A}}_{2}\rightarrow {\text{bA}}_{2}\mid {\text{cA}}_{2}\mid {\text{b}}\mid {\text{c}}\\&G:&&{\text{S}}\rightarrow {\text{aA}}_{1}\mid {\text{bB}}_{1}\\&&&{\text{A}}_{1}\rightarrow {\text{aA}}_{1}\mid {\text{aS}}_{2}\\&&&{\text{B}}_{1}\rightarrow {\text{bB}}_{1}\mid {\text{bS}}_{2}\\&&&{\text{S}}_{2}\rightarrow {\text{a}}\mid {\text{bA}}_{2}\mid {\text{cA}}_{2}\\&&&{\text{A}}_{2}\rightarrow {\text{bA}}_{2}\mid {\text{cA}}_{2}\mid {\text{b}}\mid {\text{c}}\end{aligned}}$

Wenn man anhand der regulären Grammatik $G$ ein Wort ableitet, durchläuft man zuerst eine beliebige Folge von Nichtterminalen mit einer 1. Mit ${\text{S}}_{2}$ beginnt dann eine Folge von 2-Nichtterminalen, die mit einer Regel der Form ${\text{A}}_{2}\rightarrow {\text{a}}$ endet. Das Ergebnis ist eine Konkatenation eines Wortes aus $L(G_{1})$ mit einem aus $L(G_{2}).$ Die regulären Sprachen sind auch unter Konkatenation abgeschlossen.

Unter dem Kleene-Stern als Sonderfall der Konkatenation sind die regulären Sprachen demnach auch abgeschlossen. Man „konkateniert“ die Grammatik einfach mit sich selbst (In Wirklichkeit konkateniert man natürlich nicht die Grammatik, sondern man entwickelt eine Grammatik, die die Konkatenation der Sprache mit sich selbst erzeugt.), indem man für jede Regel ${\text{A}}\rightarrow {\text{a}}$ noch eine ${\text{A}}\rightarrow {\text{aS}}$ dazu gibt. Es ist dann möglich, bei der Ableitung Endlosschleifen zu durchlaufen, die immer wieder über das Startsymbol führen. Allerdings hat die Sache einen Haken: Das leere Wort $\varepsilon$ ist immer auch Element der Sprache $L^{\star }.$ Das heißt, es müsste eine Regel ${\text{S}}\rightarrow \varepsilon$ geben. Aber da nun ${\text{S}}$ in jedem Fall auch auf rechten Seiten auftaucht ${\text{(A}}\rightarrow {\text{aS),}}$ wird es hier nötig, ein wenig zu tricksen: Man benennt ${\text{S}}$ in ${\text{S}}_{0}$ um und führt ein neues Startsymbol ${\text{S}}$ ein, das alle ${\text{S}}_{0}{\text{-}}$Regeln übernimmt. Darüber hinaus kann es jetzt eine Regel ${\text{S}}\rightarrow \varepsilon$ geben, denn ${\text{S}}$ steht auf keiner rechten Seite, sondern nur ${\text{S}}_{0}{\text{.}}$ Es folgt wieder ein anschauliches Beispiel:

${\begin{aligned}&G:&&{\text{S}}\rightarrow {\text{aA}}\mid {\text{bB}}\\&&&{\text{A}}\rightarrow {\text{aA}}\mid {\text{a}}\\&&&{\text{B}}\rightarrow {\text{bB}}\mid {\text{b}}\\&G':&&{\text{S}}\rightarrow \varepsilon \mid {\text{aA}}\mid {\text{bB}}\\&&&{\text{S}}_{0}\rightarrow {\text{aA}}\mid {\text{bB}}\\&&&{\text{A}}\rightarrow {\text{aA}}\mid {\text{a}}\mid {\text{aS}}_{0}\\&&&{\text{B}}\rightarrow {\text{bB}}\mid {\text{b}}\mid {\text{bS}}_{0}\end{aligned}}$

$G'$ ist eine reguläre Grammatik – ${\text{S}}\rightarrow \varepsilon$ lässt man, wie gesagt, durchgehen – und es gilt $L(G')=(L(G))^{\star }.$ Die Klasse der regulären Sprachen ist unter Sternbildung abgeschlossen.

Ein weiterer Sonderfall der Konkatenation ist die Potenzierung. Möchte man eine reguläre Sprache $L(G)$ beispielsweise mit 2 potenzieren, dupliziert man $G$ und nennt das eine Exemplar $G_{1},$ wobei alle Nichtterminale den Index 1 tragen, und das andere $G_{2}.$ Dort haben alle Nichtterminale eine tiefgestellte 2. $G_{1}$ und $G_{2}$ sind immer noch reguläre Grammatiken und wie oben bereits gezeigt, ist auch $L(G_{1})\cdot L(G_{2})$ eine reguläre Sprache. Entsprechend kann man auf höhere Exponenten als 2 erweitern. Auch die Potenzierung regulärer Sprachen bringt also immer wieder reguläre Sprachen hervor.

Damit ist bewiesen, dass die regulären Sprachen unter Vereinigung, Konkatenation, Kleene-Stern und Potenzierung abgeschlossen sind. Das heißt, jeder Ausdruck wie dieser:
$\{0,1\}^{\star }\cdot \{1\}\cup \{0,1\}^{\star }\cdot \{1\}\cdot \{0,1\}$
beschreibt eine reguläre Sprache; und umgekehrt kann jede reguläre Sprache mit solch einem Ausdruck beschrieben werden. Man nennt diese Ausdrücke deshalb auch „reguläre Ausdrücke“. Reguläre Ausdrücke sind wegen ihrer Prägnanz eine echte Alternative zu ellenlangen Grammatiken. Normalerweise schreibt man sie sogar noch kürzer auf. Der obige reguläre Ausdruck ist äquivalent zu diesem hier:
$(0|1)^{\star }1|(0|1)^{\star }1(0|1)$
Die Konkatenationspunkte lässt man weg und die Vereinigungen werden mit senkrechten Strichen dargestellt. Wegen der dann wegfallenden geschweiften Klammern muss man eventuell zusätzliche Klammern einfügen.

Übung

Gib einen regulären Ausdruck für die Sprache über dem binären Alphabet an, deren Wörter als letztes oder vorletztes Zeichen eine 1 haben!

$(0|1)^{\star }1(0|)$

---

Gib einen regulären Ausdruck für die Sprache über dem binären Alphabet an, deren Wörter nicht das Teilwort „01“ enthalten!

$1^{\star }0^{\star }$

Tag 2

Zusammenfassung

Reguläre Sprachen können mit endlichen Automaten beschrieben werden, die das Wortproblem in linearer Zeit lösen. Ein deterministischer endlicher Automat besteht aus mehreren Zuständen, von denen einer ein Startzustand ist und beliebig viele Endzustände sind. Die Zustände sind über die möglichen Eingabezeichen miteinander verbunden. Ein DEA wird mit einem 5-Tupel $M=(S,\Sigma ,f,s_{0},F)$ charakterisiert.

Von den gestern besprochenen regulären Ausdrücken hast du vielleicht im Zusammenhang mit Algorithmen gehört, die aus Texten Zeichenfolgen heraussuchen. Fortgeschrittene Suchprogramme wie zum Beispiel  grep basieren auf regulären Ausdrücken. Der Benutzer gibt außer dem zu durchsuchenden Text einen regulären Ausdruck ein, der eine reguläre Sprache beschreibt. Die Wörter dieser Sprache sind die Zeichenfolgen, auf die der Algorithmus beim Durchsuchen des Textes anspringen soll. Wenn der Ausdruck zum Beispiel
$00101(0|1)^{\star }0110|(111|000)(0|1)^{\star }10011$
lautet, dann findet der Algorithmus aus dem Eingabetext die Folgen von Nullen und Einsen heraus, die vorne und hinten von „00101“ und „0110“, „111“ und „10011“ oder „000“ und „10011“ begrenzt werden. Der Algorithmus löst also das am Tag 3 in der 2. Woche (Grammatiken) angesprochene Wortproblem für alle Teilwörter des eingegebenen Textes.

Dass sich auf dem Gebiet der Suchalgorithmen die regulären Ausdrücke so hoher Beliebtheit erfreuen, hat natürlich seine Gründe: Das Wortproblem ist für reguläre Sprachen sehr effizient lösbar. Man kann für jede reguläre Sprache speicherschonende und schnell arbeitende Automaten entwickeln, die eine Zeichenkette einlesen und daraufhin ausgeben, ob das Wort zur Sprache gehört oder nicht. Diese Automaten sind zunächst theoretischer Natur, aber in ihrem Aufbau nicht allzu realitätsfern, so dass man sie auch in der Praxis einsetzen kann.

Ein Automat befindet sich zu jedem Zeitpunkt in einem bestimmten Zustand. Am Anfang ist das ein definierter Startzustand. Er liest dann ein Wort zeichenweise ein. Nach jedem gelesenen Zeichen wechselt er seinen Zustand in Abhängigkeit von diesem Zeichen. Einige der Zustände, die der Automat annehmen kann, werden als Endzustände bezeichnet. Wenn er sich, nachdem er alle Zeichen des Eingabewortes gelesen hat, in einem Endzustand befindet, ist das Wort Element der Sprache, die der Automat definiert; andernfalls nicht.

Es gibt eine verbreitete graphische Darstellungsform für solche Automaten:

Die Zustände werden als Kreise dargestellt. Wenn der Automat, unter der Voraussetzung, dass er sich im Zustand $a$ befindet, beim Lesen des Zeichens „0“ in den Zustand $b$ übergeht, dann zeichnet man vom Kreis mit dem $a$ zum Kreis mit dem $b$ einen Pfeil, der mit „0“ beschriftet ist. Außerdem wird der Startzustand mit einem unbeschrifteten Pfeil, der von keinem Zustand ausgeht, gekennzeichnet. In diesem Fall ist das der Zustand $s.$ Die Endzustände charakterisiert ein doppelter Kreis. Der Startzustand kann auch ein Endzustand sein. Dann gehört $\varepsilon$ auch zur Sprache. In diesem Fall trifft das aber nicht zu. Der oben dargestellte Automat erkennt die schon mehrfach beispielhaft verwendete Sprache über dem binären Alphabet, deren Wörter als letztes oder vorletztes Zeichen eine „1“ haben. Probiere es aus! Nimm dir ein Beispielwort, beginne bei $s$ und lasse dich von den Pfeilen leiten. Endet dein Weg bei einem Endzustand?

Wenn das zu überprüfende Wort „01101001“ lautet, dann sieht der Weg durch die Zustände so aus:
$\rightarrow s{\stackrel {0}{\rightarrow }}s{\stackrel {1}{\rightarrow }}a{\stackrel {1}{\rightarrow }}a{\stackrel {0}{\rightarrow }}b{\stackrel {1}{\rightarrow }}a{\stackrel {0}{\rightarrow }}b{\stackrel {0}{\rightarrow }}s{\stackrel {1}{\rightarrow }}a$
Da $a$ ein Endzustand ist, akzeptiert der Automat das Wort „01101001“ – es ist Element der Sprache.

Der hier beschriebene Typ von einem Automaten hat zwei Eigenschaften: Zum einen ist er endlich. Das heißt, er kann nur eine bestimmte Anzahl von Zuständen einnehmen. Zum Anderen ist er deterministisch. Dazu später mehr. Es reicht jetzt erstmal, zu wissen, dass es heute und morgen um deterministische endliche Automaten geht. Dieses Ungetüm von einem Begriff wird im Folgenden mit DEA abgekürzt.

Ein DEA wird ähnlich wie eine Grammatik mit einem 5-Tupel der folgenden Struktur definiert:
$M=(S,\Sigma ,f,s_{0},F)$
Dabei ist $S$ die Menge der Zustände, $\Sigma$ das Eingabealphabet, $f$ die Überführungsfunktion, $s_{0}$ der Startzustand und $F$ die Menge der Endzustände. Zur Erinnerung: Eine Grammatik ist ein 4-Tupel $G=(V,\Sigma ,P,{\text{S}}).$ Das sieht nicht nur ähnlich aus, das ist auch ähnlich. Sowohl eine Grammatik als auch ein Automat definiert eine Sprache.

Zu den einzelnen Gliedern des 5-Tupels Automat: $S$ als endliche Menge der möglichen Zustände ist in diesem Beispiel $\{s,a,b\}.$ Das Eingabealphabet ist $\Sigma =\{0,1\}.$ $F$ ist eine Teilmenge von $S:$ $F=\{a,b\}.$ Die Überführungsfunktion legt die Verdrahtung der Zustände untereinander fest. Sie erwartet zwei Parameter: Den aktuellen Zustand und das gerade anstehende Eingabezeichen. Der Rückgabewert der Funktion ist der Zustand, in den der Automat wechselt. Also es gilt $f(a,{\text{x}})=b,$ wenn beim Lesen des Zeichens „x“ ein Übergang vom Zustand $a$ zum Zustand $b$ stattfindet. Man kann auch mathematisch korrekt $f:S\times \Sigma \rightarrow S$ schreiben. (sprich: „$f$ ist definiert als $S$ Kreuz Sigma abgebildet auf $S.$“)

Den oben zeichnerisch dargestellten DEA kann man also auch in Textform eindeutig spezifizieren:

$M=(S,\Sigma ,f,s,F),S=\{s,a,b\},\Sigma =\{0,1\},F=\{a,b\}$
${\begin{aligned}&f(s,0)=s,&&f(s,1)=a,\\&f(a,0)=b,&&f(a,1)=a,\\&f(b,0)=s,&&f(b,1)=a\end{aligned}}$

Du kennst jetzt schon drei äquivalente Beschreibungsmöglichkeiten für reguläre Sprachen: reguläre Grammatiken, reguläre Ausdrücke und deterministische endliche Automaten. Es erwartet dich in dieser Woche noch eine weitere.

Übung

Entwirf einen DEA für den folgenden regulären Ausdruck sowohl zeichnerisch als auch formal.

$0(0|1)^{\star }$
Du kommst mit drei Zuständen aus. Davon ist einer ein Endzustand.

$M=(S,\Sigma ,f,s,F),S=\{s,a,b\},\Sigma =\{0,1\},F=\{b\}$

${\begin{aligned}&f(s,0)=b,&&f(s,1)=a,\\&f(a,0)=a,&&f(a,1)=a,\\&f(b,0)=b,&&f(b,1)=b\end{aligned}}$

Tag 3

Zusammenfassung

Da DEAs genau die reguläre Sprachen beschreiben, kann man zu jedem DEA eine äquivalente reguläre Grammatik finden.

Wer sagt eigentlich, dass die Sprachen, für die man DEAs entwickeln kann, genau die regulären Sprachen sind; nicht mehr und nicht weniger? Man kann es beweisen, indem man sich die Parallelen zwischen regulären Grammatiken und DEAs vor Augen führt.

Ein DEA, der gerade dabei ist, ein Wort abzuarbeiten, hat bereits eine gewisse Zeichenkette hinter sich gelassen und befindet sich in einem bestimmten Zustand. Diese Momentaufnahme kann man als Zwischenergebnis des DEA auffassen. Angenommen, dem Automaten wird der Saft abgedreht und er muss seine Arbeit abbrechen. Wenn er sich das Zwischenergebnis gemerkt hat, kann er später an dieser Stelle einsetzen und muss nicht ganz vorne anfangen. Aber das ist rein hypothetisch.

Setzt man den gestrigen Beispielautomaten auf das Wort „110100“ an, sieht die Folge der Zwischenergebnisse so aus:
$(\varepsilon ,s)\Rightarrow (1,a)\Rightarrow (11,a)\Rightarrow (110,b)\Rightarrow (1101,a)\Rightarrow (11010,b)\Rightarrow (110100,s)$
Das gleiche in vereinfachter Schreibweise ohne Klammern, Kommata und das Symbol $\varepsilon :$
${\text{S}}\Rightarrow {\text{1A}}\Rightarrow {\text{11A}}\Rightarrow {\text{110B}}\Rightarrow {\text{1101A}}\Rightarrow {\text{11010B}}\Rightarrow {\text{110100S}}$
Die Kleinbuchstaben der Zustände wurden klammheimlich durch Großbuchstaben, wie sie für Nichtterminale üblich sind, ersetzt, denn es handelt sich augenscheinlich um eine Folge von schrittweise abgeleiteten Satzformen auf der Grundlage der folgenden regulären Grammatik:

${\begin{aligned}&{\text{S}}\rightarrow {\text{1A}}\mid {\text{0S}}\mid {\text{1}}\\&{\text{A}}\rightarrow {\text{1A}}\mid {\text{0B}}\mid {\text{1}}\mid {\text{0}}\\&{\text{B}}\rightarrow {\text{1A}}\mid {\text{0S}}\mid {\text{1}}\end{aligned}}$

Wenn ein DEA ein Wort auf Gültigkeit überprüft, tut er also nichts anderes als dieses Wort anhand der regulären Grammatik abzuleiten, zu der er äquivalent ist. Wenn das Wort nicht Element der Sprache ist, dann bleibt in der letzten Satzform am Ende ein Nichtterminal stehen. Das Wort kann nicht abgeleitet werden. Abgeleitet werden kann ein Wort nur, wenn ganz zum Schluss eine Ableitungsregel der Form ${\text{A}}\rightarrow {\text{a}}$ angewendet und damit das letzte Nichtterminal ${\text{A}}$ eliminiert wird. Wenn man weiß, wie es geht, kann man also tatsächlich ohne größere geistige Anstrengung mit Zettel und Stift aus jedem DEA eine gleichwertige Grammatik erzeugen. Dazu geht man folgendermaßen vor:

• Das Alphabet $\Sigma$ der Grammatik ist das Alphabet $\Sigma$ des Automaten.
• Die Nichtterminalmenge $V$ der Grammatik ist die Zustandsmenge $S$ des Automaten. Es bietet sich an, die Variablen in Großbuchstaben zu benennen.
• Das Startsymbol ${\text{S}}$ der Grammatik ist der Startzustand $s_{0}$ des Automaten.
• Die Regelmenge $P$ der Grammatik enthält für alle möglichen Parameterkonstellationen der Überführungsfunktion $f$ des Automaten eine Produktionsregel. Dabei wird $f(z_{1},{\text{a}})=z_{2}$ zu ${\text{Z}}_{1}\rightarrow {\text{aZ}}_{2}.$
• Wenn $f(z_{1},{\text{a}})=z_{2}$ gilt und $z_{2}$ ein Endzustand ist, dann gehört zu $P$ außerdem die Regel ${\text{Z}}_{1}\rightarrow {\text{a}},$ denn es muss die Möglichkeit offengehalten werden, an dieser Regel die Ableitung zu beenden.

Wenn der Startzustand $s_{0}$ ein Endzustand ist und es die Möglichkeit gibt, nach dem Verlassen des Startzustandes wieder dorthin zurückzukehren, dann enthält $P$ sowohl die Regel ${\text{S}}\rightarrow \varepsilon$ als auch Regeln der Form ${\text{A}}\rightarrow {\text{aS.}}$ Es ist dann möglich, dass die Satzformen im Verlauf der Ableitung wieder kürzer werden, was ja der Voraussetzung für kontextsensitive Grammatiken widerspricht. Ein Nichtterminal, das zu $\varepsilon$ abgeleitet werden kann, darf auf keiner rechten Seite stehen. Deshalb muss in diesem Fall das Regelwerk der Grammatik noch folgendermaßen abgeändert werden:

• Das Startsymbol ${\text{S}}$ wird in ${\text{S}}_{0}$ umbenannt. Alle Regeln der Form ${\text{A}}\rightarrow {\text{aS}}$ werden in ${\text{A}}\rightarrow {\text{aS}}_{0}$ abgeändert.
• Die Regel ${\text{S}}_{0}\rightarrow \varepsilon$ wird entfernt.
• Es wird ein neues Symbol ${\text{S}}$ eingeführt, das alle Regeln von ${\text{S}}_{0}$ übernimmt.
• Die Regel ${\text{S}}\rightarrow \varepsilon$ wird eingeführt.

Nach dieser Bearbeitung der Grammatik beschreibt sie immer noch die gleiche reguläre Sprache, aber es kommen keine Nichtterminale, die zu $\varepsilon$ abgeleitet werden können, auf rechten Seiten vor.

Wenn man einen DEA hat, kann man also in jedem Fall eine entsprechende reguläre Grammatik finden. Natürlich funktioniert auch der umgekehrte Weg, der morgen thematisiert wird.

Übung

Entwickle eine reguläre Grammatik, die genau die gleiche Sprache beschreibt wie dieser DEA:

${\begin{aligned}&G=(V,\Sigma ,P,{\text{S}}),V=({\text{S, A, B}}),\Sigma =\{0,1\}\\&{\text{S}}\rightarrow {\text{1A}}\mid {\text{0B}}\mid {\text{0}}\\&{\text{A}}\rightarrow {\text{1A}}\mid {\text{0A}}\\&{\text{B}}\rightarrow {\text{1B}}\mid {\text{0B}}\mid {\text{1}}\mid {\text{0}}\end{aligned}}$

Man erhält oft nicht die optimale Grammatik, wenn man stur nach den beschriebenen Regeln vorgeht. Diese hier könnte man zum Beispiel noch reduzieren:
${\begin{aligned}&{\text{S}}\rightarrow {\text{0B}}\mid {\text{0}}\\&{\text{B}}\rightarrow {\text{1B}}\mid {\text{0B}}\mid {\text{1}}\mid {\text{0}}\end{aligned}}$
${\text{A}}$ kann nicht zu Terminalen abgeleitet werden. Deshalb tut dieses Symbol nichts zur Sache und kann weggelassen werden.

Tag 4

Zusammenfassung

Man kann zu jeder regulären Grammatik einen NEA und zu jedem NEA einen DEA entwickeln. Damit ist jetzt hinreichend bewiesen, dass endliche Automaten und reguläre Grammatiken äquivalent sind. NEAs können mehrere Startzustände, beliebig viele Zustandsübergänge für jedes Eingabezeichen und Sackgassen haben.

Wenn man beweisen will, dass DEAs und reguläre Grammatiken die gleiche Sprachklasse abdecken (nämlich die der regulären Sprachen), muss man jetzt nur noch zeigen, dass man zu jeder regulären Grammatik auch einen DEA finden kann. Zunächst braucht man für den zu entwerfenden Automaten so viele Zustände (also Kreise) wie die Grammatik Nichtterminale hat, und noch einen zusätzlich, der hier $e$ genannt werden soll. Man sollte wieder die Großbuchstaben durch Kleinbuchstaben ersetzen. Der Startzustand, der dem Startsymbol der Grammatik entspricht, erhält einen Pfeil, um ihn als Startzustand zu markieren. Wenn es die Produktionsregel ${\text{S}}\rightarrow \varepsilon$ gibt, ist der Startzustand auch ein Endzustand. Er bekommt einen doppelten Kreis. Der Zustand $e$ ist außerdem in jedem Fall Endzustand; daher das $e.$ Dann wird für jede Regel nach dem Muster ${\text{A}}\rightarrow {\text{cB}}$ ein Pfeil von $a$ nach $b$ gezeichnet, der mit „c“ beschriftet ist. Und für jede Regel ${\text{A}}\rightarrow {\text{b}}$ wird ein mit „b“ beschrifteter Pfeil von $a$ nach $e$ gezeichnet. Damit ist sichergestellt, dass man nach diesem Zeichen die Ableitung bzw. den Weg durch den Automaten beenden kann, denn $e$ ist ein Endzustand.

Probieren wir das an dieser Grammatik aus:

${\begin{aligned}&{\text{S}}\rightarrow \varepsilon \mid {\text{1A}}\mid {\text{1B}}\mid {\text{0B}}\\&{\text{A}}\rightarrow {\text{1}}\mid {\text{0}}\mid {\text{1A}}\mid {\text{1B}}\mid {\text{0B}}\\&{\text{B}}\rightarrow {\text{0}}\mid {\text{0B}}\end{aligned}}$

Die Sprache, die diese Grammatik beschreibt, umfasst alle Folgen von Nullen und Einsen, die nicht das Teilwort „01“ enthalten (außer „0“ und „1“). Wendet man die oben genannten Richtlinien an, ergibt das den folgenden Automaten:

Das ist, zugegebenermaßen, ein ziemlich seltsamer Automat. Wenn das erste Zeichen eine „1“ ist, soll man dann von $s$ auf $a$ oder auf $b$ übergehen? Und wenn der Automat sich im Zustand $b$ befindet und es kommt eine „0“ als Eingabezeichen, bleibt er dann auf $b$ oder wechselt er auf $e{\text{?}}$ Und wenn statt einer „0“ eine „1“ kommt, dann gibt es gar keinen Ausweg mehr.

Es handelt sich um einen nichtdeterministischen endlichen Automaten, einen NEA. Es kann für ein Eingabezeichen mehrere mögliche Zustandsübergänge geben. Es kann auch sein, dass gar kein Pfeil existiert, der mit einem bestimmten Zeichen beschriftet ist. Wenn solch ein NEA nun eine Eingabe erhält, sucht er sich nicht nach Gutdünken einen Pfad durch seine Zustände aus, sondern eigentlich muss er alle Möglichkeiten ausprobieren. Wenn die Eingabe zum Beispiel „1100“ lautet, gibt es folgende sechs Wege durch die Zustände:

${\begin{aligned}&\rightarrow s{\stackrel {1}{\rightarrow }}a{\stackrel {1}{\rightarrow }}a{\stackrel {0}{\rightarrow }}b{\stackrel {0}{\rightarrow }}b,\\&\rightarrow s{\stackrel {1}{\rightarrow }}a{\stackrel {1}{\rightarrow }}a{\stackrel {0}{\rightarrow }}b{\stackrel {0}{\rightarrow }}e,\\&\rightarrow s{\stackrel {1}{\rightarrow }}a{\stackrel {1}{\rightarrow }}a{\stackrel {0}{\rightarrow }}e{\stackrel {0}{\rightarrow }}{\text{(Sackgasse),}}\\&\rightarrow s{\stackrel {1}{\rightarrow }}a{\stackrel {1}{\rightarrow }}e{\stackrel {0}{\rightarrow }}{\text{(Sackgasse),}}\\&\rightarrow s{\stackrel {1}{\rightarrow }}b{\stackrel {1}{\rightarrow }}{\text{(Sackgasse) und}}\\&\rightarrow s{\stackrel {1}{\rightarrow }}e{\stackrel {1}{\rightarrow }}{\text{(Sackgasse)}}\end{aligned}}$

Vier Wege enden in einer Sackgasse. Einer endet in einem Zustand, der kein Endzustand ist. Aber es ist auch ein Weg darunter, der in einem Endzustand endet. Deshalb akzeptiert der Automat das Wort „1100“. Es reicht aus, wenn es nur eine Möglichkeit gibt, die Zustandsübergänge so anzuordnen, dass am Ende ein Endzustand steht.

Leider lassen sich NEAs nicht so effizient algorithmisch umsetzen wie DEAs, denn Algorithmen, in denen Floskeln wie „alle Varianten durchprobieren“ vorkommen, sind meistens nicht besonders vorteilhaft. Und eigentlich sollte es heute ja darum gehen, zu zeigen, dass jede reguläre Grammatik auch als DEA und nicht als NEA dargestellt werden kann. Glücklicherweise lassen sich beide Probleme recht schnell lösen, denn zu jedem NEA kann man einen entsprechenden DEA finden.

Dazu zuerst ein paar Formalien: Sowohl ein DEA als auch ein NEA ist ein 5-Tupel $M=(S,\Sigma ,f,s_{0},F)$ mit der Zustandsmenge, dem Alphabet, der Überführungsfunktion, dem Startzustand und der Endzustandsmenge in dieser Reihenfolge. Der einzige Unterschied zwischen den beiden Konzepten liegt in der Überführungsfunktion: Das Ergebnis der Überführungsfunktion $f$ ist beim NEA nicht ein Zustand, sondern eine Menge von Zuständen, in die der Automat übergehen kann. Diese Menge kann natürlich eventuell auch nur ein Element haben. Sie kann auch leer sein.

Der oben aufgezeichnete NEA sieht als mathematische Definition so aus:

$M=(S,\Sigma ,f,s_{0},F),S=\{s,a,b,e\},\Sigma =\{0,1\},s_{0}=s,F=\{s,e\}$
${\begin{aligned}&f(s,0)=\{b\},&&f(s,1)=\{a,b\}\\&f(a,0)=\{b,e\},&&f(a,1)=\{a,b,e\}\\&f(b,0)=\{b,e\},&&f(b,1)=\emptyset \\&f(e,0)=\emptyset ,&&f(e,1)=\emptyset \end{aligned}}$

Dieser NEA soll nun als DEA dargestellt werden. Nimmt man an, dass der NEA, der auf ein Eingabewort angesetzt wird, die möglichen Abfolgen von Zuständen nicht nacheinander, sondern gleichzeitig durchprobiert, dann befindet er sich zu jedem Zeitpunkt in einer gewissen Menge von Zuständen. Diese Vorstellung ist jetzt ziemlich wirklichkeitsfern, wie auch das ganze Konzept NEA unrealistisch ist. Aber es naht Rettung: Wenn man diese Menge von Zuständen, in denen sich der Automat in einem gewissen Moment gleichzeitig befindet, als Einheit betrachtet, kann man sie auch als einzelnen Zustand auffassen. Ein NEA mit den drei Zuständen $a,b$ und $c,$ der sich gerade in den Zuständen $a$ und $b$ befindet, ist also nichts weiter als ein DEA mit den acht Zuständen $\emptyset ,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\}$ und $\{a,b,c\},$ der sich gerade im Zustand $\{a,b\}$ befindet.

Hat der NEA das gesamte Wort abgearbeitet, befindet er sich wieder in einer Anzahl von Zuständen. Ist unter diesen Zuständen wenigstens ein Endzustand, dann gilt das Wort als akzeptiert. Sei also zum Beispiel $b$ ein Endzustand des NEA. Dann hat der entsprechende DEA die Endzustände $\{b\},\{a,b\},\{b,c\}$ und $\{a,b,c\}.$ Auf diese Weise kann man jedem x-beliebigen NEA einen DEA zuordnen, der die gleiche reguläre Sprache beschreibt. Reguläre Grammatiken, DEAs und NEAs sind äquivalent. Man sagt deshalb auch ganz allgemein, dass reguläre Sprachen genau die Sprachen sind, die von endlichen Automaten erkannt werden.

Wandelt man den Beispiel-NEA für die Sprache, deren Wörter „01“ nicht enthalten, nach der beschriebenen Vorgehensweise in einen DEA um, ergibt sich das folgende Bild:

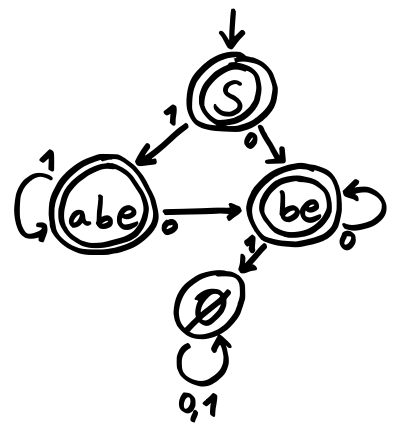
Die Zustände, die vom Startzustand aus nicht erreichbar sind, wurden hier gleich weggelassen.

Wenn der NEA sich im Zustand $s$ befindet und eine „1“ eingegeben wird, ist ein Übergang nach $a,b$ oder $e$ möglich. Aus diesem Grunde geht der DEA hier in jedem Fall in den Zustand $\{a,b,e\}$ über, welcher wegen $e$ ein Endzustand ist. Nach der Eingabe „0“ lautet der nächste Zustand $\{b,e\},$ denn im NEA gibt es von $a$ aus einen Übergang nach $b$ und $e,$ von $b$ aus ebenfalls nach $b$ und $e$ und von $e$ aus gibt es keinen Übergang. Alle Zielzustände zusammengenommen ergeben $\{b,e\}.$ Da der NEA weder für $b,$ noch für $e$ einen Übergang definiert, der mit „1“ beschriftet ist, geht der DEA, der sich in $\{b,e\}$ befindet, bei der Eingabe einer „1“ in den Zustand über, der mit dem Zeichen für die leere Menge beschriftet ist. Ein DEA darf keine Sackgassen haben. Deshalb zeigt $\emptyset$ für alle Eingaben auf sich selbst.

Übung

Ist das ein deterministischer oder ein nichtdeterministischer endlicher Automat?

Der Automat wurde als deterministischer vorgestellt. Aber jeder deterministische Automat ist auch ein nichtdeterministischer. Die Richtlinien beim Entwerfen von NEAs sind lockerer. Trotzdem kann man mit NEAs aber nicht mehr Sprachen beschreiben als mit DEAs.

Tag 5

Zusammenfassung

Äquivalenzklassen sind Mengen von Wörtern, die einen Automaten in den gleichen Zustand überführen. Anhand einer Überlegung über Äquivalenzklassen kann man Minimalautomaten erzeugen. Es gibt einen Algorithmus, um einen DEA darauf zu testen, ob er mehr Zustände hat, als er eigentlich bräuchte, um die jeweilige Sprache zu beschreiben.

Gestern wurde eine reguläre Grammatik über dem Umweg eines NEA in einen DEA umgewandelt. Jetzt stellt sich doch die Frage, ob dieser Automat minimal ist; also ob er bereits die kleinstmögliche Anzahl an Zuständen hat. Vielleicht ist es ja möglich, einen DEA mit weniger als vier Zuständen zu finden, der trotzdem die gleiche Sprache akzeptiert.

Dazu folgende Überlegung: Wenn der abgebildete Automat die Eingabe „11000“ erhält, befindet er sich im Zustand $be.$ Gibt man stattdessen „0“ ein, befindet er sich ebenfalls im Zustand $be.$ Da der Automat über keinen Speicher verfügt, hat er keine Möglichkeit, zurückzublicken. Er weiß nicht, welche Zeichenkette er bereits verarbeitet hat. Er sieht nur seinen aktuellen Zustand. Aus diesem Grunde kann man jetzt ohne weiteres Nachdenken feststellen, dass die Eingaben „110001010“ und „01010“ den Automaten letztendlich in den selben Zustand überführen; denn „11000“ und „0“ sind äquivalent und alles, was danach kommt, ist bei beiden Eingaben gleich. Man sagt, „11000“ und „0“ sind Elemente der Äquivalenzklasse $[0].$ Diese Äquivalenzklasse ist die Menge von Wörtern, die auf den Zustand $be$ führen.
$[0]=\{0,10,100,1100,11000,\ldots \}$
Man kann für jeden Zustand genau eine Äquivalenzklasse finden. Es gibt also insgesamt vier Äquivalenzklassen: $[\varepsilon ],[0],[1]$ und $[01].$

Es ist nun zu entscheiden, ob man zwei Äquivalenzklassen zusammenfassen kann; also ob alle Wörter aus der Äquivalenzklasse $a$ auch äquivalent zu allen Wörtern aus $b$ sind. Die Frage, ob man zwei Äquivalenzklassen zusammenfassen kann, ist schwer zu greifen. Gehen wir stattdessen andersherum vor: Welche je zwei Äquivalenzklassen kann man in jedem Fall nicht zusammenfassen? Man braucht also eine Tabelle:

	$[\varepsilon ]$	$[0]$	$[1]$
$[0]$
$[1]$
$[01]$

Die Paare, von denen eine Äquivalenzklasse einem Endzustand entspricht, also Wörter enthält, die Elemente der Sprache sind, und die andere nicht, sind schon mal unvereinbar. Von den vier Wörtern $\varepsilon ,$ „0“, „1“ und „01“ ist „01“ das einzige, das der Definition der Sprache widerspricht. Also markiert man in der Tabelle $[01]/[\varepsilon ],$ $[01]/[0]$ und $[01]/[1]$ – das sind alles paarweise verschiedene Äquivalenzklassen.

	$[\varepsilon ]$	$[0]$	$[1]$
$[0]$
$[1]$
$[01]$	$\star$	$\star$	$\star$

Kann man vielleicht $[0]$ und $[1]$ zusammenfassen? Wenn ja, dann müssten nicht nur „0“ und „1“, sondern auch „01“ und „11“ äquivalent sein, also $[01]$ und $[11]$ die selbe Äquivalenzklasse sein. Aber laut Automat gilt $[11]=[1]$ und $[01]$ ist nicht vereinbar mit $[1],$ da $[01]/[1]$ in der Tabelle markiert ist. Also ist $[0]/[1]$ auch nicht vereinbar und wird markiert.

	$[\varepsilon ]$	$[0]$	$[1]$
$[0]$			$\star$
$[1]$		$\star$
$[01]$	$\star$	$\star$	$\star$

Verlängert man ein Wort aus $[\varepsilon ]$ um „0“, erhält man ein Wort aus $[0].$ Verlängert man ein Wort aus $[0]$ um „0“, erhält man ebenfalls ein Wort aus $[0].$ Möglicherweise kann man $[\varepsilon ]$ und $[0]$ verschmelzen? Aber $[\varepsilon ]$ um „1“ verlängert ergibt $[1]$ und $[0]$ um „1“ verlängert ergibt $[01].$ Das Paar $[0]/[01]$ ist markiert, also muss auch $[\varepsilon ]/[0]$ markiert werden.

	$[\varepsilon ]$	$[0]$	$[1]$
$[0]$	$\star$		$\star$
$[1]$		$\star$
$[01]$	$\star$	$\star$	$\star$

Jetzt fehlt nur noch $[\varepsilon ]/[1].$ Hängt man „0“ an beide hinten ran, ergibt sich das logischerweise unmarkierte $[0]/[0].$ Bei „1“ erhält man das ebenfalls unmarkierte $[1]/[1].$ $[\varepsilon ]/[1]$ darf also nicht markiert werden. Es ist das einzige Paar Äquivalenzklassen, das zu einer verschmolzen werden kann. Man erhält also den folgenden Äquivalenzklassenautomaten, der zugleich der minimale DEA ist:

Zusammenfassend: Will man von einem DEA feststellen, ob er minimal ist, muss man fragen, welche Zustände äquivalent sind; und zwar über den Umweg der Frage nach den Zuständen oder Äquivalenzklassen, die nicht äquivalent sind.

Übung

Stelle fest, ob dieser DEA minimal ist und gib gegebenenfalls den Minimalautomaten an!

Die Zustände $a/c$ und $b/d$ können jeweils verschmolzen werden. Es ergibt sich der folgende Minimalautomat:

Rückblick

Lies dir heute die Zusammenfassungen noch einmal durch. Wenn du sehr viel Zeit und Lust hast, kannst du natürlich auch alles lesen. Gehe kurz die Übungen der vergangenen Tage durch und versuche dich dann an diesen:

Übung

Entwickle zu dieser Grammatik einen NEA:

${\begin{aligned}&{\text{S}}\rightarrow \varepsilon \mid {\text{0A}}\mid {\text{1B}}\mid {\text{0}}\mid {\text{1}}\\&{\text{A}}\rightarrow {\text{0A}}\mid {\text{1B}}\mid {\text{0}}\mid {\text{1}}\\&{\text{B}}\rightarrow {\text{0C}}\mid {\text{1B}}\mid {\text{0}}\mid {\text{1}}\\&{\text{C}}\rightarrow {\text{0A}}\mid {\text{0}}\end{aligned}}$

$M=(S,\Sigma ,f,s_{0},F),S=\{s,a,b,c,e\},\Sigma =\{0,1\},s_{0}=s,F=\{s,e\}$
${\begin{aligned}&f(s,0)=\{a,e\},&&f(s,1)=\{b,e\}\\&f(a,0)=\{a,e\},&&f(a,1)=\{b,e\}\\&f(b,0)=\{c,e\},&&f(b,1)=\{b,e\}\\&f(c,0)=\{a,e\},&&f(c,1)=\emptyset \\&f(e,0)=\emptyset ,&&f(e,1)=\emptyset \end{aligned}}$

---

Entwickle zu dem NEA aus der oben stehenden Übung einen DEA.

$M=(S,\Sigma ,f,s_{0},F),S=\{s,ae,be,ce,\emptyset \},\Sigma =\{0,1\},s_{0}=s,F=\{s,ae,be,ce\}$
${\begin{aligned}&f(s,0)=ae,&&f(s,1)=be\\&f(ae,0)=ae,&&f(ae,1)=be\\&f(be,0)=ce,&&f(be,1)=be\\&f(ce,0)=ae,&&f(ce,1)=\emptyset \\&f(\emptyset ,0)=\emptyset ,&&f(\emptyset ,1)=\emptyset \end{aligned}}$

---

Überprüfe, ob der DEA aus der oben stehenden Übung minimal ist. Wenn nicht, entwickle dazu einen Minimalautomaten.

Da die Zustände $\{s\}$ und $\{a,e\}$ sowohl für die Eingabe „0“ als auch für „1“ jeweils auf den selben Zustand zeigen und beide Endzustände sind, können diese zu einem reduziert werden.

$M=(S,\Sigma ,f,s_{0},F),S=\{sae,be,ce,\emptyset \},\Sigma =\{0,1\},s_{0}=sae,F=\{sae,be,ce\}$
${\begin{aligned}&f(sae,0)=sae,&&f(sae,1)=be\\&f(be,0)=ce,&&f(be,1)=be\\&f(ce,0)=sae,&&f(ce,1)=\emptyset \\&f(\emptyset ,0)=\emptyset ,&&f(\emptyset ,1)=\emptyset \end{aligned}}$

---

Wie lässt sich die Sprache, um die es in den oben stehenden Übungen geht, als regulärer Ausdruck darstellen?

$(0^{\star }1^{\star }100)^{\star }0^{\star }1^{\star }(|0)$

In diesem Rückblick ging es um die Sprache über dem binären Alphabet, deren Wörter das Teilwort „101“ nicht enthalten. Der Aufbau dieses regulären Ausdrucks lässt sich folgendermaßen erklären: $(0^{\star }1^{\star })^{\star }$ ist gleichbedeutend mit $(0|1)^{\star }:$ alle Folgen von Nullen und Einsen, einschließlich $\varepsilon .$ $1^{\star }1$ ist eine beliebige Folge von Einsen, die allerdings mindestens die Länge 1 hat. $(0^{\star }1^{\star }100)^{\star }$ ist also eine Folge von Nullen und Einsen, wobei nach jeder Folge von Einsen nicht nur eine Null stehen darf. Es müssen mindestens zwei sein. $(0^{\star }1^{\star }100)^{\star }$ bedeutet aber auch, dass jedes Wort außer $\varepsilon$ mit der Zeichenfolge „100“ enden muss. Da es auch andere mögliche Enden gibt, folgt $0^{\star }1^{\star }.$ Damit sind fast alle Enden abgedeckt. Aber nur fast. Es fehlt noch die Möglichkeit, das Wort mit „10“ abzuschließen. Deshalb wird noch die Option, nichts oder eine „0“ an das Wort zu konkatenieren, angefügt.