Irrlicht - from Noob to Pro: 2D-Bilder rotieren

Zurück zu "2D-Animationen" | Hoch zu "Inhaltsverzeichnis" | Vor zu XML in Irrlicht"

Allgemeines

Irrlicht bietet leider keine integrierte Methode ein Bild zu rotieren. Es gibt aber Möglichkeiten genau das per Hand vorzunehmen. Wir werden uns kurz vorher die Mathematik dazu anschauen und eine Funktion entwickeln, die Bilder rotieren kann. Mithilfe dieser werden wir folgendes Bild um 90° rotieren.

Die mathematische Sicht

Auch wenn das Kapitel relativ mathematiklastig ist kommen wir nicht drumherum uns die zu grundeligenden Gedanken anzuschauen. Dabei gliedern wir dies in 2 Teile.

Rotationsmatrix

Wir werden uns hier keine ausgedehnte Herleitung anschauen, sondern vielmehr Dinge als gegeben annehmen. Wer sich nähar dafür interessiert ist hiermit auf [Wikipedia] verwiesen. Die Rotationsmatrix R rotiert einen Punkt P um einen bestimmten Winkel φ. Demnach erhalten wir den Punkt P' indem wir R mit P multiplizieren. Wem die Matrizenschreibweise nicht geläufig ist der kann sich nun das ganze ausgeschrieben betrachten.

x' = x*cos(φ) - y*sin(φ)
y' = x*sin(φ) + y*cos(φ)

Zu beachten hierbei ist, dass es sich um eine Rotation um den Koordinatenursprung handelt. Da Irrlicht beim Rendern eines Bildes die linke obere Ecke als Ursprung nimmt, würden wir auch um diesen rotieren. Bei einer Rotation um 90° würde das aber bedeuten, dass das neu entstehende Bild direkt links neben dem Originalbild dargestellt wird und somit nichts angezeigt wird. Daher müssen wir um den Bildmittelpunkt rotieren!

Rotation um einen Punkt

Nun wollen wir einen Punkt P um einen anderen Punkt K mit dem Winkel φ rotieren. Nachfolgende Grafik soll dies veranschaulichen.

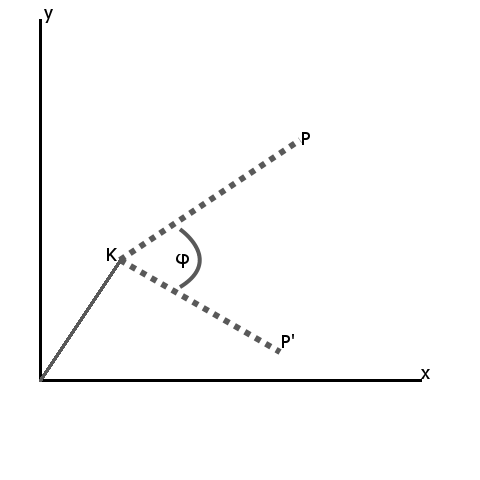
Dabei können wir uns die Überlegungen von zuvor als Grundlage nehmen. Denn was wir brauchen ist nichts weiter als eine Rotation um den Ursprung, nur dass jetzt K unser Ursprung ist. Wir müssen also K in unseren Ursprung legen, die Rotation ausführen und wieder um K verschieben. Somit erhalten wir unseren Punkt P' durch

x' = (x-kx)*cos(φ) - (y-ky)*sin(φ) + kx
y' = (x-kx)*sin(φ) + (y-ky)*cos(φ) + ky

Die Rotationsfunktion

Nun haben wir die letztendliche Rotationsfunktion in der Hand und müssen dies nur noch auf Irrlicht übersetzen. Wir werden nun ein Bild Pixel für Pixel rotieren, indem wir die gefundene Rotationsfunktion darauf anwenden. Wir benutzen die Klasse IImage da wir da Zugriff auf alle Pixel haben und diese auch manipulieren können.

ITexture* rotateImage(ITexture* source, f32 angle)
{
	//Bild nicht gültig -> Abbruch
	if(!source)
	{
		return NULL;
	}

	//Keine Rotation -> gib Originalbild zurück
	if(angle == 0.0f)
	{
		return source;
	}

	IVideoDriver* driver = device->getVideoDriver();

	//Rotationsmittelpunkt = Bildmittelpunkt
	s32 midx = source->getOriginalSize().Width/2;
	s32 midy = source->getOriginalSize().Height/2;

	//erstelle virtuelles Bild vom Original
	IImage* virtualSourceImage = driver->createImage(source, position2d<s32>(0,0), source->getOriginalSize());
	
	//erstelle unser Zielbild
	//dies hat die Größe vom weitentferntesten Punkt!
	IImage* target = driver->createImage(ECF_A8R8G8B8, dimension2d<u32>(2*sqrt((f32)(midx*midx + midy*midy)), 2*sqrt((f32)(midx*midx + midy*midy))));
	target->fill(SColor(0,0,0,0));

	s32 tx = 0, ty = 0;

	//rotiere alle Pixel mit der Rotationsmatrix
	for(s32 x = 0; x < (s32) source->getOriginalSize().Width; x++)
	{
		for(s32 y = 0; y < (s32) source->getOriginalSize().Height; y++)
		{
			tx = (s32)((x-midx)*cos(angle*3.14159265/180) - (y-midy)*sin(angle*3.14159265/180));
			ty = (s32)((y-midy)*cos(angle*3.14159265/180) + (x-midx)*sin(angle*3.14159265/180));

			target->setPixel(tx+midx,ty+midy, virtualSourceImage->getPixel(x,y));
		}
	}

	//gib Bild zurück
	return driver->addTexture("rotatedImage", target);	
}

Was auffallen sollte, ist die Dimensionsangabe beim erstellen des Zielbildes. Da wir das Bild rotieren vertauschen sich Beispielsweise bei einer 90° Drehung die Höhe und Breite des Bildes, sofern diese nicht zufällig gleich groß sind. Wenn wir die gleiche Dimension wie beim Originalbild annehmen, würde also Das Bild beschnitten werden. Um dem vorzubeugen ist unsere neue Größe gleich der Diagonalen des gesamten Bildes, da dessen komplette Rotation einen Kreis beschreibt, in dem alle restlichen Pixel enthalten sind und wir somit sichergehen, dass wir auch das komplette gedrehte Bild am Ende sehen werden.

Mathematikfunktionen in C++ gehen von Winkeln im Radiantenmaß aus. Da wir aber Gradangaben (Deg) benutzen, müssen wir eine Umwandlung von Rad in Deg vornehmen. Diese wäre:
deg = rad*180/PI;

Und schon haben wir unsere Rotationsfunktion geschrieben, die jedes beliebige Bild in Irrlicht um einen beliebigen Winkel rotieren kann. Und so sieht das Resultat des unten aufgeführten Programmes aus:

#include <irrlicht.h>

#pragma comment(lib, "Irrlicht.lib")

using namespace irr;

using namespace core;
using namespace scene;
using namespace video;
using namespace gui;
using namespace io;


IrrlichtDevice* device;

ITexture* rotateImage(ITexture* source, f32 angle)
{
	//Bild nicht gültig -> Abbruch
	if(!source)
	{
		return NULL;
	}

	//Keine Rotation -> gib Originalbild zurück
	if(angle == 0.0f)
	{
		return source;
	}

	IVideoDriver* driver = device->getVideoDriver();

	//Rotationsmittelpunkt = Bildmittelpunkt
	s32 midx = source->getOriginalSize().Width/2;
	s32 midy = source->getOriginalSize().Height/2;

	//erstelle virtuelles Bild vom Original
	IImage* virtualSourceImage = driver->createImage(source, position2d<s32>(0,0), source->getOriginalSize());
	
	//erstelle unser Zielbild
	//dies hat die Größe vom weitentferntesten Punkt!
	IImage* target = driver->createImage(ECF_A8R8G8B8, dimension2d<u32>(2*sqrt((f32)(midx*midx + midy*midy)), 2*sqrt((f32)(midx*midx + midy*midy))));
	target->fill(SColor(0,0,0,0));

	s32 tx = 0, ty = 0;

	//rotiere alle Pixel mit der Rotationsmatrix
	for(s32 x = 0; x < (s32) source->getOriginalSize().Width; x++)
	{
		for(s32 y = 0; y < (s32) source->getOriginalSize().Height; y++)
		{
			tx = (s32)((x-midx)*cos(angle*3.14159265/180) - (y-midy)*sin(angle*3.14159265/180));
			ty = (s32)((y-midy)*cos(angle*3.14159265/180) + (x-midx)*sin(angle*3.14159265/180));

			target->setPixel(tx+midx,ty+midy, virtualSourceImage->getPixel(x,y));
		}
	}

	//gib Bild zurück
	return driver->addTexture("rotatedImage", target);	
}

int main(int argc, char **argv)
{
	device = createDevice(EDT_OPENGL, dimension2d<u32>(640,480));
	
	if(device)
	{
		IVideoDriver* driver = device->getVideoDriver();
		IGUIEnvironment* guidev = device->getGUIEnvironment();
	
		ITexture* anImage = driver->getTexture("avatar.png");
		ITexture* rotatedImage = rotateImage(anImage, 90.0f);

		while(device->run())
		{
			driver->beginScene(true,true, SColor(255,255,255,255));
				driver->draw2DImage(rotatedImage, position2d<s32>(0,0), rect<s32>(position2d<s32>(0,0), rotatedImage->getOriginalSize()), 0, SColor(255,255,255,255), true);
			driver->endScene();
		}
		
		device->drop();
	}	

	return 0;
}