Statistik: Konzentration
Die Konzentration befasst sich mit der Intensität, mit der sich ein Objekt auf eine vorgegebene Menge verteilt. Eine typische Aussage der Konzentrationsmessung wäre etwa: 20% der Menschen eines bestimmten Staates besitzen 90% des Vermögens. Demnach teilen sich die anderen 80% die restlichen 10%. Hier kann man von einer starken Konzentration sprechen.
Kino-Beispiel
Im Rahmen einer Controllinganalyse eines Kinos wurden die Besucherzahlen (Merkmal x) für die 5 angebotenen Spielfilme an einem Tag erfasst. Man erhielt die Tabelle
| Filmtitel | Zahl der Besucher x |
|---|---|
| Rotkäppchen | 25 |
| Verliebt ins Abendrot | 75 |
| Leif Erikson | 125 |
| Söhne der Alhambra | 250 |
| Galaxy-Fighter | 525 |
Definitionen
Es gibt verschiedene Verfahren zur Konzentrationsmessung. Man kann die Konzentration grafisch darstellen oder Kennwerte berechnen. Die Merkmalsbeträge x müssen aufsteigend geordnet vorliegen, also .
Für die Konzentrationsmessung werden neben der relativen Summenfunktion Si* folgende Definitionen benötigt:
- Merkmalssumme
- Kumulierte Merkmalsbeträge
- Relative kumulierte Merkmalsbeträge
Grafik
Die Lorenzkurve ist eine grafische Darstellung der Konzentration:
Die Wertepaare (Si*;qi*) werden in einem Diagramm abgetragen. Das erste Wertepaar ist (0;0), das letzte (1;1). Es wird zwischen diesen beiden Wertepaaren die Winkelhalbierende des Koordinatensystems eingetragen. Alle Wertepaare (0;0), (S1*;q1*), ... , (1;1) werden geradlinig verbunden.
Tabelle
Die für die Lorenzkurve benötigten Zwischenwerte werde in der folgenden Tabelle aufgeführt. So ergibt sich beispielsweise für die kumulierten Merkmalsbeträge qi
- , , usw.
Die relativen oder anteiligen Merkmalsbeträge errechnen sich durch Teilen des Gesamtmerkmalbetrags 1000, also
- usw.
Ebenso ermitteln wir die absolute Summenhäufigkeiten als Zahl der Filme, also
- , , ...
und wiederum die relative Summenhäufigkeit mit
- , , ...
Es wurde außerdem noch als Platzhalter die Zeile für i = 0 eingefügt.
|
i |
Filmtitel |
xi |
qi |
qi* |
Si |
Si* |
|---|---|---|---|---|---|---|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
Rotkäppchen |
25 |
25 |
0,025 |
1 |
0,2 |
|
2 |
Verliebt ins Abendrot |
75 |
100 |
0,100 |
2 |
0,4 |
|
3 |
Leif Erikson |
125 |
225 |
0,225 |
3 |
0,6 |
|
4 |
Söhne der Alhambra |
250 |
475 |
0,475 |
4 |
0,8 |
|
5 |
Galaxy-Fighter |
525 |
1000 |
1,000 |
5 |
1 |
|
Summe |
|
1000 |
|
|
|
|
So wurden beispielsweise 40% (S2*) der Filme von nur 10% (q2*) der Besucher angesehen.
Die Lorenzkurve ist eine grafisches Maß für das Ausmaß einer Konzentration. Je weiter die Kurve „durchhängt“, desto größer ist die Konzentration. Unten sind die beiden extremen Situationen dargestellt, die gleichmäßge Aufteilung der Objekte auf die gesamte Menge und die vollständige Konzentration, bei der ein Element alle Objekte auf sich vereint und alle anderen Elemente leer ausgehen.
 |
 |
Werden mehrere gleichartige Gesamtheiten gegenüberstellt, bieten die verschiedenen Lorenzkurven eine schnelle optische Vergleichsmöglichkeit. Siehe dazu auch das weiter unten folgende Beispiel mit den Agrarflächen in Bayern.
Ginikoeffizient
Als Ginikoeffizient G wird bezeichnet der Anteil der Fläche, die durch die Winkelhalbierende und die Lorenzkurve gebildet wird, an der Gesamtfläche unter der Winkelhalbierenden. Wenn vollkommene Konzentration besteht, ist die Fläche über der Lorenzkurve deckungsgleich mit dem Dreieck unter der Winkelhalbierenden. G ist dann 1. Bei fehlender Konzentration ist dann G=0.
Ermittlung des Ginikoeffizienten
Verbindet man die Punkte auf der Lorenzkurve mit den entsprechenden Punkten auf der Winkelhalbierenden, wird klar, dass wir es mit n vielen Trapezen zu tun haben, deren Flächen wir einzeln bestimmen und dann aufsummieren. Die Fläche eines Trapezes, wie in der Grafik angegeben, ermittelt man als
- .
Wir wollen die Fläche F3 des Trapezes zwischen den Abszissenwerten (x-Achse) 0,4 und 0,6 ermitteln. Man sieht, dass das Trapez im Vergleich zur obigen Grafik gekippt vorliegt. Die Höhe h ist also die Differenz
- .
Wir fassen a als linke Senkrechte von F3 als a auf: Dann ist
- .
Entsprechend beträgt die rechte Seite c
und wir erhalten als Fläche
- .
Allgemein: Die obige Fläche ergibt sich dann als

Es folgt beispielhaft die Berechnung des Gini in der Tabelle. Mit Tabellenkalkulation kann der Ginikoeffizient leicht ermittelt werden. Wir erhalten schließlich für den Ginikoeffizienten
|
i |
q*i |
S*i |
h*i |
ai |
ci |
0,5 · (ai+ci) |
0,5 · (ai+ci) · hi |
|---|---|---|---|---|---|---|---|
|
-- |
0 |
0 |
- |
- |
- |
- |
- |
|
1 |
0,025 |
0,2 |
0,2 |
0,175 |
0 |
0,0875 |
0,0175 |
|
2 |
0,1 |
0,4 |
0,2 |
0,3 |
0,175 |
0,2375 |
0,0475 |
|
3 |
0,225 |
0,6 |
0,2 |
0,375 |
0,3 |
0,3375 |
0,0675 |
|
4 |
0,475 |
0,8 |
0,2 |
0,325 |
0,375 |
0,35 |
0,07 |
|
5 |
1 |
1 |
0,2 |
0 |
0,325 |
0,1625 |
0,0325 |
|
Summe |
|
|
|
|
|
|
0,235 |
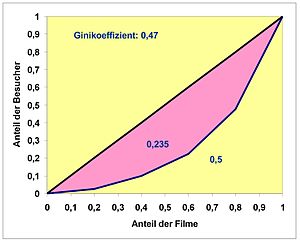
Metrisches Merkmal mit wenig möglichen Ausprägungen
Beispiel
Das interessierende Merkmal ist die Zahl der Autos in einem Haushalt. Es wurden 50 Haushalte befragt.

|
j |
xj |
nj |
Sj |
Sj* |
xjnj |
qj |
qj* |
|---|---|---|---|---|---|---|---|
|
1 |
0 |
10 |
10 |
0,2 |
0 |
0 |
0,00 |
|
2 |
1 |
20 |
30 |
0,6 |
20 |
20 |
0,27 |
|
3 |
2 |
10 |
40 |
0,8 |
20 |
40 |
0,53 |
|
4 |
3 |
5 |
45 |
0,9 |
15 |
55 |
0,73 |
|
5 |
4 |
5 |
50 |
1 |
20 |
75 |
1 |
|
Summe |
|
50 |
|
|
75 |
|
|
Lorenzkurve und der Ginikoeffizient berechnen sich im Prinzip wie oben, statt i wird hier der Index j verwendet. Der Merkmalsbetrag xi wird durch xj*nj ersetzt.
Klassiertes Merkmal
Hier wird die Klassenmitte x'j als Ersatz für den Merkmalswert xj verwendet.
Beispiel
|
Landwirtschaftliche |
Zahl der Betriebe | |
|---|---|---|
|
von ... bis ... unter |
1980 |
2003 |
|
2 - 10 |
112 |
43 |
|
10 - 20 |
78 |
34 |
|
20 - 30 |
34 |
18 |
|
30 oder mehr |
20 |
36 |
 |
 |
|
Klasse j |
Klassen- |
nj |
xj*nj |
Sj |
Sj* |
qj |
qj* |
|---|---|---|---|---|---|---|---|
|
2 - 10 |
6 |
112 |
672 |
112 |
0,4590 |
672 |
0,1683 |
|
10 - 20 |
15 |
78 |
1170 |
190 |
0,7787 |
1842 |
0,4614 |
|
20 - 30 |
25 |
34 |
850 |
224 |
0,9180 |
2692 |
0,6743 |
|
30 - 100 |
65 |
20 |
1300 |
244 |
1,0000 |
3992 |
1,0000 |
|
Summe |
|
244 |
3992 |
|
|
|
|
Wir erhalten als Ginikoeffizient für das Jahr 1980 den Wert 0,43 und für das Jahr 2003 den Wert 0,46.

![{\displaystyle x_{[1]}\leq x_{[2]}\leq ...\leq x_{[n]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db6c065df499cb5aebf211bccda41cc5d5748a39)

![{\displaystyle q_{i}=\sum _{k=1}^{i}x_{[k]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54e22225d21fbf7a259689f7d655e58899dc50a7)
















