Entropie: Physik
Zurück zur Übersicht

Man kann sich die Entropie als ein strömungsfähiges Etwas vorstellen, das in jedem Ding unserer Umwelt in größerer oder kleinerer Menge enthalten ist. Sie ist damit eine mengenartige Eigenschaft eines Körpers, d.h. sie bezieht sich auf einen Raumbereich und kann im weitesten Sinne wie ein „Stoff“ behandelt werden. So kann man sie in einem Materiebereich verteilen, anhäufen, einschließen oder umgekehrt daraus herauspumpen, ausquetschen, an einen anderen Gegenstand abschieben. Quelle: http://www.job-stiftung.de/pdf/skripte/Stoffdynamik/2.pdf
Anmerkungen zur Didaktik:[Bearbeiten]
Zitat: Die Entropie S ist eine Größe, für die Nichtphysiker eine sehr gute Anschauung haben und mit der sie intuitiv richtig operieren. Es gibt wahrscheinlich keine andere Größe, bei der der physikalische Begriff mit einem umgangssprachlichen Begriff so gut übereinstimmt: Die meisten umgangssprachlichen Aussagen, in denen das Wort Wärme oder Wärmemenge vorkommt, bleiben physikalisch korrekt, wenn man diese Wörter durch das Wort “Entropie” ersetzt. Quelle:F. HERRMANN SKRIPTEN ZUR EXPERIMENTALPHYSIK ABTEILUNG FÜR DIDAKTIK DER PHYSIK UNIVERSITÄT KARLSRUHE AUFLAGE 2003
Das Verständnis der Entropie in der Physik und Chemie wird außerordentlich durch die Arbeiten von Herrmann, Job und dem Karlsruher Physikkurs erleichtert. Folgenden Texte sind im Internet verfügbar und als Einstieg sehr empfehlenswert:
Sehr schön erklärt wird die Entropie in der Physik in folgendem Artikel: Handreichung Entropie Uni Koblenz
Vor allem sollte man die dort angeführten Übungsaufgaben durchrechnen, dann hat man schon viel begriffen.
Sehr empfehlenswert ist auch das Ebook Georg Job, Regina Rüffler: Physikalische Chemie. Teil 1: Grundzüge der Stoffdynamik. Siehe http://www.job-stiftung.de/index.php?id=8,22,0,0,1,0
Die Wärmelehre (Thermodynamik) wird sehr gut in folgendem Buch erklärt:
Einen weiteren Versuch die Entropie in der Physik anschaulich zu erklären, hat André Thess in seinem Buch Das Entropieprinzip - Thermodynamik für Unzufriedene, Oldenbourg-Verlag 2007, ISBN 978-3-486-58428-8 mit Hilfe des Prinzips der adiabatischen Erreichbarkeit unternommen.
Entropie bei einem Phasenübergang (Schmelzen, Verdampfen, etc.)[Bearbeiten]

In der Physik ist die Entropie einfach zu verstehen, wenn man den Übergang eines Stoffes in einen anderen Aggregatzustand betrachtet. Erstaunlicherweise wird dabei nur von latenter Wärme, aber selten von der Entropie gesprochen.
Man betrachtet z. B. einen Eisblock aus gefrorenem Wasser.
Will man diesen Eisblock auftauen, dann muss man am Gefrierpunkt Energie hineinstecken, ohne dass sich die Temperatur erhöht. Man spricht von der Schmelzwärme. Diese Energie dient nur dazu die bestehende Ordnung der festen Wasserteilchen aufzulösen, mehr Unordnung zu ermöglichen, das Wasser wird flüssig, die Unordnung wird größer, die Entropie wird größer.
Die Entropie beim Phasenübergang fest => flüssig entspricht der Schmelzwärme = der Schmelzenergie gemessen in Joule, da sich hier die Temperatur nicht ändert.
Diesen einfachen Umstand hat man sich auch für die Definition der Entropieeinheit zunutze gemacht:
Die Einheit der Entropie in der Physik ist 1 Joule / Kelvin.
1 Joule / Kelvin = Entropie, mit der man 0,893 cm3 Wassereis schmelzen kann. (Voraussetzung: Druck p = Normaldruck)
Man kann beim Phasenübergang die Energie also einfach durch die Temperatur des Phasenübergangs teilen und erhält die Entropiedifferenz des Vorgangs in Joule / Kelvin.
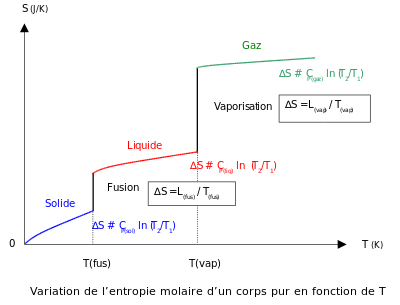
Ein sehr wichtiges Diagramm des Zusammenhanges der Entropie und der Temperatur Leider nur in Französisch.
Entropie beim Mischen eines Stoffes von zwei Teilen mit verschiedener Temperatur[Bearbeiten]
Es wird eine Mischung von Wasser aus einem warmen und einem kalten Anteil betrachtet.
-------------- | | | T(w) | | warm | | | | | | ------| dE --- | V | | | | kalt | | T(k) | | | --------------
Für den kälteren bzw. wärmeren Anteil ist die Änderung der Entropien dS (Delta oder Differenz S) wie folgt definiert:
Wobei E die Wärmeenergie ist, die von dem warmen zum kalten Flüssigkeitsanteil fließt TK ist die Temperatur in Kelvin des kalten Anteils TW ist die Temperatur in Kelvin des warmen Anteils
Die gesamte Entropieänderung erhält man durch folgende Gleichung:
Dabei ist dS > 0, da TW > TK. Beachte: Die Temperaturen stehen im Nenner.
Bei diesem freiwillig ablaufenden Vorgang ist die Entropieänderung dS > 0. Erreicht die Temperatur des warmen Körpers die des kalten Körpers ist ein Gleichgewicht erreicht und der Wärmeaustausch kommt zum Erliegen.
Beispiel 1: Mischung desselben Stoffes derselben Menge unterschiedlicher Temperatur[Bearbeiten]
Man füllt ein Styroporgefäß mit 300 g Wasser, das eine Temperatur von 40 Grad Celsius aufweist. Dann schüttet man 300 g Wasser von 10 Grad Celsius dazu. Das Styroporgefäß als guter Isolator nimmt nur eine minimaler Wärmemenge auf. Dann rührt man etwas herum und misst die Mischtemperatur 24,8 Grad Celsius. Als Schätzung müsste eine Mischtemperatur von 25 Grad herauskommen.
Wie kann man die Mischtemperatur errechnen?
Es gelten folgende Regeln:
- Die Energieabgabe EW der wärmeren Flüssigkeit ist gleich der Energieaufnahme EK der kälteren Flüssigkeit.
EW = EK
- Die Masse der wärmeren Flüssigkeit ist gleich der Masse der kälteren Flüssigkeit.
mW = mK
- Die spezifische Wärmekapazität des Wassers ist:
Die Temperaturen werden wie folgt bezeichnet:
- tW = 40 °C
- tK = 10 °C
- tmisch = gesucht
Es gilt folgende Formel:
EW = cWasser * m W * (tW − tmisch)
EK = cWasser * m K * (tmisch − tK)
Da EW = EK gilt, kann man vereinfachen:
cWasser * m W * (tW − tmisch) = cWasser * m K * (tmisch − tK)
Aus dieser Gleichung kürzt man cWasser. Man dividiert auf beiden Seiten durch cWasser.
m W * (tW − tmisch) = m K * (tmisch − tK)
Da im obigen Beispiel mW = mK gilt, kann man auch noch m kürzen. Es bleibt folgende Formel übrig:
(tW − tmisch) = (tmisch − tK)
Jetzt setzt man die Temperaturen ein und errechnet die Mischtemperatur:
(40 °C − tmisch) = (tmisch − 10 °C)
Jetzt rechnet man die Gleichung nach tmisch aus. Man addiert auf beiden Seiten tmisch.
40 °C − tmisch + tmisch = tmisch − 10 °C + tmisch
40 °C = 2 * tmisch − 10 °C
Man addiert auf beiden Seiten 10 °C.
50 °C = 2 * tmisch
Man dividiert beiden Seiten durch 2.
50 °C / 2 = tmisch tmisch = 25 °C
Was hat dies alles nun mit der Entropie zu tun?
Man kann aus dem obigen Beispiel jetzt auch die Entropie berechnen:
Es gilt dS = dE / TK − dE / TW
Die Temperatur muss man allerdings in Kelvin einsetzen:
TW = (40 Grad + 273 Grad) Kelvin TK = (10 Grad + 273 Grad) Kelvin
Die Energieaufnahme und -abgabe sind gleich:
EW = cWasser * m W * (tW − tmisch)
E = 4,19 J/ (g * Grad Celsius) * 300 g * (40 Grad Celsius − 25 Grad Celsius) E = 4,19 J/ (g * Grad Celsius) * 300 g * 15 Grad Celsius E = 1257 J /Grad Celsius * 15 Grad Celsius E = 18855 Joule
Daraus kann man die Entropieänderung errechnen:
dS = 18855 Joule / 283 Kelvin − 18855 Joule / 313 Kelvin dS = 66,625 − 60,24 Joule / Kelvin dS = 6,385 Joule / Kelvin
Interessant bei der ganzen Rechnung ist die Tatsache, das
- die Energie, die vom wärmeren Wasser an das kältere Wasser abgegeben wurde identisch ist mit der Energie, die das kalte Wasser aufgenommen hat.
- die Entropie des gemischten Wassers aber grösser geworden ist als die Summe der Einzelentropien vor der Mischung.
Basisgrößen der Thermodynamik und einfache Sätze[Bearbeiten]
Es gibt in der Wärmelehre drei Basisgrößen:
- die Energie E
- die Temperatur T
- die Entropie S
Die Größen finden folgende Analogie in der Elektrizitätslehre:
| Thermodynamik | Elektrizitätslehre |
|---|---|
| Temperatur | elektrisches Potential |
| Temperaturdifferenz | Spannung |
| Entropie | elektrische Ladung |
| Energie | Energie |
Im Gegensatz zur elektrischen Ladung ( positiv und negative Werte) kann die Entropie nur positive Werte annehmen.
Mit diesen 3 Größen kann man einfach verstehbare Sätze über die Entropie formulieren: (Quelle Handreichung Energie und Entropie)
- Jeder Körper enthält Entropie, wenn seine Temperatur über dem absoluten Nullpunkt liegt.
- Die Entropie kann nur positive Werte annehmen.
- Je größer die Masse eines Gegenstandes ist, desto mehr Entropie enthält er, vorausgesetzt die Temperatur bleibt gleich.
- Je heißer ein Körper ist, desto mehr Entropie enthält er. Die Entropie ist also temperaturabhängig.
- Die Entropie fließt von ganz allein von einer Stelle höherer Temperatur zu einer Stelle niedriger Temperatur, wenn ein Austausch zwischen den Stellen möglich ist.
- Eine Temperaturdifferenz Delta T ist also der Anlass für einen Entropiefluss
- Je größer die Temperaturdifferenz desto größer ist der Entropiefluss unter der Voraussetzung unveränderter Materialien.
- Der Entropiefluß I ist die Entropie, welche pro Zeiteinheit geflossen ist.
VORSICHT: Nicht Groß T ( Temperatur) mit klein t (Zeit) verwechseln.
Analogie Thermodynamik und Elektrizitätslehre für abgeleitete Größen[Bearbeiten]
Thermodynamik Elektrizitätslehre --------------------------------------------------------------------------------- Entropiewiderstand elektrischer Widerstand IS = Entropiefluß ΔS/Δt (t = Zeit) Ladungsfluß Ladung Q /Zeit = Stromstärke IQ Entropiekapazität CS=ΔS/ΔT elektrische Kapazität C= Ladung Q/ Spannung U IE = Energiefluß = ΔE/t = Leistung IE = Energiefluß = ΔE/t = Energie/Zeit = Leistung IE = T * IS IE = elektr.Pot * IQ ΔE = T * ΔS ΔE = elektr.Pot * ΔQ
- Jedes Material setzt dem hindurchfließenden Entropiestrom einen Widerstand entgegen.
- Dieser Widerstand ist um so größer, je kleiner die Austauschfläche A der Leitung und je größer die Länge l der Leitung ist.
- Dieser Widerstand hängt außerdem vom wärmeleitenden Material ab. Diese Materialkonstante nennt man rhoS.
- Für den Entropiewiderstand gilt also:
RS = l / A * rhoS
- Der Entropieleitwert ist der Kehrwert des Widerstandes. Er berechnet sich als
(T = Temperatur).
Dies nennt man das Fouriersche Gesetz.
- Die Entropiezunahme eines Körpers bei Erhöhung der Temperatur nennt man Entropiekapazität CS. Sie berechnet sich als
- Die Entropiekapazität hängt vor allem von der Temperatur, aber auch von der Masse, dem Volumen, dem Druck und der Stoffmenge ab.
- Bei Phasenübergängen wie dem Schmelzen und Verdampfen ändert sich die Entropiekapazität sehr stark.
- Entropie kann neu erzeugt werden durch
- Reibung
- eine chemische Reaktion
- durch elektrische Ströme in elektrischen Widerständen
- durch Entropieströme in Wärmewiderständen.
- Entropie kann zwar erzeugt, aber in der Summe nicht verringert werden.
- Vorgänge, bei denen Entropie erzeugt wird, können von alleine nicht wieder rückwärts ablaufen. Sie sind irreversibel.
- Die Entropie ist ein Energieträger. Liegt ein Entropiefluss vor, so ist dieser immer von einem Energiefluss begleitet.
- Die den Entropiefluss IS begleitende Energiefluß (Energiestromstärke) IE berechnet sich zu
Lässt man den Faktor Zeit aus der Formel auf beiden Seiten wegfallen, dann ergibt das:
- Die Energiestromstärke entspricht einer Leistung (Energie / Zeit).
P = IE
- Versucht man mit verschiedenen Arten des Wärmeentzugs einem Körper immer mehr Energie zu entziehen, kann man zwei Tatsachen feststellen:
- Man kommt zwar der Temperatur Null Kelvin (-273.15 Grad Celsius) sehr nahe, kann sie aber nicht unterschreiten bzw. erreichen. Bei dieser Temperatur befindet sich ein absoluter Temperaturnullpunkt.
- Bei dieser Temperatur kann man keine Entropie mehr entziehen. Absolut kalte Körper haben keine Entropie mehr.
- Die Einheit der Entropie in der Physik ist 1 Joule / Kelvin.
- 1 Joule / Kelvin entspricht der Entropiemenge, mit der man bei Normaldruck 0,893 cm3 Wassereis schmelzen kann.
- Manche Autoren verwenden das Carnot (Einheitenzeichen: Ct) aus didaktischen Gründen als besonderen Namen für die SI-Einheit Joule durch Kelvin (J/K) der Entropie.
Messung der Entropie[Bearbeiten]
Entgegen einer weit verbreiteten Meinung ist die Entropie in der Physik relativ einfach zu messen.
Ein einfaches Beispiel zeigt die Messung der Schmelzwärme oder der Verdampfungswärme verschiedener Stoffe. Da hier die Temperatur konstant ist, kann man die ermittelte Energie direkt der Entropie gleichsetzen.
Peltierelement[Bearbeiten]
Entropieströme durch eine Fläche lassen sich mit einem geeichten Peltier-Element messen.
Siehe www.heise.de/tp/r4/artikel/5/5856/1.html
Rechenaufgaben[Bearbeiten]

Aufgabe 0[Bearbeiten]
Sie haben 1 Liter Wasser von 20 Grad. Dazu gießen Sie einen weiteren Liter Wasser von 20 Grad dazu. Frage a: Wie hoch ist danach die Temperatur des Wassers ? Frage b: Wie groß ist danach die Entropie`?
Antwort: Die Temperatur bleibt gleich. Die Entropie verdoppelt sich.
Aufgabe 1[Bearbeiten]
1. Sie haben 1 kg Eis bei Null Grad Celsius und normalem Umgebungsdruck. Berechnen Sie die Zunahme der Entropie, wenn das Eis komplett zu Wasser von 0 Grad geschmolzen ist. Benutzen Sie dazu die spezifische Schmelzwärme von Wasser.
- Lösung: S = 1219,848 Joule / Kelvin
- Lösungsweg: Siehe Entropie: Loesungen
1a. Sie haben 5 kg Wasser beim normalen Siedepunkt von 100 Grad Celsius und normalem Umgebungsdruck. Berechnen Sie die Zunahme der Entropie, wenn das Wasser komplett zu Wasserdampf mit der Temperatur des Siedepunktes verdampft ist. Benutzen Sie dazu die spezifische Verdampfungswärme (Verdampfungsenthalpie) von Wasser. (Siehe de.wikipedia.org/wiki/Verdampfungswärme#Verdampfungsenthalpie)
- Lösung: S =
- Lösungsweg: Siehe Entropie: Loesungen
1b. Warum muss bei dem Vorgang Energie aufgewendet werden und warum läuft die Verdampfung nicht von alleine ab? Wann läuft die Verdampfung scheinbar von alleine ab?
1c. Kommt es bei dem Übergang Wasser > Wasserdampf zu einer Entropiezunahme oder Entropieabnahme?
1d. Wie kann man sich erklären, das Wasser auch bei normalen Luftdruck auch schon bei Temperaturen weit unter dem Siedepunkt verdampft z. B. bei der Trocknung eines Wäschestückes auf der Wäscheleine?
Aufgabe 2[Bearbeiten]
2. Sie erwärmen 1 kg Wasser von 20 Grad Celsius auf 70 Grad Celsius. Wieviel Energie müssen Sie dazu verwenden? Wie groß ist die Entropiezunahme?
- Lösung: S =
- Lösungsweg: Siehe Entropie: Loesungen
Aufgabe 3[Bearbeiten]
3. Sie mischen 1 kg Wasser von 20 Grad Celsius und 1 kg Wasser von 50 Grad Celsius. Wieviel Energie geht vom wärmeren Wasser auf das kältere Wasser über? Wie hoch ist die Mischtemperatur? Wie groß ist der Entropieanstieg?
- Lösung: S =
- Lösungsweg: Siehe Entropie: Loesungen
Aufgabe 4[Bearbeiten]
10 kg Stickstoff werden isobar auf 1/10 des Anfangsvolumens verdichtet .
- Wie ändert sich der Druck ?
- Wie ändert sich die Temperatur ?
- Wie ändert sich die Entropie ?
- Wieviel mechanische Energie muß dafür aufgewendet werden ?
Aufgabe 5[Bearbeiten]
Die spezifische Wärmekapazität des Wassers Cw ist bei p = 1 atm gleich 4,19 J / (g*K). Erklären Sie diesen Wert für 1 g Wasser und 1 Grad Kelvin Temperaturerhöhung.
Aufgabe 6[Bearbeiten]
Welche Wassermenge hat bei 50 Grad die gleiche Wärmemenge (Entropie ) wie 2000 g Wasser bei 20 Grad Celsius ?
Aufgabe 7[Bearbeiten]
Der Heizdraht eines 1200-W-Haarföns hat eine Temperatur von 1000 K.
- Wie viel Entropie wird pro Sekunde im Heizdraht erzeugt?
Aufgabe 8[Bearbeiten]
Berechnen sie die Entropie die notwendig ist, um 5 kg Eis bei Null Grad Celsius und p = 1 atm zum Schmelzen zu bringen.
Wie kann man das berechnete Ergebnis mit einem Tauchsieder meßtechnisch überprüfen ?
Wie unterscheidet sich der Wert der Entropie, die dafür notwendig ist, vom errechneten Wert der Energie ?
Aufgabe 9[Bearbeiten]
Berechnen sie die Entropie die notwendig ist, um 5 kg Wasser von Null Grad Celsius und p = 1 atm auf 10 Grad Celsius und gleichbleibendem Druck zu erwärmen ?
Wie kann man das berechnete Ergebnis mit einem Tauchsieder meßtechnisch überprüfen ?
Aufgabe 10[Bearbeiten]
Wie ändert sich die Entropie S in einem Stück Metall mit der Masse m = 0,001 kg beim Anstieg der Temperatur von 1 Grad Kelvin auf 11 Grad Kelvin ?
Nehmen Sie dazu an, daß die spezifische Wärmekapazität c des Metalls konstant 500 J/kg/Kelvin beträgt.
Benutzen Sie folgende Formel:
T2 ist die Temperatur 11 Kelvin T1 ist die Temperatur 1 Kelvin ln = Logarithmus zur Basis e (natürlicher Logarithmus)
Lösung:
Delta S = 500 J/kg/Kelvin * 0,001 kg * ln ( 11 / 1 ) Delta S = 0,5 J/K * 2,397 Delta S = 1,2 J/K
Aufgabe 11 Mischung von Gasen[Bearbeiten]
Ein 10-Liter Behälter ist in zwei gleiche Hälften geteilt. In einer befindet sich Stickstoff mit einem Druck von 1 bar, in der anderen Hälfte Wasserstoff von 1 bar. Die Temperatur ist 20 Grad Celsius.
- Wie ändert sich die Entropie S und die freie Enthalpie G des Gesamtsystems, wenn man eine Vermischung zulässt ?
- Wie lange dauert es , bis eine gleichmässige Vermischung der beiden Gase erreicht ist ?
- Wie groß ist ΔS und ΔG, wenn der Wasserstoff durch Stickstoff ersetzt wird ?
Aufgabe 12 Mischung von 2 idealen Gasen[Bearbeiten]
Wir mischen zwei Gase adiabatisch mit gleichen Volumina, gleicher Temperatur, gleicher Teilchenzahl . Beispielsweise 1 Mol Helium und 1 Mol Neon.
Berechnen Sie mit der Boltzmann Konstante k und der Avogadroschen Zahl die Mischungsentropie.
Daraus ergibt sich:
- DeltaS = k * NA * ln (( NA + NA ) / NA ) + k * NA * ln (( NA + NA ) / NA)
- DeltaS = 2*k *NA * ln 2
- DeltaS = 2* 1,380*10^-23 J/K* 6,02214179*10^23 1/mol*ln2
- DeltaS = 2*1,4*6,02*0,69 J/K/mol
- DeltaS = 11,68 J/K/mol
Aufgabe 13[Bearbeiten]
Sie betrachten ein Gas mit folgenden Vorgaben:
- Temperatur 290 K
- Volumen 1 m3
- Druck 1,5 bar
Berechnen Sie die Gesamtentropie des Gases.
- Welche Formel wollen Sie benutzen ?
- Wie lautet das Ergebnis ?
- Welche Einheit hat das Ergebnis ?
- Wie kann man das Ergebnis interpretieren ?
Zweiter Hauptsatz der Thermodynamik[Bearbeiten]
Jeder Körper enthält Entropie.
Entropie kann nur zusammen mit Wärme von einem Körper zu einem anderen Körper übertragen werden.
Dabei gilt: Übertragene Wärme / übertragene Entropie = Temperatur
Entropie kann produziert aber niemals vernichtet werden.
In einem abgeschlossenen System kann die Gesamtentropie nicht abnehmen. Sie bleibt im Laufe der zeitlichen Entwicklung dieses Systems entweder konstant oder sie nimmt zu.
Für abgeschlossene Systeme gilt:
Verweise[Bearbeiten]
- www.wiwi.uni-frankfurt.de/~rainerh/Diplomarbeit/dbdzh03.htm
- 2. Hauptsatz gut lesbar erklärt
- de.wikipedia.org/wiki/Thermodynamik
- Thermodynamik
Nullpunktentropie[Bearbeiten]
Aus theoretischen Erwägungen heraus müssten Kristalle am absoluten Nullpunkt eigentlich die Entropie 0 haben. Das ist jedoch selten der Fall. Meist schaffen es reale Kristalle, nach dem sie einmal erstarrt sind, nicht mehr, die ideal mögliche Kristallordnung mit 0 Entropie anzunehmen. Die messbare reale, von 0 verschiedene Entropie der Kristalle am absoluten Nullpunkt der Temperatur wird Nullpunktentropie genannt.
Thermodynamisches Gleichgewicht[Bearbeiten]
Jedes abgeschlossene thermodynamische System, in dem gewisse Austauschprozesse frei möglich sind, nimmt nach dem Abklingen der Prozesse einen Gleichgewichtszustand an. Dieser ist bestimmt durch das Maximum der Entropie dieses Systems.
siehe auch Definition der Entropie über das Prinzip der adiabatischen Erreichbarkeit.
Lokale Entropieabnahme[Bearbeiten]
Es gibt viele Beispiele für eine lokale Entropieabnahme, die vermeintlich dem 2. Hauptsatz widersprechen, die aber durch eine Gesamtbetrachtung schlüssig erklärt werden können. Es entstehen geordnete Strukturen aus vorher ungeordneten. Gleichzeitig wird aber dafür die Entropie insgesamt trotzdem größer
Beispiele[Bearbeiten]
- Sternentstehung durch Gravitation
- Kristallisation von Stoffen beim Abkühlen
- Lebensentstehung auf der Erde
- Evolution des Lebens auf der Erde.
Auch die Vorstellung vom Urknall geht von einem sehr entropiearmen Anfangszustand aus. Irgendwie muss dieser entropiearme Zustand erreicht worden sein.
Entropieformel von Boltzmann[Bearbeiten]
Zitat aus dem Spiegel Wissenslexikon http://www.spiegel.de/lexikon/54415448.html
L. Boltzmann erkannte, dass der Entropiesatz gleichbedeutend ist mit folgender Wahrscheinlichkeitsaussage: Die auf die einzelnen Moleküle eines Körpers verteilte Bewegungsenergie geht stets von einem weniger wahrscheinlichen Verteilungszustand in einen wahrscheinlicheren über, nicht aber umgekehrt. Sind z. B. alle Luftmoleküle zu Anfang in einer Ecke eines Zimmers, so verteilen sie sich gleichmäßig in diesem Zimmer: die Entropie nimmt zu. Es ist jedoch praktisch ausgeschlossen, dass umgekehrt die gleichmäßig verteilten Moleküle sich einmal alle in einer Zimmerecke ansammeln.
Vom Ersten zum Zweiten Hauptsatz[Bearbeiten]
Den Entropiebegriff haben Physiker erfunden. Um den naturkundlichen Hintergrund zu beleuchten, ist es wohl nicht verkehrt, etwas auszuholen. Wie kam die Forschung zuerst auf diese Maßzahl "Entropie", und wie entwickelte sich dann ihre Bedeutung? Die Entropie entstand, als die Wärmelehre und die Mechanik sich trafen.
Die Eigenschaften eines relativ homogen erscheinenden Stücks von Materie sollten mit relativ wenigen zahlenwertigen Variablen erfasst werden. Zum Beispiel das Zeug im Gasraum einer Kolbenmaschine wie Dampfmaschine oder Verbrennungsmotor. Oder ein Gemisch von Substanzen in einem Reaktionsgefäß. Man unterschied intensive und extensive Zustandsvariablen. Die erste Art hängt nicht von der geometrischen Größe des Objekts ab: Temperatur, Druck, Konzentrationen. Die zweite Art ist streng proportional zur Größe, wie Volumen, gespeicherte Energie, Masse. Die intensiven Variablen gibt es eindeutig, wenn eine homogene Substanz angenommen werden kann.
Es schälte sich eine Gesetzmäßigkeit heraus, ganz besonders die Formel des idealen Gases. Eine Relation mit den vier Variablen (Druck,Volumen,Masse,Temperatur). Der starke Eindruck entstand, dass die makroskopischen Zustände aus mikroskopischen Eigenschaften folgen. Wird statt der Masse die Anzahl der Moleküle N eingesetzt, dann gehorchen alle Gase ungefähr derselben Relation
- p V = N k T.
Mit der absoluten Temperatur T (in Kelvin gemessen) und der universellen Boltzmann-Konstanten k.
Seit der Erfindung der Dampfmaschine war es wichtig zu wissen, wie genau eine "Wärme" in mechanische "Arbeit" umgesetzt wird. Was sind die Bilanzen zwischen Wärme-Energie und makroskopischer mechanischer Energie? Haben wir eine Zustandsfunktion der im Gas gespeicherten Energie, etwa U = U(p,T,N) als eine extensive Größe? Die Energie kann sich ändern mit Hilfe der Mechanik oder auch nicht. Wenn das Gas unter Druck einen Kolben verschiebt, leistet es hochwertige Arbeit. Wird das Gas bei unverändertem Volumen in ein Wasserbad getaucht und verliert seinen Druck durch Abkühlen, dann entschwindet ihm Energie nur als schnöde Abwärme.
Carnot analysierte scharfsinnig, wie sich ein Gas auf verschiedenen Wegen durch seinen "Zustandsraum" bewegt, also im einfachsten Fall in der zweidimensionalen Ebene mit den Koordinaten (p,V) oder etwa (p,T). Je nach dem Pfad ändert sich die innere Energie zum Teil durch die Abgabe und Aufnahme von mechanischer Arbeit A, zum Teil durch die Diffusion oder Strahlung von Wärme Q. Natürlich wollte man die beste Strategie finden, die den meisten Nutzen aus einer Wärmekraftmaschine herauskitzelt. Den optimalen Wirkungsgrad also. Man stellt sich eine "infinitesimale" Variation (dp,dT) vor und man sucht die Bilanz für diesen kleinen Schritt:
- Erster Hauptsatz: dU = δA + δQ.
Die Existenz der Zustandsfunktion U ist gleichbedeutend mit dem Satz von der Energieerhaltung, dem Ersten Hauptsatz. Die innere Energie ändert sich nur durch Austausch mit der Umgebung von mechanischer Arbeit und/oder von Wärmeenergie. Werden alle Teile eines abgeschlossenen Systems zusammen verrechnet, ist die gesamte Energie konstant.
Doch was sollen diese zwei verschiedenen Buchstaben "d" und "delta" bei der Gleichung? Der Unterschied wiegt schwer.
Die Mathematik erfand den Begriff Differenzialform für Objekte, die auf einem n-dimensionalen Raum definiert sind und aussagen, wie an jedem Punkt und für jeden Richtungsvektor dort ein relevanter Wert abdriftet. Auch Pfaffsche Formen, 1-Formen oder Formen erster Ordnung genannt. Man unterscheidet die gutartigen exakten Formen und die schlechten weniger exakten. Eine exakte Form entsteht durch Ableitungen aus einer Zustandsfunktion. Ein d-Operator wie hier:
- U(p,T) →→ dU(p,t; dp,dt) = (∂U/∂p) dp + (∂U/∂T) dT.
(p,T) ist unser Punkt und (dp,dT) ist der Richtungsvektor, angeheftet an dem Punkt. dU ist daher eine Linearform auf der Menge der Richtungsvektoren oder Tangentialvektoren. Eine nicht-exakte Form — dass soll ein "delta" andeuten — muss dagegen durch zwei (oder allgemein n) beliebige Funktionen angegeben werden, die sich nicht aus einer Stammfunktion durchs Differenzieren herleiten. Zum Beispiel
- δQ = δQ (p,T; dp,dT) = Q¹(p,T) dp + Q²(p,T) dT.
Man sagt auch, exakte Formen sind integrierbar und die anderen eben nicht. Noch anderer Jargon, exakte Formen sind totale Ableitungen. Wegen der Vertauschbarkeit von partiellen Ableitungen ist die notwendige Bedingung für Exaktheit, dass die gekreuzten Ableitungen verschwinden,
- (∂Q²/∂p) - (∂Q¹/∂T) =?= 0.
In einem n-dimensionalen Zustandsraum verkörpert die Liste solcher Paare ( n(n-1)/2 Stück ) die äußere Ableitung einer 1-Form. Die ist eine 2-Form, ein antisymmetrischer Tensor.
Die 1-Formen sind die natürlichen Integranden über Wege oder Kurven, also über eindimensionale Gebilde im Zustandsraum. Das heißt, Koordinatenwahl und Parametrierung der Kurve fallen raus im Ergebnis. Nur für die exakten Formen verschwindet das Integral über geschlossene Wege und ein Integralwert zwischen zwei Endpunkten ist unabhängig vom Weg die Differenz der Stammfunktions-Werte.
Zurück zum Thema. Ein physikalisches Objekt hat in jedem Zustand eine gespeichterte Energie U, aber unbekannte Summen der eingeflossenen Arbeit A oder Wärme Q. Unser Modell kennt keine separaten Stammfunktionen für die Wärme und für die mechanische Arbeit, die eine Gasmenge empfängt oder liefert. Deren aufsummierten Bilanzen sind stark abhängig vom eingeschlagenen Weg durch die Zustands-Mannigfaltigkeit.
Der Durchbuch bei Carnot in der Wärmelehre war die Aussage, dass es zusätzlich zur exakten Form der Energie-Entwicklung (dU) eine andere exakte Form gibt, nämlich die Ableitung der Entropie S. Mit S ist das unexakte Objekt δQ bei reversiblen Vorgängen bis auf einen Faktor T nun doch eine totale Ableitung!
- δQ = T · dS mit einer Funktion S(p,T,...).
Den idealisierten reversiblen Austausch von Wärme stellt man sich so vor, dass eine "unendliche" Menge von Wärmebädern benutzt wird. Immer ist genau das mit der jeweiligen Temperatur im Kontakt mit dem Testgas in einem Kolben. Genauso sind beim reversiblen Austausch von Arbeit der Außendruck und der Innendruck idealerweise gleich.
- Satz von Carnot: dU = δA + T dS ; (reversible Prozesse).
Wir haben nun ein Paar von extensiven Zustandsfunktionen (U,S), die innere Energie und die Entropie. Daraus kombiniert man gern die Freie Energie F := U - TS. Zustandsfunktion F gibt an, wieviel mechanische Arbeit aus dem System bei einem isothermen reversiblen Prozess abgesaugt werden kann.
Beweis. Der d-Operator benimmt sich nach der Produktregel,
- dF = dU - d(TS)= (δA + T dS) - (T dS + S dT).
Also: δA = dF + S dT. Auf einer Kurve mit T=const ist das Integral des Terms (S dT) gleich Null und es bleibt das Integral über das exakte dF, gleich der Differenz der F-Werte an den Enden.
Folgerung. Ein isothermer Kreisprozess kann daher überhaupt keine Arbeit liefern. Eine wirkliche Maschine braucht irgendwie Speicher bei verschiedenen Temperaturen.
Ein weiterer Durchbruch war der Zweite Hauptsatz, der die gesamte Entropie eines abgeschlossenen Systems betrifft. Ein solches System sei anfangs inhomogen und seine Entropie S sei die Summe aus den Entropien der Teile. Dann kann die Entropie als Funktion der Zeit nur anwachsen. Die makroskopischen Zustandsgrößen beschreiben daher eine Zeitentwicklung, die nur in Ausnahmefällen umkehrbar ist. Im Allgemeinen geht Ordnung spontan in Chaos über.
- Zweiter Hauptsatz: (dS/dt) ≥ 0. (abgeschlossene Systeme)
In einem offenen System dagegen, das wie unseres ständig von der Sonne wertvolle Energie empfängt, kann stellenweise Entropie sinken, aufgeräumt werden, neue Ordnung entstehen, Leben sich vermehren. Irgendwo nebenan wird dann mit hochgradig entropischem Abfall bezahlt.
Jedes hinreichend isolierte System entwickelt sich irreversibel. Die Zeit hat eine Richtung. Niemand kann sich in der Zeit vorwärts und rückwärts bewegen, wie es im Raum der Fall ist. Stellt sich die Frage: Wie kommt es, dass die Theorie auf der atomaren Ebene zeitsymmetrische Gleichungen hat, aber das Kollektiv hat keine mehr?
Die mikroskopische Theorie[Bearbeiten]
Ein dritter Durchbruch war die Statistische Mechanik. Mit der Kinetischen Gastheorie gelang es allen voran Maxwell und Boltzmann, die makroskopischen Formeln aus der mikroskopischen Bewegung von Molekülen herzuleiten. Boltzmann schaffte es auch, die Entropie als eine statistische Eigenschaft dieser Haufen von Teilchen zu formulieren. Hier ziehen die Begriffe "Wahrscheinlichkeit" und "Informationsmenge" in die Physik ein. Versuchen wir, schlecht und recht zu definieren, was gemeint sein kann.
Die Wärme ist die Bewegung einer großen Menge von Atomen oder Molekülen, die wie die Billiardkugeln der klassischen Mechanik gehorchen. Heutzutage wirkt der Ausgangspunkt der Betrachtungen selbstverständlich. Damals bekam Boltzmann noch Gegenwind von lautstarken, erzkonservativen Gelehrten wie Ernst Mach, die Zweifel nährten an der Atomistik.
Die gespeicherte Energie U in einem Gas ist die Summe der kinetischen Energien der Atome oder Moleküle. Die absolute Temperatur T ist proportional zur mittleren kinetischen Energie eines Freiheitsgrades der Flugbewegung. Es gibt 3 Freiheiten der Translation, wir leben in drei Dimensionen. Bei dem Fluss von Wärmeenergie Q übertragen elastische Zusammenstöße und/oder infrarote Lichtquanten ungeordnet die kinetische Energie: mehrheitlich von den schnelleren auf die langsamen Moleküle. Beim Austausch einer Arbeit A wandelt sich die ungerichtete Bewegung der Moleküle in makroskopische sichtbare um; alle Teilchen werden in eine Richtung gezwungen.
Makroskopisch sei unser System beschrieben als ein Punkt in einem Zustandsraum, etwa ein Tripel (p,V,T). Andererseits ist das System mikroskopisch eine Menge von N Atomen i=1...N, von denen jedes einen Ort hat und einen Impuls .
Man fragt sich, wie viele verschiedene Werte in diesem extrem hochdimensionalen mikroskopischen Phasenraum zum vorgegebenen makroskopischen Zustandspunkt gehören, genauer gesagt zu einen kleinen 'Volumenelement' um diesen Punkt herum. Es sind unglaublich viele. Die statistische Verteilungsfunktion w von Maxwell-Boltzmann gibt an, wie bei gegebener Temperatur T die Ziehung der Lose ausgeht, als könnte man die Mikrozustände aus einer Lotterie bekommen.
Es bezeichne E(x,p) die gesamte Energie des Atomhaufens als Funktion der Orte und Impulse. Dann ist eine brauchbare Verteilungsfunktion w = exp(-E/kT), bis auf einen Normierungsfaktor. Der Jargon nennt sie die Kanonische Gesamtheit. Sie ist als Integrand über sämtliche atomaren x- und p-Variablen zu verstehen. Sie gilt als Modell für das System im Wärmebad bei konstanter Temperatur, nicht unbedingt bei konstanter Gesamtenergie. Sitzt das System in einem bekannten Volumen, müssen alle Atomkoordinaten darauf beschränkt sein.
Integriert man eine kanonische Gesamtheit über die 'Schalen' konstanter Gasamtenergie E, kommt eine eindimensionale Energieverteilung v(E) dE heraus. Die ist äußerst scharf um einen Erwartungswert konzentriert, obwohl die einzelnen Atome ziemlich breit gestreute Energien haben dürfen. Es ist also doch erlaubt, so ungefähr "konstante Energie" und "konstante Temperatur" zu verwechseln. Boltzmann fand heraus, dass die Entropie nach der Formel zu berechnen ist. k ist seine berühmte Konstante, ln der natürliche Logarithmus und ist das Volumen der Phasenschale am Erwartungswert der Energie. Genauer das Teilvolumen, das den zu analysierenden makroskopischen Zustand darstellt. Zählt man den Phasenraum in Einheiten des Wirkungsquantums, ist die Entropie (bis auf den Faktor k) der Logarithmus der Zahl der möglichen Quantenzustände. Die Zahl aller vollständig bis ins kleinste Detail vermessenen Zustände, die jedoch bei einer groben Charakerisierung gleich aussehen. Wir sagen, die Entropie ist der Logarithmus der Unkenntnis, denn niemand weiß, welcher der Mikrozustände vorliegt. Nur ein 'Dämon' wäre in der Lage, einen Mikrozustand von astronomisch vielen Atomen zu messen.
Die Wahrscheinlichkeitsdichte w ist eine positiv definite Funktion der Orte und Impules aller Teilchen. Eine Funktion auf dem Phasenraum, deren totales Integral Eins ergibt. Das 'Gewicht' eines Makrozustands wie (p,V,T,...) ist das Integral dieser Mikroverteilung w über das Teilgebiet des Phasenraums, das auf den gegebenen Makrozustand abgebildet wird. Je nachdem wie die makroskopische Lage aussieht, ist ihr Ursprungsgebiet im Phasenraum mehr oder weniger groß. Das Gewicht ist dieses Boltzmannsche Phasenvolumen. Wird es nicht mit W bezeichnet auf seinem Grabstein (S = k ln W) und manchmal als 'Wahrscheinlichkeit' ausgesprochen? Das ist aber missverständlich ohne die richtige Ausdeutung.
Man vergleicht nun inhomogene Makrozustände mit solchen, die homogen sind. Beispielsweise seien zwei Tripel (p',V',T') und (p",V",T") nötig, weil das Gas im Teilvolumen V' einen anderen Druck und/oder eine andere Temperatur hat als im Teilgebiet V". Man durchmischt nun das Ganze, indem man eine imaginäre Wand zwischen den Teilen entfernt und einen homogenen Zustand (p,V,T) erreicht.
Der Einfachheit halber, weil bei gegebenen Temperaturen die Gesamtenergie scharf definiert ist, gehen wir zur Mikrokanonischen Gesamtheit über. Das heißt, zu einer 'Schale', einer Mannigfaltigkeit im Phasenraum bei festgenagelter Energiesumme E. Die inhomogenen wie die homogenen Makrozustände des Beispiels sind dann Abbilder von Teilmengen desselben mikrokanonischen Ensembles, denn die Energie ist konstant. Beispielsweise definiert eine Regel der Art "90% der Atome in der rechten Hälfte" Nebenbedingungen für die Atomkoordinaten, sie bestimmt also eine Teilmenge der homogen erlaubten Phasenschale. Das Phasenvolumen v(E) des homogenen Zustands wird in allen Fällen viele Größenordungen höher als das des inhomogenen. Genauso die Entropie. Das ist ein präzises Resultat der Theorie. Natürlich gilt Energieerhaltung, keine äußere Arbeit oder Wärme sei im Spiel.
Anschaulich gesagt, wir orginisieren eine Lotterie zur Ziehung von kompatiblen Mikrozuständen, also von Punkten im Phasenraum. Zustände mit allen Gasmolekülen in einer Ecke oder mit einem heißen und einem kalten Ende sind sehr sehr unwahrscheinlich, verglichen mit dem gleichmäßigen Gemisch. Obwohl die Entmischung energetisch erlaubt ist und wieder auftauchen könnte, wenn ein extremer Zufall den Gasmolekülen seltene Anfangsbedingungen verschafft. Statistisch einmal im Alter des Universums oder in einem ungeheueren Vielfachen davon. Aus dem gleichen Grund wartet man vergebens darauf, dass ein im Tee verteilter Tropfen Milch sich wieder zusammenballt.
Bei extrem seltenen Makro-Konfigurationen ist der Phasenraum klein und S startet bei minimalen Werten. Mit der Zeit wird ein isoliertes System in immer häufigeren Zuständen angetroffen, S und v(E) sind monoton wachsende Funktionen der Zeit. Das Gebilde zeigt immer weniger Struktur, weshalb die Entropie auch als ein Maß der "Unordnung" gilt.
Beim Urknall war das Universum total unwahrscheinlich, sozusagen physikalisch unmöglich. Und doch war es da. Es war ein "weißes Loch" in einem Zustand sehr kleiner Entropie. Die Entwicklung des Weltalls ist eine ständige Entropieproduktion. Die Schwarzen Löcher sind die Abfallprodukte mit extrem hoher Entropie. Dazwischen gibt es Sonnensysteme mit kontrolliert anschwellender Entropie. Lebewesen wie unsereins können nur existieren als dissipative Strukturen in einer Umgebung, die lange Zeit quasi-stationär neue Entropie produziert. Wir haben Abwehrmechanismen, um die Alterung, das Eindringen von Entropie also, relativ weit zu verzögern.
Einfach zusammengefasst, ist die Entropie gleich dem Logarithmus der Zahl von Möglichkeiten, einen gegebenen makroskopischen Zustand mikroskopisch zu bauen. Makroskopisch heißt, das Objekt ist nur oberflächlich bekannt, nur ein paar pauschale Parameter sind gemessen.
Das erinnert uns an die Abschätzung der Menge von Bits, die man braucht, um einen Brocken von Information zu übertragen. Denn wenn diese Information eine von N möglichen ist, benötigen wir log(N) Bits, wo hier der Logarithmus zur Basis 2 auftritt. Sehr strukturierte und regelmäßige Daten kommen mit weniger Bits aus, sie haben eine kleine Entropie. Chaotische Informationen mit unkenntlichem oder 'unordentlichem' Inhalt haben große Werte der Entropie. Die physikalische und die informationelle Entropie messen beide den Aufwand, der nötig ist, um wirklich alles über einen Gegenstand zu registrieren.
Anhang zu den Differenzialformen[Bearbeiten]
Für Mathematik-Neugierige, kann getrost übersprungen werden. Eine ganze Wissenschaft, für die hier kein Platz ist, betrifft die Formen der Ordnung k auf Mannigfaltigkeiten der Dimension n, sowie deren Operatoren d der "äußeren Ableitung". Die k-Formen sind die natürlichen Integranden auf k-dimensionalen Hyperflächen im n-dimensionalen Raum. Die äußere Ableitung bestimmt, wann eine Form exakt ist (sie ist die Ableitung einer (k-1)-Stammform) und unter welchen topologischen Umständen eine geschlossene Form (äußere Ableitung Null) auch global exakt sein kann, also integrierbar ist.
Dieselbe Art von Ableitung dient auch dazu, die Sätze von Stokes und Green und so weiter zu verallgemeinern, wo die Integrale über das Innere und über die Haut von kartoffeligen Gebilden in Beziehung geraten. Und alle Operationen sind unabhängig vom verwendeten Koordinatensystem, es gelten zwingend eindeutige Umrechnungen von einem ins andere. In ihren beliebten Stilübungen hat die Geometrie die Dinge 'koordinatenfrei' axiomatisiert.
In pingeliger Axiomatik liest sich übrigens sowas wie "dp" nicht mal als "infinitesimale Verschiebung", sondern als die äußere Ableitung der elementaren Koordinatenfunktion p. So wird eine 1-Form ganz eine Formel im Dualraum zum Tangentialraum — explizite Richtungsvektoren denke man sich hinzu.
Bei strengen Beweisführungen hat diese Denkweise Vorteile vor der naiven Lesart als Näherungsformel für kleine Beträge. Die k-Formen sind eigenständige Objekte, keine Approximationen. In der Rechenpraxis fällt die Katze auf ihre Füße und alle Ergebnisse sind gleich. Die Formen besitzen eine Multiplikation und viel Jargon: Sie bilden eine graduierte Grassmann-Algebra, ausgestattet mit dem nilpotenten (Anti-)Derivations-Operator.
Die exakten 1-Formen sind die äußeren Ableitungen von skalarwertigen Funktionen, anders gesagt von den Null-Formen:
- .
Bleiben wir unbeschadet bei der rustikalen Interpretation der 1-Formen, wie sie im 19. Jahrhundert üblich war.
In den drei Raumdimensionen verschleiert sich die Welt der Formen dadurch, dass sie sich alle als Skalarfelder oder Vektorfelder darstellen lassen und ihre Differenzial-Operatoren als Gradient, Rotation, Divergenz. In den vier Dimensionen der relativistischen Raumzeit durchbrechen sie aber den Nebel! Das elektromagnetische Feld F ist eine exakte 2-Form, äußere Ableitung der 1-Form A des Vektorpotenzials: F = dA ⇒ dF = 0.
Existenz der Entropie[Bearbeiten]
Die Herleitung geht von der Tatsache aus, dass keine periodische Maschine bei quasi konstanter Temperatur z.B. die Erdwärme in edle Energie wie Strom verwandelt. Das Perpetuum Mobile zweiter Art ist unmöglich.
Aus der Untersuchung dieses Naturgesetzes, dass kein periodischer Vorgang so einfach die Wärme in Bewegung umsetzt, folgen gleichzeitig die absolute Temperatur und die Zustandsgröße Entropie. Bewundernswert gelang es den gewieften Köpfen (Carnot, Clausius), das qualitative Postulat von der Unmöglichkeit gewisser Maschinen in ein hartes mathematisches Modell zu gießen.
Es gab jede Menge Ansätze, die richtige Temperaturskala zu finden. Fahrenheit, Celsius, Réaumur, wem gebührt bleibender Ruhm? Noch mehr Leute versuchten, ein Perpetuum Mobile zu erfinden. Die dreiste Art der Wundermaschine knackt den Ersten Hauptsatz und schafft neue Energie aus dem Nichts. Die subtilere Art erkennt murrend die Energieerhaltung an, kann aber minderwertige Wärme gleich welcher Temperatur in hochwertige Mechanik umsetzen. Die wissenschaftliche Vernunft schob dem ganzen Zauber einn Riegel vor und behauptete, arrogant aber gender-neutral formuliert:
- Die Erbauer der Perpetuum Mobiles jeglicher Art sind Scharlatane;
- Die Entwicklerinnen von willkürlichen Temperatureinheiten sind Stümperinnen.
Wer ein Mobile erster Art hinbekommt, widerlegt die Existenz der Energie U. Wer eines der zweiten Art patentiert kriegt, widerlegt die Existenz der Entropie S.
Wir betrachten geschlossene Kurven im Zustandsraum des typischen Gaszylinders mit Kolben. Es sollen idealisierte reversible Kreisprozesse sein. Also, es geht langsam. Außendruck und Innendruck beim Austausch von Arbeit, sowie Außentemperatur und Innentemperatur beim Austausch von Wärme, sind stets so gut wie gleich. Die Stücke des Prozesses, in denen nur Arbeit fließt, wobei das Gerät zu 100 Prozent wärmeisoliert ist, heißen adiabatisch. Eine Teilstrecke mit innigem Kontakt zu einem Wärmebad der Temperatur T heißt isotherm; dabei zirkulieren sowohl Arbeit als auch Wärme. Jeder Kreisprozess soll sich beliebig gut als eine Folge von kleinen isothermen und adiabatischen Schritten annähern lassen. Ein theoretischer, idealer Motor soll gebaut werden.
Das Perpetuum-Mobile-Verbot besagt hier, dass Kreisprozesse, die nur eine einzige Außentemperatur zur Verfügung haben, keine Arbeit leisten. Also weder leisten noch aufnehmen, wir verfahren ja reversibel. Die Mobile-Kandidaten dürfen adiabatische Phasen fahren bei den Temperaturen, die sie wollen. Nur wenn Wärme einfließt, sei die Temperatur vorgeschrieben.
Unser Zustandsraum sei eine Ebene mit zwei Koordinaten (P,R) oder alternativ (V,R). Dabei bezeichnet R eine vorläufige Temperatur, sei sie nach Fahrenheit oder sonst wem gemessen. P ist der Druck und V das Volumen. Die drei Größen haben eine Zustandsgleichung f(P,V,R)=0, wahlweise nach P oder V aufzulösen.
Ein elementarer viereckiger Kreisprozess, die Carnot-Maschine, läuft so ab:
- 1. Isotherme Ausdehnung (V1,R1) → (V2,R1) bei der höheren Temperatur R1.
- 2. Adiabatisch weitere Dehnung → (V3,R2) zu niedrigerer Temperatur R2.
- 3. Isotherme Kompression (V3,R2) → (V4,R2) bei kalter Temperatur R2.
- 4. Adiabatische Stauchung-mit-Aufheizung zurück zum Ausgangspunkt (V1,R1).
Bei 1 wird Wärme Q1 aufgesaugt und bei 3 wird Wärme Q3 abgegeben. Bei 1 und 2 wird Arbeit gewonnen, Schritte 3 und 4 fordern Arbeit zurück. Die Bilanz der Arbeit ist A = Q1 - Q3, der Wirkungsgrad ist A/Q1. Wäre die Abwärme Q3 gleich Null, hätten wir ein verbotenes Mobile. Alle Schritte werden idealisiert reversibel durchgeführt.
Behauptung. Alle Carnot-Maschinen zwischen den Temperaturen (R1,R2) arbeiten mit dem gleichen Verhältnis Q3/Q1. Denn angenommen, eine bessere Maschine kann mit der gleichen Abwärme ein größeres Q1' absaugen, also auch mehr Arbeit leisten. Wir koppeln beide und lassen den schlechten Motor rückwärts laufen. Wir ernten eine Netto-Arbeit mit (Q1' - Q1), während bei der niedrigen Temperatur keine Netto-Wärme nach außen fließt. Widerspruch zum Mobile-Verbot.
Jetzt eichen wir die Temperaturmessung um. Statt R nehmen wir die monoton steigende Funktion T(R), so dass das Carnot-Verhältnis auch das Verhältnis der aufgemotzten Temperaturen ist: Q3/Q1 = T(R2)/T(R1).
Der Carnot'sche Wirkungsgrad ist 1 - Q3/Q1 = (T1 - T2)/T1. Mehr geht nicht. Ein Kühler bei T2= 300 Kelvin und ein Feuer bei T1= 600 Kelvin könnten idealerweise 50 % der Wärme verwerten.
Warum fügen die neuen Temperaturen sich nahtlos zusammen? Man nehme drei Temperaturen 1, 2, 3 und zwei reversible Carnot-Maschinen mit den Wärmebilanzen Q1/Q2 und Q2/Q3. Eine dritte Maschine zwischen 1 und 3 muss die Bilanz Q1/Q3 haben! Sonst wären die drei Motoren kombiniert wieder reif für ein viel zu geniales Patent. Ein Auto etwa, das allein mit Hilfe der warmen Sommerluft den Berg hinauf fährt. Und mit selbstlaufender Klimaanlage, versteht sich. Nicht auszudenken, wie schön es wäre.
Ok, ein unbestimmter Faktor ist in T drin und er wurde historisch falsch gewählt, weil Ludwig Boltzmann zu spät kam. Die richtige Temperatur wäre kT statt T. Sie hätte die Dimension der Energie und die Einheit Kelvin des SI-Systems wäre total überflüssig.
Die Carnot-Maschinen sehen mit der neuen Temperatur so aus, dass die Größe (Q/T), die sie bei hoher Temperatur aufnehmen, gleich ist dem Wert (Q/T), den sie im kalten Bad wieder abschwitzen. Weil sie in den adiabatischen Phasen, wo die Temperatur sich ändert, gar keine Wärme tauschen, gilt: das Kurvenintegral der Differenzialform (δQ / T) über einen Carnot-Zyklus ist Null. Nun sagten wir, jede reversible geschlossene Prozesskurve wird genügend genau mit adiabatischen und isothermen Stückchen nachgezeichnet. Wir kacheln die ganze (V,R)-Ebene mit lauter winzig kleinen Carnot-Vierecken. Dann folgern wir: das Integral von (δQ / T) für den beliebigen Kreisprozess verschwindet. Denn alle Segmente im Inneren der Kachelung heben sich gegenseitig auf, wenn wir die Integrale aller Carnot-Kacheln summieren, welche die Fläche innerhalb der geschlossenen Kurve füllen.
Diesem Text fehlen leider mindestens zwei Figuren. Die erste, die einen Carnot-Zyklus in der Ebene zeigt und eine weitere, die eine allgemeinere geschlossene Prozesskurve mit Carnot-Kacheln (oder dünnen Streifen von solchen Mini-Maschinen, Variante) approximiert. Ein Carnot'scher Motor aus dem Bilderbuch wird mit dem idealen Gas betrieben, weil sich dafür die Kurven der Isothermen und Adiabaten leicht berechnen und zeichnen lassen. Die Errungenschaften am Ende der Diskussion, die zwei Größen T,S nämlich, sollen aber allgemein gelten.
Eine 1-Form, deren Integrale über alle geschlossenen Wege verschwindet, ist exakt. Sie besitzt eine Stammfunktion. Angewandt auf die Form (δQ / T) folgt aus der Carnot'schen Analyse: Es existiert eine Stammfunktion S so dass dS = δQ / T. Wir nennen diese Stammfunktion die Entropie und schreiben den Ersten Hauptsatz:
- dU = δA + T dS.
Wie so üblich bei Stammfunktionen, kennen wir S bis auf eine additive Konstante.
Das Paar von Systemvariablen T (intensiv, die absolute Temperatur) und S (extensiv, die Entropie) ist damit etabliert.
Wer das Argument mit den Carnot-Kacheln nicht mag, kann vielleicht mathematisch strenger durch den Grenzübergang an einen Carnot-Viereck zeigen, dass die 1-Form (δQ/T(R)) geschlossen ist, ihre äußere Ableitung verschwindet. Nach einem Lemma von Poincaré sind die geschlossenen Formen exakt, also integrierbar, zumindest in sternförmigen Gebieten. (Das Lemma gilt in allen Dimensionen und für alle Grade von Formen).
Aenderung der Entropie in abgeschlossenen Systemen[Bearbeiten]
Die Entropie wurde entdeckt an Hand von reversibel geführten Abläufen in Systemen, die ihre Energie sowohl als Wärme wie als Arbeit mit der Außenwelt austauschen. Das Modell des Prozesses ist eine Kurve in einem Raum von Zustandsvariablen.
Bei einem reversiblen Prozess zwischen zwei Zuständen ist neben der Energiebilanz eine andere Zahl unabhängig vom Weg im Zustandsraum.
- Nicht die Summe der Wärmeenergie, die getauscht wird;
- Sondern die Summe der geflossenen Wärmen geteilt durch die absoluten Temperaturen.
Diese Größe ist daher eine Zustandsvariable S des Systems, genannt seine Entropie. Ihre Existenz ist äquivalent zur Aussage, dass keine Perpetuum Mobiles (Typ 2) möglich sind.
Sofort kommt die Frage nach irreversiblen Prozessen. Wird das System von der Außenwelt abgekoppelt, verschwinden also alle Variationen von U, A und Q, kann dann sein S irreversible Sprünge machen? Reversibel darf die Entropie nur wandern, wenn Wärme fließt, aber dürfte sie irreversibel hüpfen auch daohne?
Wir nehmen an, das isolierte System habe eine Spezialmechanik, die seinen Zustand in Richtung abnehmender Entropie verändert:
- dU=0, δA=0, δQ=0, δS < 0.
Selbstverständlich respektiert das den 1. Hauptsatz. Dann koppeln wir das System an Wärmebäder und drückende Kolben und organisieren einen reversiblen Schritt, bei dem U konstant bleibt, aber S wieder auf den Anfangswert steigt. Das System nimmt Wärme auf, gleich dem Integral von (T dS), und es produziert damit mechanische Arbeit. Es ist wieder am Ausgangszustand.
Wir isolieren den Apparat und schaffen erneut die Dosis Entropie weg mit unserem speziellen Knopf. So entsteht eine zyklische Maschine, die im Grenzfall kleiner Temperatursprünge mit einem einzigen Wärmebad Arbeit leistet. Ein verbotenenes Mobile ist fertig!?
Daraus folgt schon der Zweite Hauptsatz: in einem abgeschlossenen System kann die Entropie nicht abnehmen. Dann und nur dann, wenn im isolierten System die Entropie wächst, liegt ein irreversibler Vorgang vor.
Der reversible Arbeitsgewinn bei U=const? Angenommen, das System habe eine Zustandsgleichung. Es ist zu Hause auf einer zweidimensionalen Fläche im dreidimensionalen Raum (p,V,T), und wegen U(p,V,T)=const genauer auf einer Kurve in der Fläche. Hat der spontane Entropiesturz uns von Punkt A nach Punkt B geworfen, dann fahren wir kontrolliert auf der Kurve nach A zurück, indem wir die Temperatur T des Wärmebades und den Druck p am Kolben, der die Arbeit aufnimmt, synchron steuern.
Besser aber wäre die strenge Mobile-Strategie mit nur einer Temperatur des Wärmetauschers. Macht der Sturz von A nach B einen Temperaturanstieg, dann geht die reversible Rückführung mit einem einzigen Wärmebad leicht. Erst adiabatische Ausdehnung, also S=const, Arbeitsgewinn bei Abkühlung zur Anfangstemperatur. Dann isothermer Arbeitsgewinn, wobei aus dem Heizbad alle Energie kommt, sowohl für diese Ausdehnung wie für die vorherige adiabatische Arbeit.
Fällt die Temperatur beim geheimnisvollen Schritt von A nach B, müssen wir leider erst adiabatisch arbeiten und das Zeug hin zur Solltemperatur zusammenpressen. Dann isotherm Arbeit gewinnen. Die Arbeitsbilanz ist positiv, mit nur einer Bad-Temperatur. Denn sie gleicht der Wärme, die wir aufsaugen müssen, um S reversibel zu erhöhen. Die vorgeschriebene Bilanz von U ist Null, aber unterwegs haben wir dem U hier Ausflüge erlaubt.
Beim idealen Gas gilt U(p,V,T) = U(T), wie im nächsten Abschnitt drankommt. Daher sind die isothermen Hyperbeln pV = NkT Kurven konstanter Energie U. Der ganze Zyklus läuft bei konstanter Temperatur T. Wir wählen die Richtung mit wachsendem V, um Arbeit zu leisten und Wärme aus dem Bad zu saugen. Das ideale Gas würde das sauberste, einfachste Perpetuum Mobile erlauben. Der mysteriöse Schritt im abgekapselten Zustand wäre eine spontane Kontraktion des Gases, wo es einfach so beschließt, sich mit weniger Volumen zu begnügen. Es meidet dabei alle Außenkontakte, verdächtig wie der Zauberer, der seinen Hut zudeckt, bevor er das Kaninchen herausholt.
Kurz zusammengefasst: Aus dem Mobile-Typ-2-Verbot folgen gleich drei Dinge. Die absolute Temperatur, die Entropie und der Zweite Hauptsatz.
Rechenbeispiel zur Entropie[Bearbeiten]
Folgende Annahmen werden gemacht. Das gas-artige Modellsystem hat bei einer festglegten Zahl von Molekülen eine Zustandsgleichgung für sein Volumen als Funktion von Druck und Temperatur. V=V(p,T). Das ideale Gasgesetz ist das einfachste Spielzeug dieser Art. Wir rechnen in der Ebene der zwei unabhängigen Variablen (p,T).
Der Erste Hauptsatz dU = δA + δQ wird folgendermaßen interpretiert, was die Arbeit bei einem reversiblen Vorgang angeht: Abgegebene Arbeit ist ein anschwellendes Volumen (dV) gegen einen vorhandenen Druck p. Arbeit als Kraft mal Weg ist gleichwertig mit Druck mal Volumen. Das System verliert also innere Energie mit einem Term δA = -p·dV. Eine voll bekannte Differenzialform, darin ist p unabhängige Variable und dV(p,T; dp,dT) kann mit partiellen Ableitungen der Zustandsgleichung als Linearform in (dp,dT) entwickelt werden.
Nun schlägt das Entropie-Postulat zu. Auch der Wärmeterm, bei Abspaltung der anderen unabhängigen Variablen T, kann in der Form δQ = T·dS auftreten, mit einer gewissen Zustandsfunktion S(p,T). Insgesamt gilt symmetrisch
- dU = -p·dV + T·dS.
Der Faktor T ist der wünschenswerte Gegenspieler zum Faktor p im Arbeitsterm.
Benutzen wir kurzzeitig eine tippfaule Notierung für partielle Ableitungen. Für z = z(x,y) nämlich z.x := (∂z/∂x). Die Vertauschbarkeit der Ableitungen besagt: z.x.y = z.y.x. In der Gleichung dU = -p dV + T dS mit unabhängigen Variablen (p,T) nehmen wir an, die Funktion V(p,T) sei eine bekannte Zustandsgleichung. Welche Folgen hat es für U(p,T) und S(p,T)?
Die zwei Faktoren von dU als Linearform von (dp,dT) sind:
- U.p = -p V.p + T S.p ⇒ S.p = (U.p + p V.p) / T
- U.T = -p V.T + T S.T ⇒ S.T = (U.T + p V.T) / T
Die Integrabilität S.p.T = S.T.p etc. ergibt nach kurzer Rechnerei
- U.p = -p V.p - T V.T und S.p = -V.T.
Die p-Ableitungen von U und S sind Ausdrücke in V und dessen Ableitungen. Daher in Integralform:
Wertet man damit die Gleichung von U.T aus, fällt nach leicht umständlicher Rechnung alle p-Abhängigkeit weg und es bleibt die Gleichung für die Funktionen von T in Kleinbuchstaben:
- u'(T) - T·s'(T) = 0.
Im Prinzip kann mit jedem V(p,T) angefangen die Integration von U.p und von S.p erfolgen, dann die Integration von s mit irgendwie erratenem u(T). Die Zustandsgleichung allein bestimmt nicht eindeutig die Systemfunktionen U und S.
Man kann ein beliebiges u(T) vorgeben; diese Funktion meint die Energie im Grenzfall Druck=Null. u'(T) ist die Wärmekapazität als Funktion der Temperatur, bei konstantem Druck. Dann ergibt die Integration von s' = u'/T die Funktion s(T).
Vorsicht! Schlamperei war hier, u'(T) = Cp(T) gleichzusetzen. Denn der Zuwachs der Energie ist genauer einkommende Wärme minus Arbeit durch Ausdehnung. Besser fangen die Integrale statt bei Null bei einem positiven, realistischen Bezugsdruck p=p0 an. Dann bekommen u(T), s(T) richtiger, allgemeiner, die Gleichung
- T·s'(T) = u'(T) + p0·V.T =: Cp ⇒ s'(T) = Cp / T.
Mehr zur Definition von Cp steht im nächsten Abschnitt.
Fazit: Eine Zustandsgleichung allein ist unvollständig und sie begründet auch nicht, wieso die Entropie hereinspaziert. Man braucht zusätzliche Daten zur Wärmekapazität der Substanz. Und das Mobile-Typ-2-Verbot.
Alternative Version. Statt des Druckes benutzen wir das Volumen als die unabhängige Variable. Es gibt die drei Systemfunktionen U(V,T), p(V,T), S(V,T).
Der Erste Hauptsatz hat die gleiche Form dU = -p dV + T dS, nur ist dV bereits das elementare Differenzial einer Koordinate und p = p(V,T). Die Koeffizienten von dV und dT sind
- U.V = -p + T·S.V
- U.T = T·S.T
Aus der Vertauschbarkeit partieller Ableitungen folgt:
- S.V = p.T und U.V = -p + T·p.T.
Integrale in der Variablen des Volumens, V=W :
Hier ist u'(T) =: Cv(T) die frei wählbare Kurve einer Wärmekapazität bei konstantem Volumen, denn dabei variiert aller Wärmetausch genau die innere Energie.
Wärmekapazität, Ideales Gas[Bearbeiten]
Die Wärmekapazität einer Substanz ist die zugeführte Wärme-Energie ΔQ geteilt durch den Temperaturanstieg ΔT, den sie bewirkt. Kurz und altmodisch, die Kalorien die wir für 1 Grad mehr benötigen. Sie heißt auch die Spezifische Wärme. Der Wert hängt von den Umständen ab. Ist die Materie in einem Kasten vom Volumen V eingepfercht, leistet der Wärmefluss keine Arbeit. Darf sie sich aber ausdehnen gegen einen vorgegebenen Druck p, dann macht die Wärmezufuhr sowohl Arbeit wie auch Erwärmung.
Es gibt zwei Wärmekapazitäten, die bei konstantem Volumen Cv und die bei konstantem Druck Cp. Diese sollte größer sein als jene, weil bei Cp die Wärme ΔQ nur zum Teil als innere Energie endet und daher weniger die Temperatur anhebt.
Fall Eins, konstantes Volumen:
- ΔQ = ΔU = Cv ΔT ; ΔV = 0.
Fall Zwei, konstanter Druck:
- ΔQ = Cp ΔT = ΔU + p ΔV ; Δp = 0.
Angenommen die glatten Funktionen U(p,T) und V(p,T) seien bekannt, also die Energie und die Zustandsgleichung. Wir wollen die Wärmekapazitäten auch als Funktion von (p,T) haben.
Für kleine Variationen verwerten wir die linearen Gleichungen
- ΔU = U.p Δp + U.T ΔT
- ΔV = V.p Δp + V.T ΔT
Dann besteht eine Arithmetik-Übung darin, sowohl für Fall Eins wie Zwei alle Größen mit "Delta" davor rauszuwerfen. Ergebnisse hier:
- Cv = U.T - U.p · V.T / V.p
- Cp = U.T + p · V.T
- Cp - Cv = (p - U.p / V.p) · V.T
- Das ideale Gas.
Die Zustandsgleichung hat den Typ: V(p,T) = k T / p. Der Koeffizient k ist eigentlich Nk. Tun wir so, als habe das Gas nur ein Atom oder besser, wir behanden hier Durchschnittswerte pro Atom.
Die Integranden bei den zwei obigen Versionen der Energie verschwinden:
- p·V.p + T·V.T = 0 ; T·p.T - p = 0.
Das Entropiepostulat hat also zur Folge, dass die Innere Energie des idealen Gases nur von der Temperatur, nicht von Druck oder Volumen abhängt: U(p,T) = U(V,T) = u(T).
- Das billigste Modell ist die konstante Wärmekapazität: u(T) = Cv T.
Hier steht Cv, weil dabei aller Wärmefluss in die innere Energie geht. Was liefern die obigen Formeln der Wärmekapazitäten Cp, Cv?
- Cp = Cv + k.
Für Edelgase trifft Cv = 3k/2 ganz gut, denn die Gastheorie lehrt, dass jeder Freiheitsgrad die kinetische Energie (kT/2) aufnimmt. Die Gase von Molekülen haben Vibrationen und Rotationen — deren Energie beschert ihnen eine größere Wärmekapazität. Allerdings sind solche Bewegungen im Gegensatz zu Translationen quantisiert und können bei niedriger Temperatur einfrieren...
Dass die Energie der idealen Gase nicht vom Druck abhängt, und die der realen Gase nur sehr wenig, bestätigte ein klassischer Versuch von Gay-Lussac. Er sperrte ein Gas wärmeisoliert in einem kleinen Volumen ein, nach Messung der Temperatur. Dann ließ er es in ein größeres Volumen zischen, auch wärmeisoliert, und wartete dass es sich beruhigte. Die Temperatur danach war die gleiche wie davor. U(p,T)=U(p',T) weil weder Arbeit noch Wärme nach außen kam und der Erste Hauptsatz galt.
Die Entropie des Gasmodells wird errechnet mit der allgemeinen Integration des vorigen Abschnitts. In den unabhängigen Variablen (V,T) und mit u'(T) = Cv :
- s'(T)= u'(T)/T = Cv / T ⇒ s(T) = Cv · ln(T)
- S(V,T) = s(T) + ∫(k/V') dV' = Cv·ln(T/T0) + k·ln(V/V0)
Die additive Integrationskonstante wurde mit den Nennern T0 und V0 in den Logarithmus eingeschleust. Denn in korrektem Lehrmaterial haben die transzendenten Funktionen wie exp, log, sin, cos immer dimensionslose Argumente. Daher ist hier die Entropie an einem Bezugspunkt (p0,T0) zu Null normiert.
Es kann S in die (p,T)-Ebene umgeschrieben werden:
- (p/p0)·(V/V0) = (T/T0) ⇒ ln(p/p0) = ln(T/T0) - ln(V/V0).
- S(p,T) = Cp·ln(T/T0) - k·ln(p/p0).
Hier wurde Cp = Cv + k benutzt.
Je nach Parameterwahl (V oder p) zieht Cv oder Cp in S am Logarithmus der Temperatur ein.
Die Entropie wird hier nicht ausdiskutiert. Die additiven Konstanten müssen Funktionen der Atomzahl werden, damit S additiv wird für zusammengesetze Systeme. Die Entropien inhomogener und homogener Sammel-Systeme sind zu berechnen, die von Mischungen verschiedener chemischer Stoffe usw. Dass S seine Maxima hat im homogenen Gleichgewichtsfall soll deutlich herauskommen.
Maxwellscher Dämon[Bearbeiten]
Der Maxwellsche Dämon ist ein Fabelwesen, das den Zusammenhang zwischen physikalischer Entropie und Information verdeutlicht. Die Parole dieses Dämons lautet: Wissen ist Macht.
Im neunzehnten Jahrhundert hielt man ein mechanisch-deterministisches Modell der Natur für möglich. Sind die Anfangsbedingungen, nämlich Orte und Geschwindigkeiten aller Atome bekannt, dann kann so ein Modell die Zukunft im Prinzip beliebig genau berechnen. Als wäre das alles ein Planetensystem oder ein Satz idealisierter Billardkugeln. Ob dann die Lebewesen, als molekulare Maschinen begriffen, letztendlich keinen Freien Willen haben? Ist die Natur ein Uhrwerk, ein Algorithmus ohne Zufallsgenerator?
Der Dämon kennt alle Anfangsdaten und alle Bewegungsgleichungen. Dagegen hat der Mensch im Labor nur wenige Messwerte zur Verfügung. Die Informationslücke zwischen Mensch und Dämon ist reine Unkenntnis und kein fundamentaler Zufall, wie ihn später die Quantentheorie einführte. Die Entropie ist das logarithmische Maß der Unkenntnis. Anders gesagt, sie misst den Informationsvorsprung des Dämons. Solange der Mensch keinen Zugriff auf diesen enormen Datensatz hat, bezeichnet er das Unbekannte, berechtigterweise oder nicht, als "Zufall". Das motiviert wohl den Begriff "Zufallsinformation", der in diesem Buch für die Entropie geprägt wurde.
Als Alleswisser kann der Dämon den Zweiten Hauptsatz verletzen. Er bedient zum Beispiel ohne Energieaufwand eine molekulare Klappe zwischen zwei Gefäßen, so dass eines luftleer gepumpt und das andere mit Druckluft von zwei Atmosphären gefüllt wird. Die Entropie sinkt massiv. Zur Erinnerung, sie ist ein Logarithmus der Zahl der mikroskopischen Zustände, die den gleichen Makrozustand ergeben. Proportional zu der Länge in Bits der Daten des Dämons, minus der (lächerlich geringen) Länge in Bits der zugänglichen Labordaten.
Die nötige Bitlänge, um ein Dokument möglichst sparsam zu speichern, ist das Shannon-Maß der Information. Mit der Boltzmann-Konstanten malgenommen, deren Einheit Joule/Kelvin hier eingeht, wird daraus die physikalische Entropie. Hätte man von Anfang an gewusst, dass die absolute Temperatur das Maß für die mittlere Energie eines Freiheitsgrades ist, dann wäre die Entropie dimensionslos wie in der Nachrichtentechnik.
Hat die Entropie subjektive Züge? Wenn mit fortschreitender Technik immer mehr und genauere Messdaten von einen Gegenstand vorliegen, dann hat dieses bessere Objektmodell eine kleinere Entropie als die grobe Beschreibung vorher. Die Entropie hängt ab von der Zahl und der Präzision der gemessenen Parameter. Der Dämon beherrscht den Extremfall, für ihn ist die Entropie immer Null. Er kennt das Wort Zufall gar nicht. Dank des vollständigen Informationsstands des Dämons ist kein Vorgang irreversibel. Er baut Perpetuum Mobiles, die nur den unwissenden Menschen verboten sind. Gewinnt im Lotto, räumt an der Börse ab,...
Die Lehrsätze der Quantenmechanik jagten radikal den Dämon zum Teufel. Ein unberechenbarer, nicht-lokaler Zufallsmechanismus, der "Kollaps der Wellenfunktion", musste nämlich herhalten, um die Statistik selbst von 'verschränkten' Ereignissen richtig zu reproduzieren. Alternativ versuchte eine Viele-Welten-Interpretation die Wellenfunktion stetig zu erhalten. Dann müsste sich aber die Natur fortlaufend in unendlich viele neue Zweige aufspalten, von denen nur einer uns bewusst bliebe. Eine andere Ausrede war, wir haben doch gar kein Modell der Natur, nur Modelle von unserer Wahrnehmung; unsere angehäufte Information macht Sprünge. Die neue Physik hinterließ ein ungutes Bauchgefühl. Niemand konnte sie so erzählen, dass sie restlos überzeugte. Berechnen jedoch ließ sich vieles, mit großartiger Präzision. Das pragmatische Motto: Shut up and calculate.
Zwischen dem dämonischen Hyper-Determinismus und der 'Kollapsologie' alias Kopenhagener Deutung, liegt da Raum für gute Ideen? Eine wurde experimentell widerlegt, Einsteins Hoffnung auf einen "lokalen Realismus". Entfernte Ereignisse haben Koinzidenzen, die vorsichtig gesagt, schneller als das Licht ausgehandelt werden müssten (Nobelpreis an A.Aspect). Diese spukhafte Fernwirkung ist zu unserer Beruhigung jedoch zu wenig, um Energie, Signale, Daten, kausale Auswirkungen zu übertragen. Formal folgt sie zwingend aus dem Kollaps-Algorithmus für verschränkte Wellenfunktionen.
Anhang, Zufall in der Physik[Bearbeiten]
Quantenzufall und Wahrscheinlichkeitslehre im Konflikt[Bearbeiten]
In traditioneller Stochastik gibt es eine Menge M elementarer Ereignisse, einen Wahrscheinlichkeitsraum. All seine 'gutartigen' Teilmengen haben ein positives Maß. Jede messbare Größe alias Zufallsvariable ist eine reellwertige Funktion auf M. Nimmt man an, dass die Quantenzustände Teilmengen von M definieren und dass jedes Orthogonalsystem von Zuständen auf das Werte-Spektrum einer Zufallsvariablen abzubilden ist (Teilmengen des gesuchten Raumes M, die zu orthogonalen Zuständen gehören, haben leeren Durchschnitt), ergibt sich ein Widerspruch. Nachdem gewisse Folgen solcher Funktionen (=Observablen) gegeben sind, werden die weiteren mehrdeutig, unlösbar (Bell-Kochen-Specker). Je genauer der Ort eines Teilchens gemessen wird, umso weniger wird seine Geschwindigkeit definierbar, und umgekehrt (Heisenberg).
Es wurde insbesondere ausprobiert, ob die Heisenbergsche Unbestimmtheit mit einer feineren Definition vom Systemzustand umgangen werden kann. Jede Observable sollte wie gehabt ein Eigenwertspektrum und ein zugeordnetes Orthonormalsystem (ONS) von Eigenzuständen haben. Es ginge nicht darum, die Quantentheorie zu verändern sondern zu "ergänzen". Sie wäre unvollständig, meinte Einstein. Die Natur würfelt da nach einer Bornschen Regel, als Dogma hinzunehmen und bar jeder grundlegenden Herleitung.
Das 'feinere' System soll für jede Observable einen definierten Messwert haben, also in jedem der ONS, Basis zum Eigenwertspektrum einer Variablen, zu genau einem Zustand gehören. Zur formalen Darstellung des vermuteten Mikro-Zustands dient eine Auswahl-Funktion, die in jedem ONS genau ein Element mit 1 bewertet, die anderen mit 0.
Mathematische Beispiele widerlegen die Existenz von Auswahlfunktionen. Eine der einfachsten Kombinationen: ein Netz aus 9 ONS der Größe 4, wobei jeder von 18 Zuständen in genau 2 ONS liegt. Der Vektorraum hat also die Dimension Vier. Die Wertetabelle hat 9 Spalten. In jeder steht genau eine 1, Summe gleich 9. Andererseits ist jeder Zustand, der eine 1 trägt, in genau 2 Spalten vertreten, die Summe ist gerade. Widerspruch.
Observable nach den Regeln der Quantentheorie können keine Funktionen auf einer messbaren Menge sein. Es gibt keine versteckten Variablen, die es erlauben würden, die Quantenzustände in fundamentalere Mikrozustände aufzufächern, welche ein klassisches Wahrscheinlichkeitsmaß besitzen.
Mathematisch fußt die Wahrscheinlichkeitslehre auf den Kolmogorov-Axiomen, die Quantenmechanik auf Von-Neumann-Axiomen. Die zwei Axiomensysteme sind nicht kompatibel und das erklärt zum großen Teil die Irritation über die Physik, also über die Natur im mikroskopischen Bereich.
Spukhafte Fernwirkung, Erklärungsversuch ohne Formeln[Bearbeiten]
Ein Stein des Anstoßes für Albert Einstein war die Vorhersage der Quantenmechanik, dass Phänomene in (beliebig großer) Entfernung eine Wechselwirkung haben sollen, obwohl selbst mit Lichtgeschwindigkeit sich kein Signal von dem einen zum anderen Raum-Zeit-Punkt bewegen kann. Es folgt eine grobe Erläuterung, wie mit statistischer Analyse und mit technischem Aufwand diese Fernwirkung bestätigt wurde.
Es gibt banale Koinzidenzen, um die es hier nicht geht. Wenn jemand wutentbrannt zwei Schuhe in die Menge wirft, in entgegengesetzte Richtungen, dann weiß das Opfer des linken Schuhs, dass woanders der rechte aufschlägt. Die Endpunkte sind passiv, die Korrelation ist 100%.
Statt der Schuhe haben wir mikroskopische Paare von Teilchen, die am Ursprung U gleichzeitig und stark gekoppelt (verschränkt) erzeugt werden. Alice und Bob in recht großer Entfernung fangen je eines der Partikel und sortieren es binär nach verschiedenen Kriterien. Etwa nach Polarisation: horizontal/vertikal, oder links/rechts zirkular, oder links/rechts diagonal. Filter-Apparate und Detektoren arbeiten verlustfrei und sollen blitzschnell umgeschaltet werden, während die Teilchen im Flug sind und sich nichts mehr mit Lichtgeschwindigkeit zuflüstern können. Und Alice und Bob haben ihren freien Willen, sind nicht von einem Dämon ferngesteuert. Beide führen Messreihen durch, ohne sich abzusprechen.
Die plausible Idee des lokalen Realismus sagt nun folgendes. Es gibt ein mathematisches Modell, so dass die Statistiken bei Alice (A) aus den Formeln bei U und denen bei A folgen, die Statistiken bei Bob (B) aus denen bei U und B. Und das Teilchen von Alice hat keine Möglichkeit, von irgendwelchen Manipulationen Bobs beeinflusst zu werden. Die These sagt nichts von Determinismus, sie verbietet nur die Kausalität schneller als das Licht. Die Verteilungsmodelle für die Ereignis-Paare setzen die stochastische Unabhängigkeit der zwei Experimentierenden voraus. Mathematisch ziehen Produkte ein, was A und B als Ursachen betrifft. Bezogen auf Teilmengen von Ereignissen bei B sollten klassische Formeln der bedingten Wahrscheinlichkeit bei A zutreffen.
Wie sieht es nun konkret aus? Alice misst z.B. horizontal-gegen-vertikal. Wenn Bob das auch tut, herrscht 100% Korrelation. Horizontales Ereignis bei B impliziert ebensolches bei A. Messen beide Seiten allgemein mit dem gleichen Drehwinkel der Filter, kommt eindeutig Gleiches heraus. Misst Alice horizontal/vertikal und Bob auf diagonaler Stellung, dann hat sein Ergebnis links/rechts gar keine Aussagekraft für die (50%-50%) Resultate von Alice. Bei 45 Grad Winkelunterschied sind die Statistiken dekorreliert.
Die Theorie beschert uns die Kurvenscharen, Korrelation gegen Filterwinkel. In der Quanten-Version gehören die zwei Teilchen zu einem verschränkten Zustand, einer der nicht einfach ein Produkt ist, ein Faktor pro Teilchen. Die Korrelation kommt aus einem Operator-Produkt, angewandt auf dieses Nicht-Produkt.
Nach der gängigen Kollapsinterpretation verändern Messungen die Zustände. Die Operatoren, die den Messungen bei A und B zugeordnet werden, kommutieren stets, wenn die Ereignis-Punkte raumartig zueinander liegen. Nur ist der verschränkte Zustand nie ein Eigenvektor. Weder des einen noch des anderen Operators. Daher hat der Quanten-Kollaps nach der Messung der einen Variablen nicht-lokale Auswirkungen auf den Zustand beim entfernten Raumzeit-Punkt. Das Quantenmodell ist streng lokal in Bezug auf Operatoren, hat aber verquirlte nichtlokale Zustände. Der lokale Realismus würde es schaffen, dem Modell doch noch solche versteckten Variablen unterzuschieben, die der vorige Abschnitt wegdiskutiert hat.
Die Frage erhob sich, ist das Teilchen bei A autonom? Ereignisse bei B mit gleichem Winkel wie A nageln scheinbar die Sache bei A fest, solche mit schiefem Winkel nicht. Ändert ein Experiment bei Bob schlagartig den Handlungsspielraum des Teilchens von Alice? Oberflächlicher Eindruck? Ein Kalkül der bedingten Wahrscheinlichkeit wischt ihn weg? Oder echtes Problem von Ursache-Wirkung schneller als Licht? Nur mit den Ergebnissen bei 0 und 45 Grad war es unentscheidbar.
Der Forscher John Bell analysierte geschickt die zu erwartende Statistik nach solchen Experimenten, die Häufigkeitsverteilungen der Paare von Teilchen als Funktion der Filterwinkel auf beiden Seiten. Er fand algebraische Kombinationen aus den Korrelationen, die in allen lokal-realistischen Modellen negativ sein müssen, dagegen im Quantenmodell massiv positiv. Mehr als nur zwei Winkel müssen dafür probiert werden. Mit den Bellschen Ungleichungen lagen handfeste Zahlen vor und warteten auf den experimentellen Test. Statt des oberflächlichen Eindrucks eine quantitative Urteilsbegründung. (Man munkelt, Bell habe insgeheim eine Niederlage der Quantenmechanik erhofft.)
Die Versuche bestätigten genau die Quantentheorie, nachdem die technischen Voraussetzungen wie die Schnellwechsel der Filter und der Fang der Photonen ohne nennenswerten Verlust da waren. In der Tat müssen also die Ereignisse bei Alice eine gewisse Abhängigkeit haben von den Knöpfen, die Bob im letzten Moment dreht. Oder umgekehrt, wenn Alice als Erste ihr Filter wählt und ihr ein Photon ins Netz fällt, kommt Bobs Teilchen in Zugzwang, auch wenn es weit weg flog. Die Natur funktioniert nicht streng lokal mit Höchstgeschwindigkeit der Beeinflussung. Theorien mit Einsteins Anforderungskatalog sind falsch.
Der springende Punkt: Alice kann aus ihren Daten allein gar nicht ersehen, ob Bob auf der anderen Seite überhaupt manipuliert und umlenkt oder ob das andere Teilchen ins unendliche Weltall entweicht. Die erste Teil-Annahme der Lokalität bleibt wahr: die Statistik von A hängt von U und A ab. Der Wurm steckt in der Korrelation. Erst nachträglich beim Vergleich der zwei Datensätze findet man gehäuft die Koinzidenzen, die mehr sind als solche, die ein 'lichtkegel-kausales' statistisches Modell erlaubt. Der gegenseite Einfluss geht nicht soweit, dass sich ein Signal schneller als das Licht ausbreiten könnte. Ein Hindernis, das dem Teilchen B plötzlich in den Weg kommt, etwa eine bestimmte Art von Kristall, zerrt also am eigentlich unerreichbaren Teilchen A herum, ohne dass es irgendwem auffällt. Photon A und B waren in der Vergangenheit in eine Partnerschaft verwickelt, die eine unmerkliche, schwache Version von 'Telepathie' zur Folge hat.