Linearisierung von resistiven Sensoren/ Heissleiter
Nehmen wir an, wir wollen mit dem Heißleiter NTCLE100E3 eine analoge Schaltung aufbauen, welche eine zur Temperatur proportionale Ausgangsspannung hat.
Formel[Bearbeiten]
Im Datenblatt[1] finden sich folgende Formeln:
- :
sowie die zugehörigen Konstanten.
Schaltung[Bearbeiten]

Der Logarithmus erscheint im ersten Moment sehr unhandlich, jedoch existiert eine Operationsverstärkerschaltung, welche logarithmieren kann. Die Formel der nebenstehenden Schaltung ist:
wobei:
n und m sind im Wesentlichen von der Diode abhängig. Da sich diese nicht im Datenblatt findet, müssen sie Messtechnisch bestimmt werden.
Zu unserem Zwecke setzen wir zusätzlich die Eingangsspannung konstant:
Der Widerstand R ist unser NTC-Widerstand.
Herleitung[Bearbeiten]
Wir haben diese beiden Formeln:
Als erstes vereinfachen wir die Formel für den Widerstand, indem wir für eine erste Näherung die Anteile höherer Ordnung vernachlässigen:
Nun setzen wir für in der Formel des Logarithmierers ein:
Da können wir A vernachlässigen:
Wir können also schreiben:
In Worten: ist näherungsweise proportional zur Temperatur.
Die Beweisführung ist nicht hieb- und stichfest: Da wir mehrere Variablen weggelassen haben, werden wir später entsprechende Nicht-Linearitäten in der Kennlinie haben.
Schaltung[Bearbeiten]
Die Herleitung beweist nur, dass unsere Schaltung funktioniert, wenn die Variablen wirklich vernachlässigt werden können. Ob dies der Fall ist, soll uns eine Simulation zeigen.
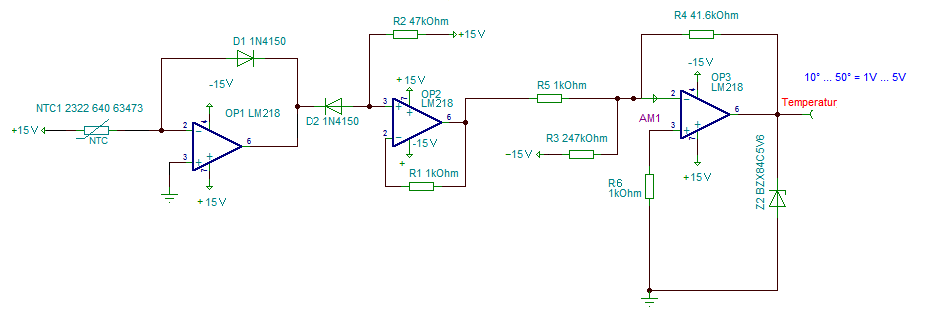
Der in der Schaltung eingebaute Logarithmierer ist temperatur-kompensiert. Die Temperaturkompensation ist bei einer Temperaturmessung zwingend notwendig. Zur Vertiefung: Linearisierung von resistiven Sensoren/ Heissleiter/ Logarithmierer
Gain-Offset-Korrektur[Bearbeiten]
Die Ausgangsfunktion ist näherungsweise linear, ist aber gegenüber der Nulllinie verschoben und besitzt noch die falsche Steilheit.
Verstärkung[Bearbeiten]
Zur Korrektur der Funktion kommt ein Invertierender Addierer zum Einsatz:
Als nächstes muss der Bereich der Ausgangsspannung festgelegt und gemessen werden:
ist die Ausgangsspannung bei tiefster Temperatur und Ausgangsspannung bei höchster Temperatur.
Da beide Funktionen Geraden sind (oder zumindest sein sollen), ist die Verstärkung konstant:
Die Differenz ausschreiben:
Mit der Formel für den invertieren Verstärker, können wir (in einem sinnvollen Rahmen) willkürlich festlegen und berechnen:
Offset[Bearbeiten]
Das Ausgangssignal ist nun linear und hat nun die richtige Steilheit. Jetzt müssen wir nur noch den Offset (Verschiebung gegenüber der Nulllinie) abgleichen.
Hierzu verwende ich den Knotensatz:
ist gegeben durch
da , weil der Knotenpunkt K1 ein virtueller Nullpunkt ist.
ist gegeben durch
Es fehlt uns also nur noch , welchen wir nun mittels Knotensatz bestimmen können:
da auch gilt
haben wir nun alle benötigten Gleichungen.
Da konstante Spannung leichter zu erzeugen ist als konstante Ströme, ist es sinnvoll, die Formel nach dem Widerstand aufzulösen:
Das Ganze rechnen wir noch beim Arbeitspunkt der niedrigsten Temperatur (Bei wäre die Rechnung eben so möglich und käme zum selben Resultat.)
Resultat[Bearbeiten]
(Abweichung der Kennlinie)
(Diskussion und weiteres Vorgehen)
Quellen[Bearbeiten]