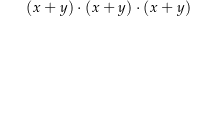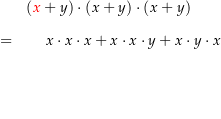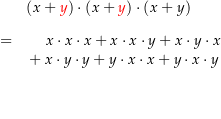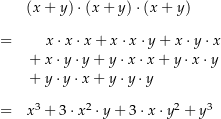Binomischer Lehrsatz – Serlo „Mathe für Nicht-Freaks“
Der binomische Lehrsatz[Bearbeiten]
Sicherlich sind dir die binomischen Formeln noch aus der Schule bekannt. Ich kann mir gut vorstellen, dass dein Mathe-Lehrer sie in seinen Unterrichtsstunden hoch und runter gebetet hat. Nicht ohne Grund! Denn immer wieder helfen sie dir die binomischen Formeln geschickt umzuformen und Beweise einfach zu führen. Hier zur Wiederholung die drei binomischen Formeln, welche für alle gelten:
Denk immer an diese Formeln. Wenn du zum Beispiel auf Terme wie triffst, kannst du sie auch als schreiben. Manchmal kannst du so schwierige Terme vereinfachen oder zusammenfassen. Doch nun zum Thema dieses Kapitels: Wie lauten die binomischen Formeln für größere Potenzen als der 2?. Wir wollen also eine allgemeine Lösungsformel für den Term für finden.
Hinweis
Denk daran, wenn wir wissen, was ist, wissen wir auch, was ist. Denn wir können als schreiben und für können wir die gefundene Formel anwenden. Dies gilt insbesondere auch für die obigen binomischen Formeln. So folgt wegen die zweite binomische Formel direkt aus der ersten.
Schauen wir uns ein Beispiel an: Wir wollen wissen, was ist. Hierzu müssen wir den Term ausmultiplizieren, wie es in der folgenden Animation gezeigt wird:
Wir erhalten so den Term . Es fällt auf, dass für jeden Summanden der Gesamtsumme die Summe der Exponenten von und gleich 3 ist. Dies leuchtet ein. Wir nehmen nämlich, wenn wir das Produkt ausmultiplizieren, aus jedem der Terme entweder ein oder ein (in jeden Summanden kommen insgesamt 3 Faktoren oder vor). Die Summe der Exponenten beider Variablen muss also gleich 3 sein. Es müssen so nur noch die Koeffizienten der einzelnen Summanden bestimmt werden.
Wir sind nun bereit für den allgemeinen Fall. Wir wollen wissen:
Wir wissen, dass das Ergebnis eine Summe von Potenzen in und ist. Die Summe der Exponenten in jedem Summanden ist gleich . Alle Potenzen besitzen also die Form , wobei eine natürliche Zahl ist (die 0 ist mit eingeschlossen). Wir müssen noch die Koeffizienten dieser Potenzen bestimmen. Betrachten wir einige Beispiele. Der Koeffizient von muss 1 sein. Denn wenn wir diese Potenz erhalten wollen, müssen wir aus allen Termen die Variable wählen:
Analog ist auch der Koeffizient für 1. Doch wie lautet allgemein der Koeffizient für den Term ? Dazu müssen wir aus den Termen -mal die Variable und -mal die Variable wählen. Doch wie viele Möglichkeiten gibt es aus Termen -mal eine Variable auszuwählen? Fällt dir etwas auf? Genau, dies ist der im vorherigen Abschnitt diskutierte Binomialkoeffizient ! Dementsprechend ist der Koeffizient von gleich (Deshalb auch der Name: Binomialkoeffizient!). Wir erhalten:
Satz (Der binomische Lehrsatz)
Für alle reellen Zahlen und und für alle natürlichen Zahlen gilt:
Folgerungen aus dem binomischen Lehrsatz[Bearbeiten]
Mit Hilfe des binomischen Lehrsatzes kannst du nun weitere Antworten auf Fragen der Kombinatorik finden. Stell dir vor, du hast eine beliebige, endliche Menge gegeben. Wie viele Teilmengen kannst du aus dieser Menge bilden? Wir wissen bereits, dass die Anzahl der -elementigen Teilmengen von dem Binomialkoeffizienten entspricht ( ist die Anzahl der Elemente der Menge ). Um die Gesamtzahl aller Teilmengen der Menge zu finden, müssen wir die Summe über die Anzahl aller -elementigen Teilmengen von mit bilden. Wir erhalten (Anmerkung: ist Potenzmenge von , also die Menge aller Teilmengen von . Dementsprechend ist die Anzahl aller Teilmengen von .):
Frage: Was ist das Ergebnis der obigen Summe? Vergleiche dazu die obige Summe mit dem binomischen Lehrsatz!
Die obige Summe entsteht aus dem binomischen Lehrsatz für und . Dementsprechend ist .
Satz (Größe der Potenzmenge einer endlichen Menge)
Sei eine beliebige endliche Menge. Dann ist .
Und wie sieht es mit der folgenden Summe aus?
Frage: Wie lautet das Ergebnis der obigen Summe?
Die obige Summe entsteht aus dem binomischen Lehrsatz für und . Das Ergebnis der Summe lautet dementsprechend: