Unstetigkeit beweisen: Epsilon-Delta-Kriterium und Folgenkriterium – Serlo „Mathe für Nicht-Freaks“
Überblick
[Bearbeiten]Um die Unstetigkeit einer Funktion zu beweisen, muss man zeigen, dass diese mindestens eine Unstetigkeitsstelle besitzt. Für den Nachweis einer Unstetigkeitsstelle kann man eine von mehreren Methoden verwenden:
- Folgenkriterium: Man kann nachweisen, dass die Funktion an der betrachteten Stelle das Folgenkriterium nicht erfüllt.
- Betrachtung des links- und rechtsseitigen Grenzwert: Man kann den linksseitigen und rechtsseitigen Grenzwert der Funktion an der betrachteten Stelle ausrechnen. Wenn entweder einer dieser beiden Grenzwerte nicht existiert oder wenn diese Grenzwerte unterschiedlich sind, dann ist die Funktion an der betrachteten Stelle unstetig.
- Epsilon-Delta-Kriterium: Man kann nachweisen, dass die Funktion an der betrachteten Stelle das Epsilon-Delta-Kriterium nicht erfüllt.
Folgenkriterium
[Bearbeiten]→ Hauptartikel: Folgenkriterium der Stetigkeit: Folgenstetigkeit
Wiederholung: Folgenkriterium
[Bearbeiten]Definition (Folgenkriterium der Stetigkeit an einer Stelle)
Eine Funktion mit ist stetig an der Stelle , wenn für alle Folgen mit und gilt:
Beweisskizze
[Bearbeiten]Um mit dem Folgenkriterium zu zeigen, dass eine Funktion an der Stelle unstetig ist, muss man eine Argumentenfolge mit für alle und dem Grenzwert finden, so dass die Funktionswertfolge nicht gegen konvergiert. Es soll also und gelten. Für gibt es zwei Möglichkeiten:
- Die Funktionswertfolge divergiert.
- Die Funktionswertfolge konvergiert, jedoch ist ihr Grenzwert ungleich .
Ein Unstetigkeitsbeweis über das Folgenkriterium könnte zum Beispiel folgende Form aufweisen:
Sei eine Funktion mit . Diese Funktion ist unstetig an der Stelle . Wählen wir nämlich die Folge mit , so liegen alle Folgenglieder im Definitionsbereich von , und wir haben
Jedoch ist . Es ist nämlich ...Beweis, dass divergiert oder dass der Grenzwert von ungleich ist...
Beispielaufgabe
[Bearbeiten]Aufgabe (Unstetigkeit der topologischen Sinusfunktion)
Beweise die Unstetigkeit der folgenden Funktion:
Wie kommt man auf den Beweis? (Unstetigkeit der topologischen Sinusfunktion)
Damit eine unstetige Funktion ist, muss sie mindestens eine Unstetigkeitkeitsstelle besitzen. Für jedes entspricht in einer hinreichend kleinen Umgebung von der Funktion . Da die Funktion als Komposition stetiger Funktionen stetig ist, muss auch für alle stetig sein. Damit muss die Unstetigkeitsstelle bei liegen.
Um mit dem Folgenkriterium zu zeigen, dass an der Stelle unstetig ist, müssen wir eine Argumentenfolge mit und finden. Um diese Argumentenfolge zu finden, schauen wir uns zunächst den Graphen der Funktion an:

In der Graphik sehen wir, dass die Funktion in jeder Umgebung des Nullpunkts jeden Wert zwischen und beliebig oft annimmt. Also können wir so wählen, dass immer gleich ist. Dann ist nämlich garantiert, dass ist. Dabei wählen wir so, dass von oben gegen Null konvergiert.
In der folgenden Graphik sind neben dem Graphen von auch die Funktionswerte der Folge eingetragen. Man sieht, dass für die Funktionswerte gegen konvergieren, was ungleich dem Funktionswert ist:
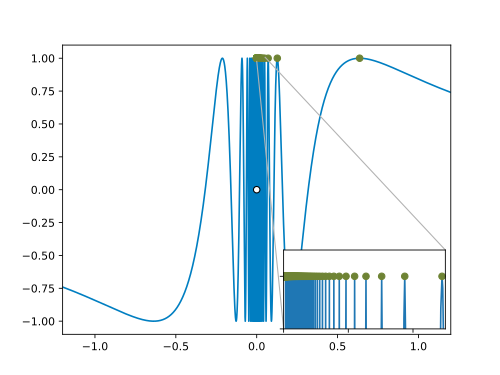
Wie lauten die Werte für ? Formen wir hierzu die Gleichung nach um:
Für alle mit gilt also . Damit unsere Argumente positiv sind und von oben gegen Null konvergieren, wählen wir . Es gilt dann:
Jedoch haben wir gesehen, dass ist. Wir haben also eine Argumentenfolge gefunden, welche die Unstetigkeit von an der Stelle beweist.
Beweis (Unstetigkeit der topologischen Sinusfunktion)
Sei mit für und . Wir betrachten die Folge mit . Für diese Folge ist:
Außerdem gilt:
Damit ist , obwohl ist. Dies beweist, dass an der Stelle und somit auch insgesamt unstetig ist.
Baustelle: Betrachtung des links- und rechtsseitigen Grenzwerts
[Bearbeiten]In diesem Abschnitt sollte man an einem Beispiel einer Funktion mit Fallunterscheidung zeigen, wie man durch die Betrachtung des links- und rechtsseitigen Grenzwerts die Unstetigkeit einer Funktion beweisen. Jedoch sollte zunächst im Kapitel Mathe für Nicht-Freaks: Grenzwert von Funktionen der links- und rechtsseitige Grenzwert eingeführt werden. Auch muss dort bewiesen werden, dass eine Funktion an einem Punkt genau dann stetig ist, wenn der links- und rechtsseitige Grenzwert existiert und dem Funktionswert an einer Stelle entspricht.
Epsilon-Delta-Kriterium
[Bearbeiten]→ Hauptartikel: Epsilon-Delta-Kriterium der Stetigkeit
Wiederholung: Epsilon-Delta-Kriterium
[Bearbeiten]Definition (Epsilon-Delta-Definition der Unstetigkeit)
Eine Funktion mit ist genau dann unstetig an der Stelle , wenn es ein gibt, so dass es für alle ein mit und gibt. ist also genau dann in unstetig, wenn gilt
Allgemeine Beweisstruktur
[Bearbeiten]Epsilon-Delta-Kriterium der Unstetigkeit kann folgendermaßen in Prädikatenlogik formuliert werden:
Daraus ergibt sich ein Schema, mit dem die Unstetigkeit einer Funktion nach dem Epsilon-Delta-Kriterium bewiesen werden kann:
Beispielaufgabe
[Bearbeiten]Aufgabe (Unstetigkeit der topologischen Sinusfunktion)
Beweise die Unstetigkeit der folgenden Funktion an der Stelle :
Wie kommt man auf den Beweis? (Unstetigkeit der topologischen Sinusfunktion)
Bei dieser Aufgabe soll die Unstetigkeit einer Funktion gezeigt werden. Wir betrachten hierzu die Negation des Epsilon-Delta-Kriteriums. Unser Ziel ist es sowohl ein , als auch ein so zu wählen, dass und ist. Dabei darf in Abhänigigkeit von gewählt werden, während unabhängig für alle sein muss. Für eine Lösung können wir folgendermaßen vorgehen:
Schritt 1: Zielungleichungen vereinfachen
Zunächst können wir beide Ungleichungen, die erfüllt sein müssen, umschreiben, denn in unserem Fall ist und . Dadurch können wir schreiben: und .
Schritt 2: Wahl eines geeigneten
Wir betrachten nun den Graphen der Funktion – dieser hilft uns nämlich unsere „Beweisbausteine“ zu finden:

Wir müssen ein finden, so dass es stets Funktionswerte im Bereich gibt, die einen Abstand größer gleich von haben – egal wie klein ist. Sprich: Egal, welches wir wählen, es gibt immer Punkte die oberhalb oder unterhalb des --Rechtecks liegen.
In der Grafik erkennen wir, dass die Funktion in der Nähe des Nullpunkts unendlich oft zwischen und oszilliert. Damit bietet sich ein an. Dann gibt es nämlich immer Funktionswerte in jeder noch so kleinen Umgebung von der Null mit . Wir wählen . In der folgenden Grafik ist dies illustriert:
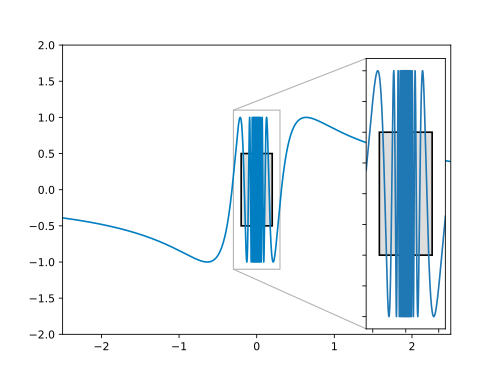
Im Beweis müssen wir nach der Wahl von das beliebig größer Null wählen. Das machen wir dann auch.
Schritt 3: Wahl eines geeigneten
Wir haben gesetzt. Es muss nun gelten . Damit diese Bedingung erfüllt ist, können wir solche mit wählen. Nun ist genau dann, wenn für ein ist. Für die gesuchten gilt also:
Damit haben wir verschiedene gefunden, für die gilt. Jetzt muss noch die erste Bedingung beachtet werden. Unsere hängen von ab. Wir müssen ein geeignetes mit finden, so dass erfüllt ist. Setzen wir also in diese Ungleichung die gefundene Gleichung ein und stellen sie nach um:
Dies liefert den Ausdruck . Wählen wir also eine natürliche Zahl , die größer als ist, so ist erfüllt. Ein solches muss nach dem archimedischen Axiom existieren. Wählen wir ein solches und definieren damit das über , haben wir sowohl als auch gegeben. Damit sind alle Bausteine für den Beweis gefunden und dieser muss nur noch sauber aufgeschrieben werden.
Beweis (Unstetigkeit der topologischen Sinusfunktion)
Wähle und sei beliebig. Wähle eine natürliche Zahl , so dass . Eine solche natürliche Zahl muss nach dem Archimedischen Axiom existieren. Weiter sei . So gilt:
Weiter ist:
Damit ist die Funktion unstetig an der Stelle .
Übungsaufgaben
[Bearbeiten]Epsilon-Delta-Kriterium: Vorzeichenfunktion
[Bearbeiten]Aufgabe (Unstetigkeit der Vorzeichenfunktion)
Beweise, dass die Vorzeichenfunktion mit folgender Zuordnungsvorschrift unstetig ist:
Wie kommt man auf den Beweis? (Unstetigkeit der Vorzeichenfunktion)
Um die Unstetigkeit zu beweisen, müssen wir eine Unstetigkeitsstelle der Funktion finden. Schauen wir uns hierzu den Graphen der Funktion an:

Man sieht, dass die Funktion an der Nullstelle einen Sprung aufweist. Bei sollte sich also eine Unstetigkeitsstelle befinden. Nun müssen wir ein finden, für welches kein gefunden werden kann, so dass die Funktion komplett im --Rechteck liegt. Hier müssen wir kleiner als die Sprunghöhe wählen – zum Beispiel . Egal welches wir nun vorgeben, es muss Funktionswerte unter- oder oberhalb des --Rechtecks geben.
Sei also beliebig. Wir müssen nun zeigen, dass es ein mit und gibt. Schauen wir uns zunächst die Ungleichung an:
Bei der Ungleichung ergibt sich:
Das muss damit so gewählt werden, dass und ist. Beginnen wir mit der zweiten Ungleichung . Für ist entweder oder . Für gilt somit immer .
Blicken wir nun auf die Ungleichung . Wie wir gerade geschlossen haben, soll sein. Dies ist zum Beispiel für alle mit erfüllt. Wählen wir also für den Mittelwert zwischen und mit .
Dies sehen wir auch in folgender Grafik. Hier haben wir das --Rechteck mit und eingetragen. Alle Punkte, die unter- oder oberhalb des Rechtecks liegen, sind rot markiert. Dies sind alle im Intervall mit . Unsere Wahl ist gesondert markiert und liegt oberhalb des Rechtecks:
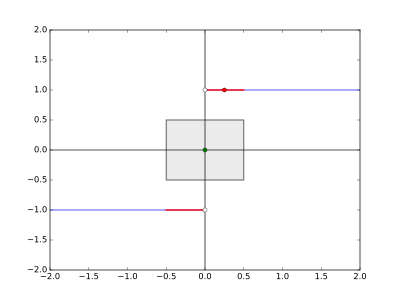
Die Wahl von reicht aus.
Beweis (Unstetigkeit der Vorzeichenfunktion)
Wir setzen . Außerdem wählen wir . Sei beliebig. Wählen wir . Zum einen ist:
Zum anderen ist
Damit ist an der Stelle unstetig und somit insgesamt unstetig.





































![{\displaystyle {\begin{aligned}{\begin{array}{rrrl}&&f(x)&=1\\[0.5em]{\overset {f(0)\neq 0}{\iff {}}}&&\sin \left({\frac {1}{x}}\right)&=1\\[0.5em]\iff {}&\exists k\in \mathbb {Z} :&{\frac {1}{x}}&={\frac {\pi }{2}}+2k\pi \\[0.5em]\iff {}&\exists k\in \mathbb {Z} :&x&={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee2a00a2f43e5e9d665e22fb3757d1c17b30b5e)






![{\displaystyle {\begin{aligned}\lim _{n\to \infty }f(x_{n})&=\lim _{n\to \infty }f\left({\frac {1}{{\frac {\pi }{2}}+2n\pi }}\right)\\[0.5em]&=\lim _{n\to \infty }\sin \left({\frac {1}{\frac {1}{{\frac {\pi }{2}}+2n\pi }}}\right)\\[0.5em]&=\lim _{n\to \infty }\sin \left({\frac {\pi }{2}}+2n\pi \right)\\[0.5em]&=\lim _{n\to \infty }1=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a891cfa8167534da2fbdc7f3ff20d74e618118ce)







![{\displaystyle {\begin{array}{l}{\color {Red}\underbrace {{\underset {}{}}{\text{Wähle }}\epsilon =\ldots } _{\exists \epsilon >0}}\ {\color {RedOrange}\underbrace {{\underset {}{}}{\text{Sei }}\delta >0{\text{ beliebig.}}} _{\forall \delta >0}}\\{\color {OliveGreen}\underbrace {{\underset {}{}}{\text{Wähle }}x=\ldots {\text{ Es ist }}x\in D{\text{, weil}}\ldots } _{\exists x\in D}}\\{\color {Black}{\text{Es ist:}}}\\[0.5em]\quad \quad {\color {DarkOrchid}{\text{Beweis für }}|x-x_{0}|<\delta }\\[0.5em]\quad \quad {\color {Blue}{\text{Beweis für }}|f(x)-f(x_{0})|\geq \epsilon }\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c0c5a3c4e581aa0e948d62d47988aebd61cfe16)





















![{\displaystyle {\begin{aligned}\left|x\right|<\delta &\iff \left|{\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right|<\delta \\[0.5em]&\iff {\frac {1}{{\frac {\pi }{2}}+2k\pi }}<\delta \\[0.5em]&\iff 2k\pi +{\frac {\pi }{2}}>{\frac {1}{\delta }}\\[0.5em]&\iff 2k\pi >{\frac {1}{\delta }}-{\frac {\pi }{2}}\\[0.5em]&\iff k>{\frac {1}{2\pi }}\left({\frac {1}{\delta }}-{\frac {\pi }{2}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25af20f89560c07b3820129dd8d10ce2b902d7e9)


![{\displaystyle {\begin{aligned}k>{\frac {1}{2\pi }}\left({\frac {1}{\delta }}-{\frac {\pi }{2}}\right)&\implies 2k\pi >{\frac {1}{\delta }}-{\frac {\pi }{2}}\\[0.5em]&\implies 2k\pi +{\frac {\pi }{2}}>{\frac {1}{\delta }}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ {\frac {1}{a}}>{\frac {1}{b}}>0\iff 0<a<b\right.}\\[0.5em]&\implies {\frac {1}{{\frac {\pi }{2}}+2k\pi }}<\delta \\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ {\frac {1}{{\frac {\pi }{2}}+2k\pi }}>0\right.}\\[0.5em]&\implies \left|{\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right|<\delta \\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ x={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right.}\\[0.5em]&\implies \left|x\right|<\delta \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad7985a4bd1699ae43466813ef6cb9d56079acd3)
![{\displaystyle {\begin{aligned}\left|f(x)-f(0)\right|&=\left|\sin \left({\frac {1}{x}}\right)-0\right|\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ x={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right.}\\[0.5em]&=\left|\sin \left({\frac {\pi }{2}}+2k\pi \right)\right|\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sin \left({\frac {\pi }{2}}+2k\pi \right)=1\right.}\\[0.5em]&=\left|1\right|\geq {\frac {1}{2}}=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fa308896735c40f86148e2d6dfd09fa66590f03)



![{\displaystyle {\begin{aligned}{\begin{array}{rrl}&|f(x)-f(x_{0})|&\geq \epsilon \\[0.5em]\iff &|\operatorname {sgn}(x)-\operatorname {sgn}(x_{0})|&\geq {\frac {1}{2}}\\[0.5em]\iff &|\operatorname {sgn}(x)-\operatorname {sgn}(0)|&\geq {\frac {1}{2}}\\[0.5em]\iff &|\operatorname {sgn}(x)|&\geq {\frac {1}{2}}\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcc44b40d90ac63c780e7d0dc1f8f767d68457c2)









![{\displaystyle {\begin{aligned}{\begin{array}{rrl}&{\frac {1}{2}}&<1\\[0.5em]\implies &{\frac {1}{2}}\delta &<\delta \\[0.5em]\implies &\left|{\frac {1}{2}}\delta \right|&<\delta \\[0.5em]\implies &\left|{\frac {1}{2}}\delta -0\right|&<\delta \\[0.5em]\implies &|x-x_{0}|&<\delta \end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57e7f87669f9fd77335e50cfd861641e94a2002b)
![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=|\operatorname {sgn}(x)-\operatorname {sgn}(x_{0})|\\[0.5em]&=\left|\operatorname {sgn} \left({\frac {\delta }{2}}\right)-\operatorname {sgn}(0)\right|\\[0.5em]&=\left|1-0\right|\\[0.5em]&=1\\[0.5em]&\geq {\frac {1}{2}}=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3167c8c11ff695bed71173f7068a3da353af4e5)

