Wurzel – Serlo „Mathe für Nicht-Freaks“
Motivation der Wurzel[Bearbeiten]
Die Motivation hinter der Wurzel ist die Umkehrung der Potenzbildung. Zur Wiederholung: Ist eine reelle Zahl, so ist die -te Potenz von definiert als
Die Wurzel ist nun die Antwort auf die Frage: Bei einer gegebenen reellen Zahl erfüllt welche reelle Zahl die Potenzgleichung ? Die -te Wurzel einer Zahl (für die wir später schreiben werden) soll eine Zahl sein, für die gilt.
Probleme bei der Definition der Wurzel[Bearbeiten]

Wenn wir die Lösungen der Potenzgleichung untersuchen, dann stellen wir zwei Probleme fest: Zum einen ist nicht jede Potenzgleichung lösbar und zum anderen kann eine solche Gleichung mehrere Lösungen besitzen.
Nicht jede Potenzgleichung ist lösbar[Bearbeiten]
Nicht jede Potenzgleichung besitzt eine Lösung in den reellen Zahlen. Beispielsweise gibt es keine reelle Zahl , die die Gleichung erfüllt, da stets eine nicht-negative Zahl ist. Generell ist die Potenzgleichung immer dann in den reellen Zahlen unlösbar, wenn eine gerade Zahl und negativ ist. In diesem Fall ist nämlich stets nicht-negativ und kann damit nie gleich der negativen Zahl sein.
Um nun Lösungen der Potenzgleichung für alle finden zu können, werden wir im Folgenden nur nicht-negative Zahlen zulassen. Unter dieser Beschränkung können wir nämlich beweisen, dass die Potenzgleichung mindestens eine Lösung besitzen muss. Bei ungeradem tritt dieses Problem im Übrigen nicht auf, weil dann auch negativ werden kann.
Eine Potenzgleichung kann mehrere Lösungen besitzen[Bearbeiten]
Eine Potenzgleichung kann mehrere Lösungen besitzen. Nimm zum Beispiel die Gleichung , welche die beiden Lösungen und besitzt. Nun soll aber die -te Wurzel einer Zahl eindeutig definiert sein. Welche Lösung der Potenzgleichung wählt man also, wenn es mehrere Lösungen gibt?
Wenn man die Potenzgleichungen untersucht, dann stellt man fest, dass dieses Problem genau dann auftritt, wenn eine gerade Zahl und positiv ist. In diesem Fall gibt es genau zwei Lösungen: eine positive und eine negative Lösung. Hier werden wir die positive Lösung als -te Wurzel wählen. Im Beispiel der Gleichung werden wir die Lösung als Quadratwurzel von wählen. Um auch Null als Wurzel zuzulassen, werden wir deswegen festlegen, dass die Wurzel immer nicht-negativ sein soll.
Zusammenfassung[Bearbeiten]
Wir haben festgelegt, dass in der Gleichung die Zahl zur Bestimmung der Wurzel nicht-negativ sein muss. Auch haben wir bestimmt, dass wir die nicht-negative Lösung dieser Gleichung als Wurzel definieren. Wir werden später mit Hilfe der Vollständigkeit von zeigen, dass unter diesen Voraussetzungen die -te Wurzel einer reellen Zahl immer existiert. Auch werden wir beweisen, dass die Wurzel unter diesen Bedingungen immer eindeutig ist.
Definition[Bearbeiten]
Definition der Wurzel[Bearbeiten]
Wir definieren formal sauber:
Definition (Definition der n-ten Wurzel)
Für ist die -te Wurzel einer nicht-negativen reellen Zahl die nicht-negative reelle Zahl , für die gilt . Wir schreiben an Stelle von dann . Für die Quadratwurzel schreiben wir auch .
Dass die -te Wurzel existiert und eindeutig ist, werden wir später zeigen. Auch werden wir sehen, warum es sinnvoll ist, für eine Wurzel die Potenz aufzuschreiben.
Verständnisfragen: Bestimme folgende Wurzeln:
Antworten:
- ist nicht definiert.
- ist nach unserer Definition nicht definiert.
Die Wurzelfunktion[Bearbeiten]

Mit der Wurzel können wir für die Wurzelfunktion definieren. Sie ist die Umkehrfunktion der Potenzfunktion
Die Wurzelfunktion ist
Hinweis
Da die Potenzfunktion für ungerade Exponenten auch auf den negativen reellen Zahlen umkehrbar ist, wird die Wurzelfunktion für ungerade in der Literatur häufig auf ganz definiert.
Unterscheidung: Wurzel, Wurzelfunktion und Lösung einer Potenzgleichung[Bearbeiten]
Es ist in der Analysis sehr wichtig, unterschiedliche Begriffe voneinander unterscheiden zu können. Drei Begriffe, die oftmals wild durcheinander geworfen werden, sind Wurzel, Wurzelfunktion und Lösung der Potenzgleichung :
- Wurzel
- Die Wurzel ist diejenige nicht-negative reelle Zahl, die die Potenzgleichung für erfüllt. Es handelt sich also bei einer Wurzel um eine reelle Zahl.
- Wurzelfunktion
- Wie der Name es bereits andeutet, handelt es sich bei der Wurzelfunktion um eine Funktion. Diese ist definiert als . Sie ist damit eine Funktion mit den nicht-negativen reellen Zahlen als Definitionsbereich und den nicht-negativen reellen Zahlen als Wertebereich. Dabei ordnet sie einer nicht-negativen Zahl ihre Wurzel zu.
- Lösung der Potenzgleichung
- Die Lösung einer Potenzgleichung ist eine reelle Zahl , die diese Gleichung erfüllt. Nun kann eine Potenzgleichung mehrere Lösungen haben. Wenn eine nicht-negative Zahl ist, dann ist die -te Wurzel von eine dieser Lösungen, muss aber nicht die Einzige sein. Eine Aussage wie „ ist die Lösung der Gleichung “, ist nicht richtig, da nicht die, sondern nur eine der zwei Lösungen und von ist.
Verständnisfragen: Wie müsste die Aussage „ ist die Lösung der Gleichung “ korrekt heißen?
„ ist die positive Lösung der Gleichung “ oder „ ist eine Lösung der Gleichung “
Wurzel als Potenz[Bearbeiten]
Es ist auch üblich, anstelle von die Schreibweise zu benutzen. Die Wurzel wird hier als spezielle Potenz aufgefasst. Dies ergibt Sinn, denn für Wurzeln gelten dieselben Rechenregeln wie für Potenzen mit ganzzahligen Exponenten. Dies werden wir später im Kapitel „Rechenregeln der Wurzel“ untersuchen. Für negative ganzzahlige Potenzen hatten wir gesetzt. Damit sich dies auch mit der Potenzschreibweise für Wurzeln übereinstimmt, definieren wir für alle
Dieser Abschnitt muss noch ausgebaut werden: Warum macht es Sinn zu definieren? -> vielleicht im Abschnitt zu den Rechenregeln der Wurzel ergänzen?! -- Stephan Kulla 22:49, 5. Mai 2016 (CEST) -> Ist mir nicht klar, wie du das meinst?! Die Erklärung, warum es sinnvoll ist "hoch -..." als "eins durch hoch ..." zu setzen, muss vorher, bei Potenzen mit ganzzahligen Exponenten, geschehen! -- Benutzer:who2010 Who2010 17:15, 7. Mai 2016 (CEST)
Eindeutigkeit der Wurzel[Bearbeiten]
Hilfssatz zum Beweis der Eindeutigkeit[Bearbeiten]
Zunächst zeigen wir, dass die -Wurzel eindeutig ist. Dafür benötigen wir den folgenden Hilfssatz:
Satz
Seien und nicht-negative reelle Zahlen mit . Für alle gilt dann .
Beweis
Im Kapitel „Folgerungen der Anordnungsaxiome“ hatten wir gezeigt
Setzen wir nun und , so folgt
Wenden wir diese Formel nun -mal hintereinander an, so gilt
Beweis der Eindeutigkeit[Bearbeiten]
Nun können wir die Eindeutigkeit der Wurzel zeigen:
Satz (Eindeutigkeit der Wurzel)
Sei eine nicht-negative reelle Zahl und eine beliebige natürliche Zahl. So gibt es höchstens eine nicht-negative reelle Zahl mit .
Beweis (Eindeutigkeit der Wurzel)
Wir führen einen Widerspruchsbeweis, indem wir die Aussage „es gibt zwei verschiedene -te Wurzeln von “ auf einen Widerspruch führen. Nehmen wir also an, dass es zwei verschiedene nicht-negative reelle Zahlen und mit und . Da ist, gilt entweder oder .
Betrachten wir nun den Fall . Da ist, folgt mit dem Hilfssatz von oben . Nun ist aber nach Voraussetzung und . Damit erhalten wir den Widerspruch
Damit kann nicht sein. Auch im Fall kommen wir analog zu einem Widerspruch. Dies zeigt, dass es höchstens eine Wurzel von geben kann.
Existenz der Wurzel[Bearbeiten]
Exkurs: Das Dilemma der griechischen Mathematik[Bearbeiten]
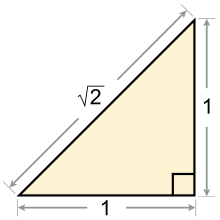

Ich möchte dir nun zeigen, dass die Existenz der Wurzel nicht selbstverständlich ist: Beispielsweise gibt es in der Grundmenge der rationalen Zahlen keine Zahl, die die Potenzgleichung löst. Damit gibt es in den rationalen Zahlen keine Wurzel von .
Bereits den alten Griechen war dies bekannt.
tritt zum Beispiel beim Einheitsquadrat auf, denn es ist die Länge der Diagonale eines Quadrates mit einer Kantenlänge von Maß . Nach dem Satz des Pythagoras über rechtwinklige Dreiecke erhalten wir für die Gleichung . Wenn wir diese nach durch Wurzelziehen umstellen, dann ergibt sich für die Diagonale die Länge . Damit kann auch mit Hilfe von Zirkel und Lineal bestimmt werden:

Wir wollen nun durch einen Widerspruchsbeweis zeigen, dass keine rationale Zahl ist. Hierzu nehmen wir an, dass rational ist. In diesem Fall existieren teilerfremde Zahlen und mit
Die Voraussetzung, dass Zähler und Nenner teilerfremd sind, ist gleichbedeutend damit, dass der Bruch bereits vollständig gekürzt vorliegt. Durch Quadrieren beider Seiten der Gleichung erhalten wir:
muss also das Doppelte von sein und ist somit eine gerade Zahl. Nun ist das Quadrat einer Zahl genau dann gerade, wenn die Zahl selbst gerade ist. Demnach muss auch gerade sein und es gibt damit ein mit . Setzen wir dies in die obige Gleichung ein, so folgt:
Kannst du erkennen, welches Problem nun auftritt? Da gerade ist, muss auch gerade sein. Somit kann man den Bruch durch kürzen. Dies widerspricht jedoch der Annahme, dass und teilerfremd sind. Wir hatten nämlich und so gewählt, dass vollständig gekürzt ist. Es folgt, dass keine rationale Zahl sein kann.
Frage: Warum ist das Quadrat einer Zahl genau dann gerade, wenn gerade ist?
Zunächst zeigen wir: Ist eine Zahl gerade, so ist auch ihr Quadrat gerade. Sei eine gerade Zahl. Dann gibt es eine natürliche Zahl mit . Es folgt
Damit ist das Quadrat von auch eine gerade Zahl. Nun zeigen wir die Rückrichtung (die wir für unseren Beweis benötigen): Ist das Quadrat einer Zahl gerade, so ist auch die Zahl selbst gerade. Dies beweisen wir mittels Kontraposition, indem wir zeigen: Ist eine Zahl ungerade, so ist auch ihr Quadrat ungerade. Sei also eine ungerade Zahl. Damit gibt es eine natürliche Zahl mit . Es folgt
Damit ist eine ungerade Zahl.
Baustelle: Beweis der Existenz einer Wurzel[Bearbeiten]
Wir haben uns gerade überlegt, dass in den rationalen Zahlen Wurzeln nicht immer existieren müssen. In hingegen werden wir sehen, dass dies schon der Fall ist. Die Struktur-Eigenschaft, die von unterscheidet, ist die Vollständigkeit der reellen Zahlen. Diese hatten wir über rationale bzw. allgemeine Intervallschachtelungen definiert. Um also die Existenz einer Wurzel in den reellen Zahlen beweisen zu können, müssen wir das Intervallschachtelungsprinzip verwenden.
In einem ersten Schritt beweisen wir, dass eine reelle Zahl ist bzw. dass es eine nicht-negative reelle Zahl mit gibt. Um das Intervallschachtelungsprinzip anwenden zu können, müssen wir eine Intervallschachtelung konstruieren, die als einziges Element enthält.
Da wir allerdings nicht wissen, wo genau auf dem Zahlenstrahl liegt, müssen wir einen Trick anwenden, der darin besteht, "simultan" zur Intervallschachtelung für eine Intervallschachtelung für zu konstruieren, denn ist die Zahl, für die gilt, und von wissen wir ja, wo sie genau auf dem Zahlenstrahl liegt. Bei diesem "simultanen" Verfahren müssen wir allerdigs sicherstellen, dass für alle gilt, denn dadurch stellen wir auch sicher, dass die gesuchte Zahl in allen Intervallen enthalten bzw. für alle ist.
Fangen wir also mit den Anfangsintervallen bzw. an und setzen dabei als untere Grenze , so dass ist. Als obere Grenze setzen wir , so dass ist. Damit sind und unsere ersten beiden Intervalle.
Nun wählen wir die Standardmethode für Intervallschachtelungen, indem wir für die nächsten beiden Intervalle unserer Schachtelung das Intervall "halbieren". Für müssen wir uns nun zwischen und entscheiden. Wir wissen bereits, dass Grundbedingung für ist. Also entscheiden wir uns für , denn tatsächlich ist . Damit sind und unsere neuen Intervalle.

Dieses Prinzip setzen wir nun beliebig fort. Für ergibt sich , denn und .
Ganz allgemein definieren wir unsere Intervallschachtelung folgendermassen:
Setze und für : , und
Dann ist tatsächlich eine Intervallschachtelung, denn zum Einen gilt (nach Konstruktion) für alle . Zum Anderen ist
Daher gibt es nach einer Folgerung zum archimedischen Axiom zu jedem ein mit . Damit gibt es genau eine reelle Zahl , die von der Intervallschachtelung approximiert wird.
Wir müssen nun aber noch zeigen, dass tatsächlich gilt. Dies folgt leider noch nicht automatisch, da wir in der Konstruktion der Intervallschachtelung die Bedingung und nicht benutzt hatten. Zunächst zeigen wir, dass ebenfalls eine Intervallschachtelung ist. Einerseits ist wieder nach Konstruktion für alle . Andererseits gilt
Da nun eine Intervallschachtelung war, existiert zu jedem aber auch ein mit . Damit gilt aber
Also ist ebenfalls eine Intervallschachtelung. Diese hat nun ebenfalls genau ein Element , das in allen Intervallen enthalten ist. Wir hatten aber nun so konstruiert, dass in allen Intervallen enthalten ist. Daraus folgt nun . Damit ist nun .
Also haben wir mit Hilfe einer Intervallschachtelung gezeigt, dass in existiert.
Ganz analog können wir nun folgenden Satz beweisen:
Satz (Existenz der Wurzel)
Ist und , so existiert die -te Wurzel von .
Zusammenfassung des Beweises (Existenz der Wurzel)
Wir verallgemeinern den Beweis von oben. Wir konstruieren dazu zwei Intervallschachtelungen und , so dass die Zahl und die -te Wurzel approximiert.
Beweis (Existenz der Wurzel)
Die Fälle und sind trivial. Es gilt für alle und für alle . Daher ist für alle und für alle .
Sei nun also und betrachten wir zunächst den Fall . Den anderen Fall werden wir später auf diesen zurückführen.
Wir konstruieren nun (analog zu oben) eine Intervallschachtelung wie folgt: , und für alle sei für
Dann gilt genau wie oben und für alle . Nach der Folgerung zum archimedischen Axiom gibt es zu jedem ein mit . Also ist eine Intervallschachtelung, die eine reelle Zahl approximiert.
Nun ist aber ebenfalls eine Intervallschachtelung, denn es gilt , sowie unter Verwendung der Formel
können wir folgern:
Da eine Intervallschachtelung ist, gibt es zu jedem ein mit . Dann gilt aber
Sei die reelle Zahl, die in allen Intervallen enthalten ist. Da wir aber so konstruiert hatten, dass gilt für alle , gilt . Dann gilt aber .
Betrachten wir noch den Fall : Es gilt . Mit dem eben gezeigten gibt es daher ein mit . Damit gilt dann aber . Also ist .
- @Benutzer:Stephan Kulla: Abschnitt muss noch überarbeitet werden.
- Es muss noch erklärt werden, was ist.
- Es sollten Abbildungen wie im Beweis zu Mathe für Nicht-Freaks: Satz von Bolzano-Weierstraß ergänzt werden.
Vertiefung: Wurzel im Komplexen[Bearbeiten]
In der Grundmenge der komplexen Zahlen besitzt die Potenzgleichung für genau Lösungen – auch wenn eine negative Zahl ist. Jede dieser Lösungen wird dann Wurzel der Potenzgleichung genannt. Während also im Reellen eine Zahl nur eine -te Wurzel besitzt, besitzt diese Zahl im Komplexen mehrere -te Wurzeln.







![{\displaystyle {\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7873203eb76042fcd24056c553de8c86054a2df)










![{\displaystyle {\sqrt[{2}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe5fde91c80468018bacc25e0b0e648840066517)




![{\displaystyle {\sqrt[{3}]{27}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f365d787e2e4b2b4a9015cf3af10ac91e12782d)
![{\displaystyle {\sqrt[{3}]{-27}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53c27a512b4ae50459b7d44652b58875fb370f0c)

![{\displaystyle {\sqrt[{3}]{27}}=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
![{\displaystyle {\sqrt[{n}]{.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a2023a9ba062fd6f13270208700eaaf8c5cc1a5)

![{\displaystyle f^{-1}={\sqrt[{n}]{.}}:\mathbb {R} _{0}^{+}\to \mathbb {R} _{0}^{+},\ x\mapsto {\sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b44f39e8dcca45ae4e8cf57ebcb8086e7f35a320)
![{\displaystyle {\sqrt[{n}]{.}}:\mathbb {R} _{0}^{+}\to \mathbb {R} _{0}^{+}:x\mapsto {\sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/742ac656d732ca5f2523a201ecacd45b4d1fe6e1)







![{\displaystyle a^{-{\tfrac {1}{n}}}={\tfrac {1}{\sqrt[{n}]{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca8f452771398b517b825929a19d8370cfa50520)
![{\displaystyle a^{\tfrac {1}{k}}={\sqrt[{k}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/769a163767e63955288e5beb6f0fdb8723ae97aa)












































![{\displaystyle I_{1}=[a_{1},b_{1}]=[1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08b0378633441ccc19580c1a2e581c8ab5779d0b)
![{\displaystyle I_{1}^{2}=[a_{1}^{2},b_{1}^{2}]=[1,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da0ac17f7b57b8e4a832f9bb4e0ec25c9f15d05a)
![{\displaystyle I_{1}=[1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3386ccdac4e0656a23439373319f470b6750a54a)

![{\displaystyle [1,{\tfrac {3}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb876caac560964ad3a96a2d7a8591455789b49a)
![{\displaystyle [{\tfrac {3}{2}},2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f6773c0ef8deb4ba59784d87beb33e9c54d4042)


![{\displaystyle I_{2}=[1,{\tfrac {3}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36f4025c069189737611a60e3d509bb97742443f)
![{\displaystyle 2\in [1^{2},\left({\tfrac {3}{2}}\right)^{2}]=[1,{\tfrac {9}{4}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c34110748346d20f1565e2fc7174e299088c3048)
![{\displaystyle I_{2}=[a_{2},b_{2}]=[1,{\tfrac {3}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be3a014323220634680f164a7067cbf95c0796ac)
![{\displaystyle I_{2}^{2}=[a_{2}^{2},b_{2}^{2}]=[1,{\tfrac {9}{4}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c7cc5479dd481b598d9e07d0ceba436231e04f5)

![{\displaystyle I_{3}=[{\tfrac {5}{4}},{\tfrac {3}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a5235cfb290d9ba412212f1028db0d7b213013)

![{\displaystyle 2\in [\left({\tfrac {5}{4}}\right)^{2},\left({\tfrac {3}{2}}\right)^{2}]=[{\tfrac {25}{16}},{\tfrac {9}{4}}]=I_{3}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92cdda68030e4c53a133df94dbf5f1b919bfbee1)


![{\displaystyle I_{n+1}={\begin{cases}\,[a_{n},m_{n}]&{\text{falls }}2\in [a_{n}^{2},m_{n}^{2}[,\\\,[m_{n},b_{n}]&{\text{falls }}2\in [m_{n}^{2},b_{n}^{2}].\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e4a7a048ac420341e8bdb0dbc2ac128309bb447)
















![{\displaystyle (I_{n})=([a_{n},b_{n}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6cf0e132a4323afb966154ee093462f6f1819c5)
![{\displaystyle (I_{n}^{k})=([a_{n}^{k},b_{n}^{k}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c2946d377834e7c12aeb6119a88e7522012048)






![{\displaystyle {\sqrt[{k}]{0}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ac1fb5b4ca13d21761b6ba994e50e1444493de8)
![{\displaystyle {\sqrt[{1}]{y}}=y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42648a24643eaf9f51038cbb370ce026c55b0081)



![{\displaystyle I_{1}=[a_{1},b_{1}]=[1,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35f7361e2f4f0f69b83c0a0d34ce35b5de79f18a)
![{\displaystyle I_{n+1}=[a_{n+1},b_{n+1}]={\begin{cases}\,[a_{n},m_{n}]&{\text{falls }}y=x^{k}\in [a_{n}^{k},m_{n}^{k}[,\\\,[m_{n},b_{n}]&{\text{falls }}y=x^{k}\in [m_{n}^{k},b_{n}^{k}].\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e18f044a4f7e30cfdef31f78246ae7004bdd0d87)








![{\displaystyle {\tilde {x}}=x={\sqrt[{k}]{y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a3b1ee3e33f72932be26ce7ee03acfe38b80bcd)




![{\displaystyle {\tfrac {1}{x}}={\sqrt[{k}]{y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37af3fe3760b148c57efa73c69b1553dc5060087)



