Buchanfang Maßtheorie by Richard4321/Die Volumenfunktion ist ein Prämaß auf dem Ring – Serlo „Mathe für Nicht-Freaks“

Motivation

In der Maßtheorie wollen wir Mengen ein Maß zuordnen. Bei Teilmengen aus $\mathbb {R}$ sind dies Längen, bei Teilmengen aus $\mathbb {R} ^{2}$ Flächen, bei Teilmengen aus $\mathbb {R} ^{3}$ Volumina und bei Teilmengen aus $\mathbb {R} ^{p}$ mit $p\geq 4$ verallgemeinerte Volumina. Dabei ordnen wir nur gewissen „guten“ Mengen ein Maß zu: das sind jene Mengen die wir durch Intervalle oder Rechtecke oder Quader "gut" überdecken können.

Wo stehen wir

Zuerst haben wir nur sehr primitive geometrische Figuren, wie Intervalle, Rechtecke oder (verallgemeinerte) Quader betrachtet und deren Eigenschaften zum Halbring verallgemeinert (mit $A,B\in H$ sind auch $\emptyset ,A\cap B\in H$ und $A\backslash B$ ist endliche disjunkte Vereinigung von Elementen aus $H$). Danach haben wir endliche disjunkte Vereinigungen von Halbringelementen eingeführt und zum Ring erklärt (mit $A,B\in R$ sind auch $\emptyset ,A\cup B,A\backslash B\in R$). Daraufhin haben wir unsere Flächenfunktion verallgemeinert zu einem additiven Inhalt bzw. sigma-additiven Prämaß, zuerst auf dem Halbring, dann auf dem Ring und deren Eigenschaften untersucht. Jetzt zeigen wir, dass unsere Flächen-/Volumenfunktion ein Prämaß ist. Damit lässt sie sich zu einem Maß fortsetzen: dem Lebesguemaß.

Zur Übersicht der Maßheorie-Herleitung geht es hier Mathe_für_Nicht-Freaks:_Buchanfang_Maßtheorie_by_Richard4321/_Allgemeine_Konstruktion_eines_Maßes

Die Volumenfunktion ist ein Prämaß

Satz (Die Volumenfunktion $l$ ist sigma-additiv auf $F^{p}$)

Auf dem Ring der endlich vielen disjunkten (verallgemeinerten) Quader $F^{p}$ ist das (verallgemeinerte) Volumen

$l:F^{p}\rightarrow [0,\infty ),\biguplus _{j=1}^{m}(a^{j},b^{j}]\mapsto \sum _{j=1}^{m}\prod _{i=1}^{p}(b_{i}^{j}-a_{i}^{j})$

sigma-additiv, also ein Prämaß.

Beweis (Die Volumenfunktion $l$ ist sigma-additiv auf $F^{p}$)

$l$ ist sigma-additiv auf $I^{p}$:

Wir haben schon gezeigt, dass $l$ endlich additiv und somit ein Inhalt ist auf dem Halbring $I^{p}$ und haben dann mit einem kleinen Fortsetzungssatz die endliche Additivität auf dem Ring $F^{p}$ erhalten. Wir zeigen nun die Sigma-Adidtivität auf $I^{p}$: Ein Rechteck oder ein (verallgemeinerter) Quader werde unterteilt in abzählbar viele disjunkte Rechtecken oder (verallgemeinerte) Quadern:

$\biguplus _{j=1}^{\infty }(a^{j},b^{j}]=(a,b]\in I^{p}$.

In unserer bildlichen Vorstellung ist das angedeutet durch

durch Überlappung verringert sich die Fläche

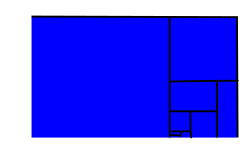
Die Beweisstrategie: Wir überdecken das kompakte $[a,b]$ mit den abzählbar vielen offenen (!) $(a^{j}-\delta _{j},b^{j}+\delta _{j})$ und erhalten wegen der Kompaktheit, dass endlich viele der $(a^{j}-\delta _{j},b^{j}+\delta _{j})$ zur Überdeckung genügen. Ohne Einschränkung sind das die ersten $n$ Stück, in Formeln

${\begin{aligned}\lbrack a,b\rbrack \subseteq \bigcup _{j=1}^{n}(a^{j}-\delta _{j},b^{j}+\delta _{j})\end{aligned}}$

Es folgt, dass auch $(a,b]$ von den ersten $n$ $(a^{j}-\delta _{j},b^{j}+\delta _{j}]$ überdeckt wird

${\begin{aligned}(a,b]\subseteq \bigcup _{j=1}^{n}(a^{j}-\delta _{j},b^{j}+\delta _{j}]\end{aligned}}$

Jetzt steht rechts eine endliche Vereinigung, d.h. wir können die Monotonie und die Subadditivität von $l$ auf dem Ring $F^{p}$ nutzen. Wir wählen die $\delta _{j}$ unterschiedlich und so klein, dass $l((a,b])$ bis auf ein festes, beliebig gewähltes $\epsilon$ in der Nähe von

${\begin{aligned}\sum _{j=1}^{\infty }l((a^{j}-\delta _{j},b^{j}+\delta _{j}])\end{aligned}}$

liegt. Dann haben wir die Sigma-Additivität bewiesen.

Der formale Beweis: Wegen

${\begin{aligned}l((a^{j},b^{j}])=\prod _{i=1}^{p}(b_{i}^{j}-a_{i}^{j})\end{aligned}}$

betrachten wir die in $x$ stetige Funktion

$x\mapsto \prod _{i=1}^{p}(x+b_{i}^{j}-a_{i}^{j})$

Sei $\epsilon >0$ beliebig. Wegen der Stetigkeit gibt es für alle $j$ ein $\delta _{j}>0$ sodass für $2x\leq \delta _{j}$ gilt

$\left|\prod _{i=1}^{p}(2x+b_{i}^{j}-a_{i}^{j})-\prod _{i=1}^{p}(b_{i}^{j}-a_{i}^{j})\right|<{\frac {\epsilon }{2^{j}}}$

d.h. wir können die Fläche/das (verallgemeinerte) Volumen der oben verwendeten $(a^{j}-\delta _{j},b^{j}+\delta _{j}]$ abschätzen als

${\begin{aligned}l((a^{j}-\delta _{j},b^{j}+\delta _{j}])=&\prod _{i=1}^{p}(2\delta _{j}-b_{i}^{j}-a_{i}^{j})\\<&\prod _{i=1}^{p}(b_{i}^{j}-a_{i}^{j})+{\frac {\epsilon }{2^{j}}}\\=&l((a^{j},b^{j}])+{\frac {\epsilon }{2^{j}}}\end{aligned}}$

Da $(a,b]$ sich nach Voraussetzung als abzählbare Vereinigung darstellen lässt

$(a,b]=\bigcup _{j=1}^{\infty }(a^{j},b^{j}]$

lässt sich $[a,b]$ überdecken mit offenen Mengen gemäß

$\left\lbrack a,b\right]\subseteq \bigcup _{j=1}^{\infty }(a^{j}-\delta _{j},b^{j}+\delta _{j})$

Da $[a,b]$ kompakt ist. wird $[a,b]$ schon von endlich vielen $(a^{j}-\delta _{j},b^{j}+\delta _{j})$ überdeckt.

Ohne Einschränkung von den ersten $n$. Das ergibt

$(a,b]\subseteq [a,b]\subseteq \bigcup _{j=1}^{n}(a^{j}-\delta _{j},b^{j}+\delta _{j})\subseteq \underbrace {\bigcup _{j=1}^{n}(a^{j}-\delta _{j},b^{j}+\delta _{j}]} _{\in F^{p}}$

Da $l$ ein Inhalt ist auf $F^{p}$, folgt mit dem letzten Kapitel mit der Monotonie und der Subadditivität (siehe Mathe_für_Nicht-Freaks:_Buchanfang_Maßtheorie_by_Richard4321/Eigenschaften_von_Inhalten_und_Prämaßen )

${\begin{array}{rcl}l((a,b])&{\stackrel {\text{Monotonie}}{\leq }}&l\left(\bigcup _{j=1}^{n}(a^{j}-\delta _{j},b^{j}+\delta _{j}]\right)\\&{\stackrel {\text{Subadditivität}}{\leq }}&\sum _{j=1}^{n}l(a^{j}-\delta _{j},b^{j}+\delta _{j}])\\&<&\sum _{j=1}^{n}\left(l((a^{j},b^{j}])+{\frac {\epsilon }{2^{j}}}\right)\\&\leq &\sum _{j=1}^{\infty }l((a^{j},b^{j}])+\sum _{j=1}^{n}{\frac {\epsilon }{2^{j}}}\\&<&\sum _{j=1}^{\infty }l((a^{j},b^{j}])+\epsilon \end{array}}$

Da $\epsilon >0$ beliebig ist, gilt

$l((a,b])\leq \sum _{j=1}^{\infty }l((a_{j},b_{j}])$

Die andere Ungleichung wurde im letzten Kapitel allgemein für Inhalte gezeigt:

$\sum _{i=1}^{\infty }l(a_{i},b_{i}]\leq l\left(\biguplus _{i=1}^{\infty }(a_{i},b_{i}]\right)=l((a,b])$

und es folgt

$\sum _{i=1}^{\infty }l((a_{i},b_{i}])=l\left(\biguplus _{i=1}^{\infty }(a_{i},b_{i}]\right)$

$l$ ist sigma-additiv auf $F^{p}$:

Wir haben schon in einem kleinen Fortsetzungssatz gezeigt, dass die Fortsetzung eines Prämaßes von einem Halbring auf einen Ring ein Prämaß ergibt, siehe Mathe_für_Nicht-Freaks:_Buchanfang_Maßtheorie_by_Richard4321/Inhalte_und_Prämaße_auf_(Halb-)Ringen