Das Mehrkörperproblem in der Astronomie/ Enge Begegnungen von Massenpunkten/ Glättung der Anziehungskraft

Idee

Der einfachste Weg, mit der tückischen $1/r^{2}$-Abhängigkeit fertig zu werden, besteht darin, das Newtonsche Gravitationsgesetz so zu glätten, dass auch für beliebig kleine Abstände zwischen zwei Massenpunkten eine endliche Kraft gegeben ist. Aarseth , ein bedeutender Pionier auf dem Gebiet der Mehrkörpersimulation, schlug 1963 vor, die gemäß Newton durch zwei Massen $m_{i}$ und $m_{j}$ repräsentierte potentielle Energie $E_{potN}=-Gm_{i}m_{j}/r$ durch einen Zusatzterm so abzuändern, dass sie auch gegenüber engen Begegnungen stabil bleibt:

$E_{potA}=-{\frac {Gm_{i}m_{j}}{\sqrt {r^{2}+\epsilon ^{2}}}}$

Man erkennt sofort, dass damit eine endliche Untergrenze $E_{potA,min}$ für die potentielle Energie festgelegt ist:

$E_{potA,min}=-{\frac {Gm_{i}m_{j}}{\epsilon }}$

Wie nachfolgend gezeigt wird, garantiert diese Begrenzung der potentiellen Energie zugleich auch eine Limitierung der Kraft auf einen endlichen Wert.

Physikalisch bedeutet die Glättung, dass man davon ausgeht, dass zwei Mitglieder eines Mehrkörpersystems sich effektiv nur bis auf einen Abstand $\epsilon$ nähern, d.h. enge Begegnungen zweier Körper für dieses keine Rolle spielen. Dieser effektive Mindestabstand wird Plummerradius genannt (benannt nach Plummer , welcher diesen bereits 1911 einführte, um die räumliche Verteilung der Sterne in einem Kugelhaufen zu beschreiben).

Modifikation des Gravitationsgesetzes durch Einführung einer Abhängigkeit des Typs $E_{pot}=-GMm/{\sqrt {r^{2}+\epsilon ^{2}}}$ für die durch zwei Punktmassen $M$ und $m$ repräsentierte potentielle Energie. $\epsilon$ definiert einen effektiven Mindestabstand zweier Massenpunkte für eine entsprechende Mehrkörpersimulation

Aarseths Glättungstechnik wird auch heutzutage verwendet, man siehe dazu z.B. den Aufsatz von Dehnen und Read (2011) , welcher einen Überblick über verschiedenen Verfahren der Mehrkörpersimulation gibt.

Auswirkungen der Modifikation

Abhängigkeit der potentiellen Energie von der Entfernung

Die Einführung eines in Wahrheit gar nicht existierenden Zusatzterms in das Gravitationsgesetz erscheint selbstverständlich sehr willkürlich. Wie nachfolgendes Diagramm zeigt, beseitigt die Modifikation die ansonsten bei sehr kleinen Abständen auftretenden Energie- (und damit auch Kraft-) -Spitzen sehr effizient, unterschätzt betragsmäßig aber schon bei einem Abstand $r>\epsilon$ die durch zwei Körper definierte potentielle Energie deutlich. Für einen relativen Fehler von weniger als 1% ist eine Distanz von zumindest etwa 7 Plummerradien erforderlich.

Modifizierte potentielle Energie des Typs $1/{\sqrt {r^{2}+\epsilon ^{2}}}$, dargestellt für den Fall $\epsilon$ = 1 zusammen mit der korrekten $1/r$-Abhängigkeit nach Newton

Für eine genaue Analyse des Fehlers empfiehlt es sich, Aarseths Formel in folgende Form zu bringen:

$E_{potA}={\frac {r}{\sqrt {r^{2}+\epsilon ^{2}}}}E_{potN}={\frac {1}{\sqrt {1+{\frac {\epsilon ^{2}}{r^{2}}}}}}E_{potN}$

Der Nenner hat die Form ${\sqrt {1+x}}$. Falls $x<<1$ (d.h. für Abstände, die sehr groß im Vergleich zum Plummerradius sind), darf man $1/{\sqrt {1+x}}$ näherungsweise durch $1-x/2$ ersetzen. Damit erhält man:

$E_{potA}\approx E_{potN}\left(1-{\frac {\epsilon ^{2}}{2r^{2}}}\right)$

Der durch die Glättung bewirkte relative Fehler der potentiellen Energie fällt zu großen Entfernungen hin umgekehrt quadratisch mit dem Abstand ab. Obige Beziehung erklärt auch die Anmerkung zur Fehlerschwelle von 1%.

Abhängigkeit der Anziehungskraft von der Entfernung

Aus der Abhängigkeit der potentiellen Energie von der Entfernung lässt sich durch Anwendung des Arbeitsprinzips die entsprechende Abhängigkeit der Kraft $F(r)$ rekonstruieren. Dazu betrachtet man, um welchen Betrag $\Delta E_{pot}$ sich die potentielle Energie ändert, wenn man an einer bestimmten Stelle $r$ ein kleines Wegstück $\Delta r$ zurücklegt. Nach dem Arbeitsprinzip $\Delta E_{pot}=F(r)\Delta r$ liegt dann dort eine Kraft $F(r)=\Delta E_{pot}/\Delta r$ vor. Eine exakte mathematische Betrachtung (man bildet die 1.Ableitung der potentiellen Energie) liefert (siehe auch untenstehendes Diagramm):

$F(r)_{A}=Gm_{i}m_{j}{\frac {r}{(r^{2}+\epsilon ^{2})^{3/2}}}$

Modifizierte Gravitation des Typs $r/(r^{2}+\epsilon ^{2})^{3/2}$, dargestellt für den Fall $\epsilon$ = 1 zusammen mit dem korrekten $1/r^{2}$-Gesetz nach Newton

Wie die potentielle Energie unterschätzt Aarseths Modifikation schon bei Abständen $r>\epsilon$ auch die Anziehungskraft deutlich. Ein relativer Fehler von unter 1% wird nun erst ab einer Entfernung von circa 12 Plummerradien erreicht. Besonders überraschend wirkt auf den ersten Blick, dass $F(r)_{A}$ bei einer Distanz von ungefähr einem Plummerradius ein Maximum erreicht und zu verschwindendem Abstand hin auf 0 abfällt. Betrachtet man aber den Verlauf der potentiellen Energie $E_{potA}$, so erkannt man, dass diese sich bei sehr geringer Entfernung kaum noch ändert, wenn man sich um eine kleine Strecke $\Delta r$ bewegt. Nach dem Arbeitsprinzip muss dann aber auch die einwirkende Kraft sehr gering sein.

Physikalisch bedeutet Aarseths Glättung, dass man bei einer entsprechenden Simulation zwei Körper endlicher Ausdehnung sich störungsfrei gegenseitig durchdringen lässt, wenn diese sich sehr nahe kommen. Befindet sich die eine Masse genau in der Mitte der anderen, so heben sich aufgrund der Radialsymmetrie die von den einzelnen Teilchen ausgeübten Kräfte gegenseitig auf.

Um den relativen Fehler von $F(r)_{A}$ für große Abstände abzuschätzen, drückt man wie für die potentielle Energie das Ergebnis Aarseths als Vielfaches des korrekten Wertes Newtons aus:

$F(r)_{A}={\frac {r^{3}}{(r^{2}+\epsilon ^{2})^{3/2}}}F(r)_{N}={\frac {1}{\left(1+{\frac {\epsilon ^{2}}{r^{2}}}\right)^{3/2}}}F(r)_{N}$

Der Nenner hat jetzt die Form $(1+x)^{3/2}$. Im Falle $x<<1$ darf er näherungsweise durch den Ausdruck $1-3x/2$ wiedergegeben werden, d.h. es gilt:

$F(r)_{A}\approx F(r)_{N}\left(1-{\frac {3\epsilon ^{2}}{2r^{2}}}\right)$

Der relative Fehler der Anziehungskraft folgt also wie derjenige der potentiellen Energie einer umgekehrt quadratischen Abhängigkeit von der Entfernung.

Umlaufgeschwindigkeit und Bahnform

Mit der Modifikation der Anziehungskraft verändern sich natürlich auch die Bahnen der Massenpunkte. Betrachtet man z.B. die Umlaufsgeschwindigkeit auf einer Kreisbahn, so findet man nach dem Gleichsetzen von Zentripetal- und Schwerkraft anstelle der korrekten Geschwindigkeit $v_{N}$ jetzt eine verringerte Geschwindigkeit $v_{A}$ gemäß

$v_{A}^{2}={\frac {GMr^{2}}{(r^{2}+\epsilon ^{2})^{3/2}}}={\frac {r^{3}}{(r^{2}+\epsilon ^{2})^{3/2}}}v_{N}^{2}={\frac {1}{\left(1+{\frac {\epsilon ^{2}}{r^{2}}}\right)^{3/2}}}v_{N}^{2}$

$v_{A}={\frac {1}{\left(1+{\frac {\epsilon ^{2}}{r^{2}}}\right)^{3/4}}}v_{N}$

Für $x<<1$ darf man Ausdrücke der Form $1/(1+x)^{3/4}$ durch $1-3x/4$ ersetzen. Daraus folgt, dass der relative Fehler der Umlaufsgeschwindigkeit für Bahnradien, die weit größer als der Plummeradius sind, gleichfalls umgekehrt quadratisch mit dem Abstand abfällt:

$v_{A}\approx v_{N}\left(1-{\frac {3\epsilon ^{2}}{4r^{2}}}\right)$

Die reduzierte Umlaufsgeschwindigkeit hat zur Folge, dass ein auf einer Kreisbahn sich bewegender Massenpunkt gegenüber der korrekten, auf dem ungeglätteten Gravitationsgesetz beruhenden Position immer mehr hinterher hinkt. Für elliptische Orbits lässt sich ein weiterer Effekt aufzeigen. Ihre Lage im Raum ist nicht mehr fest, stattdessen drehen sie sich langsam von Umlauf zu Umlauf. Anstatt auf einer geschlossenen Ellipse bewegt sich der Körper auf einer Rosettenbahn.

Einschub für Fortgeschrittene: Runge-Lenz-Vektor und Drehung der Ellipsenbahn

Mittels des sogenannten Runge-Lenz-Vektors lässt sich allgemein zeigen, dass eine Drehung der Bahn immer dann auftritt, wenn die zwischen zwei Massenpunkten $m$ und $M$ auftretende Anziehungskraft vom $1/r^{2}$-Gesetz abweicht. Er ist durch folgenden Ausdruck definiert, wobei ${\vec {p}}$ und ${\vec {L}}$ den Impuls und Drehimpuls des umlaufenden Körpers sowie ${\vec {e}}_{r}$ den radialen Einheitsvektor darstellen:

${\vec {A}}={\vec {p}}\times {\vec {L}}-Gm^{2}M{\vec {e}}_{r}$

${\vec {A}}$ ist parallel zur großen Halbachse der Ellipse ausgerichtet mit Blickrichtung vom Brennpunkt zum Perihel. Eine Konstanz dieses Vektors bedeutet somit, dass die Ellipse ortsfest ist. Sie lässt sich leicht überprüfen, indem man die zeitliche Ableitung von ${\vec {A}}$ betrachtet:

${\frac {d{\vec {A}}}{dt}}={\frac {d{\vec {p}}}{dt}}\times {\vec {L}}+{\vec {p}}\times {\frac {d{\vec {L}}}{dt}}-Gm^{2}M{\frac {d{\vec {e}}_{r}}{dt}}$

Der Impuls ist gegeben durch das Produkt aus Masse und Geschwindigkeit, seine zeitliche Ableitung damit durch das Produkt aus Masse und Beschleunigung. Nach dem Newtonschen Kraftgesetz gibt letzteres aber gerade die auf $m$ angreifende Kraft an, welche nach dem Gravitationsgesetz wiederum durch $-GmM/r^{2}{\vec {e}}_{r}$ beschrieben wird. Der zweite Term obiger Zeitableitung verschwindet, denn im Falle eines $1/r^{2}$-Kraftgesetzes ist der Drehimpuls konstant. Die Ableitung des Einheitsvektors im letzten Term ist durch die Winkelgeschwindigkeit ${\vec {\omega }}$ bestimmt, da ein solcher sich per Definition nur durch Drehung ändern kann. Aus all diesen Überlegungen folgt:

${\frac {d{\vec {A}}}{dt}}=-{\frac {GmM}{r^{2}}}{\vec {e}}_{r}\times {\vec {L}}-Gm^{2}M{\vec {\omega }}\times e_{r}$

Setzt man abschließend noch die Beziehung ${\vec {L}}=mr^{2}{\vec {\omega }}$ ein, so ergibt sich:

${\frac {d{\vec {A}}}{dt}}=0$

Für das Newtonsche Gravitationsgesetz verschwindet also die Zeitableitung von ${\vec {A}}$. Dieser Vektor ist damit tatsächlich konstant und so die Lage der Ellipse im Raum fest. Umgekehrt bedeutet das, dass eine Abweichung vom $1/r^{2}$-Gesetz die Konstanz des Runge-Lenz-Vektors und damit die Ortsfestigkeit der Ellipsenbahn aufhebt.

Die Planetenbahnen im Sonnensystem weisen in der Tat Drehungen ihrer Bahnen auf. Die Hauptursache hierfür ist, dass die auf einen Planeten wirkende Kraft nicht allein durch die Sonne, sondern in geringem Maße auch durch die übrigen Körper des Sonnensystems bestimmt ist. Durch diese gegenseitigen Störungen weichen die auf die Planeten angreifende Gesamtkräfte etwas vom $1/r^{2}$-Gesetz ab. Vor allem für die Merkurbahn tritt durch die von der Sonne hervorgerufenen Raumkrümmung eine zusätzliche Abweichung vom Newtonschen Gravitationsgesetz auf. Die auf gegenseitige Störungen beruhenden Drehungen der Planetenbahnen werden im Praxiskapitel weiter beleuchtet.

Die durch die Glättung des Gravitationsgesetzes hervorgerufenen Effekte seien schließlich anhand der Simulation eines Zwei-Körper-Systems veranschaulicht. $m_{i}$ ist dabei auf 1 Sonnenmasse, $m_{j}$ auf 1 Erdmasse gesetzt. Die Startpositionen sind (0/0) und (1 AE/0), die Anfangsgeschwindigkeiten (0/0) und (0/35 km/s). Die mit dynamischen Zeitschritten (was Gegenstand der nächsten Unterkapitel ist) durchgeführte Simulation überdeckt 10 Jahre.

Ohne Glättung ist die Ellipse wie erwartet ortsfest. Ein Plummerradius von 0.1 AE - 1/10 des Mindestabstandes der beiden Körper - zieht bereits eine signifikante Drehung der Bahn nach sich. Eine Simulation mittels des modifizierten Gravitationsgesetzes kann nur solche Strukturen korrekt wiedergeben, welche zumindest etwa 10 Mal größer als der Plummerradius sind. Mit einem $\epsilon$ von 0.5 AE (der Hälfte des Mindestabstands) tritt nicht nur eine extreme Drehung der Bahn mit jedem Umlauf auf, sie erstreckt sich aufgrund der weit unterschätzten Anziehungskraft bei festgehaltener Startgeschwindigkeit auch viel weiter. Strukturen einer Ausdehnung von wenigen Plummerradien können also keinesfalls auch nur annähernd korrekt durch eine entsprechende Simulation dargestellt werden.

Modifizierte Anziehungskraft des Typs $r/(r^{2}+\epsilon ^{2})^{3/2}$, demonstriert anhand der Simulation eines Zweikörpersystems mit dem Hermite-Polynome-Verfahren und dynamischen Zeitschritten über einen Zeitraum von 10 Jahren. $\epsilon$ ist auf 0 (blaue Kurve), 0.1 AE (rote Kurve) und 0.5 AE (grüne Kurve) gesetzt.

Trotz der enormen Verfälschung der Bahnen bei geringen Abständen zweier Massenpunkte ist die Glättung des Newtonschen Gravitationsgesetzes gerechtfertigt, da sie das unkontrollierte Auseinanderfliegen im Gefolge enger Vorübergänge dämpft. Ohne eine gesonderte Behandlung solcher Passagen neigen simulierte Mehrkörpersysteme dazu, sich in unrealistisch kurzer Zeit aufzulösen, was letztlich auch eine falsche Wiedergabe der großräumigen Dynamik bedeutet.

Vektorielle Darstellung von Beschleunigung und Ruck

Für eine Simulation unter Zuhilfenahme des Plummerradius wird ebenfalls die Vektordarstellung des (geglätteten) Gravitationsgesetzes benötigt. Die Beschleunigungen $a_{ij}$ und $a_{ji}$, welche zwei Massen $m_{j}$ und $m_{i}$ gegenseitig ausüben, lauten:

${{\vec {a}}_{ij}}={\frac {Gm_{j}}{(|{{\vec {r}}_{ji}}|^{2}+\epsilon ^{2})^{3/2}}}{\begin{pmatrix}x_{j}-x_{i}\\y_{j}-y_{i}\\z_{j}-z_{i}\end{pmatrix}}$

${{\vec {a}}_{ji}}=-{\frac {Gm_{i}}{(|{{\vec {r}}_{ji}}|^{2}+\epsilon ^{2})^{3/2}}}{\begin{pmatrix}x_{j}-x_{i}\\y_{j}-y_{i}\\z_{j}-z_{i}\end{pmatrix}}$

Für eine Lösung mittels der Hermite-Polynome müssen wiederum auch die wechselseitigen Rucks betrachtet werden, für welche sich folgende Beziehungen ergeben:

${{\vec {j}}_{ji}}=Gm_{j}\left({\frac {{\vec {v}}_{ji}}{(|{\vec {r}}_{ji}|^{2}+\epsilon ^{2})^{3/2}}}-3{\frac {({\vec {r}}_{ji}\cdot {\vec {v}}_{ji}){\vec {r}}_{ji}}{(|{\vec {r}}_{ji}|^{2}+\epsilon ^{2})^{5/2}}}\right)$

${{\vec {j}}_{ij}}=-Gm_{i}\left({\frac {{\vec {v}}_{ji}}{(|{\vec {r}}_{ji}|^{2}+\epsilon ^{2})^{3/2}}}-3{\frac {({\vec {r}}_{ji}\cdot {\vec {v}}_{ji}){\vec {r}}_{ji}}{(|{\vec {r}}_{ji}|^{2}+\epsilon ^{2})^{5/2}}}\right)$

Sowohl für Beschleunigung als auch Ruck genügt es, gegenüber den ursprünglichen Formeln in den Nennern jeweils $|{\vec {r}}_{ji}|^{2}$ durch $|{\vec {r}}_{ji}|^{2}+\epsilon ^{2}$ zu ersetzen.

Selbstverständlich können zwei Massenpunkte auch im Verlauf einer derartig modifizierten Simulation sich stärker als nur bis auf $\epsilon$ nähern. Der nach Newton dabei erfolgende starke Anstieg der Anziehungskraft wird jedoch dann ignoriert. Die beiden Körper laufen einander vorbei, ohne nach dem engsten Vorübergang mit abnorm hoher Geschwindigkeit wieder weit entfernt voneinander zu stehen.

Entfernungsabhängiger Plummerradius

Das soeben vorgestellte Beispiel eines Zwei-Körper-Systems zeigt einen wesentlichen Nachteil des ursprünglichen Glättungsverfahren Aarseths auf. Der dadurch eingeführte Fehler bei der Kraftberechnung erstreckt sich bis ins Unendliche, bei einem Abstand von 12 $\epsilon$ von einem Massenpunkt beträgt dieser immerhin noch 1% des Absolutwertes. Die Reichweite des Fehlers lässt sich aber begrenzen, indem man den Plummerradius mit einer entfernungsabhängigen Korrekturfunktion $u(r)$ multipliziert:

$F=Gm_{i}m_{j}{\frac {r}{(r^{2}+u^{2}(r)\epsilon ^{2})^{3/2}}}$

Um eine geeignete Funktion für $u(r)$ zu finden, werden an diese folgende Forderungen gestellt. Bei einer Entfernung von 2 $\epsilon$ soll die Korrektur gleich 0 sein, d.h. von da an weiter nach außen unverfälscht das Newtonsche Gravitationsgesetz gelten. Bei geringer werdender Distanz soll $u(r)$ kontinuierlich ansteigen und damit die Glättung entsprechend immer mehr verstärken, bis bei verschwindender Entfernung $u(r)$ den Wert 1 erreicht, d.h. die Modifikation voll wirksam wird. Mit diesem z.B. von Hernquist und Katz (1989) benutzten Ansatz bleiben die zwischen je zwei Massenpunkten betrachteten Kräfte für Entfernungen ab 2 $\epsilon$ fehlerfrei, d.h. die räumliche Auflösung einer Mehrkörpersimulation wird gegenüber der einfachen Methode deutlich verbessert.

Der Übergang vom korrekten $1/r^{2}$ - Gesetz zur Glättung $r/(r^{2}+\epsilon ^{2})^{3/2}$ soll möglichst sanft erfolgen. An der Stelle $2\epsilon$ soll die Kurve $r/(r^{2}+u^{2}(r)\epsilon ^{2})^{3/2}$ somit genau so steil verlaufen wie $1/r^{2}$, bei verschwindendem Abstand ebenso wie $r/(r^{2}+\epsilon ^{2})^{3/2}$. Eine vergleichsweise einfache Funktion, welche all die oben genannten Wünsche erüllt, lautet:

$u(r)=\left(1-{\frac {r^{2}}{4\epsilon ^{2}}}\right)^{n}$

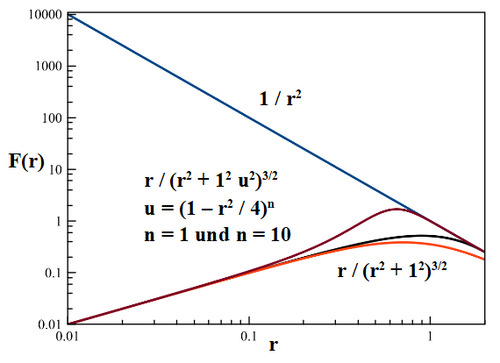
Der Exponent $n$ ist ein frei wählbarer Parameter. Die Korrekturfunktion ist nachfolgend für $n$ = 1 und $n$ = 10 dargestellt.

Kandidaten für eine Korrekturfunktion $u(r)$ für einen sanften Übergang zwischen dem korrekten Newtonschen Gravitationsgesetz $1/r^{2}$ und der Glättung $r/(r^{2}+\epsilon ^{2})^{3/2}$ nach Aarseth (1963)

Je höher man $n$ setzt, umso besser wird das Newtonsche Gravitationsgesetz auch für $r<2\epsilon$ angenähert. Um für einen gegebenen Plummerradius dadurch die Auflösung einer Mehrkörpersimulation signifikant zu steigern, sind aber sehr hohe Exponenten erforderlich. Wie untenstehende Abbildung zeigt, wird ein $n$ von 10 benötigt, um eine Auflösung von einem statt zwei Plummerradien zu erzielen. Die wiederholte Auswertung hoher Potenzen kann jedoch wiederum numerische Instabilitäten nach sich ziehen. Um detailliertere Strukturen zu modellieren, ist es daher geboten, stattdessen einen kleineren Plummerradius und die einfachste Einstellung $n$ = 1 zu verwenden. Damit ergibt sich folgendes Kraftgesetz:

$F(r)_{AN}=Gm_{i}m_{j}{\frac {r}{\left(r^{2}+\left(1-{\frac {r^{2}}{4\epsilon ^{2}}}\right)^{2}\epsilon ^{2}\right)^{3/2}}}=Gm_{i}m_{j}{\frac {64r\epsilon ^{3}}{(r^{2}+4\epsilon ^{2})^{3}}}$

Versuche eines sanften Übergangs zwischen dem korrekten Newtonschen Gravitationsgesetz $1/r^{2}$ und der Glättung $r/(r^{2}+\epsilon ^{2})^{3/2}$ nach Aarseth (1963), hier dargestellt für $\epsilon$ = 1. Die blaue Kurve zeigt die Kraftberechnung nach Newton, die rote die voll geglättete. Die schwarze bzw. braune Linie geben die Korrekturen auf Grundlage eines Exponenten von 1 bzw. 10 für $u(r)$ an

Dementsprechend üben zwei Massenpunkte bei Abständen von unter $2\epsilon$ folgende Beschleunigungen aufeinander aus:

${{\vec {a}}_{ij}}={\frac {64Gm_{j}\epsilon ^{3}}{(|{{\vec {r}}_{ji}}|^{2}+4\epsilon ^{2})^{3}}}{\begin{pmatrix}x_{j}-x_{i}\\y_{j}-y_{i}\\z_{j}-z_{i}\end{pmatrix}}$

${{\vec {a}}_{ji}}=-{\frac {64Gm_{i}\epsilon ^{3}}{(|{{\vec {r}}_{ji}}|^{2}+\epsilon ^{2})^{3}}}{\begin{pmatrix}x_{j}-x_{i}\\y_{j}-y_{i}\\z_{j}-z_{i}\end{pmatrix}}$

Die unter solchen Bedingungen wechselseitig ausgeübten Rucks sind:

${{\vec {j}}_{ji}}=64Gm_{j}\epsilon ^{3}\left({\frac {{\vec {v}}_{ji}}{(|{\vec {r}}_{ji}|^{2}+4\epsilon ^{2})^{3}}}-6{\frac {({\vec {r}}_{ji}\cdot {\vec {v}}_{ji}){\vec {r}}_{ji}}{(|{\vec {r}}_{ji}|^{2}+4\epsilon ^{2})^{4}}}\right)$

${{\vec {j}}_{ij}}=-64Gm_{i}\epsilon ^{3}\left({\frac {{\vec {v}}_{ji}}{(|{\vec {r}}_{ji}|^{2}+4\epsilon ^{2})^{3}}}-6{\frac {({\vec {r}}_{ji}\cdot {\vec {v}}_{ji}){\vec {r}}_{ji}}{(|{\vec {r}}_{ji}|^{2}+4\epsilon ^{2})^{4}}}\right)$

Die potentielle Energie zweier Massenpunkte bei kleinen Abständen lautet:

$E_{pot}=-Gm_{i}m_{j}\left({\frac {16\epsilon ^{3}}{(|{{\vec {r}}_{ji}}|^{2}+4\epsilon ^{2})^{2}}}+{\frac {1}{4\epsilon }}\right)$

Einschub für Fortgeschrittene: Verifizierung der Korrekturfunktion

Dass die Korrekturfunktion $u(r)=1-r^{2}/4\epsilon ^{2}$ die Anforderungen $u(0)$ = 1 und $u(2\epsilon )$ = 0 erfüllt, kann man durch Einsetzen schnell erkennen. Um zu sehen, dass das entsprechend modifizierte Gravitationsgesetz sich auch an die Beziehungen Aarseths und Newtons anschmiegt, muss man die 1. Ableitung nach $r$ für all diese Formeln betrachten. Diese lauten (wobei der Faktor $Gm_{i}m_{j}$ nun fortgelassen wird):

${\frac {dF_{N}}{dr}}=-{\frac {2}{r^{3}}}$

${\frac {dF_{A}}{dr}}={\frac {1}{(r^{2}+\epsilon ^{2})^{3/2}}}-{\frac {3r^{2}}{(r^{2}+\epsilon ^{2})^{5/2}}}$

${\frac {dF_{AN}}{dr}}={\frac {1}{(r^{2}+u^{2}(r)\epsilon ^{2})^{3/2}}}-{\frac {3r\left(r+u(r){\frac {du(r)}{dr}}\epsilon ^{2}\right)}{(r^{2}+u^{2}(r)\epsilon ^{2})^{5/2}}}$

An der Stelle $r$ = 0 verschwindet für $dF_{AN}/dr$ der ganze rechte Term. Zugleich ist im linken Term $u(r)$ = 1, so dass sich $dF_{AN}/dr=1/\epsilon ^{3}$ ergibt. Dies aber stimmt mit $(dF_{A}/dr)(0)$ überein.

Für $r=2\epsilon$ ist $u(r)$ = 0, so dass alle entsprechenden Glieder von $dF_{AN}/dr$ verschwinden. Es resultiert $dF_{AN}/dr=-2/r^{3}$ entsprechend dem Wert von $(dF_{N}/dr)(2\epsilon )$.

Festlegung des Plummerradius

Ob eine Simulation mit Aarseths Ansatz realitätsnah ist oder nicht, und welchen Wert dafür der Plummerradius aufweisen soll, hängt sehr stark von der Art des zu untersuchenden Systems ab. Generell gilt, dass die Glättung der Anziehungskraft umso stärker ausfällt, je größer $\epsilon$ gewählt wird. Große Plummerradien dürfen dann verwendet werden, wenn man nur an weiträumigen Bewegungsmustern interessiert ist und die Materie, welche diese dominiert, diffus verteilt ist. Dies trifft z.B. für die Rotation von (Balken)spiralgalaxien zu, welche nicht durch die Gravitation der sichtbaren Sterne, sondern durch diejenige der dunklen Materie beherrscht wird. Auch die Bewegungen der Sterne in elliptischen Galaxien sowie diejenige der Galaxien untereinander in Galaxienhaufen werden durch die diffus verteilte dunkle Materie dominiert.

In Sternhaufen spielt wegen ihrer im Vergleich zu Galaxien oder gar Galaxienhaufen sehr geringen Abmessungen die dunkle Materie keine Rolle, die Bewegungen der einzelnen Mitglieder werden vollständig durch deren eigene Anziehungskräfte dominiert. Dementsprechend müssen auch lokale Ereignisse berücksichtigt werden, so dass nur kleine Plummerradien zulässig sind oder unter Umständen gar nicht verwendet werden dürfen. Ein Beispiel für Letzteres ist der schon in der Einleitung erwähnte Haufen R136, wo einzelne Sterne sich so nahe kommen können, dass diese sogar miteinander kollidieren und so zu äußerst massereichen Sternen verschmelzen. Enge Vorübergänge müssen dann unbedingt mit dynamischer zeitlicher Schrittweite behandelt werden, worauf Aarseth zusammen mit Hoyle selbst 1964 hingewiesen hat.

Auch bei der Behandlung von Galaxienkollisionen muss eine gewisse Kleinräumigkeit in Betracht gezogen werden. Zwar muss wie für eine isolierte Galaxie nicht jeder Stern einzeln berücksichtigt werden, doch verändert sich der ursprüngliche Aufbau der Stoßpartner grundlegend.

Berücksichtigung lokaler Strukturen

White schlug anhand des Beispiels kollidierender Galaxien 1979 vor, für den Plummerradius den Radius derjenigen Kreisbahn zu verwenden, auf der ein Massenpunkt mit einer charakteristischen Masse $m$ mit einer für das Sternsystem typischen Geschwindigkeit $v$ umkreist würde. Aus der entsprechenden Kreisbahngeschwindigkeit $v^{2}=Gm/\epsilon$ folgt

$\epsilon ={\frac {Gm}{v^{2}}}$

Die für das Mitglied eines Sternsystems typische Geschwindigkeit kann aus dessen Radius $R$ und Gesamtmasse $M$ abgeschätzt werden. Ein brauchbares Maß ist die Kreisbahngeschwindigkeit $V^{2}=GM/R$ eines Körpers, der das ganze Ensemble an dessen Rand umläuft. Drückt man noch $M$ durch die Anzahl $N$ der Mitglieder des Systems aus gemäß $M=Nm$, so erhält man:

$\epsilon ={\frac {R}{N}}$

Der Plummerradius folgt aus dem Radius des Systems geteilt durch die Anzahl dessen Massenpunkte. Die ebenfalls schon zu Beginn dieses Buches genannten Plejaden weisen einen Radius von etwa 2.5 Parsec auf und umfassen ungefähr 2100 Mitglieder. Damit ergibt sich $\epsilon$ = 2.5 Parsec / 2100 $\approx$ 0.0012 Parsec $\approx$ 250 astronomische Einheiten, was etwa dem 6-fachen der Entfernung des Pluto von der Sonne entspricht. Für den Kugelhaufen 47 Tucanae ist mit einem Radius von circa 18 Parsec und etwa 1 Million Sternen ein sehr viel kleinerer Plummerradius von nur 18 Parsec / 1000000 $\approx$ 0.000018 Parsec bzw. knapp 4 astronomischen Einheiten erforderlich - weniger als der Abstand des Jupiter von unserem Zentralgestirn.

Der typische relative Fehler der Anziehungskraft $\Delta F/F\sim \epsilon ^{2}/r^{2}$ - es wird die einfache Glättung $r/(r^{2}+\epsilon ^{2})^{3/2}$ betrachtet - weist folgende Charakteristik auf. Teilt man das Volumen eines Sternsystems durch die Anzahl seiner Mitglieder, so gewinnt man den mittleren Abstand $d\sim R/N^{1/3}$ zwischen zwei Körpern. Setzt man diesen zusammen mit dem Plummerradius in den relativen Fehler ein, so folgt:

${\frac {\Delta F}{F}}\sim {\frac {1}{N^{4/3}}}$

Die Simulation wird umso genauer, je mehr Massenpunkte betrachtet werden, wobei die Genauigkeit überproportional mit $N$ wächst. Für die Plejaden ergibt sich mit 2100 Mitgliedern ein relativer Fehler von einer Größenordnung zwischen 10^-5 und 10^-4, für 47 Tucanae mit 1 Million Sternen dagegen von nur 10^-8. Mit einem Plummerradius $R/N$ ist der durch Aarseths Verfahren eingeführte Fehler bei der Kraftberechnung also zumeist unkritisch.

Behandlung von Großstrukturen

Für die Behandlung ausgedehnter Strukturen im Kosmos verwendeten Power und andere 2003 den Ansatz, dass die maximale von einem Körper der Masse $m$ ausgeübte Beschleunigung $Gm/\epsilon ^{2}$ nicht größer sein soll als diejenige $GM/R^{2}$, welche ein Körper durch das ganze System an dessen Rand erfährt. Daraus folgt (wobei wiederum $M=Nm$ verwendet wird):

$\epsilon ={\frac {R}{\sqrt {N}}}$

Um den Plummerradius zu erhalten, genügt es nun, den Radius des Systems durch die Wurzel der Anzahl seiner Mitglieder zu teilen. Will man z.B. eine Galaxie mit einem Radius von 20000 Parsec mit 1 Million Massenpunkten modellieren, so benötigt man einen Plummerradius von 20000 Parsec / ${\sqrt {1000000}}$ = 20000 Parsec / 1000 = 20 Parsec.

Setzt man erneut Plummerradius und mittleren Abstand zweier Massenpunkte in $\Delta F/F$ ein, so findet man (abermals für Aarseths einfache Glättung):

${\frac {\Delta F}{F}}\sim {\frac {1}{N^{1/3}}}$

Mit Power's Methode ist demgemäß nur eine langsame Steigerung der Genauigkeit einer Simulation mit einer höheren Anzahl von Massenpunkten zu erwarten. Selbst mit 1 Million Körpern liegt noch ein relativer Fehler der Größenordnung 10^-2 vor. Mit einem Plummeradius $R/{\sqrt {N}}$ zieht die Glättung $r/(r^{2}+\epsilon ^{2})^{3/2}$ einen erheblichen Fehler für die Anziehungskraft nach sich, so dass eine räumliche Begrenzung der Glättung auf Abstände von höchstens 2 Plummerradien trotz des damit verbundenen höheren Rechenaufwands angebracht ist.

Der Ansatz $\epsilon =R/{\sqrt {N}}$ hat jedoch auch einen bedeutsamen Vorteil. Die maximale Beschleunigung, die ein Massenpunkt erleiden kann, ist aufgrund der Definition des Verfahrens auf $GM/R^{2}$ beschränkt, d.h. von seiner eigenen Masse $m$ unabhängig. Für die Stabilität der Simulation einer Galaxie oder gar eines Galaxienhaufens, wo $m$ üblicherweise in einer Größenordnung von Millionen Sonnenmassen liegt (weil eine Darstellung solcher Systeme auf der Ebene der Einzelsterne schlicht unmöglich ist) ist dies von fundamentaler Bedeutung.

Die hier vorgestellten Kriterien für die Festlegung des Plummerradius sind wie die Glättungsverfahren selbst aktuell geblieben (siehe dazu z.B. wiederum Dehnen und Read (2011) ).

C-Code: Beschleunigung, Ruck und Gesamtenergie im modifizierten Mehrkörpersystem

Die im Grundlagenkapitel vorgestellten Algorithmen und Prozeduren können hinsichtlich ihrer Struktur übernommen werden, doch muss jetzt unterschieden werden, ob der Abstand zweier Körper größer als das zweifache des Plummerradius ist oder nicht. Für letzteren Fall müssen die Interpolationsformeln zwischen dem exakten Gravitationsgesetz nach Newton und der Glättung gemäß Aarseth eingesetzt werden.

Alle bisherigen Variablen können übernommen werden. Für die Auswertung der Interpolationsformeln werden aber jetzt weitere, durch den Plummerradius modifizierte Potenzen des Abstands zweier Massepunkte gebraucht, wozu die Doubke d2, d4, d6 und d8 dienen. Der Plummerradius selbst wird durch die Double epsilon gekennzeichnet, welche den Prozeduren ebenfalls übergeben wird. Die Aufrufe lauten nun beschleunigung (objekt,N,epsilon,m,r,a[objekt]), ruck(objekt,N,epsilon,m,r,v,a[objekt],j[objekt]) und energie (N,epsilon,m,r,v,&Ekin,&Epot). Die in den Formeln immer wiederkehrenden 2. und 3. Potenzen des Plummerradius werden durch die Double epsilon2 und epsilon3 dargestellt.

/* Globale Variablen */

unsigned int objekt;
unsigned int N;
double epsilon, epsilon2, epsilon3;
double *m;
double **r;
double **v;
double **a;
double **j;
double Ekin,Epot;

void beschleunigung (unsigned int objekt, unsigned int N, double epsilon, double *m, double **r, double *a)
{
 
/* Lokale Variablen */
 
  unsigned int i,k;
  double dr[3];
  double d,d2,d3,d6;
 
  for (k = 0;k < 3;k ++)
  a[k] = 0;
 
  for (i = 0;i < N;i ++)
  {
    if (i != objekt)
    {

/* Abstandsvektor dr zwischen Körper i und objekt */

      for (k = 0;k < 3;k ++)
      dr[k] = r[i][k] - r[objekt][k];

/* Benötigte Potenzen des Abstandsbetrags für folgende Fälle                                    */
/* Abstand zwischen i und objekt > 2 Plummerradien -> exakt nach Newton                         */
/* Sonst                                           -> Interpolation zwischen Newton und Aarseth */

      d = betrag (dr);
      if (d > 2 * epsilon)
      d3 = pow (d,3);
      else
      {
        d2 = pow (d,2) + 4 * epsilon2;
        d6 = pow (d2,3);
      }

/* Beschleunigungen für folgende Fälle                                                          */
/* Abstand zwischen i und objekt > 2 Plummerradien -> exakt nach Newton                         */
/* Sonst                                           -> Interpolation zwischen Newton und Aarseth */
 
      for (k = 0;k < 3;k ++)
      {
        if (d > 2 * epsilon)
        a[k] += G * m[i] * dr[k] / d3;
        else
        a[k] += G * m[i] * 64 * epsilon3 * dr[k] / d6;
      }
    }
  }
}

void ruck (unsigned int objekt, unsigned int N, double epsilon, double *m, double **r, double **v,
           double *a, double *j)
{
 
/* Lokale Variablen */
 
  unsigned int i,k;
  double dr[3];
  double d,d2,d3,d5,d6,d8;
  double dv[3];
  double skalar;

  for (k = 0;k < 3;k ++)
  {
    a[k] = 0;
    j[k] = 0;
  }

  for (i = 0;i < N;i ++)
  {
    if (i != objekt)
    {

/* Abstandsvektor dr und vektorielle Geschwindigkeitsdifferenz dv zwischen Körper i und objekt */
/* Skalerprodukt von dr und dv                                                                 */

      for (k = 0;k < 3;k ++)
      {
        dr[k] = r[i][k] - r[objekt][k];
        dv[k] = v[i][k] - v[objekt][k];
      }
      skalar = skalarprodukt (dr,dv); 

/* Benötigte Potenzen des Abstandsbetrags für folgende Fälle                                    */
/* Abstand zwischen i und objekt > 2 Plummerradien -> exakt nach Newton                         */
/* Sonst                                           -> Interpolation zwischen Newton und Aarseth */

      d = betrag (dr);
      if (d > 2 * epsilon)
      {
        d3 = pow (d,3);
        d5 = pow (d,5);
      }
      else
      {
        d2 = pow (d,2) + 4 * epsilon2;
        d6 = pow (d2,3);
        d8 = pow (d2,4);
      }
 
/* Beschleunigungen und Rucks für folgende Fälle                                                */
/* Abstand zwischen i und objekt > 2 Plummerradien -> exakt nach Newton                         */
/* Sonst                                           -> Interpolation zwischen Newton und Aarseth */

      for (k = 0;k < 3;k ++)
      {
        if (d > 2 * epsilon)
        {
          a[k] += G * m[i] * dr[k] / d3;
          j[k] += G * m[i] * (dv[k] / d3 - 3 * skalar * dr[k] / d5);
        }
        else
        {
          a[k] += G * m[i] * 64 * epsilon3 * dr[k] / d6;
          j[k] += G * m[i] * 64 * epsilon3 * (dv[k] / d6 - 6 * dr[k] * skalar / d8);
        }
      }
    }
  }
}

void energie (unsigned int N, double epsilon, double *m, double **r, double **v, double *Ekin, double *Epot)
{
 
/* Lokale Variablen */
 
  unsigned int i,j,k;
  double dr[3];
  double d,d2,d4;
 
/* Berechnung der kinetischen Energie */
 
  *Ekin = 0;
  for (i = 0;i < N;i ++)
  *Ekin += m[i] * pow (betrag (v[i]),2) / 2;
 
/* Berechnung der potentiellen Energie */
 
  *Epot = 0;
  for (i = 0;i < N;i ++)
  {
    for (j = i + 1;j < N;j ++)
    {
      for (k = 0;k < 3;k ++)
      dr[k] = r[j][k] - r[i][k];
      d = betrag (dr);
 
/* Potentielle Energie für folgende Fälle                                                       */
/* Abstand zwischen i und objekt > 2 Plummerradien -> exakt nach Newton                         */
/* Sonst                                           -> Interpolation zwischen Newton und Aarseth */

      if (d > 2 * epsilon)
      *Epot -= G * m[i] * m[j] / d;
      else
      {
        d2 = pow (d,2) + 4 * epsilon2;
        d4 = pow (d2,2);
        *Epot -= G * m[i] * m[j] * (16 * epsilon3 / d4 + 1 / (4 * epsilon));
      }
    }
  }
}