Das Mehrkörperproblem in der Astronomie/ Praktische Beispiele/ Sternhaufen
Im Gegensatz zu einem Planetensystem besitzt ein Sternhaufen keine dominierende Zentralmasse. Selbst das massereichste Mitglied eines solchen kann bestenfalls einige Prozent der Gesamtmasse des Ensembles aufbieten. Wie schon das mehrfach in diesem Buch gezeigte, aus drei Sternen gleicher Masse bestehende System andeutet, kann man unter solchen Bedingungen nicht erwarten, dass sich auch nur halbwegs stabile, periodische Bahnen herausbilden. Das Verhalten eines Haufens durch die Positionen und Geschwindigkeiten der Einzelobjekte oder dazu äquivalente Parameter in Form von Bahnelementen zu beschreiben, macht daher keinen Sinn. Stattdessen ist es angebracht, zu einer statistischen Betrachtungsweise überzugehen und sich auf globale Eigenschaften des Haufens zu konzentrieren. Angesichts der oft völlig regellos erscheinenden Orbits seiner Mitglieder erweist sich dabei der Vergleich mit einem Gas, dessen Moleküle sich ebenfalls ungeordnet bewegen, als nützlich.
Vergleich mit einem Gas
[Bearbeiten]Virialsatz
[Bearbeiten]Wie schon im Grundlagenkapitel besprochen, ist in einem abgeschlossenen System die Gesamtenergie konstant, wobei diese bei Anwesenheit der Gravitation als einzige Kraft durch die Summe von kinetischer und potentieller Energie gegeben ist. Wie Rudolf Clausius 1870 erkannte, lässt sich für ein Gas in thermischem Gleichgewicht eine weitere nützliche Beziehung für das zeitliche Mittel diesen beiden Energieformen aufzeigen. Auf einen Sternhaufen übertragen, muss man als Analogie zum thermischen Gleichgewicht verlangen, dass die zeitlichen Mittel der Positionen und Geschwindigkeiten der einzelnen Sterne beschränkt bleiben. Unter dieser Voraussetzung gilt für ein wiederum ausschließlich der Schwerkraft unterliegendes System:
Die Richtigkeit dieses Satzes kann man anhand des ebenfalls bereits oft behandelten Spezialfalls einer Kreisbahn plausibel machen, auf welcher eine kleine Masse eine sehr viel größere Zentralmasse in einer Entfernung umkreist. In diesem Fall sind beide Energien konstant und die kinetische Energie (fast) allein durch die kleine Masse gegeben, da die große Masse (nahezu) unbeweglich in der Mitte ruht. Setzt man kinetische und potentielle Energie in obige Beziehung ein, so erhält man:
Durch Division mit r und Umstellen der Gleichung folgt daraus:
Dies aber ist genau die für eine Kreisbahn erforderliche Gleichheit von Zentripetal- und Anziehungskraft.
Betrachtet man eine beliebige Keplerbahn für , so wird die Notwendigkeit einer Mittelung der Energien deutlich. Aus der schon zur Bestimmung der Bahnelemente der Planeten herangezogenen Vis-Viva-Gleichung folgt, dass die Geschwindigkeit der umlaufenden Masse im Abstand von der Zentralmasse folgenden Wert aufweist:
Für eine Ellipse ist hierbei die große Halbachse positiv, für eine Hyperbel negativ, für eine Parabel unendlich (so dass für letztere der Term verschwindet). Hyberbel- und Parabelbahnen kommen für eine Diskussion des Virialsatzes jedoch nicht in Frage, da sich solche bis ins Unendliche erstrecken, d.h. die Anforderung der Beschränktheit für die Position nicht erfüllen. Die Energiebilanz für einen elliptischen Orbit lautet:
Der kleinstmögliche Abstand zwischen und ist durch gegeben, wobei wiederum die Exzentrizität der Bahn darstellt. Die maximale Distanz beträgt . Diese Grenzen für den Abstand zwischen und liefern folgendes Intervall für :
Kommen sich zwei Objekte in einem Mehrkörpersystem im Vergleich zu den Entfernungen der übrigen Körper sehr nahe, so bewegen sie sich während dieser Passage auf einer nur noch geringfügig gestörten Keplerbahn. Häufig handelt es sich dabei um einen Orbit, deren Exzentrizität nahe bei 1 liegt. Aus obiger Betrachtung folgt, dass aber gerade dann kurzzeitig einen sehr hohen Wert annehmen kann. Nach unten ist dagegen beschränkt. Macht man von einem Sternhaufen wiederholt Momentaufnahmen von , muss man starke Fluktuationen erwarten, die zwar nur relativ schwach ausgeprägte Minima, aber sehr prägnante Maxima aufweisen.
Relaxation
[Bearbeiten]Wie gerade diskutiert, setzt der Virialsatz voraus, dass das Ensemble sich in einem gewissen Gleichgewichtszustand befindet. Ein solcher wird erreicht, indem die Mitglieder des Systems untereinander Energie austauschen, wenn sie miteinander in Wechselwirkung treten. Ein Gasmolekül stößt ständig mit anderen Molekülen zusammen, ein Stern in einem Haufen erleidet immer wieder mehr oder weniger enge Vorübergänge anderer Sterne. Jedes derartige Ereignis ist mit einem Energieaustausch und einer Änderung der Bahn der Stoßpartner verbunden. Ein statistisches Gleichgewicht im System ist dann erreicht, wenn die Einzelobjekte im Mittel eine Energieänderung erfahren haben, welche so groß ist wie deren kinetische Energie selbst.
Dieser Übergang in den Gleichgewichtszustand durch permanenten Energieaustausch innerhalb des Ensembles wird Relaxation genannt, die dazu erforderliche Zeit Relaxationszeit . Im Falle eines Sternhaufens hängt diese von der Mitgliederzahl , seinem Radius und der Gesamtmasse ab. Die Diskussion von Röser und Tscharnuter (2012) [1] führt zu folgender Beziehung:
Je mehr Sterne sich in einem Haufen befinden und um so größer er ist, um so länger braucht er, bis er sich im Gleichgewicht befindet. Umgekehrt erreicht er ein solches um so schneller, je massereicher er ist. Drückt man den Haufenradius in Parsec und seine Masse in Sonnenmassen aus, so ergibt sich ein wesentlich handlicherer Ausdruck mit der Relaxationszeit in Jahren:
Für die Plejaden ergibt sich mit 2100 Mitgliedern, einem Radius von 2.5 Parsec und 690 Sonnenmassen eine Relaxationszeit von circa 56 Millionen Jahren. 47 Tucanae weist mit etwa 1 Million Sternen, einem Radius von 18 Parsec und circa 900000 Sonnenmassen ein von ungefähr 7.6 Milliarden Jahren auf, d.h. zwei Größenordnungen über der entsprechenden Zeitskala für die Plejaden. Der Kugelhaufen besitzt weit mehr Mitglieder und ist wesentlich ausgedehnter, was selbst durch die sehr viel größere Masse kaum kompensiert wird. Zwar sorgt die höhere Dichte vor allem im Zentrum für häufige enge Passagen zwischen den Sternen, doch aufgrund der vielen Mitglieder geht für den Haufen insgesamt der Energieaustausch nur langsam vonstatten.
Wie später noch diskutiert wird, können Sterne durch enge Vorübergänge untereinander so stark beschleunigt werden, dass sie tatsächlich das Gesamtsystem verlassen. Streng genommen ist so der Virialsatz nicht wirklich gültig und ein Gleichgewicht in dessen Sinne für einen Sternhaufen gar nicht erreichbar. Man kann allerdings beobachten, das die zeitlichen Mittel von kinetischer und potentieller Energie das Theorem dennoch in sehr guter Näherung befolgen.
Zum Schluss dieses Abschnitts soll die Relaxationszeit mit der dynamischen Zeit verglichen werden. Das Verhältnis der beiden Zeiten ist proportional der Anzahl an Zeitschritten, welche für eine Simulation der Dauer abgearbeitet werden müssen. Im Kapitel "Enge Begegnungen von Massenpunkten" wurde im Unterkapitel "Dynamische Zeitskalen" bereits gezeigt, dass . Drückt man die typische Sternmasse durch aus, so erhält man . Andererseits gilt wie soeben gezeigt . Einsetzen liefert:
Die erforderliche Anzahl an Zeitschritten für die Simulation eines Sternhaufens hängt also allein von der Anzahl dessen Mitglieder, nicht aber seiner Größe oder Masse ab. Die Abhängigkeit von ist leider sehr stark, für einen Haufen mit der 10-fachen Anzahl an Sternen muss bereits etwa das 50-fache an Zeitschritten aufgewandt werden.
Anfangsbedingungen
[Bearbeiten]Im Falle eines Planetensystems hat man es mit nur wenigen Körpern zu tun, so dass man deren anfängliche Positionen und Geschwindigkeiten per Hand festlegen kann. Zudem lassen sich diese Größen für die Planeten des Sonnensystems mit hoher Genauigkeit bestimmen. Bei einem aus tausenden oder gar Millionen Sternen bestehenden Haufen kommt ein solches Vorgehen nicht in Frage. Zwar kann man die Positionen der Mitglieder eines Haufens am Himmel genau angeben (sofern dieser sich noch in Einzelobjekte auflösen lässt), nicht aber deren Abstände untereinander in Blickrichtung. Bei den Geschwindigkeiten verhält es sich genau umgekehrt. Der Dopplereffekt liefert präzise die Geschwindigkeitskomponente in Blickrichtung. Die Komponente senkrecht dazu ist jedoch, wenn überhaupt, mit viel geringerer Genauigkeit bekannt. Sie folgt aus winzigen Änderungen der Positionen der Gestirne über einen genügend langen Zeitraum. Je weiter das System entfernt ist, umso geringer fallen diese Verschiebungen aus und sind dementsprechend schließlich nicht mehr nachweisbar.
Anstatt jedem einzelnen Stern gemessene Anfangsbedingungen zuzuweisen, arbeitet man schon zu Beginn der Simulation eines Haufens mit globalen Eigenschaften. Die wichtigsten davon sind die Häufigkeit, mit der bestimmte Sternmassen und Geschwindigkeiten auftreten, sowie die Sterndichte in Abhängigkeit vom Abstand zum Zentrum des Systems. Für solche statistischen Eigenschaften lassen sich Anfangsdaten weit zuverlässiger angeben als für jedes einzelne Objekt. Der Übergang zu individuellen Anfangsbedingungen geschieht, indem man jedem Stern eine zufällige Masse, Position und Geschwindigkeit zuordnet. Die Wahrscheinlichkeiten, mit denen Zufallszahlen bestimmte Werte annehmen, werden dabei an die beobachteten statistischen Gesetzmäßigkeiten angepasst.
Sternmassen
[Bearbeiten]Schon seit langem ist bekannt, dass massereiche Sterne viel seltener sind als massearme. Salpeter (1955) [2] bestimmte erstmalig mit relativ hoher Genauigkeit die Häufigkeit , mit welcher Sternmassen in der Umgebung der Sonne auftreten. Er fand, dass sich für Einzelsterne gut durch ein Potenzgesetz beschreiben lässt:
Neuere Untersuchungen haben gezeigt, dass für sehr massearme Sterne unterhalb von 0.5 Sonnenmassen, den sogenannten Roten Zwergen, nicht mehr so steil von abhängt. Dank sehr empfindlicher Instrumente sind in den letzten Jahrzehnten auch die sogenannten Braunen Zwerge der Beobachtung zugänglich geworden. Für diese zeigt die Häufigkeitsverteilung einen noch flacheren Verlauf. Kroupa (2001) [3] gibt für Körper zwischen 0.01 und 50 Sonnenmassen folgende Beziehungen an:
Die Wahrscheinlichkeit, ein Objekt zwischen 0.01 und 50 Sonnenmassen zu finden, muss natürlich gleich 1 sein. Daraus ergibt sich für den Faktor ein Wert von 1.987601. Die entsprechende Kurve ist nachfolgenden dargestellt.

Aus den Angaben Kroupas folgt, dass braune Zwerge etwa 37.2% der für einen Sternhaufen relevanten Körper stellen. Rote Zwerge weisen einen Anteil von ungefähr 47.8%, die übrigen Sterne einen solchen von etwa 15.0% auf. Objekte mit weniger als 0.01 Sonnenmassen sind, wie die vielen kleinen Körper im Sonnensystem zeigen, natürlich am zahlreichsten. Jedoch ist deren Gesamtmasse so gering, dass sie für die Dynamik eines Haufens keine Rolle spielen. Umgekehrt existieren auch Sterne mit mehr als 50 Sonnenmassen. Solche sind aber äußerst kurzlebig, so dass sie nur in sehr jungen, wenige Millionen Jahre alten Sternhaufen anzutreffen sind.
Aus der viel größeren Häufigkeit massearmer Sterne folgt, dass eine Zufallszahl zwischen 0 und 1 viel öfter einer geringen Masse zugeordnet werden muss als einer hohen. Um dies zu erreichen, geht man folgendermaßen vor. Man betrachtet die Wahrscheinlichkeit , einen Stern mit einer Masse von höchsten Sonnenmassen herauszugreifen. Diese ist durch die Fläche zwischen 0.01 und M unter obiger Kurve gegeben. Die Integralrechnung liefert:
Durch Umstellen der Formeln und Ausrechnen der Konstanten gewinnt man die zu einer Zufallszahl gehörige Masse :
Dichteverteilung
[Bearbeiten]Ein Sternhaufen darf oft als kugelsymmetrisch betrachtet werden, so dass dann dessen Dichte nur vom Abstand von Zentrum abhängt, nicht aber auch von anderen Größen. Der Verlauf der Dichte mit zunehmender Entfernung vom Mittelpunkt kann aus Sternzählungen abgeschätzt werden (sofern auch die Zentralregion des Ensembles in Einzelobjekte aufgelöst werden kann), was jedoch nur für sehr junge Sternhaufen ein Abbild des Anfangszustands liefert. Insbesondere die Kugelhaufen im galaktischen Halo sind schon sehr alt, so dass man davon ausgehen muss, dass sich deren Dichteverteilung seit ihrer Entstehung stark verändert hat. Um auch in solchen Fällen zu einer Aussage über den ursprünglichen Zustand zu gelangen, muss man von der Bildung des Systems aus einer kollabierenden Gaswolke ausgehen und abschätzen, welche Gesetzmäßigkeit sich während der Kontraktion bis zur Sternentstehung einstellt. Beide Verfahren zeigen, dass schon nach Abschluss dieser ersten Entwicklungsphase die Materie in einem Haufen stark zum Zentrum hin konzentriert ist. Aarseth und andere (1974) [4] geben folgende initiale Verteilung der Dichte an:
bezeichnet dabei die Gesamtmasse, einen die Größe des Systems charakterisierenden Skalenfaktor. Neuere Arbeiten stützen sich auf komplexere Modelle, doch um die wesentlichen Eigenschaften eines Haufens zu demonstrieren, ist dieser einfache Ansatz ausreichend. Nachfolgendes Diagramm zeigt die auf den Zentrumswert normierte Dichte in Abhängigkeit von einem Vielfachen des Skalenfaktors.
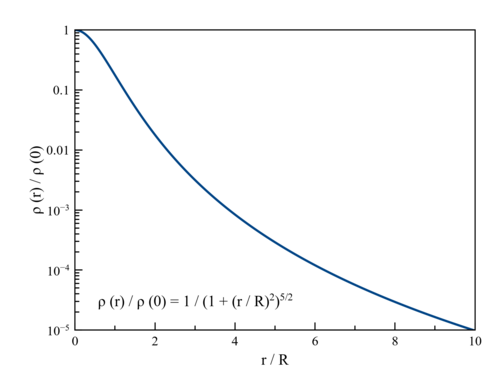
Dem Modell zufolge fällt bereits die Anfangsdichte eines Haufens sehr steil nach außen hin ab. In einer Entfernung vom Zentrum beträgt sie 18%, bei einem Abstand 2% des zentralen Wertes.
Um einzelnen Sternen zufällige Entfernungen zuweisen zu können, ist es besser, anstatt der Verteilung der Dichte diejenige der Masse zu betrachten, welche von einer Kugel mit Radius umschlossen wird. Gemäß dem hier erläuterten Modell lautet diese:
Auch diese Beziehung sei graphisch dargestellt.

Eine Kugel mit Radius enthält demgemäß zu Beginn 35%, eine solche mit einem Radius 72% der Haufenmasse. Um 90% bzw. gar 99% der Gesamtmasse zu erfassen, wird schon zu Anfang ein Abstand von etwa 3.7 bzw. von circa 12.3 benötigt.
Um für ein Mitglied eine zufällige Entfernung vom Zentrum zu definieren, erzeugt man abermals eine Zufallszahl zwischen 0 und 1 und rechnet diese gemäß obiger Massenverteilung in einen Wert um. Da sich diese Beziehung nicht elementar nach der Entfernung auflösen lässt, muss man entweder durch Näherungsmethoden (z.B. das Newton-Verfahren) berechnen oder für verschiedene Werte von als Tabelle vorhalten.
Für Werte von nahe 1 treten sehr große Distanzen auf. Da solche nicht mehr als realistisch betrachtet werden können, empfehlen die Autoren, Werte von größer als 10 nicht mehr zu berücksichtigen. Dies entspricht Zufallszahlen größer als 0.985 entsprechend 98.5% der Haufenmasse.
Um einen vollständigen Satz kartesischer Koordinaten zu erzeugen, muss man in Analogie zum irdischen Gradnetz jedem Stern zusätzlich zur Entfernung zufällige Längengrade zwischen 0 und und Breitengrade zwischen 0 und zuweisen, wobei alle Winkel gleich wahrscheinlich sind. Die Umrechnung dieser Kugelkoordinaten in kartesische geschieht wie folgt:
Einschub für Fortgeschrittene: Anfängliche Dichteverteilung und polytrope Kompression
Das hier angegebene Dichtegesetz lässt sich ableiten, indem man einen Sternhaufen als Ergebnis einer polytropen Kompression im Gravitationsfeld betrachtet. Ein Gas unterliegt einer polytropen Zustandsänderung, wenn zwischen Druck und Volumen bzw. Dichte folgender Zusammenhang besteht. K ist hierbei eine Konstante, der sogenannte Polytropenexponent:
Für eine solche Zustandsänderung existieren mehrere Sonderfälle. Mit = 0 bleibt der Druck konstant, es liegt dann eine isobare Zustandsänderung vor. Im Falle = 1 verhalten sich Druck und Volumen umgekehrt proportional zueinander, was einer isothermen Zustandsänderung entspricht. Wird der Polytropenexponent sehr groß, erkennt man anhand der Umstellung , dass dann das Volumen konstant bleibt, sich also eine isochore Zustandsänderung ergibt.
Für die Energiebilanz während der Kompression ist der Vergleich von mit dem Isentropenexponent entscheidend, welcher durch das Verhältnis der Wärmekapazitäten für isobare und isochore Zustandsänderungen gegeben ist. Ist = , so liegt eine adiabatische Zustandsänderung vor. In diesem Fall tauscht das Gas keine Energie mit seiner Umgebung aus. Für eine durch ihre eigene Gravitation kollabierende Gaswolke gilt < . In solch einem Fall muss man an dem Gas Arbeit verrichten, um diesem Wärme zuzuführen. Dies geschieht hier durch das Gravitationsfeld, in welchem durch die Kontraktion der Gaswolke potentielle Energie in Wärmeenergie überführt wird.
Um diesen Vorgang zu beschreiben, wird der Polytropenexponent oft in der Form geschrieben. Die von Aarseth und anderen (1974) [4] angegebene Dichteverteilung erhält man mit = 5 bzw. = 6/5, was in der Tat geringer als der Isentropenexponent für Wasserstoffgas ist. Ist dieses noch sehr kalt, so dass es in molekularer Form vorliegt, so ist = 7/5. Erhitzt sich der Wasserstoff, so dass die Moleküle in einzelne Atome zerfallen, wird = 5/3.
Allgemein gilt , wobei f die Anzahl der Freiheitsgrade eines Gasteilchens ist. Ein einzelnes Atom hat derer nur 3 entsprechend den 3 möglichen kartesischen Bewegungsrichtungen. Ein zweiatomiges Molekül besitzt zusätzlich 2 Freiheitsgrade der Rotation.
Geschwindigkeitsverteilung
[Bearbeiten]Das Modell von Aarseth und anderen (1974) [4] macht auch Aussagen über die anfänglichen Geschwindigkeiten der Sterne in einem Haufen. Da Sternsysteme aus kollabierenden Gaswolken hervorgehen, darf man annehmen, dass unmittelbar nach dem Ende der Entstehungsphase noch kein Stern sich schneller als die lokale Fluchtgeschwindigkeit bewegt. Die Häufigkeit , mit welcher Geschwindigkeiten zwischen 0 und anzutreffen sind, lautet den Autoren zufolge:
Diese Verteilung ist durch untenstehendes Diagramm wiedergegeben. Der Faktor 23.282074 sorgt dafür, dass die Wahrscheinlichkeit, einen Stern mit beliebiger Geschwindigkeit herauszugreifen, gleich 1 ist. Die Form der initialen Geschwindigkeitsverteilung ist gemäß dem Modell überall im Haufen gleich, auch wenn die Fluchtgeschwindigkeit selbst natürlich vom Abstand zum Zentrum desselben abhängt.

Um die Geschwindigkeitsverteilung durch Zufallszahlen zu simulieren, muss man jetzt etwas trickreicher vorgehen. Man erzeugt zwei Zufallszahlen und zwischen 0 und 1, welche folgende Bedingung erfüllen müssen:
2.146859 ist der maximale Wert, den annehmen kann. Wird die Beziehung nicht eingehalten, muss man solange neue Zahlenpaare generieren, bis diese obiger Anforderung genügen.
Hat man geeignete Zufallszahlen erhalten, so gewinnt man mittels einen zufälligen Geschwindigkeitsbetrag. Um zufällige Bewegungsrichtungen festzulegen, erzeugt man wie für die Positionen zwei zufällige Winkel und , also abermals eine Darstellung in Kugelkoordinaten. Die Umrechnung in kartesische Koordinaten geschieht durch die gleichen Formeln wie schon für die Orte gezeigt.
Die anfänglichen Geschwindigkeiten deuten an, dass ein sehr junger Sternhaufen noch nicht mit einem in thermodynamischen Gleichgewicht sich befindlichen Gas vergleichbar ist. In einem solchen folgen die Teilchen der sogenannten Maxwellschen Geschwindigkeitsverteilung, welche im Gegensatz zum hier skizzierten Modell keine feste obere Schranke für die Geschwindigkeit aufweist, also auch zulässt. Ein junger soeben aus einer kontrahierten Gaswolke entstandener Haufen befindet sich noch weit weg von einem Gleichgewichtszustand, so dass im Laufe seines Lebens signifikante Änderungen nicht nur der Dichte-, sondern auch der Geschwindigkeitsverteilung zu erwarten sind.
Dynamische Entwicklung
[Bearbeiten]Im folgenden sollen anhand eines Systems mit einigen hundert Mitgliedern typische während der Entwicklung eines Sternhaufens auftretende Effekte diskutiert werden. Eine wichtige Voraussetzung dafür ist nicht allein die korrekte Festlegung der Anfangsbedingungen, sondern auch eine adäquate Einstellung des im folgenden benutzten Barnes-Hut-Algorithmus.
Justierung des Barnes-Hut-Algorithmus
[Bearbeiten]Wie im vorausgegangenen Kapitel aufgezeigt, beschleunigt der Barnes-Hut-Algorithmus die Berechnung der auf einen Massenpunkt wirkenden Kraft erheblich, indem Würfel einer Kantenlänge definiert und alle von einem solchen eingeschlossenen Objekte durch ihren Schwerpunkt ersetzt werden. Eine solche Substitution wird als zulässig betrachtet, solange der Abstand eines derartigen Würfels deutlich größer als ist, das Verhältnis also eine vorgegebene Schwelle nicht überschreitet.
Anhand einfacher Konstellationen wurde abgeschätzt, dass der Fehler dieses Näherungsverfahrens für > 0.5 rasch zunimmt. Simulationen mit verschiedenen Werten für zeigen, dass die Energieerhaltung auf lange Sicht bereits für > 0.25 instabil werden kann. Als Beispiel sei ein kleiner Haufen von 100 Sternen mit 0.1 bis 10 Sonnenmassen und einem = 1 Parsec betrachtet, dessen Entwicklung über 35 Millionen Jahre (entsprechend dem 10-fachen seiner Relaxationszeit) verfolgt wird.
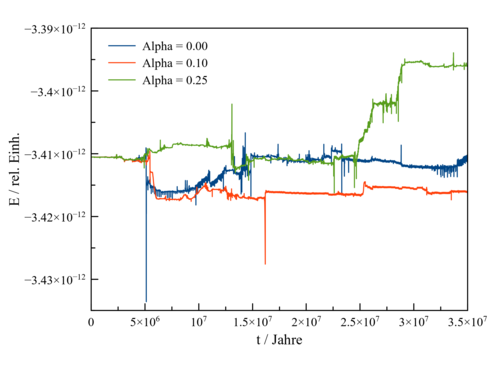
Für = 0, d.h. einen völligen Verzicht auf eine Raumhierarchie, weist die Simulation zumeist eine sehr gute Stabilität der Gesamtenergie auf. Gelegentlich kommt es zu kurzzeitigen Abweichungen, was darauf hindeutet, dass trotz Verwendung adaptiver Zeitschritte und einer Glättung der Gravitation mittels eines Plummerradius enge Begegnungen zweier Massenpunkte nicht immer korrekt behandelt werden. Zudem tritt auch eine langsame Drift der Gesamtenergie auf. Bis auf eine Ausnahme übersteigt der relative Fehler der Gesamtenergie 0.2% nicht.
Auf die Behandlung naher Vorübergänge zweier Haufenmitglieder hat das Einschalten des Bernes-Hut-Algorithmus kaum Einfluss. Mit = 0.1 bzw. 0.25 werden die kurzzeitigen Energieschwankungen weder häufiger noch stärker. Die Drift der Gesamtenergie verstärkt sich jedoch, es werden hier relative Fehler von bis zu 0.3 bzw. 0.5% beobachtet. Mit = 0.5 wird auf lange Sicht die vorliegende Simulation mit relativen Fehlern der Gesamtenergie von mehreren 10% bereits sehr instabil.
Nebst dem Parameter müssen auch die Zeitschritte als Bruchteil der dynamischen Zeitskala festgelegt werden. Das gleiche System wie oben wurde nun mit einem festen = 0.1 modelliert, aber mit verschiedenen Einstellungen für die dynamische Schrittweite. Als Lösungsmethode wurde abermals das Leapfrog-Verfahren herangezogen.

Mit Schritten von 1 / 200 der dynamischen Zeitskala ergibt sich eine sehr gute Energieerhaltung mit einem relativen Fehler von nicht mehr als 0.1%. Wird die Schrittweite auf 1 / 100 gesetzt, wird wie soeben skizziert eine Stabilität der Gesamtenergie auf einem Niveau von 0.3% erreicht. Erhöht man auf 3 / 100 der dynamischen Zeitskala, so verschlechtert sich die Energieerhaltung sowohl hinsichtlich der kurzzeitigen Schwankungen - welche merklich häufiger und intensiver auftreten - als auch der langsamen Drift schon enorm. Der relative Fehler der Gesamtenergie steigt auf bis zu fast 3%. Mit noch gröberen Zeitschritten von 1/10 wird die Gesamtenergie mit relativen Fehlern von erneut mehreren 10% wiederum sehr instabil.
Simulationen mit dem Barnes-Hut-Algorithmus
[Bearbeiten]Die soeben skizzierten Beispiele legen nahe, dass nicht weiter als 0.01 und nicht größer als 0.1 eingestellt werden sollte. Gerade bei kleineren Systemen ist die Anzahl der Massenpunkte pro Würfel oft gering und damit der Barnes-Hut-Algorithmus empfindlich gegenüber der Verteilung der Einzelobjekte innerhalb eines solchen. Der recht kleine Wert für bedeutet andererseits, dass in der näheren Umgebung eines Massenpunktes auf eine Gruppierung der dort vorhandenen Körper verzichtet wird.
Dennoch können damit Systeme einer Größenordnung von mehreren 100 Körpern über mehrere 1-10 Relaxationszeiten hinweg auch auf einem Laptop noch mit annehmbarer Rechenzeit modelliert werden. Die Entwicklung eines solchen Haufens wird nun an einem Ensemble mit 250 Mitgliedern und einer Gesamtmasse von 137 Sonnenmassen sowie einem Skalenradius = 1 Parsec erörtert. Die entsprechende Relaxationszeit beträgt etwa 4.8 Millionen Jahre. Die Simulation erstreckt sich über das 10-fache dieser Zeitskala.
Als erstes sei der zeitliche Verlauf der Energieverhältnisse im Haufen dargestellt. Um die potentielle Energie zu ermitteln, müssen alle möglichen Sternpaare individuell betrachtet werden, d.h. der Aufwand dieser Berechnung ist proportional zu . Um eine zu lange Rechenzeit zu vermeiden, wurde die Energie nicht für jeden Simulationsschritt bestimmt, sondern nur in Zeitabständen von 1/50 von .

liegt zu Beginn der Simulation weit unter 0, d.h. unmittelbar nach der Sternentstehung aus einer sich zusammenziehenden Gaswolke liegt noch kein dynamisches Gleichgewicht vor. Anstatt sich von diesem Anfangswert aus mehr oder weniger asymptotisch 0 anzunähern, schießt das Virial vergleichbar einem Überschwinger zunächst rasch weit darüber hinaus. Erst dann fällt auf langer Zeitskala betrachtet allmählich gegen 0 ab, wobei dieses Abklingen jedoch von sehr heftigen kurzzeitigen Ausschlägen sowohl nach oben als auch nach unten begleitet ist. Der Zeitrahmen dieses Abfalls liegt mit einigen 10 Millionen Jahren deutlich über der aus dem Skalenradius abgeleiteten Relaxationszeit.

Betrachtet man die Energiekomponenten individuell, so findet man in der ersten Phase der Simulation einen erheblichen Abfall der potentiellen Energie, der gemäß der Energieerhaltung von einem äquivalenten Anstieg der kinetischen Energie begleitet ist. Anschließend steigt die potentielle Energie erneut leicht an, entsprechend geht die kinetische Energie wieder etwas zurück. Im weiteren Verlauf der Simulation kommt es immer wieder zu raschen intensiven Umwandlungen der einen in die andere Energieform.
Wie die nächste Abbildung zeigt, ist der anfängliche starke Verlust an potentieller Energie auf eine deutliche Zunahme der Dichte in der Zentralregion des Ensembles zurückzuführen. Um diesen Sachverhalt zu demonstrieren wird wie in der Praxis üblich der Radius betrachtet, welcher die Hälfte der Haufenmasse einschließt. Dieser kontrahiert von etwa 1.46 Parsec ausgehend zunächst rapide und erreicht nach circa 5.3 Millionen Jahren ein Minimum von ungefähr 0.77 Parsec. Danach dehnt sich der Haufen aber zunehmend aus, auch wenn dieser Vorgang mehrfach von Phasen erneuter Kontraktion unterbrochen wird. Nach 22 Millionen Jahren hat erstmals seinen Anfangswert wieder erreicht, am Ende der Modellierung beträgt der Halbmassenradius etwa 1.77 Parsec. Trotz der Expansion sogar über den initialen Wert von hinaus wird das anfängliche Niveau an potentieller Energie nicht mehr erreicht.

Der Eindruck einer anfänglichen Verdichtung und anschließenden Expansion des Haufens wird durch die Verteilung der Entfernungen vom Schwerpunkt bekräftigt. Zum Zeitpunkt maximaler Kontraktion halten sich im innersten Bereich ( < 0.5 Parsec) mehr als doppelt so viele Sterne auf als zu Beginn. Zum Schluss befinden sich dort aber nur noch halb so viele Körper wie am Anfang, wohingegen deutlich mehr Objekte große Abstände von mehr als 2 Parsec aufweisen.
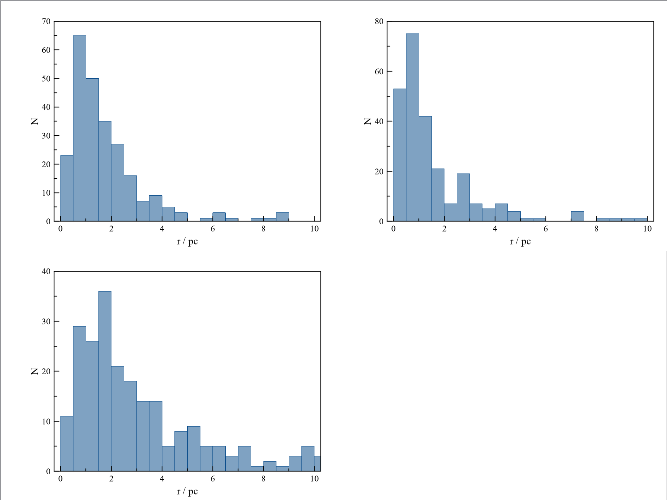
Die Dynamik des Haufens beschränkt sich nicht auf eine Entwicklung der Anzahldichte, sondern umfasst auch die Ausbildung einer
Massenschichtung. Massereiche Objekte konzentrieren sich im Laufe der Zeit zur Mitte hin, während massearme sich bevorzugt am Rand des Systems aufhalten. Trägt man für jeden Stern einzeln seine Masse gegen die Entfernung auf, so erkennt man, dass zum Zeitpunkt stärkster Kontraktion und selbst noch zum Schluss die maximal vorkommende Masse nach außen hin zumeist deutlich abfällt.
Die Massensedimentation sorgt dafür, dass trotz rückläufiger Anzahldichte bis zum Ende die Massendichte im Zentrum hoch bleibt. Dies erklärt, warum es dem Haufen trotz erheblicher Ausdehnung sogar über die Ursprungsgröße hinaus nicht gelingt, die in der anfänglichen Kontraktionsphase verlorene potentielle Energie vollständig zurückzugewinnen.

Der deutliche Anstieg der Dichte im Innenbereich des Haufens nach dessen Entstehung setzt in erheblichem Maße potentielle Energie frei, so dass die anfänglich geringe kinetische Energie stark anwächst - hier auf circa das 3.5-fache des initialen Wertes. Dementsprechend nehmen auch die Geschwindigkeiten der einzelnen Sterne zu - die Höchstwerte um etwa das 2.5-fache. Auch die Form der Geschwindigkeitsverteilung ändert sich. Aus der anfänglich noch relativ symmetrischen wird eine klar schiefe Verteilung, die erst steil ansteigt und danach mit einem ausgeprägten Schwanz langsam zu hohen Geschwindigkeiten hin abfällt. Genau das ist auch für die Geschwindigkeiten der Moleküle in einem Gas typisch.

Sehr aufschlussreich ist schließlich auch die Gegenüberstellung von Geschwindigkeit und Entfernung. Ganz zu Anfang ist (abgesehen von der Beschränkung der Höchstgeschwindigkeit auf die Fluchtgeschwindigkeit) noch kein Trend sichtbar. Zur Zeit maximaler Zentraldichte liegt jedoch ein sehr starkes Gefälle vor. Bis auf wenige Ausnahmen zeigen die Sterne mit zunehmendem Abstand vom Schwerpunkt immer geringere Geschwindigkeiten, wie man das für an ein Schwerezentrum gebundene Objekte aber auch erwartet. Bis zuletzt bleibt diese Geschwindigkeitsschichtung sehr präsent. Zugleich treten jenseits von etwa 6 Parsec jedoch auch Körper auf, deren Geschwindigkeit mit zunehmender Entfernung zu- anstatt abnimmt.
Die im dichten Zentrum sich aufhaltenden Sterne laufen auf chaotischen Bahnen weitgehend regellos wie die Moleküle in einem Gas. In mittlerer Entfernung kann man die Orbits als allerdings stark gestörte Ellipsen betrachten. Die am Rand mit abnorm hoher Geschwindigkeit sich bewegenden Objekte weisen Hyperbelbahnen auf, sind nicht mehr an das Ensemble gebunden. Es handelt sich um Sterne, die durch enge Passagen mit einem zweiten Haufenmitglied stark beschleunigt und so aus dem System herausgeschleudert wurden. Je höher die Geschwindigkeit nach einer solchen Beinahekollision ausfällt, umso mehr kann der betroffene Körper während einer gewissen Zeit sich vom Zentrum entfernen.

Trotz aller für die Simulation benutzen Näherungen (Glättung der Gravitation durch Plummerradius, Zusammenfassung mehrerer Massenpunkte gemäß des Barnes-Hut-Algorithmus) handelt es sich bei solchen Hinauswürfen um realistische Vorgänge, die wiederum den Vergleich mit einem Gas zulassen. So können z.B. einzelne Gasmoleküle der Erdanziehungskraft entkommen, wenn sie nach Stößen untereinander zufällig stark vom Erdmittelpunkt weg beschleunigt werden. So wie überwiegend massearme Sterne aus einem Haufen entweichen, verliert die Erde vor allem leichte Moleküle, weshalb nach der Erdentstehung noch vorhandene leichte Elemente wie Wasserstoff und Helium längst in den Weltraum entkommen sind.
Das "Verdampfen" einzelner Mitglieder sorgt dafür, dass Sternhaufen im Laufe der Zeit sich von selbst auflösen. Laut Röser und Tscharnuter (2012) [5] beläuft sich der Verlust pro Relaxationszeit auf 0.7 % der ursprünglich vorhandenen Sterne. Im vorliegenden Beispiel sollten nach 10 Relaxationszeiten 7% aller Körper (18 von 250) davon betroffen sein. Obiges Diagramm erweckt den Eindruck, dass trotz der Glättung der Anziehungskraft mit einem Plummerradius und der Verwendung dynamischer Zeitschritte die Anzahl dem System verlustig gegangener Mitglieder etwas überschätzt wird - sie liegt hier mit 25 Haufenmitgliedern bei 10%.
Besondere Effekte
[Bearbeiten]Obwohl von einfachen Simulationen vorhergesagte Vorgänge in Sternhaufen wie die Verdichtung der Zentralregion durch eine dort zunehmende Konzentration massereicher Sterne oder das Entkommen einzelner Mitglieder infolge von Beinahekollisionen mit jeweils einem zweiten Stern in der Natur tatsächlich beobachtet werden, können solche Modelle nur als grobe Wiedergabe der Realität betrachtet werden. Tatsächlich lassen sie viele Details außer acht, die einen erheblichen Einfluss auf die dynamische Entwicklung von Haufen ausüben und so für eine korrekte quantitative Beschreibung unerlässlich sind.
Endliche Ausdehnung der Sternkörper
[Bearbeiten]Bislang wurden in diesem Buch Himmelskörper ausnahmslos als Massenpunkte betrachtet. Tatsächlich aber weisen solche natürlich eine endliche Ausdehnung auf. Kommen sich zwei Körper bis auf einen Abstand nahe, der nicht mehr sehr groß im Vergleich zu ihren eigenen Abmessungen ist, dürfen diese nicht mehr als punktförmig behandelt werden. Wie man es von Erde und Mond kennt, üben sie dann erhebliche Gezeitenkräfte aufeinander aus, was anhand folgender Abbildung erläuert werden soll.
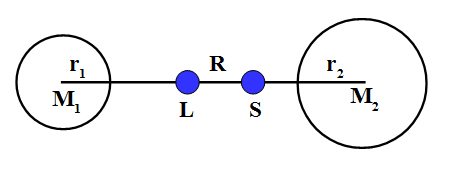
Man betrachte zwei Massen und mit Radien und , die sich bis auf einnen Abstand genähert haben. Ein Teilchen, das sich im Mittelpunkt von befindet, erleidet dann durch eine Beschleunigung . Sitzt das Teilchen jedoch ganz rechts an der Oberfläche von , so liegt wegen der geringeren Entfernung zu eine größere Beschleunigung vor. Umgekehrt spürt man ganz links auf infolge eines größeren Abstandes zu eine verminderte Beschleunigung . Solange die Radien der sich begegnenden Sterne noch relativ klein im Vergleich zu ihrem Abstand sind, darf man die Näherungen und benutzen. Für die Beschleunigungsdifferenz zwischen Mittelpunkt und Oberfläche von ergibt sich damit:
Analog gilt für die Beschleunigungsdifferenz auf :
Ausgedehnte Körper in einem Doppelsystem spüren nicht nur unterschiedliche Anziehungskräfte durch ihren jeweiligen Partner, sondern auch verschiedene Fliehkräfte infolge der Bahnbewegung um ihren gemeinsamen Schwerpunkt S. Nur an den Mittelpunkten der beiden Massen halten Fliehkraft und Schwerkraft einander die Waage. Auf den (jeweils dem anderen Stern zugewandten) Vorderseiten liegen unterdurchschnittliche Zentripetalkräfte vor, welche die überdurchschnittlichen Schwerkräfte nicht kompensieren können. Dementsprechend bilden sich dort Erhebungen aus, welche völlig den irdischen Flutbergen entsprechen. Auf den Rückseiten ist die Kraftbilanz genau umgekehrt. Zu große Fliehkräfte treffen auf zu kleine Anziehungskräfte, so dass auch dort Erhebungen entstehen, welche den vorderseitigen genau entgegengesetzt sind.
Die auf einen Körper endlicher Ausdehnung wirkende Beschleunigungsdifferenz und damit Gezeitenkraft ist direkt proportional zu seinem Radius und umgekehrt proportional zur 3. Potenz der Distanz zu seinem Partner. Kommen sich zwei Sterne bis auf einen Abstand von nur noch wenigen ihrer eigenen Radien nahe, so kann die Gezeitenkraft fast das Niveau der gegenseitig ausgeübten Schwerkraft erreichen. In den sehr dichten Zentren von Kugelhaufen treten derartige Beinahezusammenstöße tatsächlich mit signifikanter Häufigkeit auf.
Wird ein Körper durch Gezeiten verformt, entsteht Wärme, wofür im Sonnensystem eindrucksvolle Beispiele wie der Jupitermond Io existieren. Die dafür erforderliche Energie wird der Bahnbewegung entnommen, wodurch die Gesamtenergie definiert als Summe von kinetischer und potentieller Energie nicht mehr konstant ist, sondern vielmehr abnimmt.
Bei sehr engen Vorübergängen laufen Sterne häufig auf Hyperbeln, deren Exzentrizität nur wenig über 1 liegt. Dann reicht schon ein geringer Energieentzug aus, um die Orbits in langgestreckte Ellipsen mit einer Exzentrizität von knapp unter 1 zu verwandeln. Wie verschiedene sehr detaillierte Simulationen (z.B. von Mardling (1995) [6]) gezeigt haben, reicht bei einer Mindestentfernung von wenigen Sternradien die von einer Hyperbelbahn nur einmal gebotene Chance in der Tat aus, um durch gezeitenbedingten Energieverlust ein gebundenes Doppelsternsystem zu bilden.
Diese Art des Einfangs sowie die darauffolgende Entwicklung des neuen Doppelsystems stellen äußerst komplexe Prozesse dar. Man muss die Verformung der Sternköper durch ein hydrodynamisches Modell genau berücksichtigen, um die daraus resultierende Umwandlung von Bahnenergie in Wärme korrekt zu bestimmen. Die Verformung wirkt zudem nicht nur durch Energieentzug, sondern auch eine modifizierte Gravitation auf die Bahnen zurück. Die Massenverteilungen innerhalb der Körper sind während der Begegnung nicht mehr kugelsymmetrisch, so dass diese zur Berechnung der gegenseitigen Anziehungskräfte nicht mehr durch ihre Massenmittelpunkte ersetzt werden dürfen.
Erschwerend kommt hinzu, dass ein Stern nicht beliebig verformbar ist. Ein Flutberg kann maximal bis zum sogenannten 1. Librationspunkt L aufsteigen, an welchem die von den beiden Massen und ausgeübten Gravitationskräfte sich exakt einander aufheben. Ein Teilchen, das sich an dieser Stelle befindet, fällt bei der geringsten Störung auf seinen Ursprungskörper zurück, oder auf den Partner, oder entkommt sogar ganz dem System. Bei einer Beinahekollision ist vor allem der Partner mit dem größeren Volumen von derart ausgedehnten Erhebungen betroffen. Er verliert dadurch Masse, teils an seinen Begleiter, teils an den Weltraum. Erstrecken sich auch auf dem kleineren Stoßpartner Flutberge bis zu L, berühren sich dort sogar die beiden Sterne.
Mardling (1995) [6] zeigte, dass das Geschehen nach der Einfang sich in zwei Stadien unterteilen lässt. Die erste Phase ist, da die Körper auf sehr exzentrischen Ellipsen umlaufen, von wiederholten engen Passagen und dementsprechend starken Verformungen und Energieverlusten gekennzeichnet. Die Bahnen sind chaotisch (d.h. sehr empfindlich gegenüber Störungen) und starken raschen Veränderungen unterworfen. So kann z.B. die Exzentrizität um einige 0.1 auf einer Skala von nur wenigen 10-100 Umläufen variieren, wobei die Umlaufsperiode u.U. nur in der Größenordnung von Tagen oder gar Stunden liegt. Wiederholt kommt diese dabei nahe an 1 heran, so dass schon eine geringe Störung die Bahn wieder in eine Hyperbel umwandeln, d.h. das System wieder trennen kann. Umgekehrt kann der Mindestabstand derart gering werden, dass die beiden Sterne fast direkt miteinander kollidieren und infolgedessen zu einem einzigen Körper verschmelzen.
Sofern das Doppelsternsystem den chaotischen Beginn übersteht, schließt sich nach typischerweise mehreren 100-1000 Umläufen ein stabiles Stadium an, währenddessen die elliptischen Orbits sich mehr und mehr Kreisbahnen annähern, auf denen beide Mitglieder sich stets die gleiche Seite zukehren (deren Rotationsperiode entspricht dann der Bahnperiode, was als gebundene Rotation bezeichnet wird). Auf elliptischen Bahnen sind die Körper weiterhin wegen der wechselnden Abstände voneinander permanenten Formänderungen unterworfen, wodurch nach wie vor, wenn auch im Vergleich zum ersten Stadium geringe Energieverluste pro Umlauf auftreten. Auch auf Kreisbahnen entziehen die Gezeiten dem Doppelsystem Energie, solange Rotation und Bahnumlauf noch nicht im Takt sind. Zwar ändert sich dann nicht mehr die Höhe der Flutberge, doch laufen diese noch periodisch um die Oberflächen der Körper herum (wie dies auch bei den irdischen Gezeiten für die Erde noch der Fall ist). Erst wenn zusätzlich zur Kreisbahn eine gebundene Rotation vorliegt, bleiben die Formen der beiden Körper stabil, so dass der Energieverlust zum Stillstand kommen kann. Dieses Abklingstadium dauert sehr viel länger als die chaotische Anfangsphase, es erstreckt sich üblicherweise über 1-10 Millionen Jahre.
Am Ende liegt ein sehr enges Doppelsystem vor, dessen Bahnen eine Ausdehnung von nur wenigen Sternradien aufweisen. Von den übrigen Mitgliedern des Haufens aus betrachtet, kann man dieses als einen einzigen Körper betrachten (d.h. anstelle der beiden Massen und eine einzige Punktmasse am Schwerpunkt S annehmen), sofern sich nicht ein dritter Stern den beiden Körpern nähert.
Die Entstehung und Entwicklung von Doppelsternsystemen infolge von Gezeiten ist viel zu komplex, als dass man jedes derartge Ereignis im Verlauf einer Sternhaufensimulation im Detail berücksichtigen könnte. Mardling und Aarseth (2001)[7] konnten durch eine Vielzahl von Doppelsternsimulationen und theoretische Überlegungen jedoch handliche Regeln ableiten, mit welchen die Dauer des chaotischen Stadiums, der dabei auftretende Energieverlust und die am Ende dieser Phase vorliegenden Bahnelemente in Abhängigkeit von den Massen der Stoßpartner, ihrem Minimalabstand und der dabei herrschenden Relativgeschwindigkeit ausreichend genau abgeschätzt werden können. Ebenso kann anhand solcher Faustregeln auch die zweite Phase mit akzeptabler Genauigkeit verfolgt werden.
Primordiale Doppelsterne und Dreierstöße
[Bearbeiten]Die meisten Doppelsterne bilden sich nicht durch Beinahezusammenstöße von Einzelsternen, sondern bereits während der Entstehung eines Haufens aus einer sich zusammenziehenden Gaswolke. Einzelne Teilwolken können aufgrund ihrer im Vergleich zu fertigen Sternen viel größeren Abmessungen viel leichter sich einander begegnen und dadurch gravitativ gegenseitig binden. Ein Sternhaufen weist somit von Anfang an einen gewissen Anteil von Doppelsystemen auf, welche dementsprechend als primordial bezeichnet werden.
Bedingt durch die Entstehung aus großen Teilwolken sind die Orbits solcher Doppelsterne viel ausgedehnter als für nachträglich aus Gezeiteneinfang hervorgegangene Systeme - typischerweise weisen sie die gleichen Dimensionen auf wie die Bahnen der Planeten und Kleinplaneten in unserem Sonnensystem. Dies bedeutet aber, dass vor allem im dichten Zentrum eines Haufens nahe Vorübergänge eines dritten Sterns an einem Doppelsystem (d.h. mit einem Mindestabstand, der nicht mehr sehr groß im Vergleich zum Abstand der beiden Partner untereinander ist) recht häufig sind. Es liegt dann eine Begegnung von drei Massen zumeist gleicher Größenordnung vor, bei welcher die dritte Masse das Doppelsystem erheblich stört. Schließlich können selbst zwei Doppelsterne aufeinander treffen, wobei die beide Systeme sich massiv gegenseitig beeinflussen.
Detaillierte Untersuchungen zeigen, dass solche Dreier- und Viererstöße die Struktur eines Haufens deutlich modifizieren. Um derartige Ereignisse nicht mit sehr kleinen dynamischen Zeitschritten behandeln zu müssen, sind insbesondere für Dreierstöße Lösungsverfahren entwickelt worden, welche wie die Berechnung der Planetenbahnen auf dem gestörten Zwei-Körper-Problem beruhen. Während die Bahn eines Planeten jedoch fast völlig durch die überwältigende Masse der Sonne dominiert wird, steht einem Doppelsternsystem bei einem Dreierstoß ein gleichwertiger Störer gegenüber, so dass die Behandlung dieses Problems wesentlich schwieriger ist.
Ein möglicher Weg zur Beschreibung einer Dreierbegegnung ist die Verwendung eines hierarchischen Koordinatensystems, wie Mardling (2001) [8] diskutiert hat. Die untere Ebene ist durch den Doppelstern repräsentiert, dessen beide Komponenten untereinander den Abstand und die Relativgeschwindigkeit aufweisen. Die Bewegung des dritten Sterns wird relativ zum Schwerpunkt des Doppelsystems betrachtet. Er weist einen Abstand und eine Geschwindigkeit in Bezug auf diesen auf, bildet also zusammen mit die obere Ebene. Ein dritter Koordinatensatz ist nicht erforderlich - der Schwerpunkt des gesamten Dreierensembles wird einfach unbeweglich in den Koordinatenursprung gesetzt.

Physikalisch bedeutet diese Koordinatenwahl, das Drei-Körper-System als eine Überlagerung von zwei gestörten Zwei-Körper-Systemen aufzufassen. Der Doppelstern wird durch den dritten Körper gestört. Umgekehrt wird dieser gestört, weil die beiden Mitglieder des Doppelsystems eben nicht in ihrem Schwerpunkt vereint, sondern räumlich voneinander getrennt sind.
Nebst dieser Zurückführung des Drei-Körper-Problems auf zwei gestörte Zwei-Körper-Probleme nutzt die Autorin für ihr Lösungsverfahren auch charakteristische Phänomene von Dreierbegegnungen aus. Um solche zu veranschaulichen, genügt erneut eine Standardmethode wie das Hermite-Polynome-Verfahren. Als Beispiel sollen im Folgenden drei Sterne von je 1 Sonnenmasse dienen, die sich zu Beginn an den Positionen (10 AE / 0 / 0), (-10 AE / 0 / 0) und (1000 AE / 0 / 0) befinden. Die Ausgangsgeschwindigkeiten betragen (0 / 5 km/s / 0), (0 / -5 km/s / 0) und (0 / 0.5 km/s / 0.1 km/s). Die dynamische Schrittweite wird auf 0.5% des Verhältnisses Beschleunigung / Ruck gesetzt.
Solange der dritte Stern sich weit entfernt vom Doppelsystem aufhält, bleiben dessen Bahnelemente stabil (die in untenstehenden Diagrammen auf den Relativkoordinaten beruhen). Mit zunehmender Annäherung dieses Stoßpartners - er kommt an den Schwerpunkt des Doppelsterns bis auf etwa 60 AE heran - unterliegen diese aber immer stärkeren quasiperiodischen Oszillationen. Ein Vergleich mit den Störungen der Planetenbahnen in unserem Sonnensystem zeigt, dass die bei einem Dreierstoß ebenbürtiger Massen auftretenden Schwankungen sehr viel heftiger ausfallen. Während die großen Halbachsen der Planetenorbits sich über Äonen kaum ändern, variiert im vorliegenden Beispiel dieser Parameter für das Doppelsystem um etwa 10% seines Absolutwertes in nur wenigen Jahrzehnten, wobei der Orbit letztendlich von etwa 23 AE auf 21 AE schrumpft. Ebenso abrupt steigt die Exzentrizität der Bahn von etwa 0.11 auf 0.36. Im Sonnensystem hingegen vergehen selbst bei den massearmen inneren Planeten Jahrtausende, ehe sich die Exzentrizität auch nur um 0.01 ändert.
Noch dramatischer wirkt sich die enge Begegnung auf den Orbit des dritten Körpers auf (was hier nicht graphisch dargestellt ist). Dessen große Halbachse beträgt zunächst etwas mehr als 500 AE, liegt aber nach dem Stoß bei fast 3600 AE, d.h. die Bahn weitet sich enorm. Zugleich wächst deren Exzentrizität von etwa 0.90 auf fast 0.99.


Die Störung des Doppelsterns und diejenige des Stoßpartners sind komplementär zueinander. Sie treten einander in Resonanz wie häufig auch die Planeten des Sonnensystems, tun dies jedoch ungleich stärker. Genau an dieser Resonanzeigenschaft setzt Mardling (2001) [8] an.
Erklären lässt sich die intensive Resonanz durch einen erheblichen Energieaustausch zwischen dem Doppelsystem und seinem Störer. Die durch eine Kepler-Bahn repräsentierte Energie ist umgekehrt proportional zu deren großen Halbachse , denn es gilt:
bezieht sich erneut auf die Relativbewegung der beiden Massen und . Die geschrumpfte Bahn des inneren Doppelsterns bedeutet also, dass dieser Energie verloren hat. Der Stoßpartner geht aus dem Ereignis mit einem ausgedehnteren Orbit hervor entsprechend einem Gewinn an Energie.
Dieser Energietransfer von Doppelsystem zu Störer ist für Dreierbegegnungen charakteristisch, wie z.B. von Heggie und anderen (2006) [9] erörtert wurde. Er verleiht Einzelsternen, die Doppelsysteme passieren, mehr Energie. Verwendet man abermals das Vergleichsbild des Gases, entspricht dies einer Aufheizung, welche der Gravitation entgegenwirkt. Die Verdichtung der Zentralregion wird durch das Vorhandensein primordialer Doppelsterne abgeschwächt.
Die Mitnahme von Energie durch einen Stoßpartner kann (wie der Gezeitenanfang) nachträglich Doppelsterne entstehen lassen. Kommen sich zwei Körper auf einer Hyperbelbahn mit einer Exzentrizität von nur wenig über 1 nahe, reicht eine relativ geringfügige Störung durch einen dritten Stern aus, diese auf einer langgestreckten Ellipse aneinander zu binden.
Obige Autoren weisen jedoch daraufhin, dass andererseits viele Doppelsysteme im Laufe der Zeit durch enge Passagen eines dritten Sterns oder gar eines anderen Doppelsterns zerstört werden. Liegt schon vor solch einer Begegnung eine stark exzentrische Bahn vor, so reicht eine kurzzeitige Energiezufuhr aus, um die Komponenten des Doppelsystems voneinander zu trennen. In einem solchen Fall jedoch erleidet der Stoßpartner einen Energieverlust, was gemäß der Metapher des Gases eine Abkühlung und damit einen Trend hin zu einer stärkeren Verdichtung bedeutet.
Einschub für Fortgeschrittene: Mathematische Beschreibung eines Dreierstoßes
Die von Mardling (2001) [8] eingeführten Relativvektoren und zur Aufteilung des Dreikörperproblems in ein inneres und äußeres Zweikörperproblem stellen Jacobi-Koordinaten dar, wie sie auch im Verfahren von Wisdom und Holman (1991) [10] zur Berechnung der Planetenbahnen benutzt werden. Ebenso wie für jene Autoren stellen auch für Mardling die Hamilton-Funktion und die daraus abgeleiteten Hamiltonschen Gleichungen die Grundlage der Lösung dar.
Die Hamilton-Funktion besteht nun aus einer inneren Komponente und einer äußeren . ist durch die Relativbewegung der beiden inneren Massen und zueinander gegeben:
Komplizierter verhält es sich mit . Der kinetische Anteil ist durch die Bewegung der Masse relativ zum Schwerpunkt der beiden inneren Körper gegeben. Um die potentielle Energie korrekt zu beschreiben, müssen aber die exakten Abstände von zu und genommen werden. Diese können jedoch auf und zurückgeführt werden. Die inneren Massen weisen von ihrem Schwerpunkt die Entfernungen und auf. Somit hat der äußere Körper einen Abstand zu und einen solchen zu ( soll dabei von der 1. zur 2.Masse zeigen). Aus alledem ergibt sich:
Vergleichbar dem Problem der Planetenbahnen, muss auch jetzt die Hamilton-Funktion in ungestörten Anteil und Störfunktion aufgeteilt werden. Diese Trennung muss sowohl für als auch vorgenommen werden.
Für die Zerlegung der inneren Hamilton-Funktion betrachtet die Autorin den Betrag des Relativvektors sowie die Winkelgeschwindigkeit auf der relativen Umlaufbahn und benutzt den Ansatz sowie . und beschreiben die ungestörte Bewegung, und die Störung derselben. Wie Wisdom und Holman für die Planetenbahnen geht Mardling für den Dreierstoß davon aus, dass mit genügend klein gehaltenen Zeitschritten die Störung als klein im Vergleich zur ungestörten Bewegung angenommen werden darf. Unter dieser Voraussetzung darf als Taylorreihe um und entwickelt und diese Darstellung nach den linearen Gliedern abgebrochen werden.
Der entscheidende Unterschied zwischen dem Planetenproblem und dem Dreierstoß liegt in der Behandlung der Störfunktion. Bei ersterem ist die Störung so gering, dass diese wie schon erläutert durch kleine periodische Stöße modelliert werden darf, und so als Delta-Funktion nur zu diskreten Zeitpunkten in der Hamilton-Funktion auftaucht, ansonsten aber auf 0 gesetzt bleibt. Im Falle des Dreierstoßes aber muss die viel stärkere Störung als permanent betrachtet werden. Dem quasiperiodischen Verhalten der Bahnelemente des inneren Systems Rechnung tragend, behandelt Mardling die Störung als Überlagerung harmonischer Schwingungen:
und stellen die zeitabhängigen Amplituden dar, mit welchen der Relativabstand und die relative Winkelgeschwindigkeit der beiden inneren Massen um die ungestörten Größen oszillieren. Man beachte dabei, dass die Fourierentwicklung nicht nach der Zeit, sondern dem Polarwinkel erfolgt. Die Autorin stellt die Störung des inneren Systems somit als Überlagerung stehender Wellen dar. Das Schwingungsmuster ist gleichwohl nicht stationär, da die Amplituden sich zeitlich verändern und nicht nur der Relativabstand, sondern auch die relative Winkelgeschwindigkeit an der Oszillation teilhat.
Um die äußere Hamilton-Funktion zu separieren, fügt man das Glied ein und zieht es wieder ab:
Die beiden ersten Terme geben die ungestörte Bewegung von relativ zu wieder. Die nachfolgenden Terme geben die Störung an, welche die äußere Masse erleidet, weil die beiden inneren Körper räumlich voneinander getrennt sind. Man kann sie als Gezeitenkraft interpretieren, welche inneres und äußeres Systems aufeinander ausüben.
Durch ihre räumliche Trennung erscheinen die inneren Komponenten der äußeren als Dipol, welcher jedoch sich selbst und seine Lage relativ zu fortlaufend ändert. Dies hat zur Folge, dass der äußere Körper effektiv eine Überlagerung von Multipolen spürt. Dies führt zu dem Ansatz:
Hierbei ist . Die stellen die sogenannten Kugelflächenfunktionen dar.
Wegen der komplizierten Störfunktionen und der Verschränkung zweier gestörter Zweikörperprobleme ist die mathematische Behandlung einer Begegnung von drei ebenbürtigen Massen viel schwieriger als diejenige einer nur leicht gestörten Planetenbahn. Trotz aller hier getroffenen Vereinfachungen ist das Problem des Dreierstoßes oft nicht geschlossen lösbar. Mardling hat die Voraussetzungen einer solchen Lösbarkeit detailliert untersucht und festgestellt, das Resonanzen zwischen innerem und äußerem System dabei eine fundamentale Rolle spielen.
Entwicklung der Sterne
[Bearbeiten]Schließlich muss bei der Simulation eines Haufens berücksichtigt werden, dass die Sterne sich auch als Einzelobjekte im Laufe der Zeit verändern. Massereiche Sterne sind viel leuchtkräftiger als massearme, so dass sie ihren Wasserstoffvorrat in viel kürzerer Zeit aufbrauchen. Die Leuchtkraft eines Hauptreihensterns ist etwa proportional zur dritten Potenz seiner Masse, so dass seine Lebensdauer ungefähr umgekehrt proportional zum Quadrat derselben ist. Während ein sonnenähnlicher Körper etwa 10 Milliarden Jahre lang durch Kernfusion Energie gewinnen kann, kommt ein Stern mit 10 Sonnenmassen nur etwa 100 Millionen Jahre über die Runden. Die massereichsten Sterne - solche weisen mehr als 100 Sonnenmassen auf - überdauern gar nur etwa 1 Million Jahre. Die masseärmsten roten Zwerge, welche nur knapp 0.1 Sonnenmassen besitzen, weisen hingegen eine Lebenserwartung von etwa 1 Billion Jahren auf.
Geht im Kern eines Sterns die Energieerzeugung durch Fusion von Wasserstoff zu Helium zu Ende, beginnt sich dessen innere Struktur dramatisch zu verändern. Während die Zentralregion sich verdichtet, bis schließlich Helium zu Kohlenstoff fusionieren kann, dehnen sich die äußeren Schichten aus. Der Stern wird je nach seiner Ausgangsmasse zum Roten Riesen oder gar Überriesen. Wegen der soeben erwähnten Masse-Leuchtkraft-Beziehung können seit der Entstehung des Universums jedoch selbst die ältesten Sterne mit weniger als etwa 0.8 Sonnenmassen das Riesenstadium überhaupt noch nicht erreicht haben.
Bläht sich ein Stern zum (Über)riesen auf, so wird seine gravitativ nur noch schwach gebundene Hülle instabil. Er verliert einen signifikanten Teil seiner Masse durch sogenannte Sternwinde. Die Ausströmungsgeschwindigkeit liegt zumindest in der Größenordnung von 10 km/s und damit in der Regel deutlich über der Fluchtgeschwindigkeit in einem Haufen, so dass die abgegebene Materie dem Ensemble entkommt. Sehr massereiche Sterne (mit mehr als circa 8 Sonnenmassen) enden als Supernova, wenn nach dem Ende der Überriesenphase nach einigen weiteren Zwischenschritten mit Kernfusionen bis hin zum Eisen die thermonukleare Energiequelle endgültig versiegt. Der Kern kollabiert dabei zu einem Neutronenstern oder gar einem Schwarzen Lock, während zugleich die Hülle durch eine ungeheure Explosion abgestoßen wird. Die Auswurfgeschwindigkeit ist mit einer Größenordnung von 1000 km/s extrem hoch, so dass dieses Material einen Haufen schon in wenigen Jahrtausenden verlässt. Mit den Einzelobjekten verlieren also auch Sternhaufen an Masse, wobei sie vor allem die massereichen Sterne bis auf die zurückbleibenden Neutronensterne und Schwarzen Löcher rasch einbüßen.
Die Entwicklung eines Sterns wird erheblich modifiziert, wenn er einem engem Doppelsystem angehört. Beginnt er sich am Ende seines Lebens zum (Über)riesen auszudehnen, unterliegt er mehr und mehr der von seinem Partner ausgehenden Gezeitenkraft. Erstreckt er sich schließlich bis zum 1. Librationspunkt, beginnt er an dieser Stelle Masse zu verlieren und seine Aufblähung wird gestoppt. Dieser Massenverlust senkt die Leuchtkraft des Sterns und wirkt somit lebensverlängernd. Zugleich weitet sich infolge der schwächer werdenden Anziehungskraft der Orbit des Doppelsterns. Eine solche Expansion der Bahn tritt selbstverständlich auch dann auf, wenn ein Partner durch Sternwind anstatt gezeitenbedingter Verformung Masse verliert.
Endet ein Mitglied eines Doppelsystems als Supernova, so wird dieses durch den abrupten enormen Massenverlust zumeist zerstört. Der zurückbleibende Neutronenstern bzw. das Schwarze Loch und der Begleitstern fliegen oft mit hoher Geschwindigkeit auseinander und entkommen dem Gesamtsystem.
Ein zum (Über)riesen gewordener Stern kann wiederum viel leichter einen Beinahezusammenstoß mit einem zweiten Stern erleiden als ein Hauptreihenobjekt. Dem steht jedoch gegenüber, dass das (Über)riesenstadium etwa um eine Größenordnung kürzer ist die Verweildauer auf der Hauptreihe.
Die Entwicklung der Zustandsgrößen der Sterne im Laufe der Zeit - für ein Mehrkörperproblem sind vor allem Masse und Radius von zentraler Bedeutung - ist in zahlreichen Datenbanken in Abhängigkeit von der Anfangsmasse, der chemischen Zusammensetzung und anderen Parametern wie etwa der Rotationsgeschwindigkeit tabelliert. Entwicklungseffekte können daher zumeist mit nicht allzugroßem Aufwand in die Simulation eines Haufens eingebaut werden, zumindest solange man es nicht mit durch Gezeitenkräfte stark gestörten engen Doppelsternen zu tun hat. Allerdings beruhen diese Tabellen z.T. auf unterschiedlichen Modellen, welche sich vor allem hinsichtlich der Spätstadien nach der Hauptreihenphase unterscheiden.
Beispiel einer detaillierten Simulation
[Bearbeiten]Als Beispiel einer Simulation, welche all die soeben geschilderten Effekte berücksichtigt, sei eine Arbeit von Giersz und Heggie (2011) [11] zitiert. Die Autoren versuchten mehrere große Haufen der Milchstraße zu modellieren, unter anderem 47 Tucanae. Um die Ergebnisse der Simulationen letztendlich mit Beobachtungen vergleichen zu können, gingen sie wie folgt vor.
Räumliche Dichteverteilungen innerhalb eines Sternsystems lassen sich nicht direkt beobachten. Sofern die einzelnen Mitglieder noch als voneinander getrennt beobachtet werden können, lässt sich durch die bereits erwähnte Methode der Sternzählung zumindest noch exakt ermitteln, wie viele Objekte pro Flächeneinheit auf der Ebene senkrecht zur Blickrichtung zu liegen scheinen. Ist dies nicht möglich, wie etwa für die extrem dichten Zentren von Kugelsternhaufen, muss man die Anzahl der auf ein Flächenstück fallenden Sterne anhand der Helligkeit desselben abschätzen. Dies wiederum setzt allerdings voraus, dass die Häufigkeit bekannt ist, mit welcher Sterne einer bestimmten Helligkeit vertreten sind. Da alle Mitglieder eines Haufens (abgesehen von nicht dazugehörenden Sternen im Vorder- oder Hintergrund) die gleiche Entfernung aufweisen, kann für die in Einzelsterne auflösbaren Bereiche eine solche Häufigkeitsverteilung jedoch mit hoher Genauigkeit ermittelt werden.
Auch Geschwindigkeiten lassen sich in der Regel nicht in voller Räumlichkeit erfassen. Wie schon in diesem Kapitel angedeutet, sind insbesondere Bewegungen senkrecht zur Blickrichtung ab einer gewissen Entfernung nicht mehr nachweisbar, wohingegen die Geschwindigkeit parallel zur Blickrichtung dank des Dopplereffekts für beliebig ferne Himmelskörper ermittelt werden kann. Dies setzt wiederum voraus, dass das Objekt als Individuum sichtbar (und für spektrale Beobachtungen noch genügend hell) ist. Besteht das für die Geschwindigkeitsmessung erforderliche Spektrum aus dem aufsummierten Licht vieler Sterne, kann man für deren Bewegungen nur statistische Größen angeben, z.B. den Mittelwert und die Streuung der Geschwindigkeiten.
Die für die Sonnenumgebung ermittelte Häufigkeit bestimmter Sternmassen lässt sich nicht ohne weiteres auf andere Systeme übertragen. Die Sterne von Kugelhaufen weisen im Vergleich zur solchen der galaktischen Scheibe einen deutlich geringeren Anteil von Elementen jenseits des Wasserstoffs und Heliums auf, was den Prozess der Sternentstehung und damit die Häufigkeit von Sternmassen signifikant beeinflusst. Die Autoren haben mehrere Simulationen mit plausiblen Massenverteilungen durchgeführt und deren Verlässlichkeit anhand der vorhergesagten Dichte- und Geschwindigkeitsverteilungen verifiziert. Sie kommen damit zum Schluss, dass 47 Tucanae von Anfang an vergleichsweise wenig massereiche Sterne aufwies - im Bereich zwischen 0.8 und 50 Sonnenmassen lag unmittelbar nach Entstehung des Haufens eine Häufigkeitsverteilung vor, wohingegen in der Sonnenumgebung gegeben ist. Der Anteil sehr massearmer Sterne war im Vergleich zu unserer Milchstraßenregion jedoch ebenfalls schon zu Beginn an unterdurchschnittlich. Giersz und Heggie geben für 47 Tucanae im Bereich zwischen 0.08 und 0.8 Sonnenmassen an. In der Sonnenumgebung gilt zwischen 0.5 und 0.8 Sonnemassen noch immer und anschließend .
Ein großer Unsicherheitsfaktor stellt den Autoren zufolge der Anteil von Doppelsternen dar. Zum Teil fallen solche durch eine abnorme Lage im sogenannten Farben-Helligkeits-Diagramm auf. Bedecken sich die beiden Komponenten immer wieder gegenseitig, weil man das Doppelsystem von der Kante sieht, zeigen sich periodische Helligkeitsschwankungen. Allerdings ist eine Hochrechnung von diesen wenigen Fällen auf die Gesamtzahl von Doppelsystemen sehr ungenau. Insgesamt setzen Giersz und Heggie den Anteil der Doppelsterne im Vergleich zur unserer Umgebung erstaunlich gering an. Unmittelbar nach Entstehung des Haufens betrug er demnach lediglich 2.2% und ist seitdem durch Dreier- und Viererstöße auf gar nur noch 0.8% gefallen. Für das Zentrum von 47 Tucanae finden die Autoren dennoch einen völlig gegensätzlichen Trend. Unter den innersten 1000 Sternen ist seit Entstehung des Haufens ein geradezu dramatischer Anstieg des Doppelsternanteils von etwa 2% auf circa 14% zu verzeichnen, vor allem aufgrund der zunehmenden Konzentration massereicher Objekte zum Zentrum hin. Insbesondere enge Doppelsysteme können von anderen Sternen aus gesehen oft als massereiche Einzelobjekte betrachtet werden und unterliegen so in besonderem Maße der Massensedimentation.
Fortschreitende Sternentwicklung spielt bei einem so alten Objekt wie 47 Tucanae - die Autoren geben sein Alter mit 12 Milliarden Jahren an - erwartungsgemäß eine sehr wichtige Rolle. Der Haufen hat Giersz und Heggie zufolge bereits fast die Hälfte seiner Ursprungsmasse von etwa 1.6 Millionen Sonnenmassen eingebüßt - nur etwa 900000 Sonnenmassen sind heute noch vorhanden. Immerhin ein Drittel davon liegt bereits in Weißen Zwergen vor. Angesichts der von Anfang an geringen Zahl sehr massereicher Sterne sind hingegen deren Überreste wie Neutronensterne oder gar Schwarze Löcher selten. Die Autoren erwarten nur 300 Sonnenmassen in Form von Neutronensternen und lediglich 1-2 Dutzend Schwarze Löcher.
Wie schon anhand der einfachen Simulationsbeispiele in diesem Kapitel demonstriert, tendiert die Zentralregion eines Haufens dazu, zumindest vorübergehend im Laufe der Zeit sich zu verdichten. Der im Laufe der Sternentwicklung auftretende Massenverlust steht dem jedoch entgegen. Den Autoren gemäß hat der Radius, welcher die Hälfte der Masse von 47 Tucanae einschließt, sich seit dessen Entstehung von 1.9 auf 5.0 Parsec ausgedehnt. Mittlerweile wird der Haufen von massearmen Sternen dominiert, so dass in Zukunft Massenverlust keine bedeutende Rolle mehr spielen wird. Giersz und Heggie erwarten daher, dass sich 47 Tucanae in den nächsten 20 Milliarden Jahren wieder verdichten wird. Ist eine genügend hohe Dichte im Zentrum erreicht, können dort häufiger neue Doppelsterne entstehen und diese den Mechanismus der Beschleunigung eines nahe vorüberziehenden dritten Sterns wieder verstärken. Die Kontraktion kommt dadurch erneut zum Stillstand.
Simulationen mit und ohne primordiale Doppelsterne deuten an, dass diese während des Stadiums heftigen Massenverlusts noch keinen starken Einfluss auf die dynamische Entwicklung eines Kugelsternhaufens haben. Lässt der Massenverlust nach, verzögern die Doppelsysteme die nun einsetzende Verdichtung aber erheblich.
Einzelnachweise
- ↑ Röser H.-J., Tscharnuter W., Abriss der Astronomie 6.Auflage, Wiley-VCH, Berlin, S.970-971, 2012
- ↑ Salpeter E.E., The Luminosity Function and Stellar Evolution, in: Astrophysical Journal Band 121, S.161ff, 1955
- ↑ Kroupa P., On the Variation of the Initial Mass Function, in: Monthly Notices of the Royal Astronomical Society Band 322, S.231 ff, 2001
- ↑ 4,0 4,1 4,2 Aarseth S.J., Henon M, Wielen R., A Comparison of Numerical Methods for the Study of Star Cluster Dynamics, in: Astronomy and Astrophyscia Band 37, S.183 ff, 1974
- ↑ Röser H.-J., Tscharnuter W., Abriss der Astronomie 6.Auflage, Wiley-VCH, Berlin, S.627, 2012
- ↑ 6,0 6,1 Mardling R.A., The Role of Chaos in the Circularization of Tidal Capture Binaries. I - the Chaos Boundary, in: the Astrophysical Journal Band 450, S.722 ff, 1995 und Mardling R.A., The Role of Chaos in the Circularization of Tidal Capture Binaries. II - Long Term Evolution in: the Astrophysical Journal Band 450, S.732 ff, 1995
- ↑ Mardling R.A., Aarseth S.J., Tidal Interactions in Star Cluster Simulatios, in: Monthly Notices of the Royal Astronomical Society Band 321, S.398 ff, 2001
- ↑ 8,0 8,1 8,2 Mardling R.A., Stability in the General Three Body Problem, in: Astronomical Society of the Pacific Conference Series Band 229, S.101 ff, 2001
- ↑ Heggie D.C., Trenti M., Hut P., Star clusters with primordial binaries - I. Dynamic evolution of isolated models, in: Monthly Notices of the Royal Astronomical Society Band 368, S.677 ff, 2006
- ↑ Wisdom J., Holman M., Symplectic maps for the N-body problem, in: The Astronomical Journal Band 102, Nr.4, S.1528 ff, 1991
- ↑ Giersz M., Heggie D.C., Monte Carlo simulations of star clusters - VII. The globular cluster 47 Tuc, in: Monthly Notices of the Royal Astronomical Society Band 410, S.2698 ff, 2011





















![{\displaystyle T_{R}[a]=1.24\cdot 10^{6}{\frac {N}{\ln(N/2)}}{\sqrt {\frac {(R[pc])^{3}}{M[M_{S}]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c53e48d8a2b2db615da601bbd7e452eeb9f09bc3)




































































![{\displaystyle 1/[1-(r_{1}/R)]^{2}\approx 1+2r_{1}/R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59460cacb3d29593b9981e75f60c52aa889371e4)
![{\displaystyle 1/[1+(r_{1}/R)]^{2}\approx 1-2r_{1}/R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a16a9fd7f1ad93da98e60e277f8e93a4f02cfb03)








































