Einführung in die Systemtheorie/ Dynamische Systeme

Methoden der Systemtheorie

Schwerpunkt der Systemtheorie ist die Behandlung der verschiedenen dynamischen Systeme, deren Signale, die verschiedenen mathematischen Beschreibungen als Systemmodelle und die Systemberechnung. Folgende detaillierte Aufgabenbereiche und Systemdefinitionen sind damit verbunden:

• Definition dynamischer Systeme als Modell,
• Definition von Ein- und Mehrgrößensystemen,
• Identifikation der Systemstruktur,
• Verhalten linearer und nichtlinearer Systeme,
• Zeitverhalten: Systeme mit Zeitinvarianz und Zeitvarianz,
• Arten der mathematischen Beschreibung des Systemverhaltens:
  • Gewöhnliche Differenzialgleichung im Zeitbereich f(t)
  • Übertragungsfunktion im komplexen Frequenzbereich F(s)
  • Systemdarstellung im Zustandsraum f(t)
  • Zeitdiskrete Systembeschreibung und Systemberechnung f(k*Δt)
• Modellbildung eines Systems,
• Definition geeigneter Testsignale,
• Allgemeine Definition der Systemstabilität

Zum wirklichen Verständnis des Zeitverhaltens der dynamischen Systeme sind die Kenntnisse der gängigen mathematischen Berechnungsmethoden erforderlich. Dazu gehören die Kenntnisse der Entstehung und Lösung der gewöhnlichen Differenzialgleichung, die Anwendung der Laplace-Transformation, die Systembeschreibung mit der Übertragungsfunktion, für fachlich Fortgeschrittene die Systembehandlung im Zustandsraum und nicht zuletzt die numerische Berechnung dynamischer Systeme mit der diskreten Zeit Δt.

Totzeitbehaftete und nichtlineare dynamische Systeme und deren zugehörige Signale lassen sich zu einem vernünftigen Aufwand nur numerisch berechnen, alle anderen genannten mathematischen Beschreibungen sind nur bedingt brauchbar. Ist einer Übertragungsfunktion G(s) die transzendente Funktion des Totzeitgliedes $e^{-s\cdot T_{t}}$ multiplikativ angehängt, dann kann das Gesamtsystem nicht mehr algebraisch behandelt werden. [transzendent (Mathematik): über das algebraische hinausgehend].

Dieses vorliegende Kapitel "Dynamische Systeme" zeigt mit seinen Unterkapiteln vereinfacht den Einstieg in die mathematischen Beschreibungen, um den vorgezogenen Begriff "Dynamisches System" verstehen zu können.

Definition dynamisches System

Ein dynamisches System ist eine abgegrenzte zeitabhängige Funktionseinheit, die durch ihre Signaleingänge und Signalausgänge in einer Wechselwirkung mit der Umwelt steht. Das System kann beispielsweise ein mechanisches Gebilde, ein elektrisches Netzwerk aber auch ein biologischer Vorgang oder ein Bestandteil der Volkswirtschaft sein. Es hat mindestens einen Signaleingang und einen Signalausgang.

Dynamische Systeme werden mit Hilfe mathematischer Werkzeuge als Modelle eines realen Übertragungssystems beschrieben. Damit lässt sich für gegebene Eingangssignale der Verlauf der Ausgangssignale von einem bestimmten Zeitpunkt t = 0 = t₍₀₎ an für t > t₍₀₎ bestimmen. Ebenso eignen sich die Modelle zur Systemanalyse.

Systeme lassen sich in nichttechnische, natürliche oder künstliche - von Menschenhand geschaffene Einrichtungen - einteilen. Dennoch zeigen diese unterschiedlichen Systeme bei ähnlichen Strukturen als Modelle prinzipiell ähnliche mathematische Eigenschaften.

Ein technisches dynamisches System enthält einen oder mehrere Energiespeicher, die konzentriert oder räumlich verteilt angeordnet sind. Häufig werden bei Systemberechnungen zur Vereinfachung konzentrierte Energiespeicher angenommen. Systembeispiele: Feder-Masse-Dämpfungssystem, Elektrischer Schwingkreis.

Dynamische Systeme mit konzentrierten Systemspeichern enthalten Variablen als Funktion der Zeit. Dynamische Systeme mit räumlicher Verteilung der Systemspeicher enthalten Variablen als Funktionen der Zeit und des Ortes.

Das Ausgangs- Eingangsverhalten dieser Systeme kann linear, kontinuierlich nichtlinear, diskontinuierlich nichtlinear, zeitinvariant, zeitvariant und totzeitbehaftet sein. Dies gilt für Eingrößen- und Mehrgrößensysteme.

Ferner können die internen Energiespeicher Anfangswerte enthalten, wenn das Signalverhalten eines Systems zu einem bestimmten Zeitpunkt $t_{0}\,$ innerhalb eines Einschwingvorgangs für $t>0\,$ betrachtete werden sollen.

Statische lineare oder nichtlineare Systeme haben keine Energiespeicher und damit kein Zeitverhalten. Das Ausgangs- Eingangsverhalten wird durch algebraische oder transzendente (Trigonometrische oder exponentielle) Funktionen oder Wertetabellen beschrieben.

Viele technische dynamische Systeme enthalten Komponenten von mechanischen, elektrischen, elektronischen, hydraulischen und fluidischen (Fluidik = Elemente mit pneumatischer bzw. hydraulischer Hilfsenergie) Elementen. Bei gleicher Systemstruktur gelten die gleichen mathematischen Systembeschreibungen.

• Systeme mit konzentrierten und verteilten Energiespeichern

Ein technisches dynamisches System enthält einen oder mehrere Energiespeicher, die konzentriert oder räumlich verteilt angeordnet sind. Häufig werden bei Systemberechnungen zur Vereinfachung konzentrierte Energiespeicher angenommen.

Das zeitliche Verhalten des dynamischen Systems ist durch die inneren Systemgrößen bestimmt, die als Energiespeicher vorhanden sind und sich nicht sprunghaft ändern können. Sie bedeuten zum Beispiel "Spannung an einem Kondensator", "Strom in einer Induktivität", bei einem "Feder-Masse-Dämpfungssystem die potentiellen und kinetischen Energieanteile". Diese dynamischen Systemteile entsprechen den konzentrierten Energiespeichern.

Dynamische Systeme mit konzentrierten Systemspeichern enthalten Variablen als Funktion der Zeit.

Dynamische Systeme mit räumlicher Verteilung der Systemspeicher enthalten verteilte Systemparameter. Bei diesen Systemen sind die Variablen nicht nur Funktionen der Zeit sondern auch vom Ort. (Beschreibung durch partielle Differenzialgleichungen oder Näherungsmodelle)

Beispiele für kontinuierliche Systeme mit räumlich verteilten Energiespeichern stellen elektrische Leitungen im Rahmen der Leitungstheorie dar oder ein anderes Beispiel der Thermodynamik ist die räumliche oder flächenmäßige Wärmeenergie-Ausbreitung als Folge eines Energiesprunges in einem homogenen Medium (Metall, Flüssigkeit, Stein usw.).

• System mit Anfangswerten

Technische dynamische Systeme besitzen Speicher (Gedächtnis) der Materie, der Energie oder der Information. Die Gedächtniswirkung bezieht sich auf einen transienten Einschwingvorgang des Systems als Folge einer vorangegangenen Eingangserregung. Zu einem festgelegten beliebigen Zeitpunkt t = t₀ innerhalb des Einschwingvorgangs hat das System, das mehrere Energiespeicher enthalten kann, einen oder mehrere sogenannte Anfangswerte in den Speichern.

Signalflussplan zur Lösung einer DGL mit Anfangswerten in der expliziten Darstellung

Die Anfangswerte y₀₁...y_0n sind die inneren Systemgrößen eines dynamischen Systems während eines Einschwingvorgangs zu einem beliebigen Zeitpunkt t₀, zu dem das System betrachtet werden soll. Die Lösung einer systembeschreibenden Differenzialgleichung je nach Anzahl der Differenziale der Systemordnung beruht immer auf Anwendung von Integrationsfunktionen. Ein einzelner Anfangswert ist der Ausgangswert jeder der möglichen Integratoren, die zur Lösung der Differenzialgleichung zum Zeitpunkt t₀ notwendig sind.

Im Zustandsraum betrachtet, sind die Anfangswerte die Zustandsvariablen x₁...x_n eines dynamischen Systems zum Zeitpunkt t₀ in dem Signalflussplan der "Regelungsnormalform" dargestellt. Dabei entsprechen die jeweiligen Ausgänge der Integratoren zum Zeitpunkt t₀ den Zustandsvariablen und sind gleichzeitig die Anfangswerte.

Die bis in die 1960-er Jahre bevorzugte Lösung einer systembeschreibenden Differenzialgleichung durch einen Analogrechner ähnelt sehr stark der Regelungsnormalform des Zustandsraumes. Die Ausgangswerte der Integratoren zum beliebig wählbaren Zeitpunkt t₀ während des Einschwingvorgangs sind die Anfangswerte. Der Signalflussplan als mathematisches Modell eines Analogrechners ist heute in gleicher Weise gültig. Die Berechnung des Signalflussplans wird numerisch durchgeführt und bezieht sich auf die explizite (deutlich, eindeutig) Form der Differenzialgleichung, bei der die höchste Ableitung der Ausgangsgröße y(t) von der Gleichung freigestellt wird.

Die Integratoren des Modells starten mit dem Rechenprogramm bei der Eingangserregung z.B. u(t) = 0 von den eingestellten Anfangswerten. Siehe Signalflussplan an der Summenstelle für die höchste Ableitung ${\ddot {y}}(t)\,$. Die Lösung der Differenzialgleichung für y(t) wird so erzwungen.

Befindet sich das System nach genügend langer Zeit im Ruhezustand - d. h. der Einschwingvorgang ist abgeschlossen und das System-Eingangssignal hat den Wert Null - dann sind auch die Anfangswerte zu einem wählbaren Zeitpunkt t₀ gleich Null.

Hat das System eine Eingangserregung u(t) > 0, und der Einschwingvorgang ist nach genügend langer Zeit abgeschlossen, dann nimmt die Ausgangsgröße y(t) = x1(t) entsprechend der Proportionalverstärkung K den Wert der Eingangsgröße u(t) * K an. Zwingend notwendig ist dazu, dass die Variable x2(t) laut Signalflussplan den Wert Null annimmt, anderenfalls könnte sich kein statischer Wert für y(t) ergeben.

• Eingangserregung und Anfangswerte

In der Systemtheorie ist es üblich, den Beginn des Beobachtungszeitraumes eines dynamischen Vorganges formal bei t = 0 festzulegen, daher sind Testsignale am Eingang des Systems für den Zeitraum t < 0 gleich Null. Zu dem bestimmten Zeitpunkt t₀ , ab dem man das Verhalten des dynamischen Systems betrachten möchte, können die Energiespeicher des Systems Anfangswerte enthalten. Erhält das System zu diesem definierten Zeitpunkt t₀ eine Erregung, überlagern sich die Anfangswerte und die Wirkung der Eingangserregung für den Zeitraum $t>0$.

Ist die Eingangserregung zum Zeitpunkt t₀ gleich Null, ist das System mit Anfangswerten sich selbst überlassen und die Ausgangsgröße strebt zeitlich - ein stabiles System vorausgesetzt - einen Wert gegen Null bzw. die Ruhelage an. Handelt es sich um ein instabiles System (z.B. um ein System mit Rückkopplung), wird je nach Systemordnung zwischen monotoner und oszillatorischer Instabilität unterschieden. Dabei strebt die System-Ausgangsgröße zeitlich einen Maximalwert an. (Siehe Kapitel "Systemtheorie/ Übertragungsfunktion")

Für die Analyse und Ermittlung des Eingangs- Ausgangsverhalten von Systemen der regelungstechnischen Anlagen ist häufig das Systemverhalten ohne Anfangswerte von Interesse. Die Systemspeicher befinden sich bei t₀ im Ruhezustand und haben den Wert Null.

• Mathematisches Modell

Das dynamische System ist meist ein mathematisches Modell eines realen Übertragungssystems, welches mit Hilfe mathematischer Werkzeuge für gegebene Eingangssignale den Verlauf der Ausgangssignale von einem bestimmten Zeitpunkt t₍₀₎ = 0 an für t > t₍₀₎ bestimmt. Die häufigsten mathematischen Systembeschreibungen sind die Differenzialgleichung, die Übertragungsfunktion, der Frequenzgang und die zeitdiskrete Differenzengleichung. Enthalten die Systeme eine Totzeit (Transportzeit, Getriebespiele), Begrenzungseffekte oder andere Nichtlinearitäten kommt für die Systemberechnung praktisch nur die zeitdiskrete Differenzengleichung in Verbindung mit logischen Funktionen als Systembeschreibung infrage.

Ausnahmsweise werden auch physikalische materielle Modelle verwendet. Beispiele: Hydraulischer Strömungskanal im verkleinerten Maßstab, Regelkreisnachbildung mit einem Analogrechner.

Alle diese Systeme können sich linear, kontinuierlich nichtlinear, diskontinuierlich nichtlinear, zeitinvariant, zeitvariant und totzeitbehaftet als Eingrößen- und Mehrgrößensystem verhalten.

• Statisches System

Im Gegensatz zu den dynamischen Systemen hat ein statisches System im Sinne der Systemtheorie verschwindend kleine Energiespeicher und damit angenähert kein Zeitverhalten, sondern wird durch das Eingangs-Ausgangsverhalten des Systems definiert. Dieses Verhalten kann proportional, kontinuierlich linear, kontinuierlich nichtlinear oder diskontinuierlich (gebrochene Funktion) auftreten und wird – soweit möglich – durch eine mathematische Modellbeschreibung oder durch Wertetabellen angenähert beschrieben.

• System mit verzögerndem und voreilendem Ausgangsverhalten

Allgemein reagieren dynamische Systeme ohne Hilfsenergie bzw. ohne Verstärker, die aus mehreren Systemteilen bestehen können, signaltechnisch je nach System-Übertragungsverhalten mit einem meist verzögertem Signal des Systemausgangs. Enthält das System einen "Energieverstärker", kann statt einer verzögernden Wirkung eine vorauseilende Signalwirkung erreicht werden. Beispiele dafür sind die in der Regelungstechnik eingesetzten PD- und PID-Regler, aber auch gewollte Frequenzgang-Korrekturen des Systemverhaltens.

Einführung der mathematischen Systembeschreibung

Übersicht der mathematischen Systembeschreibung

Methoden der Beschreibung dynamischer Systeme

Ein dynamisches System hat ein Zeitverhalten und soll als Vereinfachung als ein System mit konzentrierten Energiespeichern beschrieben werden. Sind die physikalischen Komponenten eines beispielsweise schwingfähigen Systems - wie Feder-Masse-Dämpfungssystem - oder elektrisch - Kapazität-Induktivität-Widerstandssystem bekannt, können diese Systeme mit einer gewöhnlichen Differenzialgleichungen mit konstanten Koeffizienten beschrieben werden.

Da dieses genannte System zwei Energiespeicher (z.B. Feder und Masse) enthält, wird es durch eine gewöhnliche Differenzialgleichung zweiter Ordnung beschrieben.

Je nach vorhandenen Informationen und Systemverhalten eines dynamischen Systems existieren noch verschiedene andere mathematische Systembeschreibungen, die sich zur Systemanalyse, Systemidentifikation und Systemberechnung besser eignen.

Zum Verständnis der verschiedenen Arten der Systeme und des Systemverhaltens sind mathematische Beschreibungen von Teilsystemen, die in verschiedensten Strukturen auftreten können, erforderlich. Dazu gehört die Kenntnis der wichtigsten Begriffe der Systembeschreibung, die gewöhnliche Differenzialgleichung und Laplace-Übertragungsfunktion, die aus der Differenzialgleichung mittels der Laplace-Transformation bestimmt werden kann. Beide Methoden setzen lineare dynamische Systeme voraus. Weitere Systembeschreibungen wie die Differenzengleichungen und die Systembeschreibungen im Zustandsraum werden aus den Differenzialgleichungen abgeleitet.

Obwohl die Übertragungsfunktion G(s) eine Systembeschreibung linearer Systeme im komplexen Frequenzbereich s = δ + jω darstellt, kennzeichnet sie an Hand der symbolischen Darstellung einfacher algebraischer Gleichungen das charakteristische Systemverhalten im Zeitbereich. Es existieren nur 6 verschiedene Formen einfacher oder mehrfacher Kombinationen davon.

Totzeitbehaftete nichtlineare dynamische Übertragungssysteme lassen sich meist in statische nichtlineare Systeme und dynamische lineare Systeme aufteilen und beschreiben. Das Zeitverhalten dieser Systeme kann nur numerisch errechnet werden, weil Nichtlinearitäten Unikate sind, die mit logischen Programmbefehlen oder Datentabellen beschrieben werden können.

Nachfolgend findet eine Kurzdarstellung dieser Systembeschreibungen statt.

Einführung der Systembeschreibung mit Differenzialgleichungen

Die wichtigste mathematische Systembeschreibung ist die Differenzialgleichung, welche die speziellen physikalischen Grundgesetze des zeitlichen Verhaltens eines bestimmten dynamischen Systems beschreibt. Mit den Differenzialgleichungen lassen sich viele dynamische Systeme aus der Technik, Natur und Gesellschaft darstellen. Viele scheinbar sehr verschiedene physikalische Probleme lassen sich mit der Differenzialgleichung jedoch formal identisch berechnen.

Eine systembeschreibende Differenzialgleichung ist durch die Differentiale der Energiespeicher und der Ein-Ausgangssignale bestimmt. Die Differenzialgleichung eines dynamischen Systems beschreibt den Zusammenhang zu jedem Zeitpunkt zwischen der Ausgangsgröße y(t) und der Eingangsgröße u(t). Die Ordnung der Differentialgleichung ist durch die Ordnung der höchsten vorkommenden Ableitung gegeben.

Andere bekannte Systembeschreibungen der dynamischen Systeme lassen sich von den Differenzialgleichungen entwickeln, wie die Übertragungsfunktion mit dem komplexen Frequenzbereich f(s), der Frequenzgang f(jω), die Zustandsraumdarstellung und die für die numerische Berechnung benötigten Differenzengleichungen.

Mathematische Modelle der dynamischen Systeme werden je nach Kenntnis und Verfügbarkeit der Systemparameter durch verschiedene mathematische Beschreibungsmethoden gekennzeichnet, bzw. angenähert.

Systemtrennung in statisches nichtlineares System und lineares dynamisches System.

Nichtlineare dynamische Systeme können zur einfacheren Berechnung auch durch Modelle in Kombinationen von nichtlinearen Systemen ohne Zeitverhalten und linearen dynamischen Systemen aufgeteilt werden, z.B. nach dem Hammerstein-Modell. Nichtlineare statische Modelle sind meist Unikate.

Die Berechnung dynamischer Systeme dient der Kenntnis des Ausgangs-Eingangsverhaltens und der Systemanalyse. Je nach Art des dynamischen Systems eignen sich verschiedene mathematische Beschreibungs- und Berechnungsverfahren:

Gewöhnliche Differenzialgleichung höherer Ordnung mit konstanten Koeffizienten

Eine Differentialgleichung ist eine Gleichung, die eine oder mehrere Ableitungen einer unbekannten Funktion enthält. Die Bezeichnung "gewöhnlich" bezieht sich darauf, dass die gesuchte Funktion nur von einer Variablen abhängt. Es wird nur nach einer Variablen abgeleitet. Eine lineare gewöhnliche Differenzialgleichung enthält die gesuchte Funktion und deren Ableitungen nur in der ersten Potenz. Die gesuchte Funktion darf auch nicht in Argumenten von Winkelfunktionen, Logarithmen usw. erscheinen, anderenfalls wird die Differenzialgleichung nichtlinear. Nichtlineare Differenzialgleichungen mit den verschiedenen Arten der Nichtlinearität sind nur in sehr seltenen Ausnahmefällen analytisch lösbar. Solche dynamischen Systeme können mittels der numerischen zeitdiskreten Methoden beschrieben und berechnet werden.

Die häufigsten mathematischen Systembeschreibungen linearer Systeme sind gewöhnliche Differenzialgleichungen mit konstanten Koeffizienten. Zur Aufstellung der Differenzialgleichungen höherer Ordnung werden Bilanzgleichungen der Energie / Materie-Speicher benötigt. Systeme mit konzentrierten Speichern erfordern für jede Speicherfunktion eine Differenzialgleichung 1. Ordnung. Diese Differenzialgleichungen mit den Anfangsbedingungen = Null können am einfachsten über die Laplace-Transformation gelöst werden.

Bei dynamischen Systemen in Form ausgeführter technischer Anlagen stehen Differentialgleichungen selten zur Verfügung. Das Systemverhalten muss erst noch analysiert und dann formuliert werden.

Beispiel einer gewöhnliche Differenzialgleichung n-ter Ordnung mit konstanten Koeffizienten a und b für ein System mit dem Ausgangssignal y(t) und Eingangssignal u(t):

$a_{n}y^{(n)}+\ldots +a_{2}{\ddot {y}}+a_{1}{\dot {y}}+a_{0}y=b_{m}u^{(m)}+\ldots +b_{2}{\ddot {u}}+b_{1}{\dot {u}}+b_{0}u\,$

Differenzialgleichung höherer Ordnung mit variablen Koeffizienten

• Sind diese Koeffizienten oder nur ein Koeffizient dieser Differenzialgleichung variabel, dann ändert sich das Zeitverhalten des dynamischen Systems, d.h. eine Sprungantwort des Systems für einen gegebenen Eingangssprung nimmt einen anderen zeitlichen Verlauf. Dieses Verhalten wird leicht verständlich, wenn man die Laplace-transformierte Differenzialgleichung als Übertragungsfunktion betrachtet.
• Sind die Koeffizienten zeitabhängig, führt dieses zu zeitvariantem Systemverhalten, d.h. das Zeitverhalten des Systems ist zu unterschiedlichen Zeitpunkten für t > t₀ unterschiedlich. Systembeispiel: Wenn bei einer beschleunigten Rakete die Masse des Treibstoffs sich ändert.

Partielle Differenzialgleichung

Bei partiellen Differenzialgleichungen hängt die gesuchte Funktion von mehreren Variablen ab. Es wird nach mehreren Variablen abgeleitet. Die Anwendung dieser Gleichung erfolgt z.B. bei dynamischen Systemen mit Zeit- und Ortskoordinaten.

Systembeispiel: Signalübertragung bei langen elektrischen Leitungen oder Wärmefluss in homogenen Medien.

Beispiel der Entstehung einer Differenzialgleichung mit elektrischen Bauelementen

Schaltplan eines elektrischen Schwingkreises

L = Induktivität, C = Kondensator, R = Widerstand, UC = Spannung am Kondensator = Ausgangsgröße, UE = Eingangsspannung $L\cdot C\cdot {\ddot {U}}_{C}(t)+R\cdot C\cdot {\dot {U}}_{C}(t)+U_{C}(t)=U_{E}(t)\,$ Es können Zeitkonstanten wie T1 = R * C und T2² = L * C eingeführt werden mit y(t) = Ausgangsgröße, u(t) = Eingangsgröße. $T_{2}^{2}\cdot {\ddot {y}}(t)+T_{1}\cdot {\dot {y}}(t)+y(t)=u(t)\,$ oder in allgemeiner Koeffizienten-Darstellung: $\quad a_{2}=1;\quad a_{1}={\frac {R}{L}};\quad a_{0}={\frac {1}{L\cdot C}};\quad b_{0}={\frac {1}{L\cdot C}}\,$ ${\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)\,$

Einführung der konventionellen Lösung einer gewöhnlichen Differenzialgleichung

Die Lösung einer Differenzialgleichung (DGL) erfolgt immer durch Integration und ist eine Funktion, nicht ein Wert. Natürlich kann auch ein bestimmter Wert der Ausgangsgröße für eine bestimmte Zeit errechnet werden.

Die Lösung der Differenzialgleichung ist die Ausgangsgröße y(t) in Abhängigkeit der Art und Größe des gegebenen Eingangssignals u(t). Eingangssignale sind häufig Testsignale wie die Sprung- und Impulsfunktion, die charakteristische Signalantworten des Systems hervorrufen, die der Systemdiagnose dienen können.

Die gewöhnliche Differenzialgleichung (DGL) beschreibt ein lineares Übertragungssystem mit n Energiespeichern durch n Ableitungen der Systemausgangsgröße y(t) und m Ableitungen der Eingangsgröße u(t) des Systems. Die Lösung einer DGL erfolgt durch Integration. Jede unbestimmte Integration ergibt Integrationskonstanten C_n, deren Anzahl durch die Ordnung n der DGL festgelegt ist.

Für ein gegebenes Eingangssignal an dem linearen dynamischen System mit Anfangswerten ergibt sich als Lösung der systembeschreibenden gewöhnlichen DGL eine Addition aus zwei Lösungsanteilen, der homogenen und partikulären Lösung, die einen Funktionsverlauf f(t) der Ausgangsgröße des Systems darstellen. Die konventionelle Lösung einer inhomogenen DGL besteht aus der allgemeinen Lösung der homogenen DGL mit der Ausgangsgröße y_H(t) mit der Eingangsgröße u(t) = 0 sowie einer speziellen partikulären Lösung der inhomogenen DGL y_P(t) mit u(t) ≠ 0.

Inhomogene DGL = DGL mit u(t) ≠ 0)

• Bei der homogenen Lösung der DGL liegen Anfangswerte vor. Die Systemeingangsgröße u(t) ist dabei gleich Null. Das System ist sich selbst überlassen und strebt einen stabilen Ruhezustand an, Systemstabilität vorausgesetzt.
• Bei der partikulären Lösung der DGL sind die Anfangswerte gleich Null und die Systemeingangsgröße u(t) ≠ Null.
• Die Summe der beiden Ausgangs-Teilgrößen y(t) = y_H(t) + y_P(t) ergibt die Gesamtlösung.

Differenzialgleichung mit Anfangswerten

Die Anfangsbedingungen beschreiben einen speziellen Zustand des Übertragungssystems. Die homogene (charakteristische) DGL beschreibt das Verhalten ohne Eingangsgröße (für u(t) = 0), das sogenannte Eigenverhalten, d. h. das System bleibt ausgehend von den Anfangswerten sich selbst überlassen.

Sind alle Anfangswerte der homogenen DGL gleich Null, ist die Lösung der DGL für y_H(t) auch gleich Null. Mit dem Lösungsansatz $y=e^{{\lambda }\cdot t}\,$ ergibt sich ein universelles Lösungsverfahren für die homogene Lösung der DGL-en beliebiger Ordnungen mit konstanten Koeffizienten.

$y_{H}(t)=C_{1}\cdot e^{{\lambda }_{1}\cdot t}+C_{2}\cdot e^{{\lambda }_{2}\cdot t}+C_{3}\cdot e^{{\lambda }_{3}\cdot t}+\cdots$

Die partikuläre Lösung der DGL eines Systems höherer Ordnung (> 2. Ordnung) über das Faltungsintegral gestaltet sich schwierig. Einfacher wird die Lösung über die Laplace-Transformation und noch einfacher und übersichtlicher mit Hilfe der numerischen Berechnung.

Definition Anfangswertproblem

(Anfangswertproblem = Differenzialgleichung mit ihren zugehörigen Anfangswerten)

Das eigentliche Anfangswertproblem besteht darin, mit den gegebenen Anfangswerten y₀ und y'₀ ... y⁽ⁿ⁾₀ und den Eigenwerten λ_n (Nullstellen) der DGL die Integrationskonstanten C_n zu berechnen. Die Anfangswerte werden in die Lösungsgleichung anstelle von y_H(t) eingesetzt. Dabei werden die Terme der DGL entsprechend der Ordnung differenziert und dann die Gleichungen für t = 0 berechnet. Damit ergeben sich entsprechend der Ordnung n der DGL n Gleichungen, aus denen die Integrationskonstanten errechnet werden können.

Die Berechnung der Integrationskonstanten ist leider sehr umständlich, gehört aber zur klassischen Lösung der DGL.

Anwendung dynamisches System mit Anfangswerten

Der Zustand eines dynamischen Systems (z.B. Regelstrecke) ist durch den Energiegehalt der im System enthaltenen Energiespeicher bestimmt. Zu einem beliebigen Zeitpunkt t = t₀, der als Anfangszustand der Ausgangsgröße y(t) bezeichnet wird, folgt die Ausgangsgröße y(t) in Abhängigkeit des Anfangszustandes und des Eingangssignals u(t) für t>t₀ für beliebig lange Zeiten. Dazu wird die Vorgeschichte des Systems für t < 0 nicht benötigt.

Verzichtet man auf die Berechnung einer DGL mit Anfangswerten eines Übertragungssystems, kann mit Hilfe der Übertragungsfunktion G(s) und Laplace-Transformationstabellen die Lösung der Differenzialgleichung für gegebene Eingangssignale im Zeitbereich bestimmt werden.

Ist die Übertragungsfunktion G(s) als Laplace-transformierte Differenzialgleichung gegeben, so ist die Berechnung des System-Ausgangssignals y(t) für ein gegebenes Eingangssignal Y(s) bei Anwendung der inversen Laplace-Transformation immer eine partikuläre Lösung. Die partikuläre Lösung der Differenzialgleichung ist in der Regelungstechnik meist von hauptsächlichem Interesse.

In der Regelungstechnik werden häufig Übertragungssysteme durch Aufzeichnung der Sprungantwort analysiert. Dabei wird meistens vorausgesetzt, dass sich das System in Ruhe befindet. Es gibt aber Anwendungen, bei denen die Speicher "Anfangswerte" haben oder das System bei Anfangswerten getestet werden sollen, um spezielle Aussagen zu treffen.

Numerische Lösung der Differenzialgleichung mit Anfangswerten

Für viele dynamische Systeme sind nicht immer die physikalischen Einzelkomponenten bekannt und damit kann auch keine Differenzialgleichung aufgestellt werden. Außerdem ist die Lösung einer gewöhnlichen Differenzialgleichung höherer Ordnung schwierig.

Mit Hilfe von Testsignalen und Aufzeichnung der Systemreaktion kann ein dynamisches System identifiziert werden. Bei linearen Systemen wird vorzugsweise die Übertragungsfunktion G(s) als Funktion der komplexen Frequenz s benutzt. Die Zerlegung in Teilsysteme - Linearfaktoren - entspricht der kleinsten Systemeinheit G(s) der gewöhnlichen Differenzialgleichungen 1. Ordnung.

Die numerische Berechnung bezieht sich auf ein konstantes kleines Zeitintervall Δt, der diskreten Zeit. Für dieses Zeitintervall wird an Hand von Differenzengleichungen rekursiv (Rekursion = zurücklaufen) das Systemausgangssignal mit der Folge (k*Δt) neu berechnet und bildet damit einen fein gestuften Signalverlauf als Funktion der Zeit.

Es bestehen mehrere Methoden der Bildung von Differenzengleichungen. Die einfachste Methode ist das Verfahren nach dem "Euler-Streckenzugverfahren", das mit 4 verschiedenen Differenzengleichungen sämtliche lineare Übertragungssysteme approximieren (annähern) kann.

Bei der numerischen Berechnung eines Übertragungssystems mit Anfangswerten oder ohne Anfangswerte ergibt sich das Anfangswertproblem nicht. Die numerische Berechnung bezieht sich dabei auf den Signalflussplan der Regelungsnormalform des Zustandsraumes. Dies entspricht im Prinzip dem Signalflussplan des Analogrechners. Die numerische Integration bezieht sich dabei auf ein bestimmtes Integral. Die Integrationsgrenzen beginnen mit den jeweiligen Anfangswerten bei t₀ und enden mit der gewünschten Betrachtungsdauer der rekursiven Berechnungsfolgen k_MAX*Δt. Die Integratoren werden zu Beginn der Berechnung auf die gewünschten Anfangswerte gesetzt. Die System-Ausgangsgröße y(t) entspricht immer der Addition der homogenen und partikulären Lösung der DGL.

Sind keine Anfangswerte des Systems gegeben, so können die Systemteile numerisch durch Anwendung von Differenzengleichungen sehr einfach gelöst werden.

→ Siehe das ausführliche Kapitel "Einführung in die Systemtheorie/ Numerische Berechnung dynamischer Systeme".

→ Siehe das ausführliche Kapitel "Einführung in die Systemtheorie/ Gewöhnliche Differenzialgleichungen".

Einführung der Systembeschreibung mit der Übertragungsfunktion G(s)

Der Begriff Übertragungsfunktion hat verschiedene Bedeutungen und kennzeichnet allgemein die Abhängigkeit des Ausgangssignals Y eines Übertragungssystems G von dessen Eingangssignal U.

Neben dem Begriff Laplace-Übertragungsfunktion G(s) - in der Regelungstechnik vereinfacht "Übertragungsfunktion" genannt - existiert auch der Begriff der "Z-Übertragungsfunktion", die aus der Übertragungsfunktion G(s) entstanden ist. Während Differenzialgleichungen für kontinuierliche Signale mit der Laplace-Transformation gelöst werden können, hat die Z-Transformation für zeitdiskrete Signale bei abgetasteten Signalfolgen eine ähnliche Bedeutung. Die Anwendung der Z-Übertragungsfunktion bei abgetastete Signalfolgen ist nicht zwingend, es können auch zur numerischen Systemberechnung Differenzengleichungen des Systems verwendet werden. Die Z-Übertragungsfunktion ist nicht Gegenstand dieses Kapitels.

Die Übertragungsfunktion G(s) eines linearen dynamischen Systems g(t) entsteht z. B. aus der Laplace-Transformation einer systembeschreibenden gewöhnlichen Differenzialgleichung. Sie ist in der Regelungstechnik die häufigste Darstellungsform des Eingangs- und Ausgangsverhaltens von linearen Übertragungssystemen im komplexen Frequenzbereich.

Die Übertragungsfunktion G(s) ist eine abstrakte nicht messbare Größe und beschreibt das mathematische Verhalten eines linearen zeitinvarianten Systems im Frequenzbereich mit der komplexen Variable s. Sie wird nach der Zerlegung der Zähler- und Nennerpolynome durch Nullstellenbestimmung in Produktterme (Linearfaktoren) erfolgreich eingesetzt für Systemanalyse, Systemsynthese, Systemstabilität und erlaubt die algebraische Behandlung von beliebig geschalteten rückwirkungsfreien Teilsystemen.

Die Übertragungsfunktion G(s) beschreibt das Verhältnis der Ausgangsgröße Y(s) zu der Eingangsgröße U(s) im Bildbereich, ist unabhängig von seinen Signalen und gültig in einem linearen und zeitinvarianten System (d. h., das Systems zeigt zu jeder Zeit - bei gleicher Erregung - das gleiche Verhalten).

Die allgemeine Form der Übertragungsfunktion G(s) lautet in Polynomdarstellung:

$G(s)={\frac {Y(s)}{U(s)}}:={\frac {b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s+a_{0}}}:={\frac {\text{Zählerpolynom (s)}}{\text{Nennerpolynom (s)}}}$

Beispiel einer Übertragungsfunktion G(s) der 3. Ordnung mit den Koeffizienten a_i und b_i in Polynomdarstellung mit n > m

$G(s)={\frac {Y(s)}{U(s)}}:={\frac {b_{2}\cdot s^{2}+b_{1}\cdot s+b_{0}}{a_{3}\cdot s^{3}+a_{2}\cdot s^{2}+a_{1}\cdot s+a_{0}}}$

Definition der Systemgrößen:

• G(s) ist die Laplace-Transformierte von g(t). Die symbolische Schreibweise lautet:

$G(s)={\mathcal {L}}\{g(t)\}\quad {\text{oder als inverse Laplace-Transformation}}\quad g(t)={\mathcal {L}}^{-1}\{G(s)\}$

G(s) beschreibt das dynamische System mit einer Gleichung in Form einer gebrochen-rationalen Funktion unter der Voraussetzung, dass die internen Energiespeicher des dynamischen Systems gleich Null sind (d. h. verschwindende Anfangsbedingungen). Die Übertragungsfunktion kann über die Laplace-Transformation der systembeschreibenden gewöhnlichen Differenzialgleichung entstehen. Andere Entstehungsweisen sind die empirische Messung und Auswertung des Frequenzgangs $G(j\omega )$, die Systemanalyse mit Hilfe der Impuls- oder der Sprungantwort oder die Bildung des Impedanzverhältnisses des unbekannten linearen Systems.

• Y(s) ist das Systemausgangssignal,
• U(s) ist das Eingangssignal, welches als Testsignal häufig die Funktion eines Signalsprungs, eines Signalimpulses oder einer sinusförmigen Erregung hat.
• Die komplexe Frequenz $s=\delta +j\omega =Re(s)+j\cdot Im(s)$ ist eine unabhängige Variable des Laplace- oder Bildbereichs. Sie tritt mit einem ganzzahligen Exponenten als Potenz im Zähler und Nenner einer Übertragungsfunktion auf, ist aber nur ein Symbol für eine vollzogene Transformation einer Ableitung bestimmter Ordnung n oder eines Integrals der gewöhnlichen Differenzialgleichung. Die Variable s in verschiedenen Darstellungsarten der Übertragungsfunktion kann beliebig algebraisch behandelt werden, enthält aber keinen Zahlenwert.
• b_i = Koeffizienten des Zählers, a_i = Koeffizienten des Nenners.
• n und m bedeuten jeweils den Grad des Nennerpolynoms und des Zählerpolynoms (Ordnung des Systems). In der Produktdarstellung bedeutet n die Anzahl der Pole im Nenner, m die Anzahl der Nullstellen im Zähler. Sind alle Koeffizienten der Polynomdarstellung in der geordneten Reihenfolge vorhanden, positiv und die Systemordnung n > m, handelt es sich um ein asymptotisch stabiles Übertragungssystem.

Wird die Übertragungsfunktion der Polynomdarstellung in die Produktdarstellung gebracht, können sämtliche Systemeigenschaften wie die Kriterien der Stabilität, Pole, Nullstellen, Verstärkung und Zeitkonstanten aus der Übertragungsfunktion abgeleitet werden. Durch die Rücktransformation mittels der inversen Laplace-Transformation kann das zeitliche Verhalten eines Übertragungssystems als Funktion des Eingangssignals berechnet werden.

Entstehung der Übertragungsfunktion

Die Übertragungsfunktion G(s) beschreibt nach der Systemtheorie die mathematische Beziehung zwischen einem dynamischen System und den zugehörigen Ein- und Ausgangssignalen im sogenannten s-Bereich. Elektrische, mechanische, biologische und andere dynamische Systeme können durch die gleiche Form der Übertragungsfunktion beschrieben werden, wenn die Anzahl und die Struktur der Systemspeicher identisch sind.

Beispiel für eine Identifikation eines PT2-Schwingungsgliedes durch die Amplituden der 1. und 2. Halbwelle

Es bestehen mehrere Wege, die zu einer Übertragungsfunktion G(s) führen:

• Laplace-Transformation der systembeschreibenden gewöhnlichen Differenzialgleichung,
• aus dem Signalverhältnis Y(s) / U(s), wenn dieses bekannt ist.
• durch Messen des Frequenzgangs G(jω),
• Spannungsteiler aus einem rückwirkungsfreien Impedanzverhältnis, (Beispiel: RC-beschalteter Operationsverstärker),
• durch Systemidentifikation mittels Sprung- oder Impulsantwort

Die "klassische" Entstehungsweise der Übertragungsfunktion ergibt sich über die Laplace-Transformation der systembeschreibenden Differenzialgleichung mit konstanten Koeffizienten. Das Ergebnis ist eine Polynomgleichung mit der komplexen Frequenz s, die als Stellvertreter für jeden Differentialquotienten steht. Diese Transformation erfolgt nach dem Differentiationssatz der Laplace-Transformation. Der Grad, d.h. die Ordnung des Differentialquotienten entspricht dem Exponenten von s.

Enthält die Differenzialgleichung auch Ableitungen der Systemeingangsgröße, dann entsteht durch die Transformation eine gebrochene rationale Funktion G(s) als Quotient mit Polynomen im Nenner und Zähler. Sind keine Ableitungen der Eingangsgröße gegeben, existiert nach der Transformation nur ein Nennerpolynom der Übertragungsfunktion. Im Zähler der Übertragungsfunktion steht für diesen Fall die Verstärkung K, die auch die Größe 1 betragen kann.

Laplace-Transformation einer linearen gewöhnlichen Differenzialgleichung

Die Übertragungsfunktion entsteht durch die Laplace-Transformation, eine Integraltransformation, aller zeitabhängigen Terme der System-Differenzialgleichung und beschreibt das Übertragungsverhalten im sogenannten Bild- oder Frequenzbereich (s-Bereich) mit der der komplexen Variablen s.

Die Übertragungsfunktion eines Systems entsteht z.B. durch Austausch der zeitabhängigen Terme einer systembeschreibenden Differentialgleichung mit den Laplace-Transformierten. Voraussetzung ist, dass die Anfangsbedingung des Systems Null ist.

Je nach Grad der Ableitungen einer Funktion x(t) entstehen mit Hilfe des Laplace-Differentiationssatzes nach der Transformation folgende Laplace-Transformierte:

${\mathcal {L}}\left\{{\frac {}{}}x(t)\right\}=x(s)$

${\mathcal {L}}\left\{{\frac {d}{dt}}x(t)\right\}=s\cdot x(s)$

${\mathcal {L}}\left\{{\frac {d^{2}}{dt^{2}}}x(t)\right\}=s^{2}\cdot x(s)$

Der Grad der Ableitung im Zeitbereich und die zugehörige Transformierte im Bildbereich kann in dieser Weise beliebig fortgesetzt werden. Der Laplace-Operator s entspricht also der 1. Ableitung einer Funktion f(t), s² entspricht der 2. Ableitung einer Funktion f(t) und so weiter.

Für das Integral gilt die Laplace-Transformierte:

${\mathcal {L}}\left\{\int {x(t)dt}\right\}={\frac {1}{s}}\cdot x(s)$

Das dynamische Verhalten von linearen Übertragungssystemen (LZI-Systeme) wird durch gewöhnliche Differenzialgleichungen beschrieben. Der Wert der Ordnung n gibt die höchste Ableitung der Ausgangsgröße y(t) und damit allgemein die Anzahl der Energiespeicher des Übertragungssystems wieder.

Eine allgemein geordnete gewöhnliche Differenzialgleichung n-ter Ordnung lautet wie folgt:

(mit y(t) als Ausgangssignal und u(t) als Eingangssignal)

$a_{n}y^{(n)}+\ldots +a_{2}{\ddot {y}}+a_{1}{\dot {y}}+a_{0}y=b_{m}u^{(m)}+\ldots +b_{2}{\ddot {u}}+b_{1}{\dot {u}}+b_{0}u\,$

Falls die Koeffizienten $a_{i}$ und $b_{k}$ alle konstant sind, ist die Laplace-Transformation ausführbar. Allgemein gilt für die Signale u(t) und y(t) mit den zu Null gesetzten Anfangsbedingungen:

$y^{(i)}(0)=0\,$ für alle $0\leq i\leq n\,$

Damit lautet die Laplace-Transformierte der Übertragungsfunktion als Polynomgleichung:

$Y(s)(a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s+a_{0})=U(s)(b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0})$

Die Polynomgleichung kann so umgestellt werden, dass ein Verhältnis der Ausgangsgröße Y(s) zur Eingangsgröße U(s) gebildet werden kann. Der Rest der Terme der Polynomgleichung entspricht dem Übertragungssystem G(s) in Form einer gebrochen-rationalen Funktion, also einem Verhältnis aus Zähler und Nenner.

Die Übertragungsfunktion als eine rational gebrochene Funktion in Polynom-Darstellung lautet

$G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s+a_{0}}}$.

Für die Anwendung der Übertragungsfunktion zur Systemberechnung wird der Zustand der Energiespeicher des dynamischen Systems zum Zeitpunkt t = 0 als energiefrei angesehen. Damit werden die Anfangswerte des Systems zu Null.

Eine wesentliche nützliche Eigenschaft der Laplace-Übertragungsfunktion besteht darin, dass zwischen allen Komponenten ein algebraischer Zusammenhang besteht. Ein weiterer Vorteil besteht darin, dass mit Hilfe von Laplace-Transformationstabellen die Umwandlung vom s-Bereich in den Zeitbereich überführt werden kann und somit eine gewöhnliche Differenzialgleichung gelöst werden kann.

Definition Nullstellen und Pole

Ein lineares zeitinvariantes Übertragungssystem ohne Totzeit ist durch Pole, Nullstellen und Proportionalitätsfaktoren der Übertragungsfunktion vollständig bestimmt.

Die Ermittlung der Pole und Nullstellen der Polynome einer Übertragungsfunktion erlaubt die Umwandlung der Polynomdarstellung in eine Produktdarstellung. Die Übertragungsfunktion in der Produktdarstellung führt bei einem gegebenen Eingangssignal über die Laplace-Rücktransformation direkt zu einer Lösung im Zeitbereich. Die Produktdarstellung einer Übertragungsfunktion entspricht einer multiplikativ angeordneten Reihendarstellung von Teilsystemen (Elementarsystemen, Linearfaktoren), wobei ein Teilsystem nicht durch nachfolgende Teilsysteme belastet sein darf.

Zur Nullstellenbestimmung eines Polynoms mit Zahlenwerten werden die Polynome des Zählers und des Nenners der Übertragungsfunktion jeweils gleich Null gesetzt. Bei der Darstellung der Übertragungsfunktion als eine rational gebrochene Funktion werden die Nullstellen des Zählerpolynoms, die das Polynom zu Null machen, als Nullstellen $s_{n}$ bezeichnet. Die Nullstellen des Nennerpolynoms bezeichnet man als Pole $s_{p}$.

Polynome des 2. Grades können mit Hilfe der bekannten "pq-Gleichung" zur Lösung von gemischt-quadratischen Gleichungen gelöst werden. Es existieren noch weitere Verfahren zur Nullstellenbestimmung von Polynomen höheren Grades.

In dieser allgemeinen Darstellung ist noch nicht definiert, um welche Art von elementaren Produkten (= Linearfaktoren) es sich bei der Übertragungsfunktion handelt. Das Systemverhalten wird erst deutlich, wenn Zahlenwerte für die Nullstellen, Pole und Verstärkung $k$ vorliegen.

Ein Polynom hat so viele Nullstellen (bzw. Pole), wie es dem höchsten Grad der Ordnung entspricht. Je nach Größe und Anzahl der Koeffizienten der Polynome ergeben sich bei der Pol- Nullstellenbestimmung für die zu bestimmenden Werte der Pole und Nullstellen unterschiedliche mathematische Formen für $s_{n}$ und $s_{p}$, die Null, ± reell und ± konjugiert komplex sein können.

Die Werte von Polen und Nullstellen stabiler Elementarsysteme sind immer negativ. Positive Werte von Polen und Nullstellen führen zur monotonen oder oszillatorischen Instabilität des Gesamtsystems. Pole und Nullstellen haben die Maßeinheit einer Frequenz.

Die Pole bestimmen das Zeitverhalten des Systems, Nullstellen die Systemamplituden. Sind alle Realteile der Pole eines zeitinvarianten dynamischen Systems negativ und von Null verschieden, so ist das Übertragungsverhalten asymptotisch stabil. Bei einem Produktterm mit einem Pol, dessen Realteil und Imaginärteil Null ist, verhält sich das Gesamtsystem semistabil (integrierendes Verhalten).

Linearfaktoren

Sind die Nullstellen bzw. die Pole eines Polynoms bekannt, kann das Zähler- und Nennerpolynom in Produktterme (Linearfaktoren) zerlegt werden. Weil die Nullstellen aus zu Null gesetzten Polynomen berechnet werden, muss sichergestellt werden, dass keine Faktoren gekürzt worden sind. Es empfiehlt sich eine Prüfung vorzunehmen, ob die Pol- Nullstellendarstellung (= Produktdarstellung) durch Ausmultiplizieren auch mit dem Polynom identisch ist.

Eine Nullstelle des Zählerpolynoms s_n oder ein Pol des Nennerpolynoms s_p kann bei asymptotischer Stabilität des Teilsystems folgende drei Formen von Zahlenwerten einnehmen:

• {s_n; s_p} = 0, (Absolutglied $a_{0};b_{0}$ des Polynoms fehlt),
• {s_n; s_p} = $-\delta$ (reeller Wert der Pole und Nullstellen),
• {s_n; s_p} = $-\delta \pm j\omega$ (konjugiert komplexer Wert der Pole oder Nullstellen).

Bezeichnet man den Realteil einer Nullstelle oder eines Poles mit $\delta$ und den Imaginärteil mit $j\omega$, dann ergeben sich bei Übertragungsfunktionen in der Produktdarstellung bei reellen und konjugiert komplexen Nullstellen und Polen unterschiedliche Gleichungen, die durch die Größe der Zahlenwerte der Koeffizienten der Polynomdarstellung bestimmt werden. Die angegebenen drei Formen der Linearfaktoren können einfach und mehrfach auftreten.

In der linearen Regelungstechnik und Systemtheorie ist es eine willkommene Tatsache, dass praktisch alle vorkommenden regulären (stabilen) Übertragungsfunktionen bzw. Frequenzgänge von Regelkreisgliedern auf drei Grundformen geschrieben bzw. zurückgeführt werden können. Die Linearfaktoren haben eine völlig unterschiedliche Bedeutung, je nachdem ob sie im Zähler oder im Nenner einer Übertragungsfunktion stehen.

Stehen die Linearfaktoren im Zähler, haben sie eine differenzierende Wirkung, stehen sie im Nenner, haben sie eine verzögernde (speichernde) Wirkung:

Typ Linearfaktor (Zeitkonstanten-Darstellung)	Bedeutung im Zähler	Bedeutung im Nenner
$G_{1}(s)=T\cdot s$ Nullstelle $s_{n1}=0\ {\mathrel {\hat {=}}}\$ "Absolutglied fehlt"	Differenzierer, D-Glied	Integrator, I-Glied
$G_{2}(s)=T\cdot s+1$ Nullstelle $s_{n2}=-\delta \ {\mathrel {\hat {=}}}$ "reelle Zahl"	PD1-Glied	Verzögerung, PT1-Glied
$G_{3}(s)=T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1$ $s_{n3_{1}}=-\delta +j\omega ;\ s_{n3_{2}}=-\delta -j\omega$	PD2-Glied: für 0 < D < 1 mit konjugiert komplexen Nullstellen	Schwingungsglied PT2-Glied: für 0 < D < 1 mit konjugiert komplexen Polen

Dabei ist T die Zeitkonstante, s die komplexe Frequenz, D der Dämpfungsgrad.

• Beispiel einer Übertragungsfunktion der Polynomdarstellung und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:

$G_{1}(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s+a_{0}}}:=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{(s-s_{p1})(s-s_{p2})\dotsm (s-s_{pn})}}$

Sind in der Polynomdarstellung alle Ableitungen und zugehörige Koeffizienten lückenlos mit positivem Vorzeichen vorhanden, stellt die Übertragungsfunktion für die Exponenten n > m ein zeitverzögerndes asymptotisch stabiles System dar. Werden negative Werte der Pole und Nullstellen eingesetzt, entstehen positive Linearfaktoren.

Das Gesamtsystem wird als "globales proportionales Systemverhalten" bezeichnet.

Beispiel: Bestimmung des Pols eines Linearfaktors $G(s)=s+3$ im Nennerpolynom:

$s+3=0;\quad s\ {\mathrel {\hat {=}}}\ s_{p}=-3$

• Beispiel einer Übertragungsfunktion der Polynomdarstellung ohne Absolutglied im Nennerpolynom und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:

Der Term der gewöhnlichen Differenzialgleichung oder eines transformierten Polynoms im Zähler und Nenner der Übertragungsfunktion mit den Koeffizienten $a_{0}$ und $b_{0}$ wird allgemein als Absolutglied bezeichnet. Für $a_{0}=0$ oder $b_{0}=0$ gilt:

$G(s)=s-0=s$

Linearfaktor ohne Absolutglied $a_{0}$ des Polynoms im Nenner, Pol $s_{p1}=0$.

$G_{2}(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s}}:=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{s(s-s_{p2})\dotsm (s-s_{pn})}}$

Fehlt das Absolutglied a₀ im Nennerpolynom (a₀ = 0), kann die Variable s aus dem Nennerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales integrierendes Systemverhalten" bezeichnet. Fehlt das Absolutglied b₀ im Zählerpolynom (b₀ = 0), kann die Variable s aus dem Zählerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales differenzierendes Systemverhalten" bezeichnet.

• Beispiel einer Übertragungsfunktion in der Pol-Nullstellen-Darstellung mit einem konjugiert komplexen Pol im Nennerpolynom:

Bei dynamischen Systemen 2. Ordnung (z.B. Feder-Masse-Dämpfungssystem) oder bei Systemen 1. Ordnung, die eine positive Rückführung enthalten (Regelkreise), kann ein Energieaustausch stattfinden. Solche Systeme mit konjugiert komplexen Lösungen der Pole und Nullstellenkönnen können in einem Gesamtsystem enthalten sein und treten immer paarweise - meist im Nenner der Übertragungsfunktion - mit einem identischen Realteil $\delta$ auf.

$s_{n1}=-\delta +j\omega$ $\$ und $\$ $s_{n2}=-\delta -j\omega \,$, oder zusammengefasst

$s_{n1;2}=-\delta \pm j\omega$

Die Polynome mit konjugiert komplexen Nullstellen werden zur einfacheren Berechenbarkeit zu quadratischen Termen zusammengefasst, in denen nur reelle Koeffizienten auftreten. Deshalb lässt sich ein Elementarsystem 2. Ordnung mit konjugiert komplexen Polen und Nullstellen nicht in 2 Linearfaktoren 1. Ordnung mit nur reellen Koeffizienten zerlegen.

$G_{3}(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s+a_{0}}}:=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{[s-(\delta +j\omega )]\cdot [s-(\delta -j\omega )]\dotsm (s-s_{pn})}}$

Wird der Klammerausdruck mit den komplexen Größen im Nenner aufgelöst, entsteht:

$G(s)=[s-(\delta +j\omega )]\cdot [s-(\delta -j\omega )]=s^{2}-2\cdot \delta \cdot s+\delta ^{2}+\omega ^{2}\ :=s^{2}-p\cdot s+q\ {\bigg |}\qquad p=2\cdot \delta$ und $q=\delta ^{2}+\omega ^{2}$

$G_{3}(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s+a_{0}}}:=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{(s^{2}-2\cdot \delta \cdot s+\delta ^{2}+\omega ^{2})\dotsm (s-s_{pn})}}:=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{(s^{2}-p\cdot s+q)\dotsm (s-s_{pn})}}$

Wenn Zahlenwerte vorliegen, können mit verschiedenen Methoden, wie mit der pq-Formel $x^{2}+px+q=0$ für Systeme 2. Ordnung, oder fertige im Internet verfügbare Programme bis 4. Ordnung mit dem Aufruf - "Nullstellen (Lösungen) von Polynomen bestimmen" - die Pole und Nullstellen bestimmt werden.

Für Systeme mit Polynomen 2. Ordnung der Form $s^{2}+p\cdot s+q=0\,$ errechnen sich die Nullstellen bzw. die Pole:

$s_{p1;2}=-{\frac {p}{2}}\pm {\sqrt {{\frac {p^{2}}{4}}-q}}$

Wenn das Polynom 2. Ordnung $(s^{2}-2\cdot \delta \cdot s+\delta ^{2}+\omega ^{2})=0$ in die Form zur Lösung einer gemischt quadratischen Gleichung gebracht wird, lassen sich die Nullstellen für p und q durch Faktorenvergleich bestimmen. $p=2\cdot \delta$ wird positiv, wenn negative Realteile von $s_{p}$ oder $s_{n}$ vorliegen.

Die Pol- Nullstellendarstellung der Übertragungsfunktion für ein asymptotisch stabiles System enthält immer positive Zahlenwerte, was voraussetzt, dass die Pole und Nullstellen negative Realteile enthalten.

Zeitkonstantendarstellung

Es existieren 2 faktorielle Darstellungsformen, die Pol-Nullstellen-Darstellung und die Zeitkonstanten-Darstellung. Die Zeitkonstanten-Darstellung hat einen höheren Anschauungswert und den Vorteil, dass bei Änderung der Zeitkonstante sich die Systemverstärkung nicht ändert.

Bei der Zeitkonstantendarstellung wird der Produktterm s - s_n so umgestellt, dass der Reziprokwert 1/s_n = T gebildet wird.

Der Produktterm in der Zeitkonstanten-Darstellung mit negativem Wert der Polstelle s_P (Term im Nenner asymptotisch stabiles System) lautet damit:

$\underbrace {(s-s_{p})} _{Produktterm}=\ \underbrace {s_{p}\cdot ({\frac {1}{s_{p}}}\cdot s+1)} _{s_{p}\,=\,negativer\ Wert}\quad :=\underbrace {K\cdot (T\cdot s+1)} _{Zeitkonstantendarstellung}$.

Bei der Zeitkonstanten-Darstellung des Linearfaktors werden die zwei Terme positiv dargestellt. Dies setzt voraus, dass die Realanteile der zugehörigen Nullstellen und Pole negativ sind.

Rechenbeispiel einer Übertragungsfunktion G(s) 3. Ordnung mit konjugiert komplexen Polen im Nenner

Gegeben: Übertragungsfunktion 3. Ordnung in Polynomdarstellung $G(s)={\frac {Y(s)}{U(s)}}={\frac {s+5}{s^{3}+8\cdot s^{2}+37\cdot s+50}}$ Gesucht: Übertragungsfunktion in der Pol- Nullstellendarstellung. Übertragungsfunktion in der Zeitkonstanten-Darstellung. Lösung: Bestimmung der Nullstellen und Polstellen der Polynome: durch Anwendung eines Rechenprogrammes aus dem Internet. [Suchbegriff: "Nullstellen (Lösungen) von Polynomen" unter Google]: Nullstelle: $s_{n1}=-5$ Polstelle: $s_{p1}=-2$ Polpaar: $s_{p2;3}=-\delta \pm j\omega =-3\pm j4$ Bei einem Polynom mit konjugiert komplexen Polen im Nenner einer Übertragungsfunktion handelt es sich um ein Teilsystem mit der Bezeichnung $PT2_{kk}\,$ -Schwingungsglied. Bestimmung der Linearfaktoren aus den Polen und Nullstellen: Nullstellen und Pole Linearfaktoren Nullstelle: $s_{n1}=-5$ $G_{n1}(s)=s+5$ Polstelle: $s_{p1}=-2$ $G_{p1}(s)=s+2$ Polpaar: $s_{p2;3}=-3\pm j4$ mit $p=2\cdot \delta =2\cdot -3=-6$ mit $q=\delta ^{2}+\omega ^{2}=3^{3}+4^{2}=25$ $G_{p2;3}(s)=s^{2}-2\cdot \delta \cdot s+\delta ^{2}+\omega ^{2}\ =\ s^{2}+6\cdot s+25$ Übertragungsfunktion in der Pol- Nullstellen-Darstellung $G(s)={\frac {Y(s)}{U(s)}}={\frac {s+5}{(s+2)\cdot (s^{2}+6\cdot s+25)}}$ Übertragungsfunktion in der Zeitkonstanten-Darstellung $G(s)={\frac {Y(s)}{U(s)}}={\frac {5\cdot (0,2\cdot s+1)}{2\cdot 25\cdot (0,5\cdot s+1)\cdot (0,04\cdot s^{2}+0,24\cdot s+1)}}={\frac {0,1\cdot (0,2\cdot s+1)}{(0,5\cdot s+1)\cdot (0,04\cdot s^{2}+0,24\cdot s+1)}}$

Anmerkung: Ein zu Null gesetztes Polynom kann beliebig mit Zahlen multipliziert oder dividiert werden, die Nullstellen sind immer identisch. Faktoren von zerlegten Polynomen in Produkte müssen berücksichtigt werden, anderenfalls sind Polynom und Produkte nicht identisch.

Negative reelle Pole und Nullstellen bedeuten Systemstabilität des betreffenden Übertragungsgliedes im s-Bereich. Negative konjugiert komplexe Polpaare bedeuten Systemstabilität als schwingendes Übertragungsglied innerhalb eines bestimmten Dämpfungsbereichs D.

Die Art der Pole einer Übertragungsfunktion bestimmt das Zeitverhalten eines Systems. Nullstellen der Übertragungsfunktion haben nur Einfluss auf die Systemamplituden.

Darstellungsformen der Übertragungsfunktion

Aus der Laplace-Transformation einer systembeschreibenden Differenzialgleichung entsteht die Grundform der Übertragungsfunktion G(s) in Polynom-Darstellung. Daraus lassen sich weitere bekannte Schreibweisen der Übertragungsfunktionen errechnen, die unterschiedliche Eigenschaften für die Berechnung der Ausgangsgröße y(t) im Zeitbereich des Übertragungssystems G(s) bei gegebenem Eingangssignal U(s) aufweisen. Alle Formen der Übertragungsfunktionen sind mathematisch bei Rückrechnung mit der Polynomdarstellung identisch.

Die Übertragungsfunktion stellt sich in 4 mathematische Schreibweisen mit gleichem mathematischen Inhalt dar.

• Polynomdarstellung
• Produktdarstellung (Linearfaktoren)
• Zeitkonstantendarstellung
• Partialbruchdarstellung

Diese nicht mehr aufspaltbare Produkte in Zeitkonstantendarstellung sind: (Ts), (Ts+1) und (T²s + 2DTs + 1)_KK. Sie haben ein völlig unterschiedliches Übertragungsverhalten, ob sie im Nenner (integrierend, verzögernd) oder Zähler (differenzierend) einer Übertragungsfunktion stehen.

Übertragungsfunktion	Darstellungsform im s-Bereich
Polynom-Darstellung	$G(s)={\frac {b_{m}s^{m}+\dotsb +b_{1}s+b_{0}}{s^{n}+a_{n-1}s^{n-1}+\dotsb +a_{1}s+a_{0}}}$
Pol-Nullstellen-Darstellung (Produktdarstellung)	$G(s)=k\cdot {\frac {(s-s_{n1})(s-s_{n1})\dotsm (s-s_{nm})}{(s-s_{p1})(s-s_{p2})\dotsm (s-s_{pn})}}$ s = Laplace-Operator, sn = Zahlenwert der Nullstelle, sp = Zahlenwert der Polstelle
Zeitkonstanten-Darstellung	$G(s)=K\cdot {\frac {(T_{V1}\cdot s+1)(T_{V2}\cdot s+1)\dotsm (T_{Vm}\cdot s+1)}{(T_{1}\cdot s+1)(T_{2}\cdot s+1)\dotsm (T_{n}\cdot s+1)}}$ Für reelle Linearfaktoren 1. Grades mit Absolutglied und negativen Pol- Nullstellen.
Partialbruch-Darstellung	$G(s)={\frac {A_{1}}{s-s_{p1}}}+{\frac {A_{2}}{s-s_{p2}}}+\dotsb +{\frac {A_{n}}{s-s_{pn}}}$ Für reelle Linearfaktoren 1. Grades mit Absolutglied.

Die Zerlegung der Zähler- und Nennerpolynome der Übertragungsfunktion in je eine Produktform (Linearfaktoren) gestattet eine einfache detaillierte Interpretation des Systemverhaltens und der Bestimmung der Koeffizienten des Übertragungssystems. Diese Zerlegung in Linearfaktoren erfolgt durch die Bestimmung der Nullstellen der Polynome.

Die Linearfaktoren, als kleinste Systemeinheit der Produktdarstellung der Polynome, haben konträre Signaleigenschaften, je nachdem, ob sie im Zähler oder im Nenner der Übertragungsfunktion stehen. Stehen sie im Zähler, haben sie eine differenzielle voreilende Signalwirkung des Systemausgangs, stehen sie im Nenner haben sie eine integrierende bzw. verzögernde Signalwirkung.

Linearfaktoren mit gleichen Zeitkonstanten und gleicher Verstärkung im Zähler und Nenner können sich theoretisch zum Übertragungsverhalten G(s) = 1 kompensieren. In der Regelungstechnik wird dieses Verhalten zum Reglerentwurf in einem Regelkreis als sogenannte Pol- Nullstellenkompensation genutzt.

Die Übertragungsfunktion:

$G(s)={\frac {Y(s)}{U(s)}}:={\frac {{\text{Zähler}}(s)}{{\text{Nenner}}(s)}}$

eines dynamischen Übertragungssystems kann einfache und mehrfache Linearfaktoren im Zähler und Nenner enthalten. Derartige Systeme beschreiben das Frequenzverhalten mit der komplexen Frequenz $s=\delta +j\omega$ mit einem Systemeingang $U(s)$ und einen Systemausgang $Y(s)$.

Darstellung der Übertragungsfunktion als Produktterme (Linearfaktoren)

Der eigentliche Vorteil der Produkt-Darstellung von Übertragungsfunktionen G(s) mittels Nullstellenbestimmung liegt darin, dass praktisch alle vorkommenden regulären (stabilen) und nichtregulären (instabilen) Übertragungsfunktionen bzw. Frequenzgänge von Übertragungsgliedern G auf folgende drei Grundformen 1. und 2. Ordnung geschrieben bzw. zurückgeführt werden können. Stehen die Grundglieder im Zähler, haben sie eine differenzierende Wirkung, stehen sie im Nenner, haben sie eine verzögernde (speichernde) Wirkung:

Typ Übertragungsfunktion	Bedeutung im Zähler	Bedeutung im Nenner
$G1(s)=T\cdot s$ Linearfaktor ohne Absolutglied	Differenzierer, D-Glied	Integrator, I-Glied
$G2(s)=T\cdot s+1$ Linearfaktor mit Absolutglied	PD-Glied	Verzögerung, PT1-Glied
$G3(s)=T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1$	PD2-Glied: für 0 < D < 1 mit konjugiert komplexen Nullstellen	Schwingungsglied PT2-Glied: für 0 < D < 1 mit konjugiert komplexen Polen
Nichtphasenminimales (nichtreguläres) System $G2^{*}(s)=T\cdot s-1$	PD-Glied mit positiver Nullstelle (hat keine technische Bedeutung)	Instabile Verzögerung PT1-Glied mit einer positiven Polstelle
Nichtphasenminimales (nichtreguläres) System $G3^{*}(s)=T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s-1$	PD-Glied 2. Ordnung mit einer negativen und positiven Nullstelle (hat eine Bedeutung als Vorfilter i. d. Regelungstechnik)	Instabiles Schwingungsglied PT2-Glied mit einer negativen und positiven Polstelle

Dabei ist T die Zeitkonstante, s die komplexe Frequenz bzw. die Laplace-Variable, D der Dämpfungsgrad.

Prinzipielle Anwendung der Übertragungsfunktion für den Reglerentwurf

Die Übertragungsfunktion des geschlossenen Regelkreises ergibt sich durch algebraische Berechnung der Regelkreiskomponenten für die Kreis-Schließbedingung. Die sich so ergebenden Polynome der Übertragungsfunktion werden durch Bestimmung der Pole und Nullstellen in die Produktdarstellung überführt. Die Lage der Pole im s-Diagramm bestimmt die Stabilität des Regelkreises.

Rechenbeispiel zur Bestimmung der Übertragungsfunktion aus der systembeschreibenden Differenzialgleichung

Darstellung der Sprungantwort eines PT2-Schwingungsgliedes,
Dämpfung D = 0,125.

Differenzialgleichung 3. Ordnung gegeben: $0,5\cdot y^{(3)}(t)+0,5\cdot {\ddot {y}}(t)+2,125\cdot {\dot {y}}(t)+y(t)=2\cdot {\dot {u}}(t)+u(t)\,$ Gesucht Übertragungsfunktion in Zeitkonstantendarstellung, Beschreibung des Systemverhaltens im Zeitbereich, Sprungantwort des Systems im Zeitbereich Die Polynomgleichung ergibt sich durch die Anwendung der Laplace-Transformation der Differenzialgleichung. $0,5\cdot s^{3}\cdot Y(s)+0,5\cdot s^{2}\cdot Y(s)+2,125\cdot s\cdot Y(s)+Y(s)\quad =\quad 2\cdot s\cdot U(s)+U(s)\,$ Durch Ausklammern des Verhältnisses von Ausgangs- zum Eingangssignal der Polynomgleichung entsteht die Übertragungsfunktion. Die verbleibenden Terme der Polynomgleichung bilden die Übertragungsfunktion G(s). $G(s)={\frac {Y(s)}{U(s)}}={\frac {2\cdot s+1}{0,5\cdot s^{3}+0,5\cdot s^{2}+2,125\cdot s+1}}$ Bestimmung der Nullstellen und Polstellen der Polynome durch Anwendung eines Rechenprogrammes aus dem Internet. [Suchbegriff: "Nullstellen (Lösungen) von Polynomen unter Google]: Nullstelle: $s_{n1}=-0,5$ Polstelle: $s_{p1}=-0,5$ Polpaar: $s_{p2/3}=-0,25\pm j\cdot 1,984$ Bildung der Produktdarstellung der Übertragungsfunktion: Reelle Pole und Nullstellen bilden Linearfaktoren 1. Ordnung. Konjugiert komplexe Polpaare bilden Linearfaktoren 2. Ordnung. Sie lassen sich nicht weiter aufspalten. Allgemeine Form der Produktdarstellung mit Linearfaktoren 1. Ordnung: $G(s)={\frac {Y(s)}{U(s)}}={\frac {(s-s_{n1})\cdot (s-s_{n2})\cdot (s-s_{n3})...}{(s-s_{P1})\cdot (s-s_{P2})\cdot (s-s_{P3})...}}$ Werden negative Zahlenwerte der Nullstellen und Polstellen in diese Gleichung eingesetzt, werden die Produkte (Linearfaktoren) positiv und die Übertragungsfunktion verhält sich im Zeitbereich stabil. Der noch nicht bekannte Produktterm mit dem Linearfaktor 2. Ordnung kann errechnet werden, in dem das ursprüngliche Nennerpolynom durch den Term mit dem bekannten reellen Pol (s+0,5) dividiert wird. Das gesuchte Ergebnis ergibt sich durch normales Bruchrechnen, bei dem jeder Produktterm nacheinander durch den Diviser dividiert wird. ${\frac {0,5\cdot s^{3}+0,5\cdot s^{2}+2,125\cdot s+1}{s+0,5}}=0,5\cdot s^{2}+0,25\cdot s+2$ Damit entsteht die Übertragungsfunktion G(s) aus der systembeschreibenden Differenzialgleichung in Zeitkonstantendarstellung: $G(s)={\frac {2\cdot s+1}{0,5\cdot (2\cdot s+1)\cdot 2\cdot (0,25\cdot s^{2}+0,125\cdot s+1)}}$ Das PD1-Glied im Zähler der Übertragungsfunktion kompensiert sich mit dem PT1-Glied im Nenner der Übertragungsfunktion zu 1. Aus der Differenzialgleichung 3. Ordnung entsteht (zufällig oder gewollt) durch Kompensation ein Übertragungssystem 2. Ordnung, das als PT2-Schwingungsglied oder PT2KK-Glied (kk = konjugiert komplex)) bezeichnet wird. Übertragungsfunktion G(s) der systembeschreibenden Differenzialgleichung in Zeitkonstantendarstellung: $G(s)={\frac {1}{0,25\cdot s^{2}+0,125\cdot s+1}}$ Aus der allgemeinen Übertragungsfunktion G(s) des schwingfähigen Verzögerungsgliedes mit konjugiert komplexem Polpaar lassen sich weitere Kennwerte des Systems ermitteln: Wenn das Nennerpolynom der oben genannten Form für die Dämpfung D einen Wert 0<D<1 aufweist, hat es konjugiert komplexe Pole. Diese Form des PT2-Gliedes bezeichnet man als Schwingungsglied. Schwingungsglieder entstehen durch Energieaustausch von zwei speicherfähigen Verzögerungsgliedern 1. Ordnung, wie Feder-Masse-Systeme, LC-Schwingkreis. Allgemeine Form der Übertragungsfunktion der Schwingungsgleichung in Zeitkonstantendarstellung: $G(s)={\frac {1}{T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1}}$ Durch Koeffizientenvergleich lassen sich folgende Werte aus der Schwingungsgleichung ermitteln. Zeitkonstante T: $T={\sqrt {0,25}}=0,5$ Dämpfungswert D: $2\cdot D\cdot T=0,125\,$ $D={\frac {0,125}{2\cdot 0,5}}=0,125$ Aus der Polynomdarstellung einer Übertragungsfunktion 2. Ordnung kann nicht erkannt werden, ob es sich um ein schwingfähiges System (Schwingungsglied) oder um ein System mit 2 Verzögerungsgliedern je 1. Ordnung handelt. Ergibt die Nullstellenbestimmung anstelle von konjugiert komplexen Polen zwei reelle Pole, dann lautet die Übertragungsfunktion in Zeitkonstantendarstellung: Beispiel der Übertragungsfunktion in Zeitkonstantendarstellung mit reellen Polen und der Verstärkung K: $G(s)=K\cdot {\frac {1}{(T_{1}\cdot s+1)\cdot (T_{2}\cdot s+1)}}$

Testsignale

Den Testsignalen ist gemeinsam, dass sie zum Zeitpunkt t = 0 beginnen und bei t < 0 eine Amplitude = 0 aufweisen. Es wird das Testsignal im s-Bereich als Eingangsgröße U(s) an einem Übertragungssystem und die Systemantwort als Ausgangsgröße Y(s) in der nachfolgenden Tabelle dargestellt. Zur Unterscheidung der Funktion der Signale werden sie mit den Zeichen δ (Impulsfunktion), Ϭ (Sprungfunktion), a (Rampenfunktion) und $\sim$ (Sinusfunktion) indiziert.

Die Ausgangsgröße y(t) eines linearen dynamischen Systems kann für ein gegebenes Eingangssignal u(t) bestimmt werden, wenn $Y(s)=U(s)\cdot G(s)$ berechnet wird und in Laplace-Transformationstabellen für Y(s) z. B. in Zeitkonstanten-Darstellung die korrespondierende Gleichung der Zeitfunktion ermittelt wird.

Die Laplace-Transformation der Standard-Eingangssignale f(t) wie Impuls-, Sprung-, Rampen- und Sinusfunktionen stellen sich wie folgt dar:

Eingangssignal u(t)	Zeitverhalten des Eingangssignals	Bildbereich
Impulsfunktion δ (Stoßfunktion, Deltaimpuls)	Normierter Impuls = $\int _{0}^{\infty }{\hat {u}}_{\delta }\cdot \,dt=1;$ $\qquad$ $\qquad$ Impulsdauer = $\Delta t={\frac {1}{{\hat {u}}_{\delta }(t)}}$	$U_{\delta }(s)=1$
Sprungfunktion σ	Einheitssprung: $u_{\sigma }(t)=1;\quad {\text{für}}\ t>0;\quad u_{\sigma }(t)=0;\quad {\text{für}}\ t<0$	$U_{\sigma }(s)={\frac {1}{s}}$
Anstiegsfunktion A (Rampe)	Anstiegsfunktion: $u_{A}(t)=c\cdot t;$ $\qquad$ $\qquad$ $Gradient\ c={\frac {\Delta \,u_{A}(t)}{\Delta \,t}}$	$U_{A}(s)={\frac {1}{s^{2}}}$
Sinusfunktion $\sim$	$u_{\sim }(t)={\hat {u}}_{\sim }\cdot \sin(\omega \cdot t);\qquad \omega =2\cdot \pi \cdot f;\qquad T={\frac {1}{f}}$	$U_{\sim }(s)={\frac {\omega }{s^{2}+\omega ^{2}}}$

Berechnungsbeispiel für ein PT1-Verzögerungsglied mit einem Eingangssignal als Sprungfunktion

Sprungantwort eines PT1-Verzögerungsgliedes mit T = 2 [sec]:
$G(s)\cdot {\frac {1}{s}}={\frac {1}{s\cdot (2\cdot s+1)}}$
$y(t)=1-e^{-t/T}$

Für die Berechnung des Zeitverhaltens von Übertragungssytemen G(s) mit der Übertragungsfunktion müssen die Eingangssignale (Testsignale) u(t) für den s-Bereich definiert werden. Gegeben: Übertragungsfunktion: $G(s)={\frac {K}{(T\cdot s+1)}}$ Eingangssignal als normierte Sprungfunktion 1(t): $u_{\sigma }(t)\ \circ \!\!-\!\!\bullet \ U_{\sigma }(s)={\mathcal {L}}^{-1}\,\{{1}(t)\}={\frac {1}{s}}$ Gesucht: Suchfunktion im s-Bereich der Laplace-Transformationstabellen: $y(t)={\mathcal {L}}^{-1}\underbrace {\left\{U(s)\cdot G(s)\right\}} _{\text{Suchbegriff}}=K\cdot {\mathcal {L}}^{-1}\underbrace {\left\{{\frac {1}{s\cdot (T\cdot s+1)}}\right\}} _{\text{Suchbegriff}}$ Übergangsfunktion (Sprungantwort) im Originalbereich: Die Gleichung zur Berechnung des Zeitverhaltens des PT1-Gliedes kann direkt aus den Laplace-Transformationstabellen abgelesen werden. Die Transformationstabellen sind gelegentlich für die Übertragungsfunktionen des s-Bereiches in der Pol-Nullstellen-Darstellung oder in der Zeitkonstanten-Darstellung ausgeführt. Algebraisch sind beide Darstellungsarten identisch. Der Faktor K unterliegt nicht der Transformation und ist deshalb im s-Bereich wie auch im Zeitbereich gültig. $y(t)=K\cdot (1-e^{-t/T})$ Mit dem Einsetzen verschiedener Werte für t in die Gleichung ergibt sich ein geschlossener Funktionsverlauf für y(t). Anmerkung: Bei Übertragungsfunktionen G(s) mit konjugiert komplexen Polen oder Nullstellen können die zugehörigen korrespondierenden Zeitfunktionen sehr aufwendig sein und erfordern für die Lösungen im Zeitbereich gute trigonometrische Kenntnisse. Einfacher bei solchen Systemen ist die numerische Berechnung mit der diskreten Zeit $\Delta t$.

→ Siehe das ausführliche Hauptkapitel "Einführung in die Systemtheorie/ Übertragungsfunktion".

Einführung Frequenzgang

Der Frequenzgang ist ein Spezialfall der Übertragungsfunktion. Er beschreibt das Ausgangs- Eingangs- Signalverhalten eines Übertragungssystems für ausschließlich periodische sinusförmige Eingangssignale. Setzt man für die komplexe Variable $s=\delta +j\omega$ den Realteil $\delta$ zu Null, so geht die komplexe Übertragungsfunktion G(s) in den komplexen Frequenzgang

$G(j\omega )={\frac {Y(j\omega )}{U(j\omega )}}$

über, der physikalisch interpretiert und gemessen werden kann.

Beide mathematischen Begriffe der Übertragungsfunktion und des Frequenzgangs unterscheiden sich nur durch die Entstehungsweise. Sie können je nach Aufgabenstellung als Übertragungsfunktion im s-Bereich $s=\delta +j\omega$ oder als Frequenzgang mit $s=j\omega$ geschrieben werden.

Die bekanntesten Anwendungen des Frequenzgangs eines dynamischen Systems sind die grafischen Stabilitätsanalysen mittels des Bode-Diagramms und der Ortskurve des Frequenzgangs der vom amerikanischen Physiker Harry Nyquist entwickelten Stabilitätskriterien. Diese Verfahren dienen heute mehr dem Verständnis von Teilgebieten der Systemtheorie, sind aber keine Alternativen zur numerischen Berechnung eines Regelkreises, bei dem tabellarisch das innere Teil-Systemverhalten für jede Berechnungsfolge y(k•Δt) dargestellt und grafisch der zeitliche Signalverlauf verschiedener Ausgangsgrößen für eine beliebige Eingangsgröße gezeigt wird.

Ein wichtiges Anwendungsgebiet bei der experimentelle Systemidentifikation ist das Bode-Diagramm, in dem für ein unbekanntes dynamisches System durch eine frequenzvariable Einspeisung der Frequenzgang messtechnisch aufgenommen wird. Durch Bestimmung der Asymptoten an den Eckfrequenzen im Bode-Diagramm kann die Übertragungsfunktion G(s) des Systems ermittelt werden.

Einführung "Zeitdiskrete Systemmodelle"

Relativ einfache Übertragungssystem-Strukturen mit nichtlinearen Elementen, Begrenzungseffekten und Totzeitsystemen sind durch konventionelle Rechenmethoden im kontinuierlichen Zeitbereich nicht mehr geschlossen lösbar. Abhilfe bietet die numerische Berechnung im diskreten Zeitbereich Δt. Derartige Modellberechnungen insbesondere bei Systemen höherer Ordnung, linear oder nichtlinear, ohne und mit Anfangswerten sind besonders anschaulich verständlich, weil sie das Zeitverhalten einer Kette von Einzelsystemen für einen kleinen Zeitschritt tabellarisch beschreiben, so wie sich das Übertragungssystem auch in der Realität als Kette von Einzelsystemen darstellt.

Für die Berechnung des Eingangs-Ausgangsverhaltens von Übertragungssystemen oder der Simulation von Regelkreisen bieten sich käufliche Rechenprogramme an. Mit den bekannten Programmen wie MATLAB und Simulink stehen umfangreiche Befehlssätze für die theoretische Modellierung von dynamischen Systemen und vielen speziellen regelungstechnischen Befehlen zur Verfügung.

Alternativ können mit selbst erstellten beliebigen Rechenprogrammen für Differenzengleichungen mit der diskreten Zeit Δt (auch Abtastzeit T_A) in Verbindung mit logischen Operationen sehr effizient lineare und nichtlineare System-Simulationen durchgeführt werden.

Nichtlineare Übertragungssysteme sind häufig Unikate. In Kombination mit linearen dynamischen Systemen können sie meist als zeitunabhängiges Übertragungssystem vom zeitabhängigen Übertragungssystem abgetrennt und mit logischen Befehlen wie WENN-DANN-Sonst-Anweisungen oder mit Tabellenanweisungen beschrieben werden.

Systembeschreibungen: Differenzialgleichungen, Übertragungsfunktionen und Differenzengleichungen

Die mathematischen Beschreibungen linearer dynamischer Systeme mit Differenzialgleichungen, Übertragungsfunktionen und Differenzengleichungen sind untereinander austauschbar, wenn sie nur je ein totzeitfreies lineares dynamisches System mit konstanten Koeffizienten im Zeitbereich, im komplexen Frequenzbereich und numerisch im zeitdiskreten Bereich beschreiben sollen. Jede mathematische Form der Beschreibungen kann in die jeweils andere Form der partikulären Lösung der DGL, der Übertragungsfunktion (Lösung ist immer partikulär) und der numerisch lösbaren Differenzengleichung übertragen werden.

Die Lösungswege der mathematischen Gleichungen für den Verlauf des Ausgangssignals bei einem gegebenen Eingangssignal sind wie folgt höchst unterschiedlich und von unterschiedlichen Schwierigkeitsgraden:

Systembeschreibung	Mathematische Lösung im Zeitbereich	Kommentar
Differenzialgleichung	1. Gesamtlösung = Homogene Lösung + Partikuläre Lösung 2. Homogene Lösung: $y_{H}(t)=C_{1}\cdot e^{{\lambda }_{1}\cdot t}+C_{2}\cdot e^{{\lambda }_{2}\cdot t}+C_{3}\cdot e^{{\lambda }_{3}\cdot t}+\cdots$ 3. Partikuläre Lösung für $y_{p}(t)\,$ der DGL über das Faltungsintegral.	1. Homogene Lösung bezieht sich nur auf Anfangswerte, $\quad$ partikuläre Lösung nur auf Eingangssignale. 2. Umständliche Berechnung der Integrationskonstanten C. 3. Partik. Lösung mit Faltungsintegral > 2. Ordnung sehr schwierig.
Übertragungsfunktion	Mit Hilfe der inversen Laplace-Transformationstabellen oder der Anwendung der Partialbruchzerlegung.	* Kann aufwendige trigonometrische Berechnung bei Schwingungsgliedern bedeuten. * Die Partialbruchzerlegung erfordert Spezialkenntnisse und Übung .
Differenzengleichung	Die numerische Berechnung erfolgt schrittweise im Abstand der diskreten Zeit Δt. Die Gleichung wird mit $k=(0;1;2;3\cdots k_{max})$ Berechnungsfolgen wiederholt berechnet. Jede Ausgangsgröße $y_{(k)}\,$ wird zur nächsten Berechnungsfolge zur Eingangsgröße $y_{(k-1)}\,$.	* Relativ einfach, insbesondere auch bei Systemen höherer Ordnung. * Das Gleichungssystem kann leicht erweitert werden für nichtlineare Funktionen und Totzeitsysteme. * Ergebnis: Tabellarische Darstellung aller Berechnungsfolgen. * Berechnung von Anfangswerten über die Regelungsnormalform.

Lineare Übertragungsglieder werden gerne bevorzugt als Übertragungsfunktionen G(s) möglichst in Zeitkonstantendarstellung benannt, weil sie als mathematisches Modell sehr einfach und übersichtlich dargestellt werden können, obwohl sie sich nicht auf den Zeitbereich sondern auf den komplexen Frequenzbereich beziehen.

Die Übertragungsfunktion G(s) entsteht durch die Laplace-Transformation von gewöhnlichen systembeschreibenden Differenzialgleichungen. Durch die Zerlegung der Polynome der Übertragungsfunktion im Zähler und Nenner als Linearfaktoren lässt sich nachweisen, dass lineare Übertragungssysteme nur 3 Formen von Linearfaktoren und deren Vielfache je im Zähler und Nenner der Polynomgleichung enthalten.

Für das einfachste Verfahren der der numerischen Berechnung - das "Euler-Streckenzugverfahren" - werden nur zwei Formen von Differenzengleichungen 1. Grades - Linearfaktor mit und ohne Absolutglied - je im Zähler oder Nenner der Übertragungsfunktion benötigt. Für diese 4 Formen der Übertragungsfunktionen in Zeitkonstantendarstellung, die den Differenzialgleichungen 1. Ordnung entsprechen, können zeitdiskrete Differenzengleichungen erstellt werden. Alle linearen Systeme G(s) beliebiger Ordnung - auch solche mit konjugiert komplexen Polen und Nullstellen (Beispiel Schwingungsglieder) - können mit diesen vier Arten von Differenzengleichungen berechnet werden.

Ein technisches lineares dynamisches System ohne Totzeit kann durch Teilsysteme (Linearfaktoren 1. Ordnung) vollständig beschrieben werden. Die Teilsysteme können beliebig multiplikativ, additiv oder zurückgekoppelt vermascht sein.

Tabelle der regulären (phasenminimalen) Übertragungsfunktionen 1. Ordnung in Zeitkonstanten-Darstellung :

Übertragungsfunktion G(s)	$=K$	$={\frac {1}{T\cdot s}}$	$=T\cdot s$	$=K\cdot (T\cdot s+1)$	$={\frac {K}{T\cdot s+1}}$
Übergangsfunktion y(t) (Sprungantwort)
Benennung	P-Glied	I-Glied	D-Glied	PD1-Glied	PT1-Glied

Anmerkung: Bei Linearfaktoren ohne Absolutglied wie das D-Glied und das I-Glied entsprechen die Zeitkonstanten T und 1/T dem Proportionalitätsfaktoren K.

Für jedes dieser genannten zeitabhängigen Teilsysteme kann eine Differenzengleichung erstellt werden.

Verfahren der numerischen Berechnung mit Differenzengleichungen

Viele technische Übertragungssysteme bzw. Modelle der Übertragungssysteme verarbeiten kontinuierliche Eingangssignale und liefern auch kontinuierliche Ausgangssignale, dennoch können diese Übertragungssysteme aus linearen und nichtlinearen Teilsystemen bestehen.

Zeitdiskrete lineare dynamische Systeme sind dadurch gekennzeichnet, dass die inneren Systemzustände nur zu einzelnen Zeitpunkten definiert sind und an den Ein- und Ausgängen zeitdiskrete Signale auftreten. Sie spielen im Rahmen der Informationstechnik und digitalen Signalverarbeitung eine bedeutende Rolle und werden in Form von Berechnungsfolgen beschrieben.

Berechnungsfolgen mit der Folge $k=(0;1;2;3;\cdots k_{MAX})$ berechnen eine Gleichung mit der Ausgangsgröße $y_{(k-1)}$ aus einem alten Zustand zu einem neuen Zustand der Ausgangsgröße $y_{(k)}$ mit dem zeitlichen Abstand der diskreten Zeit $\Delta t$.

Für jedes Teilsystem ist die Ausgangsgröße die Eingangsgröße des nachfolgenden Systems. Parallelgeschaltete Systeme werden hintereinander berechnet, haben aber das gleiche Eingangssignal, deren Ausgangssignale werden addiert.

Diese Art der schrittweisen Berechnung eines Systems mit der Annäherung an die analytische Funktion des Systems wird als rekursiv (lat.: recurrere: zurücklaufen) bezeichnet. Die Genauigkeit der Annäherung an die analytische Funktion steigt mit dem Verhältnis des Quotienten der dominanten Systemzeitkonstante $T_{D}\,$ zur diskretisierten Zeit Δt.

Die den Übertragungsfunktionen G(s) zugehörigen Differenzengleichungen berechnen die Systemausgangsgröße $y_{(k\cdot \Delta t)}$ im Zeitbereich für definierte Zeitintervalle für eine gegebene Eingangsgröße $u_{(k\cdot \Delta t)}$. Als vereinfachte Schreibweisen für zeitdiskrete Signale gelten die Indizierungen für die aktuelle Größe $y_{(k)}$ und für eine zurückliegenden Folge $y_{(k-1)}$.

Genauigkeit der numerischen Berechnung und numerische Stabilität:

• Numerische Stabilität

Zur Vermeidung der numerischen Instabilität kann die Verstärkung nicht unbegrenzt hoch gewählt werden, wenn es auch theoretisch bei stetig wirkenden Regelkreisen bis zu zwei Verzögerungsgliedern möglich wäre.

Bedingung: Bei sehr großer Kreisverstärkung K einer Regelkreisnachbildung muss $\Delta t$ kleiner als $T_{D}/K$ sein.

$K$ ist das Produkt aller Einzelverstärkungen, $T_{D}$ ist die dominante Systemzeitkonstante.

• Genauigkeit der numerischen Simulation

Die Genauigkeit steigt mit kleiner werdendem Zeitintervall $\Delta t$ gegenüber der dominanten Systemzeitkonstante $T_{D}$. Der Approximationsfehler $F_{A}$ im Vergleich zur analytische Funktion beträgt $F_{A}\approx {\frac {\Delta t\cdot 100}{T_{D}}}\ [\%]$.

Das Zeitintervall $\Delta t$ muss kleiner als die kleinste zu berechnende Systemzeitkonstante betragen. Anderenfalls treten zusätzliche Fehler auf.

Andere Methoden der numerischen Berechnung bedienen sich zur besseren Approximation z. B. an Stelle des Rechteck-Verfahrens (Explizites Eulerverfahren) des Trapezflächenverfahrens (Heun-Verfahren), des Mehrschrittverfahrens (Runge-Kutta-Verfahren) und anderer Verfahren.

Grund der aufwendigeren Approximationsverfahren ist die erzielbare höhere Genauigkeit und damit Reduzierung der Rekursionsfolgen, was bei langsamen Rechnern bei Echtzeitberechnungen erforderlich sein kann.

Schreibweise der Differenzengleichungen

Differenzengleichungen entstehen durch lineare gewöhnliche Differenzialgleichungen, deren Differentialquotienten durch Differenzenquotienten ersetzt werden.

Bei der Anwendung zur Lösung einer Differenzialgleichung über die Übertragungsfunktion mit Hilfe der inversen Laplace-Transformation wird die analytische Lösung im Zeitbereich über den Suchbegriff in der Laplace-Transformationstabelle in Operatorenschreibweise gefunden.

Allgemein gilt für die inverse Transformation vom s-Bereich in den Zeitbereich der Suchbegriff:

$y(t)={\mathcal {L}}^{-1}\underbrace {\left\{G(s)\cdot U(s)\right\}} _{Suchbegriff}$

Die numerische Berechnung einer Differenzengleichung eines Teilsystems (Linearfaktor) bedeutet eine Annäherung an die analytische Funktion des Systems und wird stets in Operatorenschreibweise dargestellt. Sie wird anders als im Umgang mit der Übertragungsfunktion schrittweise mit der Berechnungsfolge k immer neu berechnet, wobei die Ausgangsgröße des Teilsystems im nächsten Zeitzyklus die Eingangsgröße des gleichen Teilsystems ist. Die Differenzengleichungen als Beschreibung der Teilsysteme können nach einem Signalflussplan beliebig vermascht werden, die Struktur der Differenzengleichung für ein Teilsystem darf nicht verändert werden.

Beispiel einer Differenzengleichung eines Integrationsgliedes (I-Glied):

Der Integrationsalgorithmus lautet:

$y_{(k)}=y_{(k-1)}+\Delta t\cdot f[u_{(k)}]$

Differenzengleichung der Integration (I-Glied):

$y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T_{I}}}$

Beispiel der Entstehungsweise einer Differenzengleichung eines Verzögerungsgliedes (PT1-Glied)

Rechteck-Approximation eines PT1-Gliedes durch Berechnung mit einer Differenzengleichung.

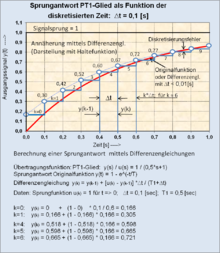
Übertragungsfunktion des PT1-Gliedes

$G(s)={\frac {Y(s)}{U(s)}}={\frac {K_{PT}}{1+s\cdot T_{1}}}={\frac {\frac {K_{PT}}{T_{1}}}{s+{\frac {1}{T_{1}}}}}$

Zugehörige Differenzialgleichung

${\dot {y}}(t)+{\frac {1}{T_{1}}}\cdot y(t)={\frac {K_{PT}}{T_{1}}}\cdot u(t)$

Der Differenzialquotient der Differenzialgleichung wird durch den Differenzenquotient ersetzt mit folgendem Ansatz:

${\frac {y_{(k)}-y_{(k-1)}}{\Delta t}}+{\frac {1}{T_{1}}}\cdot y_{(k)}={\frac {K_{PT}}{T_{1}}}\cdot u_{(k)}$

Diese Gleichung wird nach y_(k) aufgelöst. Die Differenzengleichung des PT1-Gliedes lautet:

$y_{(k)}={\frac {T_{1}}{T_{1}+\Delta t}}\cdot y_{(k-1)}+{\frac {\Delta t\cdot K_{PT}}{T_{1}+\Delta t}}\cdot u_{(k)}$

Differenzengleichung des PT1-Gliedes in vereinfachter Schreibweise mit identischer mathematischer Funktion:

$y_{(k)}=y_{(k-1)}+(K_{PT}\cdot u_{(k)}-y_{(k-1)})\cdot {\frac {\Delta t}{T_{1}+\Delta t}}$

Die tabellarische Form der numerischen Lösung erlaubt auch die Berechnung nichtlinearer statischer Systeme, indem die nichtlineare Beziehung als Wertetabelle der Tabellenspalte der Folge k zugeordnet wird. Ebenso ist die Berechnung der Totzeit eines Systems durch Verschiebung der Zeilen mit geeigneten Programmbefehlen möglich.

→ Siehe das ausführliche Kapitel "Einführung in die Systemtheorie/ Numerische Berechnung dynamischer Systeme".

Digitale Systemberechnung online

Offline-Berechnungen sind beispielsweise Simulationen eines Modells eines dynamischen Systems, bei dem in Abhängigkeit eines Eingangssignals das Ausgangsverhalten des Systems bei verschiedenen Parametern untersucht wird. Das Zeitverhalten des Rechners - die Rechenzeit - hat dabei keinen Einfluss auf das Rechenergebnis.

In technischen Prozessen, in denen ein Signal nicht kontinuierlich sondern zeitdiskret ist, bezeichnet man als Abtastung eines Zahlenwertes mit dem Zeittakt T_A. Derartige Systeme lassen sich nicht mit kontinuierlichen mathematischen Methoden wie die Differenzialgleichung im Zeitbereich oder mit der Übertragungsfunktion im komplexen Frequenzbereich beschreiben.

Anstelle von kontinuierlichen Signalen treten die mathematischen Methoden der zeitdiskreten Signale. Die Verfahren der Behandlung kontinuierlicher Signale ändern sich zu Verfahren der zeitdiskreten Behandlung wie folgt:

• Kontinuierliches Signal → abgetastetes Signal
• Differenzialgleichung → Differenzengleichung
• Laplace-Transformation → Z-Transformation
• Übertragungsfunktion G(s) → Z-Übertragungsfunktion G(z)

Wird ein Digitalrechner für die Steuerung eines realen stetigen Prozesses in einem Eingrößensystem eingesetzt, so werden 2 Schnittstellen benötigt. Das stetige Eingangssignal erfordert einen Analog-Digitalwandler (AD-Wandler), das digitale Ausgangssignal des Digitalrechners entweder eine Digitalanzeige oder ein Digital-Analogwandler (DA-Wandler). Mit einem Zeittakt werden Rechner und Schnittstellen synchronisiert. Der Digitalrechner simuliert mit Hilfe von Differenzengleichungen das dynamische System.

Bei Echtzeitberechnungen, beispielsweise mit einem programmierbaren digitalen Regler, der auf eine Hardware-Regelstrecke wirkt, wird die Diskretisierungszeit ∆t durch die "Abtastzeit" T_A ersetzt, mit der das meist analoge Ausgangssignal der Regelstrecke über Analog-Digitalwandler erfasst wird. Der Abtastung des Ausgangssignals ist üblicherweise ein Halteglied (Sample-and-Hold-Schaltung) nachgeschaltet, so dass ein gestufter Verlauf des Ausgangssignals entsteht. Hat das Halteglied kein Zeitverhalten, wird es als Halteglied 0. Ordnung bezeichnet.

Bei schnellen Übertragungssystemen wie Regelstrecken spielen die Systemgeschwindigkeiten des Rechners, der A/D-Wandler, die Sample-and-Hold-Schaltung, wie auch die verwendeten Differenzengleichungen beziehungsweise deren Approximations-Algorithmen eine große Rolle.

Für die Durchführung der zeitdiskreten Rechenvorgänge am Digitalrechner wird eine spezielle Form der Laplace-Transformation, die Z-Transformation verwendet.

Kurzbeschreibung Zustandsraumdarstellung

Symbolisches Blockschaltbild eines Modells eines Übertragungssystems 1. Ordnung in Zustandsraumdarstellung für ein Eingrößensystem.

Die Zustandsgrößen eines linearen dynamischen Systems beschreiben den inneren Bewegungsablauf des Systems.

Die Zustandsraumdarstellung bezieht sich auf ein Zustandsraummodell, welches meist ein Schema der Regelungsnormalform oder der Beobachtungsnormalform beschreibt. Es symbolisiert die überführte Differenzialgleichung n-ter Ordnung in n-gekoppelte Zustands-Differentialgleichungen erster Ordnung. Dabei werden sämtliche Beziehungen der Zustandsgrößen, der Eingangsgrößen und Ausgangsgrößen in Form von Matrizen und Vektoren dargestellt. Das Zustandsraummodell wird vereinfacht durch die zwei Zustandsgleichungen – der Zustandsdifferenzialgleichung und der Ausgangsgleichung – beschrieben.

Das Zustandsraummodell kann für nicht sprungfähige Systeme direkt aus den Koeffizienten der systembeschreibenden Differenzialgleichung oder der zugehörigen Übertragungsfunktion erstellt werden. Es gilt als ingenieurtechnisch geeignete Methode der Analyse und Synthese dynamischer Systeme im Zeitbereich und ist besonders effizient bei der regelungstechnischen Behandlung von Mehrgrößensystemen, nichtlinearen und zeitvariablen Übertragungssystemen.

Die Zustandsvariablen beschreiben physikalisch den Energiegehalt der in einem technischen dynamischen System enthaltenen Speicherelemente. Sie bedeuten z. B. Spannung an einem Kondensator, Strom in einer Induktivität, bei einem Feder-Massesystem die potentiellen und kinetischen Energieanteile. Die Anzahl der Zustandsvariablen $x_{1}(t)\cdots x_{n}(t)\,$ des Zustandsvektors ${\underline {x}}(t)\,$ ist die Dimension des Zustandsraumes. Im Zustandsvektor ${\underline {x}}(t)\,$ zum beliebigen Zeitpunkt t₍₀₎ sind alle Informationen des dynamischen Übertragungssystems enthalten.

Wesentliche Begriffe zum Verständnis der Beschreibung eines Übertragungssystems im Zustandsraum sind das Zustandsraummodell und die angewandte Normalform, nach der die Zustandsgleichungen und zugehörigen Matrizen / Vektoren ausgelegt sind.

Bei den Zustandsbeschreibungen mit Normalformen nehmen die Zustandsgleichungen besonders einfache und zweckmäßige Formen für bestimmte Berechnungen an. Für die Normalformen wird von der Systembeschreibung des linearen Übertragungssystems durch die Differenzialgleichung oder zugehörige Übertragungsfunktion ausgegangen.

Blockschaltbild des Signalflussplanes eines Übertragungssystems 3. Ordnung in der Regelungsnormalform.

Die bekannteste Normalform ist die Regelungsnormalform, welche grafisch die Lösung einer Differenzialgleichung beschreibt.

Die Signalstruktur der Regelungsnormalform stellt sich als ein stetiges zeitkontinuierliches System dar, dass mit der Eingangsgröße u(t) die Lösung der Differentialgleichung y(t) wiedergibt und gleichzeitig die Zustandsvariablen $x_{1}(t),x_{2}(t)\cdots x_{n}(t)$ zeigt.

Das Blockschaltbild der Regelungsnormalform zeigt die Umsetzung und Lösung der Differenzialgleichung in die physikalischen analogen Signalflüsse der Zustandsgrößen einschließlich der Ausgangsgröße bei gegebener Eingangsgröße. Man kann sie als eine Weiterentwicklung der in der Analogrechentechnik bekannten Verfahren zur Lösung einer Differentialgleichung n-ter Ordnung mit n Integratoren betrachten. Die Signalflüsse können bei Kenntnis der Koeffizienten der Zustandsvariablen direkt mittels numerischer Berechnung für beliebige Eingangssignale ermittelt und grafisch dargestellt werden.

Enthält die systembeschreibende Differenzialgleichung keine Differentiale der Eingangsgröße, bzw. die zugehörige Übertragungsfunktion hat nur Pole aber keine Nullstellen, so werden die Koeffizienten der Regelungsnormalform laut dargestelltem Blockschaltbild b1 und b2 zu Null.

Die Regelungsnormalform muss nicht zwingend in die Form von Matrizen und Vektoren dargestellt werden.

Zustandsdifferenzialgleichung und Ausgangsgleichung

Das Zustandsraummodell wird anhand der dargestellten Signalflüsse durch 2 Gleichungen beschrieben, die Zustandsdifferenzialgleichung und die Ausgangsgleichung (auch Ausgabegleichung).

Die Zustandsdifferenzialgleichung ist eine Vektordifferenzialgleichung 1. Ordnung, die die Systemdynamik beschreibt. Sie gibt an, wie das Eingangssignal u(t) die einzelnen Speicher beeinflusst und wie diese Speicher miteinander verkoppelt sind.

Die algebraische Ausgangsgleichung beschreibt, wie das Ausgangssignal y(t) mit den Systemzuständen verbunden ist.

Gleichungen des Zustandsraummodells:

Gleichung	Bei Eingrößensystemen	Bei Mehrgrößensystemen
Zustandsdifferenzialgleichung (auch Zustandsgleichung)	${\underline {x}}'(t)={\underline {A}}\cdot {\underline {x}}(t)+{\underline {b}}\cdot u(t)$	${\underline {x}}'(t)={\underline {A}}\cdot {\underline {x}}(t)+{\underline {B}}\cdot {\underline {u}}(t)$
Ausgangsgleichung	$y(t)={\underline {c}}^{T}\cdot {\underline {x}}(t)+d\cdot u(t)$ d = 0 für n > m	${\underline {y}}(t)={\underline {C}}\cdot {\underline {x}}(t)+{\underline {D}}\cdot {\underline {u}}(t)$ ${\underline {D}}\,$ = 0 für n > m

Zustandsregelung

Signalflussplan eines einfachen Zustandsreglers für eine Regelstrecke 3. Ordnung eines Eingrößensystems.

Ein Übertragungssystem in der Regelungsnormalform mit ihren Zustandsvariablen kann als Regelstrecke in einen Regelkreis eingebunden werden.

Durch die Zustandsrückführung kann keine stationäre Genauigkeit der Regelgröße zum Sollwert erreicht werden. Deshalb wird mit einem Vorfilter die Anpassung der Führungsgröße an die stationäre Ausgangsgröße hergestellt.

Für anspruchsvolle Regelaufgaben mit Systemen im Zustandsraum kann die Einführung eines überlagerten Regelkreises für den Zustandsregelkreis mit einer Ausgangsrückführung erforderlich sein. Damit sind sämtliche stationären Probleme für die Übereinstimmung der Führungsgröße mit der Regelgröße und konstante Störanteile ausgeschaltet. Das Vorfilter entfällt.

Die Zustandsregelung mit der Rückführung der Zustandsvariablen ist vergleichbar mit einer Kaskadenregelung.

Die Kaskadenregelung besteht aus hierarchisch hintereinander geschachtelten Folgeregelkreisen, die innerhalb eines überlagerten Regelkreises liegen. Diese effiziente Reglerstruktur der Kaskadenregelung ist möglich, wenn einzelne Signalgrößen von Teilsystemen einer Regelstrecke messbar sind. Diese Teilsysteme mit Verzögerungen niedriger Ordnung sind einfacher und schneller regelbar. Die Ausgangsrückführungen der Teilregelkreise entsprechen angenähert den Zustandsvariablen.

Kaskadenregler sind Hilfsgrößen-Regler innerhalb einer Folgekette. Sie erfüllen wie die Zustandsregler eine bessere Dynamik der Regelgröße und tragen zur Verbesserung des Störverhaltens bei.

→ Siehe den ausführlichen Wikipedia-Artikel Zustandsraumdarstellung

Einführung "Eingrößen- und Mehrgrößensysteme"

Blockdiagramm eines Mehrgrößensystems in Matrix / Vektor-Darstellung.

Es kann ein Signal oder es können mehrere Eingangssignale auf das System einwirken. Das System antwortet mit einem oder mit mehreren Ausgangssignalen. Diese mit einem Eingangs- und Ausgangssignal behafteten Systeme werden als Klasse der Eingrößensysteme, die mit mehreren Eingangs- und Ausgangssignalen werden als Mehrgrößensysteme bezeichnet.

Bei vielen technischen Prozessen müssen mehrere physikalische Größen gleichzeitig geregelt werden, wobei diese Größen voneinander abhängig sind. Bei Änderung einer Eingangsgröße (Stellgröße u(t)) wird zusätzlich eine andere Ausgangsgröße (Regelgröße y(t)) oder auch alle anderen Ausgangsgrößen beeinflusst.

Bei Mehrgrößen-Regelstrecken sind die Eingangsgrößen und Ausgangsgrößen untereinander verkoppelt. Im Regelkreis sind die r Eingangsgrößen der Regelstrecke U1(s) bis Ur(s) die Stellgrößen des Systems, die entsprechend dem Kopplungsgrad mehr oder weniger auf die verschiedene Anzahl m der Regelgrößen Y1(s) bis Ym(s) einwirken können.

Beispiele von einfachen Mehrgrößensystemen:

• Bei der Dampferzeugung sind Druck und Temperatur gekoppelt,
• Bei Klimaanlagen sind Temperatur und Luftfeuchtigkeit gekoppelt.

Für den einfachen Fall der Verkopplung einer Regelstrecke mit 2 Eingängen und 2 Ausgängen treten die häufigsten symmetrischen Verkopplungsarten in P- und V-Kanonische Form|kanonischer Struktur auf. Bei der P-kanonischen Struktur wirkt ein Eingang der Strecke über ein Koppelelement auf den nicht zugehörigen Ausgang der Strecke. Bei der V-kanonischen Struktur wirkt ein Ausgang der Strecke über ein Koppelelement auf den nicht zugehörigen Eingang der Strecke.

Je nach Art der gekoppelten Regelstrecken können für den Reglerentwurf 3 Konzepte gewählt werden:

• Dezentrale Regelung

Jedem Stell- und Regelgrößenpaar wird ein eigener Regler zugeordnet. Die auf diesen Regelkreis durch die Kopplung einwirkenden Störungen werden durch den Regler kompensiert. Dieses Verfahren ist bei schwacher Kopplung oder bei langsamen Koppelsystemen gegenüber der Hauptregelstrecke akzeptabel.

• Regelung mit Entkopplung

Jedem Stell- und Regelgrößenpaar wird ein Hauptregler und für die Kopplungen zwischen den Stell- und Regelgrößen je ein Entkopplungsregler zugeordnet. Es ist Aufgabe der Entkopplungsregler, den Einfluss der anderen Stellgrößen auf die jeweilige Regelgröße zu eliminieren oder zumindest zu reduzieren.

• Echte Mehrgrößenregelung

Der Mehrgrößenregler hat so viele Eingänge wie Regelgrößen und so viele Ausgänge wie Stellgrößen. Die Kopplungen zwischen den Komponenten werden in einem einheitlichen Reglerkonzept berücksichtigt. Der Entwurf der Mehrgrößenregler erfolgt über die Matrizen- Vektorrechnung.

→ Siehe Wikipedia-Artikel Regler: Abschnitt Regler für Mehrgrößensysteme

→ Siehe Wikipedia-Artikel Regelstrecke: Abschnitt Mehrgrößensysteme

Quellen

Zurück zum Inhaltsverzeichnis