Ing: Grundlagen der Elektrotechnik/ Druckversion/ Grundlagen der Schaltungsanalyse

Knotenregel und Maschenregel

Die Knotenregel (1. Kirchhoffsche Gleichung)

In einem Knoten gilt: Die Summe der zufließenden Ströme ist gleich der Summe der abfließenden Ströme.

$I_{1}+I_{4}=I_{2}+I_{3}$ (Bild 1.)

Bild 1.

Zeigen alle Zählpfeile vom Knoten weg, sind also alle Ströme abfließend definiert, so muß die Summe aller dieser Ströme Null werden.

Allgemein gilt für einen Knoten, aus dem n Ströme abfließen:

$\sum _{v=1}^{n}I_{v}=0\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (1)$

Diese Gleichung gilt nicht nur für die Summe aller abfließenden Ströme, sondern auch für die Summe aller zufließenden. Man bezeichnet sie als 1. Kirchhoffsche Gleichung.

Es sei noch gesagt, dass die Gl.(1) nicht nur für einen einzelnen Knoten gilt, sondern auch für die Summe aller Ströme, die aus einem ganzen Netz abfließen. Voraussetzung dafür ist, dass in diesem Netz für jeden Knoten und Schaltelement die Gl.(1) auch gilt. Ein Beispiel (Bild 2.) soll dies verdeutlichen:

Dargestellt ist ein Netz aus ohmschen Widerständen, das man auch als einen einzelnen Großknoten betrachten kann, aus dem die Ströme $I_{a},\quad I_{b},\quad I_{c}$ abfließen. Auch hier gilt:

$\sum I_{v}=I_{a}+I_{b}+I_{c}=0$

Gleichwohl erfüllen die Knoten A, B und C innerhalb des Netzes die Gl.(1)

Anmerkung: Die Angabe eines "negativen" Stromes bedeutet nur, dass die tatsächliche Stromrichtung dem Zählpfeil entgegengesetzt ist.

Die Maschenregel (2. Kirchhoffsche Gleichung)

Alle Teilspannungen eines Umlaufs bzw. einer Masche in einem elektrischen Netzwerk addieren sich zu Null. In einem Umlauf mit n Teilspannungen eines elektrischen Gleichstromnetzes gilt folgende Formel:

$\sum _{k=1}^{n}U_{k}=0$.

In Wechselstromnetzwerken muss die Summe der komplexen Effektivwerte oder komplexen Amplitude|Amplituden der Spannung betrachtet werden:

$\sum _{k=1}^{n}{\underline {U}}_{k}=0$.

Ein Netzwerk mit n unabhängigen Knotengleichungen hat n+1 unabhängige Maschengleichungen. Die Maschenregel ist ein Spezialfall des maxwellsche Gleichungen und darf nur bei Abwesenheit zeitlich ändernder Magnetfelder angewandt werden.

Spannungsteiler

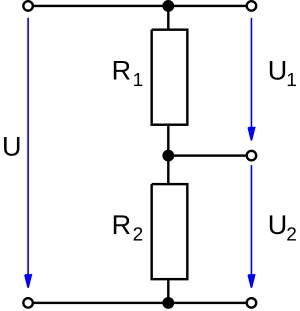
Allgemein

Der Spannungsteiler dient dazu, eine Spannung in kleinere Unterspannungen aufzuteilen. Die Aufteilung der Gesamtspannung erfolgt mit Hilfe von ohmschen Widerständen in Reihenschaltung, die als sogenannter Spannungsteiler arbeiten. Die beiden Widerstände können aber auch durch ein Potentiometer (Poti) realisiert werden, der Vorteil besteht darin, dass die Spannung an den Widerständen durch die Drehung des Potentiometers variabel einstellbar ist.

Unbelasteter Spannungsteiler

Formel:
$U_{2}={\frac {R_{2}}{R_{1}+R_{2}}}*U$

Merkregel:

$Teilspannung={\frac {Teilwiderstand}{Gesamtwiderstand}}*Gesamtspannung$

Merksatz:

Die Spannungen am Spannungsteiler verhalten sich so, wie die Widerstände an denen sie abfallen.

 ${\frac {U}{U_{2}}}={\frac {R_{1}+R_{2}}{R_{2}}}$

Belasteter Spannungsteiler

Erklärung: (sehr wichtig!)

Nach der Merkregel ergibt sich der Teilwiderstand als Parallelschaltung von R₂ und R_v. Als erstes müssen die beiden Widerstände R₂ und R_v zusammengefasst werden zu einem Ersatzwiderstand.

$R_{er}={\frac {R_{2}*R_{v}}{R_{2}+R_{v}}}\,$

Danach sieht die Schaltung genauso aus wie die eines unbelasteten Spannungsteilers, und man kann diese Formel verwenden. Anstatt des Widerstandes R₂ wird R_er eingesetzt (Formel: unbelasteter Spannungsteiler)!

Bei höherer Belastung (Widerstandswert von R_v wird kleiner) wird die Spannung U₂ an R₂ kleiner.

Anwendungsbeispiel

Ein Schalttafelinstrument hat einen Eingang 0...2 Volt. Es soll benutzt werden, um die Spannung eines 12 Volt Akku anzuzeigen. Wie wird der Spannungsteiler dimensioniert?

1. Wir legen fest, dass der Spannungsteiler 10 : 1 teilen soll, damit wird bei 12 Volt 1,2 Volt angezeigt.

2. Wir müssen den Eingangsstrom bzw. den Eingangswiderstand des Schalttafelinstruments kennen. (Es sei 10 M$\Omega$, 10 Megaohm).

3. Wir müssen die erforderliche Genauigkeit festlegen. 0,1 %

4. Aufgrund der Genauigkeit muss der Querstrom das 1000-fache des Laststromes sein.

Der Laststrom ist dann:

$I_{L}={\frac {U}{R}}={\frac {2\ V}{10\ {\frac {V}{\mu A}}}}\,$

$I_{L}=0,2\ \mu A\,$

Der Querstrom sei 1000 mal so hoch:

$I_{Q}=1000\cdot 0{,}2\ \mu A=200\ \mu A=0{,}2\ mA\,$

Am oberen Widerstand R₁ soll 18 V am unteren Widerstand R₂ soll 2 V abfallen.

$R_{1}={\frac {U_{1}}{I}}={\frac {18\ V}{0{,}2\ mA}}=90\ k\Omega \,$

$R_{2}={\frac {U_{2}}{I}}={\frac {2\ V}{0{,}2\ mA}}=10\ k\Omega \,$

Hinweis: Weil das Spannungsteilerverhältnis 10 : 1 ist, ist das Widerstandsverhältnis 9 : 1.

Hinweis: Wenn wir davon ausgehen, dass der Eingangswiderstand des Schalttafelinstruments genau ist, dann könnten wir dessen Widerstand bei R₂ berücksichtigen.

 

Stromteiler

Allgemein

Der Stromteiler teilt durch eine Parallelschaltung ohmscher Widerstände einen Strom in kleinere Teilströme auf. Der Stromteiler wird z.B. angewandt bei der Messung großer Ströme.

unbelasteter Stromteiler

Formel:
$I_{2}={\frac {R_{1}}{R_{1}+R_{2}}}\cdot I$

Merkregel:

$Teilstrom={\frac {Widerstand\ des\ anderen\ Teilstroms}{Ringwiderstand\ der\ Masche}}\cdot Gesamtstrom$

belasteter Stromteiler

Erklärung: Der Teilstrom durch einen Zweig ändert sich, wenn ein Zweig mit dem Widerstand R_v belastet wird. Für R₂ ist der Ersatzwiderstand R_er=R₂+R_v einzusetzen.

$I_{2}={\frac {R_{1}}{R_{1}+(R_{2}+R_{v})}}\cdot I$

 

Stern- und Dreieckschaltung

Dreieckschaltung

Links ist die Dreieckschaltung dargestellt. Die drei Widerstände $R_{1}$, $R_{2}$ und $R_{3}$ sind dabei beliebig und nicht unbedingt gleich groß.

Die Dreieckschaltung hat drei Anschlüsse, $A$ $B$ und $C$

Wenn $C$ offen ist, dann ist der Widerstand zwischen den Anschlüssen $A$ und $B$:

$R_{ABdo}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}+R_{3}}}}}$

Wenn zwischen $B$ und $C$ ein Kurzschluß ist, dann ist der Widerstand zwischen den Anschlüssen $A$ und $B$:

$R_{ABdk}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{3}}}}}$

Sternschaltung

Rechts ist die Sternschaltung dargestellt.

Die drei Widerstände $R_{4}$, $R_{5}$ und $R_{6}$ sind dabei beliebig und nicht unbedingt gleich groß.

Die Sternschaltung hat drei Anschlüsse, $A$, $B$ und $C$

Wenn $C$ offen ist, dann ist der Widerstand zwischen den Anschlüssen $A$ und $B$:

$R_{ABso}=R_{4}+R_{5}\,$

Wenn zwischen $B$ und $C$ ein Kurzschluß ist, dann ist der Widerstand zwischen den Anschlüssen $A$ und $B$:

$R_{ABsk}=R_{4}+{\frac {1}{{\frac {1}{R_{5}}}+{\frac {1}{R_{6}}}}}$

Gleichwertigkeit der Stern mit der Dreieckschaltung

Wenn die Widerstände in einem Kasten versteckt eingebaut sind, und der Kasten nur die Anschlüsse A, B und C hat, dann kann man durch Ausmessen der Widerstände R_AB , R_AC und R_BC ausrechnen, wie groß die Ersatzwiderstände R1, R2 und R3 einer Dreieckschaltung mit gleichen Messergebnis wären.

Oder man kann ausrechnen, wie groß die Ersatzwiderstände R4, R5 und R6 einer Sternschaltung mit gleichen Messergebnis wären.

Rechnerisch lässt sich eine Dreieckschaltung in eine Sternschaltung umrechnen und umgekehrt.

Das geschieht dadurch, dass man die Werte $R_{ABdo}$ mit $R_{ABso}$ gleichsetzt und $R_{ABdk}$ mit $R_{ABsk}$ gleichsetzt:

I $R_{ABdo}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}+R_{3}}}}}=R_{ABso}=R_{4}+R_{5}\,$

II $R_{ABdk}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{3}}}}}=R_{ABsk}=R_{4}+{\frac {1}{{\frac {1}{R_{5}}}+{\frac {1}{R_{6}}}}}$

Das Gleiche gilt für die Anschlüsse BC

Brückenschaltung

Das wird angewandt bei der Berechnung der Brückenschaltung. Um den Gesamtwiderstand ausrechnen zu können, kann man den rechten Teil R2 R4 R5 von einer Sternschaltung in eine Dreieckschaltung umwandeln. Danach zerfällt die Aufgabe in die bekannten Aufgaben Parallelschaltung und Reihenschaltung. Oder Man wandelt den oberen Teil von einer Dreieckschaltung aus R1, R2 und R5 in eine Sternschaltung um und rechnet dann weiter.

 

Die Spannungsquelle

Eine ideale Spannungsquelle ist ein Element, das unabhängig vom Strom und der angehängten Last eine konstante Spannung erzeugt.

Reale Spannungsquellen kann man sich vorstellen, als ideale Spannungsquelle, die die Leerlaufspannung $U_{0}$ liefert und einem, in Reihe geschalteten Widerstand $R_{i}$. Dieser wird "Innenwiderstand" der Spannungsquelle genannt.

Die Spannung an der realen Spannungsquelle ist von dem Strom abhängig, der entnommen wird.

$U_{a}=U_{0}-I*R_{i}$

Den Innenwiderstand kann man nicht direkt messen, sondern durch zwei Messungen bestimmen: eine ohne Last und noch einmal mit Last.

Beispiele für Spannungsquellen sind Batterien, Solarzellen und Generatoren. Die vier bekannten Batterietypen AAA, AA, C und D haben alle die gleiche Leerlaufspannung (1,5 V), aber unterschiedliche Innenwiderstände.

Auch elektrische oder elektronische Systeme können als Spannungsquellen betrachtet werden. So kann man z. B. eine Steckdose als Spannungsquelle betrachten, mit den Eigenschaften $U_{0}$ = 235 V und $R_{i}$ = 0,3 Ω

Daraus folgt, dass die Spannung an dieser Steckdose bei Entnahme von 10A auf 232 V absinkt.

Bei einem Kurzschluß würden dann 783,3 A Strom fließen - bis die Sicherung durchgeschmolzen ist.

Aufgaben

1. Eine Batterie hat im Leerlauf 1,5 Volt. Bei Belastung mit einem Glühbirnchen wird 1,32 V 0,38 A gemessen

Wie groß ist der Innenwiderstand der Batterie?

Wie groß ist der Kurzschlußstrom?

Annahme: Der Innenwiderstand sei von der Belastung unabhängig.

2. Eine Spannungsquelle liefert bei 10 A Belastung eine Spannung von 11,9 Volt. Bei 18 A Belastung eine Spannung von 11,72 Volt

Wie groß ist der Innenwiderstand der Spannungsquelle?

Wie groß ist die Leerlaufspannung?

Lösung: Siehe Ing:_GdE:_Die_Spannungsquelle_Loesungen

 

Zurück zum Inhaltsverzeichnis