Mathematikunterricht/ Sek/ Trigonometrie
Was ist Trigonometrie?
Trigonometrie behandelt die Definitionen und Beschreibung von Dreiecken. Die Trigonometrie beschreibt die entstehenden Figuren und Verhältnisse mit Hilfe von mathematischen Gleichungen zwischen einzelnen Elementen im Dreieck. Somit entstehen neue Definitionen und Objekte, die zur Konstruktion des einzelnen, bestimmten Dreiecks beitragen können.
Die Trigonometrie hat ihre Ursprünge in der Zeit der "griechischen Hochzeit", als neben Philosophie und Politik, die Geometrie und vor allem die Trigonometrie eine Hochphase hatte. Sie behandelt alles, was mit Dreiecken und darauf aufbauenden Figuren zu tun hat.
Benennung eines Dreiecks
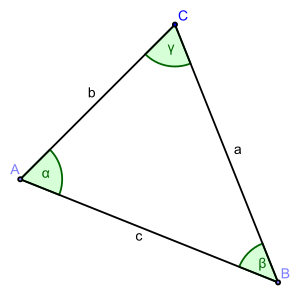
Bei der Benennung des Dreiecks hat sich folgender Standard durchgesetzt:
- Alle Seiten werden mit einem kleinen Buchstaben (a, b, c) benannt.
- Alle Ecken werden mit einem Großbuchstaben (A, B, C) benannt.
- Alle Winkel werden mit kleinen Griechischen Buchstaben (, und ) benannt.
- Der an einer Ecke anliegende Winkel wird wie die Ecke bezeichnet. (Der Winkel wird mit bezeichnet)
- Die einer Ecke gegenüberliegende Seite wird mit dem gleichen Buchstaben bezeichnet.
Wie auch sonst in der Mathematik üblich, werden die Ecken, Winkel und Seiten entgegen dem Uhrzeigersinn durchbuchstabiert:
Neben diesen Konventionen gibt es noch spezielle Regeln z.B. für das rechtwinklige Dreieck:
(Platzhalter: Rechtwinkliges Dreieck, Kathete, Hypotenuse, etc)
1. Die Höhen
Die Höhen eines Dreiecks sind das Lot auf eine Seite des Dreiecks vom gegenüberliegenden Punkt aus. Alle Höhen schneiden sich in einem Punkt . und bezeichnen die Höhen für die Seiten und .
2. Die Winkelhalbierenden
Eine Winkelhalbierende teilt einen Winkel in zwei gleich große Teile. Alle Winkelhalbierenden schneiden sich in dem Punkt . und bezeichnen die Winkelhalbierenden für die Winkel an den Punkten und .
3. Der Inkreismittelpunkt
Der Inkreis eines Dreiecks ist ein Kreis, der jede Seite des Dreiecks in genau einem Punkt berührt. Der Mittelpunkt des Inkreises ist der Schnittpunkt der Winkelhalbierenden . Der Radius des Kreises ist der minimale Abstand von dem Punkt zu einer Dreiecksseite.
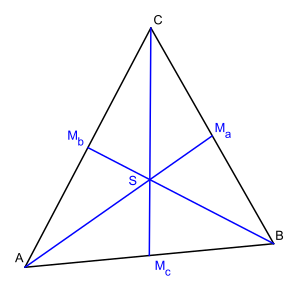
4. Die Seitenhalbierenden / Der Schwerpunkt
Die Seitenhalbierende eines Dreiecks wird die Strecke genannt, die einen Eckpunkt () des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Dreiecksseite verbindet. Die Seitenhalbierenden eines Dreiecks schneiden sich in dem Punkt , welcher 'Schwerpunkt' genannt wird. Der Schwerpunkt teilt die Seitenhalbierenden im Verhältnis .
5. Die Mittelsenkrechten
Eine Mittelsenkrechte steht senkrecht auf der Mitte einer Dreiecksseite. Alle Mittelsenkrechten schneiden sich im Punkt .
6. Der Umkreismittelpunkt
Der Umkreis ist der Kreis, der alle drei Eckpunkte des Dreiecks schneidet. Sein Mittelpunkt ist der Schnittpunkt der Mittelsenkrechten. Der Radius des Kreises ist die Länge der Strecke von Punkt zu oder . ()
7. Die Eulergerade
In jedem Dreieck liegen der Höhenschnittpunkt H, der Umkreismittelpunkt M und der Schwerpunkt S auf einer Geraden, die Eulergerade heißt. Die Strecke von H nach S ist doppelt so lang, wie die Strecke von S nach M.
Einen Sonderfall stellt das gleichseitige Dreieck dar. Dort fallen H, M und S auf einen Punkt, da Höhen, Mittelsenkrechten und Seitenhalbierende identisch sind.
(Sonder-)Formen von Dreiecken
Es gibt verschiedene Formen von Dreiecken die spezielle Namen tragen.
Das gleichschenklige Dreieck
Dieses Dreieck hat zwei gleichlange Seiten.  In diesem Dreieck gilt = .
In diesem Dreieck gilt = .
Das gleichseitige Dreieck
Beim gleichseitigen Dreieck haben alle Seiten die gleiche Länge.
 Alle Winkel sind 60° groß: = = = 60°
Alle Winkel sind 60° groß: = = = 60°
Das rechtwinklige Dreieck
Das rechtwinklige Dreieck besitzt einen Winkel mit 90°. Ausgehend von diesem Winkel werden die Seiten folgendermaßen benannt:
- Die den rechten Winkel einschließenden Seiten heißen Katheten
- Die dem rechten Winkel gegenüberliegende Seite wird Hypotenuse genannt.
- Außerdem kann man noch zwischen Ankathete und Gegenkathete unterscheiden. Diese werden immer in Bezug auf einen spitzen Winkel so genannt. Die am spitzen Winkel anliegende Kathete nennt man Ankathete, die dem spitzen Winkel gegenüberliegende Gegenkathete (evtl. Merksatz hinzufügen)
(Hier Bild mit den Benennungen einfügen (evtl. 2 wg. An- u. Gegenkathete))
Dieses Wissen braucht man vor allem später für die Winkelfunktionen
Verhältnisse im rechtwinkligen Dreieck
Kathetensätze
Bei den Kathetensätzen geht es darum, Verhältnisse zwischen den Seiten eines rechtwinkligen Dreiecks zu finden.

Kathetensatz (Euklid)
- Beweis:
- 1. Nachweis mittels ähnlichen Dreiecken:
- Im oben abgebildeten Dreieck sind drei ähnliche Dreiecke vorhanden.
- Die Ähnlichkeit wird mit Hilfe einer der vier Ähnlichkeitsätze nachgewiesen: "Zwei Dreiecke sind genau dann ähnlich, wenn sie in zwei Winkeln übereinstimmen"
- Folgende Winkel tauchen wiederholt auf:
- 2. Verwendung von Streckenverhältnissen
Analog
Das Quadrat einer Kathete ist gleich dem Produkt des anliegenden Hypotenusenabschnitts und der Hypotenuse.
Innenwinkel
Winkelfunktionen

Für die Bearbeitung dieses Kapitels muss man zunächst wissen, was eine (An-)Kathete, Gegenkathete und eine Hypotenuse ist (siehe rechtwinkliges Dreieck). Vor allem in der Physik braucht man die Winkelfunktionen häufig.
Merkhilfe
Bewährt als Merkhilfe für die Berechnung hat sich folgende Eselsbrücke:
(sprich: gaga HühnerHof AG)
.....G....A...G...A
.....H....H...A...G
....sin..cos.tan.cot
mit G= Gegenkathete, A= Ankathete, H= Hypotenuse
Sinus
Der Sinus ist ein Seitenverhältnis. Er bestimmt das Verhältnis der Gegenkathete (von ) zur Hypotenuse. Abgekürzt:
Cosinus
Der Cosinus ist Ankathete durch die Hypotenuse. Im Bild oben:
Ankathete (von ) zur Hypotenuse. Abgekürzt:
Im Bild oben:
Tangens
Der Tangens von (von )
Gegenkathete (von ) zur Ankathete. Abgekürzt:
Des Weiteren ist der Tangens als der Quotient von Sinus und Cosinus definiert:
Cotangens
Der Cotangens von ist definiert als das Verhältnis der Ankathete (von ) zur Gegenkathete. Abgekürzt:
Analog zum Tangens gilt hier, dass der Cotangens das Verhältnis von Cosinus zu Sinus ist.
Secans
Der Secans von ist definiert als der Quotient von der Hypotenuse durch die Ankathete (von ). Abgekürzt:
(Im deutschen Sprachraum wird der Secans nur selten verwendet.)
Cosecans
Der Cosecans von ist definiert als der Quotient von der Hypotenuse durch die Gegenkathete (von ). Abgekürzt:
(Im deutschen Sprachraum wird der Cosecans nur selten verwendet.)
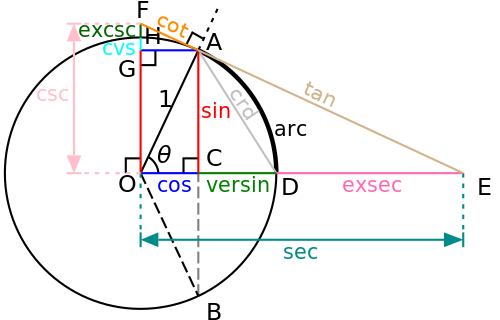
Einheitskreis (r = 1)
Diese 4 Winkelfunktionen lassen sich am besten am Einheitskreis veranschaulichen. ( α=Θ )
Sinus- und Kosinussatz
Der Sinus, Kosinus und Tangens kann nur in einem rechtwinkligen Dreieck verwendet werden. Mithilfe von Sinus- und Kosinussatz kann man jedes Dreieck berechnen solange genügend Werte vorhanden sind, denn jedes Dreieck kann in zwei kleine rechtwinkelige Dreiecke zerlegt werden.
Sinussatz

Mithilfe des Sinus kann man nun beide kleine Dreiecke nach auflösen:
nun setzt man beide Gleichungen nach gleich:
nun kann die Gleichung noch durch und dividieren und man erhält:
Dies kann man für jeden Winkel und jede Seite machen:
Kosinussatz
...
Klärung von Fachbegriffen/Zeichen
- Kathete
- Seite eines rechtwinkeligen Dreiecks, die am rechten Winkel liegt.
- Hypotenuse
- Die längste Seite im rechtwinkligen Dreieck; sie liegt dem rechten Winkel gegenüber.
- Ankathete
- Die Kathete am gegebenen Winkel.
- Gegenkathete
- Die Kathete gegenüber dem gegebenen Winkel.
- Winkel
- Geometrische Figur, welche aus zwei Strahlen, die von einem gemeinsamen Punkt ausgehen, und der dazwischen liegenden Fläche besteht.

- spitzer Winkel
- Winkel kleiner als 90°.
- rechter Winkel
- Winkel mit genau 90°.
- stumpfer Winkel
- Ein Winkel größer als 90° und kleiner als 180°.
- gestreckter Winkel
- Ein Winkel der Größe 180°.
- überstumpfer (erhabener) Winkel
- Ein Winkel größer als 180° und kleiner als 360°.
- Vollwinkel
- Ein Winkel, der 360° groß ist.
- Komplementärwinkel
- Bezeichnet einen Winkel, der den gegebenen Winkel zu 90° erweitert.
- Supplementärwinkel
- Ein Winkel, der den gegebenen Winkel zu 180° erweitert.
- Winkelhalbierende
- Eine Gerade, die durch den Schnittpunkt von zwei weiteren Geraden verläuft, und zu beiden den gleichen Winkel hat.
- Seitenhalbierende
- Eine Gerade, die durch die Mitte einer Strecke verläuft.
- Mittelsenkrechte
- Eine Seitenhalbierende, die die Strecke unter 90° schneidet.