Astronomische Berechnungen für Amateure/ Druckversion/ Astronomische Distanzen
Erdnaher Raum[Bearbeiten]
Distanzbestimmungen gehören in der Astronomie zu den schwierigen Aufgaben. Es ist auch bezeichnend, dass man von „Bestimmung“ und nicht von „Messung“ spricht. Als zweite Erschwernis kommt hinzu, dass die Zahlenwerte rasch unvorstellbar groß werden. Die „astronomischen Werte“ sind ein stehender Begriff unserer Sprache. Der erdnahe Raum ist ein Bereich, wo die Werte noch vorstellbare Grössenordnungen haben. Wo dieser erdnahe Raum beginnt und wo er endet ,ist eine Definitionsfrage. Wir wollen recht pragmatisch von bis ca. 10 Million Kilometer Abstand von der Erde ausgehen. Wie schon diese Festlegung zeigt, verwenden wir in diesem Bereich des Kosmos die aus dem Alltag bekannten Längeneinheiten.
In diesem Teil des Weltalls interessieren vor allem die folgenden Objekte:
- Meteore und Feuerkugeln, die in den obersten Schichten der Atmosphäre Leuchterscheinungen hervorrufen.
- Künstliche Satelliten, die die Erde umkreisen, wie z. B. die internationale Raumstation ISS oder die GPS-Satelliten, um zwei Beispiele zu nennen.
- Die erdnahen Objekte (Near Earth Objects NEO) oder präziser die erdnahen Asteroiden NEA, die im schlimmsten Fall sogar mit der Erde kollidieren können.
- Nicht zu vergessen: Unser Mond bewegt sich in diesem Bereich.
Für unser Thema Berechnungen sind die folgenden Fragen von Interesse:
- Höhenbestimmungen – dazu benötigt man Methoden der Sphärischen Astronomie, auf die wir im folgenden Kapitel eingehen werden
- Bahnbestimmungen – ein Thema für die Himmelsmechanik im übernächsten Kapitel
- Bestimmung der täglichen Parallaxe
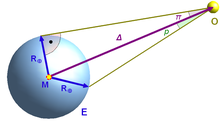
Mit dem Begriff tägliche Parallaxe bezeichnen wir folgendes Phänomen: Auf die Erde bezogene Angaben verwenden den Erdmittelpunkt als Referenz („geozentrische Position“). Gerade für Objekte im erdnahen Raum kann aber auch bei nicht sehr genauen Rechnungen nicht vernachlässigt werden, dass der Beobachter nicht im Erdmittelpunkt, sondern auf der Erdoberfläche sitzt („topozentrische Position“) und somit ein Richtungsunterschied zu einem (fiktiven) Beobachter im Erdzentrum besteht. Diesen Unterschied nennt man die tägliche Parallaxe. Hat der betrachtete Himmelskörper vom Erdmittelpunkt den geozentrischen Abstand Δ (in km) und beträgt der Erdradius , dann berechnet sich der Parallaxenwinkel π wie folgt:
Dies ist die grösstmögliche Verschiebung eines Himmelskörpers vor dem Sternenhintergrund. Sie wird auch als Äquatorial-Horizontalparallaxe bezeichnet. Wie gross die wirkliche Parallaxe p ist, werden Sie sehen, wenn im nächsten Kapitel die Koordinatensysteme behandelt werden.
Die Entfernung bestimmt zusammen mit dem wahren Radius auch den scheinbaren Radius bzw. den scheinbaren Durchmesser eines Objektes am Erdhimmel. Wenn wiederum Δ der geozentrische Abstand des Himmelskörpers und R sein Radius ist (beide in km), s der scheinbare Radius bzw. D der scheinbare Durchmesser des Himmelskörpers am Erdhimmel (beide in ° oder '), so lautet der Zusammenhang:
Übungen
- Wie gross ist die Horizontalparallaxe des Mondes in seiner durchschnittlichen Entfernung von 384 400 km, in seiner Perigäumstellung von 356 400 km und in der Apogäumstellung von 406 700 km?
- Wie gross ist die Horizontalparallaxe eines Himmelskörpers, der sich an der Grenze des von uns als „erdnahen Raum“ bezeichneten Gebietes bewegt?
- Wie müssen Erde, Beobachter und Himmelskörper zueinander stehen, dass der Beobachter keine parallaktische Verschiebung des Himmelskörpers feststellen kann? Wie müssen sie zueinander stehen, damit gerade die Horizontalparallaxe (also die grösstmögliche parallaktische Verschiebung) beobachtet werden kann?
- Nehmen Sie das Beispiel Mond: Welche anschauliche Bedeutung hat die auf der Erde gemessene Horizontalparallaxe für einen Beobachter auf dem Mond (z. B. für einen Astronauten)?
- Welchen scheinbaren Radius bzw. Durchmesser hat der Mond (R = 1738 km) in mittlerer, erdnaher und erdferner Position?
- In welcher Position ist der scheinbare Durchmesser des Mondes grösser: Wenn er am Horizont steht oder wenn er im Zenit steht?
Sonnensystem[Bearbeiten]
Im Sonnensystem werden die Distanzen zwar gelegentlich noch in Kilometern angegeben, doch weitaus häufiger wird mit der Astronomischen Einheit AE gerechnet. Dies aus zwei Gründen:
- Die Zahlenwerte sind „handlicher“. So wie man im Alltag grosse Strecken auch nicht in mm angibt, weil die Zahlenwerte gross und damit unvorstellbar werden, so zieht man es vor, die Distanzen im Sonnensystem in AE anzugeben.
Beispiel:
Die grosse Bahnhalbachse der Jupiterbahn beträgt 5.20 AE oder 778 Millionen km (gerundete Werte). Mit der Angabe 5.20 AE weiss man, dass diese Bahn gut 5-mal grösser ist als die Erdbahn – man hat eine Ahnung von den relativen Grössenordnungen. Die Angabe 778 Millionen km ist eine rein rechnerische Grösse, wir können uns darunter nichts mehr vorstellen.
- Bis gegen 1900 war es ausserordentlich schwierig, die exakten Abmessungen der Bahnen im Sonnensystem (und damit die relevanten Distanzen) mit einer genügenden Genauigkeit zu bestimmen.
Um dieses Argument zu verstehen, überlege man: bis weit ins 20. Jahrhundert war die Triangulation – also eigentlich die Messung der Parallaxe eines Himmelskörpers – die einzige Möglichkeit, im Sonnensystem Distanzen messen zu können. Die Horizontalparallaxe der Sonne beträgt π = 0.00244° = 8.794". Weil aber die Sonne alle Sterne überstrahlt, lässt sich diese Verschiebung vor dem Sternenhintergrund nur über indirekte Methoden bestimmen.
Will man mit der Triangulation die Distanz Erde – Sonne auf 1 km genau bestimmen, benötigt man eine Genauigkeit der Winkelmessung von
Umgekehrt erzielt man mit einer Messgenauigkeit von z.B. 0.5" nur eine Genauigkeit von etwa 360 km. Man konzentrierte sich darum auf die Messung des Abstandes Erde – Venus, denn im 19. Jahrhundert kannte man keinen anderen Körper im Sonnenystem, der der Erde näher kam: bei einem Transit vor der Sonnenscheibe beträgt ihr Abstand zur Erde „nur“ ca. 42 Millionen km. Das ergibt eine Horizontalparallaxe von 0.0087° oder 31.3". Für die Belange der Astronomen war das zwar die beste Möglichkeit, aber man hätte sich eine noch genauere Bestimmung der AE gewünscht. Dies wurde möglich, als 1898 der Asteroid Eros entdeckt wurde, der der Erde regelmässig bis 20 Millionen km (entspricht einer Horizontalparallaxe von 0.0183° = 65.8" – also mehr als 1') nahe kommt. Später wurden weitere Asteroiden entdeckt, die der Erde noch näher kommen, teilweise bis in den erdnahen Raum (Definition gemäss vorangehendem Kapitel). Einerseits die kürzeren Distanzen, die ausgemessen werden mussten und damit zu grösseren Parallaxen führten, andererseits die scheinbare Grösse des Objektes, dessen Position vor dem Sternenhintergrund bestimmt werden musste, waren entscheidend für die Verbesserung der Genauigkeit: ein feines Lichtpünktchen eines kleinen Asteroiden kann genauer lokalisiert werden als das verhältnismässig grosse Scheibchen eines Planeten wie Venus.
In der 2 Hälfte des 20. Jahrhunderts trat an die Stelle der Triangulation zunehmend die direkte Messung der Laufzeit von Radarstrahlen, die von Venus reflektiert werden. Damit erreichte man erst jene Genauigkeit der Distanzbestimmung, die für die Raumfahrt unerlässlich ist. Der heute gültige Wert für die AE hat eine Genauigkeit von ca. 1 km.
Die Parallaxe ist bei exakten Rechnungen (z.B. genaue Ephemeriden) grundsätzlich auch für die Objekte des Sonnensystems zu berücksichtigen. Dabei wird selten die Parallaxe direkt nach den Formeln des voranstehenden Kapitels berechnet, sondern über die Sonnenparallaxe wie folgt:
Da wir es im Sonnensystem immer mit sehr kleinen Parallaxenwinkeln zu tun haben, dürfen wir von der für solche Winkel gültigen Beziehung sin π ≈ π (Winkel im Bogenmass!) Gebrauch machen. Dies führt zur Beziehung für die Parallaxe (in Bogensekunden) eines Objektes im Sonnensystem, wie sie meistens verwendet wird ( in AE):
Ein zweiter Effekt kann im Sonnensystem nicht mehr vernachlässigt werden: die Lichtzeit. Damit wird folgender Effekt bezeichnet: weil sich das Licht nicht unendlich schnell, sondern mit einer zwar sehr grossen, aber endlichen Geschwindigkeit ausbreitet, sehen wir einen Himmelskörper nie dort, wo er zum Beobachtungszeitpunkt t steht, sondern dort, wo er zum Zeitpunkt t – τ gestanden hat. Zu diesem Zeitpunkt wurde das Licht ausgesendet, das den Beobachter zum Zeitpunkt t erreicht. Die Lichtzeit τ ist diejenige Zeit, die das Licht bei einer Geschwindigkeit von c = 299 792 458 m/s (knapp 300 000 km/s) benötigt, um die Strecke Δ vom Himmelskörper bis zur Erde zurück zu legen. Es gilt
Man erkennt daraus: ist Δ = 1 AE – entspricht die Entfernung also gerade etwa dem mittleren Abstand der Sonne zur Erde –, dann ist τ = 499 s bzw. 0.005776 d bzw. 8 m 19 s. So lange braucht das Licht von der Sonne zur Erde. Bei genauen Ephemeridenberechnungen von Himmelskörpern des Sonnensystems sind die Positionen für einen Zeitpunkt zu berechnen, der τ Tage vor dem Beobachtungszeitpunkt liegt. Da man τ und Δ zum voraus nicht kennt, ist diese Aufgabe nur iterativ zu lösen: zunächst berechnet man die Position zum Zeitpunkt t und gewinnt eine erste Schätzung Δ1 und damit auch τ1. Nun wiederholt man die Rechnung für den Zeitpunkt t – τ1 und prüft, ob Δ2 (der neu errechnete Abstand) sich so sehr verändert hat, dass ein wesentlich anderer Wert für τ2 resultiert. In diesem Fall muss die Rechnung nochmal für den neuen Zeitpunkt t – τ2 wiederholt werden.

Abstand – und damit eigentlich die Parallaxe – und Lichtzeit sind miteinander verknüpft. Im 17. Jahrhundert war es der dänische Astronom Ole Roemer (1644 – 1710), der dies feststellte, und der diesen Zusammenhang nutzte, um zum ersten Mal den Wert der Lichtgeschwindigkeit zu bestimmen . Der Sachverhalt:
Im 17. Jahrhundert verfügte man noch nicht über genügend genau gehende Uhren, um über weite Strecken beispielsweise auf hoher See eine genaue Bestimmung der eigenen Position, vor allem der geografischen Länge, zu ermöglichen. Doch – so glaubte man – die Natur stellt eine Zeitmarke zur Verfügung, an der man immer wieder die eigenen ungenau gehenden Uhren eichen kann: den Jupitermond Io, der den Planeten in nicht ganz 2 Tagen einmal umrundet. Dabei tritt er regelmässig in den Planetenschatten. Der Schatteneintritt bzw. der Schattenaustritt kann recht genau beobachtet werden. Bereits Galilei hatte vorgeschlagen, diese Ereignisse als Marken zur Eichung von Uhren zu verwenden. Doch bald stellte man systematische Abweichungen von den vorausberechneten und in Tabellen veröffentlichten Zeiten fest: mal trat das Ereignis verfrüht ein, mal verspätet. 1676 stellte Ole Roemer fest, dass die Abweichungen mit den relativen Stellungen von Erde und Jupiter zusammenhingen. Er interpretierte sie darum als Lichtzeit. Damit gelang es zum ersten Mal, die Lichtgeschwindigkeit zu messen. Bis zu diesem Zeitpunkt war nicht klar, ob das Licht eine endliche oder eine unendliche Ausbreitungsgeschwindigkeit habe. Erst 1834 wurde zum ersten Mal die Lichtgeschwindigkeit auf der Erde gemessen, ab ca. 1850 waren die Messmethoden so weit verfeinert, dass sie (aus heutiger Sicht) gute Resultate lieferten.
Übungen:
- Berechnen Sie die Horizontalparallaxe der Planeten Merkur bis Pluto für den erdnächsten bzw. erdfernsten Punkt der Bahn. Nehmen Sie zur Vereinfachung an, bei den Planetenbahnen handle es sich um Kreisbahnen mit der Sonne im Mittelpunkt.
- Welchen scheinbaren Durchmesser hat das Venusscheibchen in der erdnächsten Stellung des Planeten? Welchen scheinbaren Durchmesser errechnen Sie für Eros? Die Daten: Venus DV = 12 100 km, ΔV = 42 Mio km; Eros: De1 = 13 km, De2 = 33 km (Eros hat eine längliche Gestalt von ca. 13 × 13 × 33 km), Δe = 20 Mio km. Runden Sie das Ergebnis!
- Berechnen Sie die Lichtzeit für die Planeten Merkur bis Pluto jeweils in der erdnächsten und in der erdfernsten Stellung. Nehmen Sie wieder vereinfachend an, bei den Planetenbahnen handle es sich um Kreisbahnen mit der Sonne im Mittelpunkt.
- In welcher Stellung stehen Jupiter und Erde zueinander, wenn die Verfinsterungen am meisten verfrüht sind, in welcher Stellung sind sie am meisten verspätet? Wieviel macht der Effekt gegenüber einer mittleren Zeit aus, und in welcher Stellung stehen Erde und Jupiter zu diesem Zeitpunkt? Können Schatteneintritt (Verfinsterung von Io) und Schattenaustritt beim gleichen Umlauf beobachtet werden? Nehmen Sie zur Vereinfachung für alle drei Bahnen Kreisform an: Erde rE = 1 AE; Jupiter rJ = 5.20 AE; Io rI = 422 000 km.
Kosmos[Bearbeiten]
Die äussere Grenze des Sonnensystems wird von der sog. Oort'schen Wolke gebildet, aus der die langperiodischen Kometen stammen. Der Ausdruck „äussere Grenze“ besagt, dass die Sonne diese Objekte durch ihre Anziehungskraft noch an sich zu binden vermag. Bei Objekten, die noch weiter entfernt sind, ist dies nicht mehr der Fall ist. Diese Grenze liegt bei ca. 100 000 AE. Ausserhalb beginnt der interstellare Raum unserer Galaxis, und noch weiter draussen liegt der intergalaktische Raum. In diesem Bereich führen Distanzangaben in der Einheit AE schnell zu grossen Zahlenwerten. Für diesen Bereich sind darum neue Distanzeinheiten gesucht.
Viele Amateure benutzen in diesem Bereich das Lichtjahr – abgekürzt LJ oder ly – als Entfernungsmass. Es ist jene Strecke, die das Licht mit einer Geschwindigkeit von knapp 300 000 km/s in einem Jahr zurücklegt. In Kilometern ausgedrückt sind das 9.460 54 ∙ 1012 km oder 63 200 AE. Die Oort'sche Wolke hat ihre äussere Grenze also bei rund 1.5 Lichtjahren. Anders gesagt: wenn wir einen Kometen in der Oort'schen Wolke beobachten könnten, würden wir ihn an dem Ort und in dem Zustand sehen, wo und wie er vor 1½ Jahren war. Unsere eigene Galaxis hat einen Durchmesser von rund 100 000 Lichtjahren, das Sonnensystem befindet sich zwischen 25 000 und knapp 30 000 Lichtjahre vom galaktischen Zentrum entfernt. Die nächste grosse Galaxie, der Andromedanebel M31, befindet sich in einer Entfernung von 2.4 bis 2.9 Millionen Lichtjahren. An diesen Angaben sehen wir ein Grundproblem der Distanzbestimmung im Kosmos: die Distanzen sind mit grossen Unsicherheiten behaftet – umso grösser, je weiter entfernt ein Objekt ist. Es fehlt eben die Möglichkeit, ein Messband auszulegen.
Astronomen ziehen als Entfernungsmass das Parsec – abgekürzt pc – vor: es ist jene Distanz, aus der der Radius der Erdbahn (1 AE) unter einem Winkel von 1" gesehen werden könnte. Oder anders ausgedrückt: ein (hypothetisches) Objekt in dieser Entfernung hätte bezogen auf die Erdbahn eine Parallaxe von 1" (jährliche Parallaxe). Es gilt:
Ein Parsec ist das Äquivalent von 206 260 AE oder 3.261 56 Lichtjahren. In unserer Galaxis werden die Distanzen in kpc = 1000 pc gemessen, ausserhalb in Mpc = 1 000 000 pc.
Der nächste Fixstern Proxima Centauri ist vom Sonnensystem 4.22 ly oder 1.295 pc entfernt. Es handelt sich um einen roten Zwergstern der scheinbaren Helligkeit 11.05m. Vermutlich gehört er zum Mehrfachsystem α Cen im Sternbild des Zentauren. Die Distanz besagt umgekehrt, dass die jährliche Parallaxe von Proxima Centauri 0.772" beträgt. So klein dieser Wert ist, so ist er doch messbar und damit Grundlage der Entfernungsbestimmung. Dies ist allerdings nur mit den nächsten Fixsternen möglich. Im übrigen sind weder α Cen noch Proxima Centauri von Mitteleuropa aus sichtbar.
Der Zusammenhang zwischen der jährlichen Parallaxe π eines Fixsterns und seiner Entfernung Δ in pc ist einfach: wegen sin π ≈ π für kleine Winkel π (was für Fixsternparallaxen immer erfüllt ist) gilt:
Die jährliche Parallaxe ist das Abbild der Bewegung der Erde um die Sonne. Als Folge beschreiben die nächsten Sterne eine kleine Ellipse an der unendlich weit entfernten Himmelskugel. Es ist sozusagen das Pendant der Planetenschleifen im Sonnensystem. 1838 gelang es erstmals dem deutschen Astronomen Friedrich Wilhelm Bessel, beim Stern 61 Cyg (im Sternbild Schwan) die Parallaxe zu messen – 0.3" war das Ergebnis.
Die Fixsternparallaxen sind zu unterscheiden von ihrer Eigenbewegung. Darunter ist folgendes zu verstehen: trotz ihres Namens sind Fixsterne nicht wirklich fix, nur bewegen sie sich sehr langsam vor dem Hintergrund der Himmelskugel. Es handelt sich dabei um die Bewegung um das Zentrum der Galaxis. Unser Sonnensystem braucht für einen Umlauf bei einer Geschwindigkeit von 250 km/s mehr als 210 Millionen Jahre. Die Bewegung eines jeden Sterns kann in zwei Komponenten zerlegt werden: die eine Komponente zeigt in Richtung der Verbindungsstrecke Sonnensystem – Stern und gibt an, wie schnell sich der Stern von uns wegbewegt oder auf uns zubewegt. Diese Komponente kann direkt aus dem Spektrum abgeleitet werden, denn sie bewirkt eine geschwindigkeitsabhängige Verschiebung der Spektrallinien zu grösseren Wellenlängen, wenn sich der Stern von uns entfernt („Rotverschiebung“) bzw. zu kürzeren Wellenlängen, wenn er sich uns nähert. Die zweite Komponente steht senkrecht dazu und gibt an, in welcher Richtung und mit welchem Betrag sich die Position des Sterns an der Himmelskugel verändert. Jedoch sind diese Beträge so klein, dass sich erst im Laufe von Jahrtausenden Veränderungen am Himmel ergeben, die schon dem blossen Auge auffallen. Für genaue Rechnungen sind sie aber selbst für kurze Zeitabstände zu berücksichtigen. Dies gilt z.B., wenn Sternpositionen eines Katalogs von der einen Standardepoche auf eine andere umgerechnet werden sollen. Der Stern mit der grössten Eigenbewegung, die bis heute gemessen wurde, ist Barnards Pfeilstern. Mit 10.34" pro Jahr verschiebt er sich so schnell wie kein anderer vor der Himmelskugel. Es handelt sich um einen roten Zwerg der scheinbaren Helligkeit 9.5m im Sternbild Ophiuchus (Schlangenträger). Als viertnächster Stern finden wir ihn in einer Entfernung von 1.84 pc (5.98 ly).

Noch einen anderen Hintergrund hat die Aberration, denn die Ursache ist die Bewegung der Erde um die Sonne (jährliche Aberration) bzw. die Rotation der Erde (tägliche Aberration). Die Erklärung des Effektes (s. nebenstehende Grafik): trifft das einfallende Licht eines entfernten Sternes auf die Öffnung eines Teleskops, so bewegt sich das Instrument weiter, während das Licht durch den Fernrohrtubus läuft. Damit es auch wirklich in der Tubusachse bleibt und das Okular erreicht, muss das Fernrohr leicht in Bewegungsrichtung geneigt werden. Die Aberrationskonstante für die jährliche Aberration – dh. der maximale Winkel, um den man das Teleskop neigen muss – beträgt 20.495 52". Die Konstante für die tägliche Aberration beträgt nur 0.32", so dass dieser Effekt in der Regel vernachlässigt werden kann. Als Folge der Aberration beschreiben alle Sterne (unabhängig von ihrer Entfernung) eine Ellipse auf der unendlich weit entfernten Himmelskugel, deren grosse Halbachse 20.5" (jährliche Aberration) bzw. 0.32" (tägliche Aberration) misst. Der Effekt wurde 1725 vom englischen Astronomen James Bradley entdeckt, der aber eigentlich die Parallaxe messen wollte.
Theoretisch gibt es noch die nichtperiodische säkulare Aberration. Sie rührt von der Relativbewegung des Sonnensystems gegenüber seiner Umgebung her. In der Praxis kann sie aber vernachlässigt werden.
Übungen
- Wie gross ist die jährliche Parallaxe für den äussersten Planeten Neptun? Wie gross für Pluto?
- Wie gross ist die Geschwindigkeit von Barnards Pfeilstern in tangentialer Richtung in km/s?
- Verifizieren Sie die Konstante der täglichen Aberration!
- Im Wikipedia-Artikel über die Aberration steht über Bradleys Entdeckung: „Bradley war jedoch imstande, die scheinbaren Ortsveränderungen – welche quer zu seiner Erwartung verliefen – richtig zu deuten.“ In einem im Internet zugänglichen Lehrtext der Uni Freiburg[1] steht: „Die Bewegung der Erde um die Sonne ruft eine jährliche Aberration der Sterne im geozentrischen System hervor ähnlich der jährlichen Parallaxe, allerdings mit einer Phasenverschiebung um 90°.“ Was meinen die beiden fett hervorgehobenen Textteile?
- Angenommen, das menschliche Auge könnte die 20.5" der jährlichen Aberration auflösen: wäre sie dann auch von blossem Auge festzustellen, oder ist es nur ein Teleskop-Phänomen?
Nachweis:
Erdglobus[Bearbeiten]
Die Erde als Kugel[Bearbeiten]
Für einfache, wenig genaue Rechnungen kann man die Erde als eine Kugel betrachten. Jeder Ort auf der Erdoberfläche lässt sich durch die Angabe von drei Koordinatenwerten eindeutig bestimmen: die (geografische) Länge λ, vom Meridian durch Greenwich als Nulllinie (0°) nach Osten und nach Westen je bis 180° gezählt (oft nach Osten positiv, nach Westen negativ) und die (geografische) Breite φ, nach Norden bis zum Nordpol positiv bis +90°, nach Süden bis zum Südpol negativ bis –90° gezählt. Als dritte Koordinate kommt die Höhe über der Kugeloberfläche hinzu. Gewöhnlich wird von der Höhe über Meer (ü.M.) oder über Normalnull gesprochen.
Die Erde als Rotationsellipsoid[Bearbeiten]
Steigen die Ansprüche an die Genauigkeit, muss die Abweichung der Erdoberfläche von der Kugelgestalt berücksichtigt werden. In den allermeisten Fällen genügt es für die Ansprüche von Amateuren, die Erde als Rotationsellipsoid zu betrachten. Ein Rotationsellipsoid als Drehkörper entsteht, wenn eine Ellipse mit grosser Halbachse a und kleiner Halbachse b um letztere als Drehachse rotiert. M.a.W.: ein Querschnitt durch die beiden Pole ergibt eine Ellipse, ein Schnitt senkrecht zur Achse einen Kreis als Schnittfläche. Die beiden in der Äquatorebene gelegenen Achsen des Rotationsellipsoids sind gleich gross und gleich dem Äquatorradius der Erde a = 6378.137 000 km[1]. Die dritte, zu den Polen weisende Achse ist dagegen verkürzt. Sie ist gleich dem Polradius der Erde b = 6356.752 314 km. Das Verhältnis
heisst Abplattung. Die Zahlenwerte beziehen sich auf das Erd-Ellipsoid WGS 84, das zB. den GPS-Koordinaten zugrunde liegt[2]. Die numerische Exzentrizität ε eines Erdmeridians ist gegeben durch
und .

Zur Illustration dient die nebenstehende Grafik. Wie im Falle der Kugel werden die geografischen Koordinaten definiert: die geografische Länge λ ist der Winkel zwischen der Richtung zum Meridian NGA2S durch den Referenzort Greenwich G und zum Meridian NPA3S durch den betrachteten Ort P, gemessen in der Äquatorebene mit dem Erdmittelpunkt als Scheitel. Die Vorzeichenkonventionen sind die gleichen wie auf der Kugel. Für die Festlegung der geografischen Breite φ gehen wir von folgender Betrachtung aus. nPs ist die Horizontebene eines Beobachters im Punkt P auf der Erdoberfläche, Z seine Zenitrichtung. PN' verläuft parallel zur Erdachse und weist zum Himmelsnordpol. Verlängert man ZP ins Erdinnere, so trifft die Verlängerung in der Regel nicht den Erdmittelpunkt M, sondern schneidet den Äquatordurchmesser bei Q. Die Strecke MQ kann bis zu 20 km betragen. A3QP oder, was das gleiche ist, nPN' ist die geografische Breite. Als dritte Grösse kommt noch die Höhe H über dem Ellipsoid hinzu, gemessen auf der Geraden PZ.
Wird die Breite φ' dagegen vom Erdmittelpunkt aus gemessen (sog. geozentrische Breite), so resultiert ein etwas kleinerer Wert. Nur am Äquator und an den Polen stimmen die beiden Werte überein. Für einen Ort auf der Oberfläche des Ellipsoids gilt:
Die Strecke ρ = MP ist der Abstand des Punktes P vom Erdmittelpunkt M. Im allgemeinen befindet sich der Beobachter in der Höhe H über dem Ellipsoid. Berechnen wir tägliche Parallaxen, Finsternisse oder Bedeckungen, dann benötigen wir die Grössen ρ ∙ sin ϕ' und ρ ∙ cos ϕ'. Über die Hilfsgrösse u berechnen wir diese Ausdrücke mit folgenden Formeln:
Entsprechend dem Vorzeichen von ϕ bzw. ϕ' ist ρ ∙ sin ϕ' > 0 auf der nördlichen Hemisphäre und ρ ∙ sin ϕ' < 0 auf der südlichen Hemisphäre. ρ ∙ cos ϕ' > 0 gilt für alle Breiten. ρ ist der Abstand des Beobachters in P vom Erdmittelpunkt, und zwar in Einheiten des Äquatorradius a.
Kennen wir von einem Punkt auf dem Ellipsoid die geografische Breite ϕ, so lässt sich die Differenz ϕ – ϕ' mittels der folgenden Formel berechnen:
Wenn die Hilfsgrösse |u| = 45° erreicht, dann hat diese Differenz ihren grössten Wert. Bezeichnen wir in diesem Fall die zugehörige geographische Breite mit ϕ0 bzw. die geozentrische Breite mit ϕ'0, so gilt:
Damit finden wir , den gleichen Wert, den wir auch mit der voran stehenden allgemeinen Formel für die Differenz finden.
Für einen Ort auf der Oberfläche des Rotationsellipsoids kann die Entfernung ρ mit folgender Formel berechnet werden:
Die Winkelgeschwindigkeit der Erde bei ihrer Drehung um die eigene Drehachse beträgt ω = 7.292 115 07 ∙ 10–5 rad/sec. Genauer gesagt müsste man sagen: ω hatte zum Zeitpunkt 2000.0 diesen Wert (was einer siderischen Tageslänge von 86 164.100 s entspricht), denn die Rotationsdauer nimmt ja ab und ist gleichzeitig noch unregelmässigen Schwankungen unterworfen.
Ein Breitenkreis in der Breite φ hat den Radius Rb:
Eine Kugel ist dadurch charakterisiert, dass die Krümmung in jedem Punkt der Oberfläche in alle Richtungen gleich gross ist. Anders das Rotationsellipsoid. Da hängt die Krümmung in einem Punkt P davon ab, in welche Richtung wir sie untersuchen. Eine Ausnahme bilden nur die beiden Pole, wo die Krümmung wie bei einer Kugel in alle Richtungen gleich bleibt. Sonst kann man wie bei jeder gekrümmten Fläche nach den beiden Hauptkrümmungsrichtungen in einem beliebigen Punkt P auf der Oberfläche fragen. Jeder Punkt mit Ausnahme der Pole weist zwei solche Richtungen auf: die eine Richtung ist gegeben durch den Meridian, der durch die beiden Pole und P läuft, und die andere ist senkrecht zum Meridian durch den Punkt P. Die beiden zueinander im rechten Winkel stehenden Krümmungskreise haben die Radien N = RQ (Querkrümmung) und M = RM (Meridiankrümmung):
Man erkennt folgende Gesetzmässigkeiten:
- Für φ = 0° (also am Äquator) erreichen die beiden Krümmungsradien ihren kleinsten Wert mit RQ = a und RM = a ∙ (1 – ε²); am Pol haben die beiden Krümmungsradien ihren grössten Wert, nämlich , in Übereinstimmung mit der Aussage, dass am Pol die Krümmung in alle Richtungen gleich gross ist.
- RQ ist nie kleiner als RM, meist sogar grösser. Nur an den Polen sind die beiden Werte gleich.
- Für φ ≈ 35° wird RM = b, für φ ≈ 55° wird RM = a.
Für einen Punkt in der Höhe H über dem Rotationsellipsoid der Erde kann man dreidimensionale, geozentrische kartesische Koordinaten [XG, YG, ZG] berechnen, wenn die geografischen Koordinaten λ und φ sowie die Höhe H über dem Rotationsellipsoid bekannt sind:
worin RQ der oben bestimmte Radius der Querkrümmung ist.
Abstand zweier Punkte auf der Erdoberfläche[Bearbeiten]
Für Näherungsrechnungen oder Rechnungen, die keine hohen Genauigkeitsansprüche stellen, kann man die Erde als Kugel behandeln und den Abstand zweier Punkte mit den Verfahren der Sphärischen Trigonometrie bestimmen: hat der erste Ort A die Koordinaten (λA, φA) und der zweite Ort B die Koordinaten (λB, φB), und liegen beide Orte auf der Kugeloberfläche, so liefert der sphärische Cosinussatz für den Winkel ψ zwischen den beiden Orten
Mit dem Erdradius R⊕ = 6371 km erhalten wir daraus für die Distanz s zwischen A und B:
Wenn ψ sehr klein wird, dann stellt der sphärische Cosinussatz hohe Ansprüche an die Genauigkeit der Funktion arccos.
Auf dem Ellipsoid mit grosser Halbachse a und Abplattung f gibt es keine geschlossene Formel, um die Länge einer Kurve von A nach B zu berechnen. Es gibt jedoch Näherungslösungen, die immerhin ein besseres Ergebnis als die Kugelnäherung liefern. Eines davon ist das Verfahren von Andoyer, das ein Resultat mit einer Genauigkeit in der Grössenordnung von f2 ergibt:
Wiederum seien der Ort A mit den Koordinaten (λA, φA) und der Ort B mit den Koordinaten (λB, φB) gegeben. Dann berechne man die Hilfsgrössen F, G, L, S, C, ω, R, D, H1 und H2:
Mit diesen Hilfsgrössen berechnet sich der gesuchte Abstand s zu:
Der Abstand zweier Meridiane ist gleich der Länge des von ihnen ausgeschnittenen Breitenkreisbogens. Dieser Abstand ist abhängig von der geografischen Breite. Für den Abstand zweier Meridiane, die genau 1° auseinander liegen, finden wir am Äquator den Wert 111.32 km; in 45° Breite (z.B. Mitteleuropa) 78.85 km und in 66⅔° Breite (mittleres Norwegen, nördliches Schweden) noch 44.22 km. Der Abstand zweier Breitenkreise wird längs eines von ihnen geschnittenen Meridians gemessen und ist nach dem eingangs Gesagten nicht mehr direkt berechenbar. Liegen die beiden Breitenkreise aber nur sehr wenig auseinander – z.B. 1° –, dann können wir ihren Abstand als Bogenlänge auf dem Krümmungskreis berechnen. Im Gegensatz zur Kugel wird dieser Abstand damit auf dem Ellipsoid ebenfalls breitenabhängig: er ist in geringen Breiten (Tropen) etwas kleiner als in hohen Breiten. Am Äquator finden wir dafür den Wert 110.57 km, in 45° Breite 111.13 km und in 66⅔° Breite 111.52 km. Der Abstand zwischen dem 89. Breitenkreis und dem Pol ist dann 111.69 km.

Steigerung der Genauigkeit[Bearbeiten]
Für sehr genaue Rechnungen müssen weitere Effekte berücksichtigt werden: Die Richtung der Normalen auf die Horizontebene zum Zenit muss nicht mit der Richtung übereinstimmen, die ein Lot anzeigt. Eine solche Lotabweichung ist ein Hinweis darauf, dass an dieser Stelle der wahre Erdkörper – das sog. Geoid – von einem Rotationsellipsoid abweicht. In den Alpen ist dieser Effekt am grössten und kann im Maximum bis zu 1' = 60" erreichen, im Mittel etwa die Hälfte davon. Ebenfalls beachtet werden muss, dass der Nordpol nicht ein fester Punkt ist, sondern im Laufe der Zeit eine Torkelbewegung um eine mittlere Lage ausführt, die sog. Polbewegung. Die Werte werden regelmässig in den Bulletins des IERS publiziert. Damit nicht zu verwechseln ist die Tatsache, dass geografischer und magnetischer Pol nicht miteinander übereinstimmen und eine Kompassnadel daher nicht genau nach geografisch Nord weist. Dieser als Missweisung oder (magnetische) Deklination bezeichnete Richtungsunterschied ist auf genauen Karten angegeben.
Höhe über Meer[Bearbeiten]
Die Höhe korrekt zu definieren ist eine schwierige Aufgabe. Im Idealfall würde Normalnull der Oberfläche des Rotationsellipsoids entsprechen. Wenn die Erde zudem einen vollkommen homogenen Aufbau hätte, so wäre dies die (mittlere) Oberfläche der Meere, und Höhenangaben wären eindeutig. Da dies nicht der Fall ist, passen sich die Oberflächen der Gewässer dem lokalen Schwerefeld an. Da kann es schon mal vorkommen, dass das Wasser von einem Ort mit etwas geringerem Abstand von der Oberfläche des Rotationsellipsoids zu einem Punkt mit etwas grösserem Abstand fliesst – vorausgesetzt, am „höheren“ Ort ist das Schwerefeld stärker und „suggeriert“ dem Wasser so eine tiefere Lage. Wichtig ist, dass bei Höhenangaben immer genau angegeben werden muss, was man als Nulllage wählt. Das GPS-System gibt die Höhe über dem Rotationsellipsoid an. Die Höhenangaben in den einzelnen Ländern (z.B. für Karten und Vermessungen) beziehen sich auf den Pegelstand an einem ausgewählten Ort: die Schweiz bindet ihren Referenzpunkt – den Repère Pierre du Niton im Hafenbecken von Genf – an den Pegel von Marseille, Deutschland an den Pegel von Amsterdam und Österreich an jenen von Triest. Zudem legen die Länder nicht immer den gleichen Referenzkörper zugrunde, von dem aus sie die Höhe messen. Dies kann zu merklichen Abweichungen in der Höhenangabe der verschiedenen Länder führen. Auffällig werden solche Unterschiede vor allem in Grenznähe, wo sich Karten mit ihren Angaben der verschiedenen Höhen zweier Länder überlappen können.
Die wichtigste Konsequenz ist aber die, dass zwischen den Höhenangaben auf der Basis der Nivellierung mit Bezug auf den Repère Pierre de Niton und den Höhenangaben, die sich auf das WGS84-Ellipsoid beziehen, eine Differenz von 45 bis 50 m entsteht. Um so viel sind WGS84-Koordinaten in der Schweiz höher als LV-Koordinaten. Genauer: die Differenz beträgt 46 m im Nordosten der Schweiz (Bodenseeregion; östlich von Samnaun) und 53 m im Südwesten (Genf). Dazwischen nimmt sie regelmässig zu.
Wie heikel diese Geschichte mit den Höhenangaben ist, erfuhren schweizerische und deutsche Ingenieure 2002/2003: zwischen dem deutschen Städtchen Laufenburg, am Nordufer des Rhein gelegen, und dem schweizerischen Städtchen gleichen Namens am Südufer des Flusses sollte eine neue Brücke über den Fluss gebaut werden. Zwar war den beteiligten Ingenieuren klar, dass die Referenzsysteme von Deutschland und der Schweiz bezüglich Höhenmessung nicht übereinstimmen – immerhin macht die Differenz rund 27 cm aus. Nur wurde der Unterschied in die falsche „Richtung“ korrigiert: statt den Unterschied auszugleichen, wurde er verdoppelt. Im letzten Moment wurde entdeckt, dass die Brücke 54 cm zu tief über den Rhein wächst, und so wurde auf deutscher Seite die Zufahrt rund einen halben Meter tiefer gelegt, um den Rechenfehler wieder auszugleichen[3].
Übungen
- Das 1.8 m Teleskop im Lowell Observatory in Flagstaff (AZ) hat die Koordinaten λ = –111° 32' 09.3", φ = +35° 05' 48.6", H = 2206 m. Berechnen Sie für diesen Beobachtungsort ρ ∙ sin ϕ' und ρ ∙ cos ϕ', ρ, φ und φ' sowie die räumlichen kartesischen Koordinaten X, Y und Z.
- Zeigen Sie: auf der geografischen Breite von ungefähr 35° (genauer: 35.310°) erreicht der Radius der Meridiankrümmung den Wert , auf der geografischen Breite von ungefähr 55° (genauer: 54.781°) den Wert RM = a.
- Das Gemini North Teleskop auf Mauna Kea (Hawaii) hat die Koordinaten λ = –155° 28' 08.6", φ = +19° 49' 25.7", H = 4213 m, das Gemini South Teleskop in Cerro Pachon (Chile) hat die Koordinaten λ = –70° 44' 12.1", φ = –30° 14' 26.7", H = 2722 m (beide Datensätze im WGS 84). Berechnen Sie den Abstand der beiden Teleskope nach der einfachen Methode auf einer Kugeloberfläche bzw. nach dem Verfahren von Andoyer.
Nachweise:
- ↑ Die Zahlenwerte entstammen der Publikation »Department of Defense World Geodetic System 1984«, National Imagery and Mapping Agency, Technical Report NIMA TR8350.2, 3 January 2000
- ↑ WGS 84: World Geodetic System 1984; GPS: Global Positioning System
- ↑ Zeitungsartikel im Weser Kurier in Bremen, Zeitungsartikel in der Süddeutschen Zeitung.
Karten[Bearbeiten]
Karten gibt es heute von fast allen Regionen in ganz verschiedenen Massstäben. Zwischen 1 : 1 000 000 (oder noch kleiner) und 1 : 100 000 sind es Übersichtskarten, Länderkarten oder geografische Karten, die eine grossflächige Orientierung in einem Gebiet ermöglichen. Zwischen 1 : 100 000 und 1 : 50 000 sind es Umgebungskarten, und Karten mit einem Massstab grösser als 1 : 50 000 – insbesondere die bei Berggängern in der Schweiz so beliebten Karten von swisstopo im Massstab 1 : 25 000, die ein recht genaues Bild des Geländes vermitteln – sind Detailkarten, früher oft auch als Messtischblätter bezeichnet. Massstäbliche Darstellungen grösser als etwa 1 : 10 000 oder 1 : 5 000 werden Pläne genannt (z.B. Katasterpläne). Der Massstab gibt an, um wieviel mal eine Strecke, die in der Karte gemessen wird, in der Wirklichkeit grösser ist.
Beispiel:
Hat ein Fluss auf einer Karte im Massstab 1 : 250 000 eine Breite von 3 mm, dann ist er in Wirklichkeit 750 000 mm = 750 m breit.
Trotz des Detailreichtums sollte man auch nicht aus einer 25 000-er Karte geografische Koordinaten für astronomische Zwecke herauslesen. Dies aus drei Gründen:
- Damit die Karte noch lesbar bleibt, können Signaturen nicht kleiner als 1 mm gross gedruckt werden, unabhängig von ihrer wahren Grösse. Das entspricht in Wirklichkeit einer Ausdehnung von 25 m. Selbst wenn man sehr genau misst, kann man zudem mit den üblichen Instrumenten nicht genauer als 0.2 mm messen, was einem Fehler von mindestens 5 m in der Realität entspricht.
- Der zweite Grund hat damit zu tun, dass sich das Papier, auf dem die Karte gedruckt wird, verändert: einerseits schrumpft das ganze Blatt (oder dehnt sich aus), was direkt den Gesamtmassstab verändert. Andererseits bricht das Papier durch häufigen Gebrauch entlang den Faltlinien, so dass die Abstände über die Faltlinien hinweg wiederum unkontrolliert verändert werden.
- Der dritte Grund besteht darin, dass die für astronomische Zwecke benötigten geografischen Koordinaten nur sehr ungenau abgelesen werden können. Projiziert und mit dem Gitternetz dargestellt werden nämlich ganz andere Koordinaten: LV95+ Koordinaten im Falle der Schweiz, Gauss-Krüger-Koordinaten im Falle Deutschlands und Österreichs. Die Umrechnung dieser Kartenkoordinaten in geografische Koordinaten ist zwar möglich, aber keinesfalls trivial.
Für ein mobiles Teleskop zum „Spazierensehen“ am Nachthimmel mag die Genauigkeit, wie sie eine Detailkarte bietet, noch angehen, für ein ortsfestes Teleskop mit der Ambition der Deep-Sky-Fotografie muss es schon genauer sein. Dafür besorgt man sich einen Plan des Quartiers im Massstab 1 : 5 000, 1 : 2 500 oder 1 : 1 000 beim Vermessungsamt oder bei der zuständigen GIS-Fachstelle. Oft findet man solche Karten auch im Internet, wobei die Angebote aber kostenpflichtig sind[1]
Es soll kurz auf die Koordinaten der Landeskarten eingegangen werden. In allen drei Ländern wird der Erdkörper durch das Bessel-Ellipsoid von 1841 angenähert, das für Europa eine besonders gute Anpassung liefert. Es unterscheidet sich aber vom WGS84-Ellipsoid, das die gesamte Erde annähert:
| Parameter | Bessel-Ellipsoid 1841 | WGS84-Ellipsoid |
| grosse Halbachse a | 6 377 397.155 m | 6 378 137.0 m |
| kleine Halbachse b | 6 356 078.963 m | 6 356 752.314 m |
| Abplattung f | 1 / 299.152 812 85 | 1 / 298.257 223 563 |
Ebenfalls allen drei Koordinatensystemen gemeinsam ist, dass es sich um Abstände von einem festen Punkt handelt. Doch damit sind die Gemeinsamkeiten erschöpft. Insbesondere wählen die drei Länder unterschiedliche Fundamentalpunkte. Damit bezeichnet man jenen Punkt, in dem die Höhe des Ellipsoids mit dem Erdkörper übereinstimmt, der also letztlich für die Höhenangabe relevant ist. Im Falle der Schweiz ist es der Fundamentalpunkt der Geostation Zimmerwald[2]. Dazu steht in der Verordnung von swisstopo über Geoinformation vom 26.05.2008 im Art. 3:
c. Der Fundamentalpunkt liegt in der Geostation Zimmerwald (BE). Die ellipsoidischen
Koordinaten des Fundamentalpunktes sind derart festgelegt, dass das Zentrum der
Kartenprojektion im ideellen Meridianzentrum der alten Sternwarte Bern die
ellipsoidische Länge λ = 7°26'22.50" und die ellipsoidische Breite ϕ = 46°57'08.66"
erhält. Die ellipsoidische Höhe des Fundamentalpunktes beträgt h = 897.361 m.
Die Position eines Ortes wird vom Ellipsoid auf eine Kugel und von da auf einen schiefachsigen Zylinder projiziert und dann in die Ebene abgewickelt. Im alten System LV03 hatte die alte Sternwarte als Fundamentalpunkt die Koordinaten y = 600 000.00 m (Rechtswert) und x = 200 000.00 m (Hochwert). Dadurch lag der Nullpunkt dieses Systems in der Nähe von Bordeaux. Im neuen System LV95 bleibt die alte Sternwarte das Projektionszentrum und erhält neu die Koordinaten y = 2 600 000.000 m (Rechtswert) und x = 1 200 000.000 m (Hochwert). Der Nullpunkt wird also 2 000 000 m weiter westlich und 1 000 000 m weiter südlich verlegt. Bis ins Jahr 2016 soll die Umstellung von LV03 auf LV95 erfolgt sein.
Swisstopo bietet auf ihrer Homepage einen Online-Rechner an, mit dessen Hilfe man einzelne LV03- und WGS84-Daten ineinander umwandeln kann (NAVREF). Daneben wird ein Onlineprogramm namens REFRAME angeboten, mit dessen Hilfe man ganze Datendateien in die unterschiedlichsten Referenzsysteme transformieren kann.
Beim System der Gauss-Krüger-Koordinaten, die in Deutschland gebräuchlich sind, wird wie folgt vorgegangen: die Erde wird in N-S-orientierte Streifen von 3° Längenunterschied aufgeteilt, wobei jeder Streifen durch den in seiner Mitte verlaufenden Meridian charakterisiert wird: λ1 = 3° ± 1½° entspricht dem Streifen mit der Nummer 1, λ2 = 6° ± 1½° entspricht Streifen 2, λ3 = 9° ± 1½° entspricht Streifen 3, usw. Allgemein entspricht dem Streifen, dessen Mittelmeridian die Länge λk = k ∙ 3° hat (k ∈ ℕ) die Streifennummer k = λM/3°. Üblicherweise überlappen sich die Streifen etwas, so wird z.B. in Deutschland nicht λM ± 1½°, sondern λM ± 1⅔° gewählt. Dadurch überlappen sich zwei benachbarte Streifen auf einer Breite von 20'. Um die Erde wird ein Zylinder umbeschrieben, dessen Durchmesser dem Erddurchmesser entspricht. Auf diesen Zylinder werden die Meridianstreifen projiziert und dann abgewickelt. Als rechtwinklige, kartesische Koordinaten gibt man einerseits die Entfernung eines Punktes vom Mittelmeridian in Meter, wobei man zur Vermeidung negativer Werte noch 500 000 m dazu addiert und zur eindeutigen Identifizierung die Streifennummer voran stellt. Dieser horizontal gemessene Wert heisst der Rechtswert. Die zweite Achse weist entlang des Mittelmeridians nach Norden und hat ihren Ursprung auf dem Äquator: der Hochwert gibt den Abstand eines Punktes vom Äquator in Meter, gemessen auf dem Mittelmeridian.
Beispiel:
Rechtswert 3 494 314, Hochwert 5 554 129 (ein Punkt in Hanau) bedeutet: im dritten Gauss-Krüger-Streifen, dessen Mittelmeridian 9°E entspricht, 5686 m westlich des Mittelmeridians, und 5554 km nördlich des Äquators. Die Umrechnung auf geografische Koordinaten liefert λ = +8° 55' 14" und φ = +50° 07' 28".
Auch für die Gauss-Krüger-Koordinaten werden im Internet Programme und Online-Dienste für die Umrechnung angeboten: das Programm GEOTRANS der National Geospatial-Intelligence Agency, das Online-Umrechnungsprogramm der Uni Karlsruhe und das Programm HAMQTH. Eine Übersicht über Online-und Download-Transformationsrechner findet sich ebenfalls.
In Österreich wird ein modifiziertes Gauss-Krüger-System benützt. Um nicht vier Meridianstreifen benutzen zu müssen, wählt man als Mittelmeridian nicht ganzzahlige Vielfache von 3°, sondern die drei Meridiane 10° 20' (M28), 13° 20' (M31) und 16° 20' (M34)[3]. Der Nullpunkt für den Rechtswert liegt nicht einheitlich für alle Streifen 500 km westlich des Mittelmeridians, sondern für M28 150 km, für M31 450 km und für M34 750 km westlich des Mittelmeridians. Der Nullpunkt für den Hochwert liegt nicht auf dem Äquator, sondern 5000 km nördlich davon.
Alle hier vorgestellten Kartenprojektionen haben ein gemeinsames Problem: das Gitter ist rechtwinklig kartesisch. Der Mittelmeridian wird als vertikale Gerade in Nord-Süd-Richtung abgebildet, fällt also mit der zentralen Gitterlinie zusammen. Alle anderen Meridiane im Streifen sind aber keine parallelen Geraden mehr, denn der Abstand zwischen zwei Meridianen ist umso kleiner, je weiter nördlich gemessen wird. Die anderen Meridiane konvergieren also zum Mittelmeridian, wenn wir im Streifen nach Norden wandern. Wir bezeichnen den Richtungsunterschied zwischen „Gitternord“, also der Nordrichtung, wie sie durch das Koordinatengitter suggeriert wird und für den Mittelmeridian auch richtig ist, und der wirklichen oder geografischen Nordrichtung als Meridiankonvergenz χ (ein Winkel). Ein Näherungswert dafür kann wie folgt berechnet werden:
worin Δλ der Längenunterschied, φ die geografische Breite, y' der Abstand vom Mittelmeridian und der Erdradius bedeuten.
Übungen
- Bestimmen Sie die Koordinaten (Rechtswert, Hochwert) im (alten) Koordinatensystem LV03 der Schweiz folgender vier Punkte: Höchi Flue oberhalb Egerkingen (im Solothurner Jura); die Gipfel des „Dreigestirns“ im Berner Oberland, Eiger, Mönch und Jungfrau. Benutzen Sie dazu die von map-plus online zur Verfügung gestellte skalierbare Schweizerkarte. Wandeln Sie die LV03-Koordinaten anschliessend mittels NAVREF in WGS84-Koordinaten um.
- Berechnen Sie die Entfernung Höchi Flue – Jungfrau und Eiger – Mönch mit den voranstehenden Daten auf drei verschiedene Arten: a) mit den LV03-Koordinaten als Problem der ebenen Geometrie; b) mit der Näherung der Kugelform für die Erde und den WGS84-Koordinaten; c) mit der Näherungslösung von Andoyer für das WGS84-Ellipsoid (vgl. Sie auch das voranstehende Kapitel). Welche Feststellungen können Sie treffen?
Nachweise:
- ↑ Hier als typisches Beispiel ZUGIS, die GIS-Fachstelle des Kantons Zug (Schweiz): http://www.zugis.ch/
- ↑ Im Vorgängersystem LV03 war es die alte Sternwarte in der Länggasse in der Stadt Bern.
- ↑ Auf diese Längen kommt man wie folgt: der westlichste Punkt Europas, die Kanareninsel El Hierro, hat die Länge –17° 40' (bezogen auf Greenwich). Da sich Österreich ca. von +9°30' bis +17° 10' (bezogen auf Greenwich) erstreckt, entspricht dies 27° 10' bzw. 34° 50' östlich von El Hierro bzw. in den auf El Hierro bezogenen Meridianstreifen von 28°, 31° und 34°.












![{\displaystyle {\begin{aligned}\tau \;=\;{\frac {\Delta }{c}}\;&=\;{\frac {149\;597\;871\;{\text{km/AE}}\cdot \Delta }{299\;792.458\;{\text{km/s}}}}\;\\&=\;499.004\;784\;837\cdot \Delta \;[{\text{s}}]\;\\&=\;0.005\;775\;5183\cdot \Delta \;[{\text{d}}]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d976dd11692737c5014bbd1c9276a31ac5e69f90)



































