Lineare Unabhängigkeit von Vektoren – Serlo „Mathe für Nicht-Freaks“
Motivation
[Bearbeiten]Grundmotivation
[Bearbeiten]Aus der Schule kennen wir Vektoren als Pfeile in der Ebene oder im Raum. Sowohl die Ebene als auch der Raum sind Vektorräume. Aber worin unterscheiden sie sich?
Eine spontane Antwort könnte lauten: „Die Ebene ist zweidimensional und der Raum dreidimensional.“ Das bringt uns aber gleich zu weiteren Fragen:
- Was ist die Dimension eines Vektorraums?
- Wie können wir sie definieren?
In der Definition des Vektorraums kommt der Begriff „Dimension“ nämlich nicht vor...
Intuition der Dimension
[Bearbeiten]
Der Begriff „Dimension“ beschreibt, in wie viele unabhängige Richtungen geometrische Objekte in einem Raum ausgedehnt sein können. Die Objekte können sich auch in genau so vielen unabhängigen Richtungen im Raum bewegen („Freiheitsgrade der Bewegung“).
Die Ebene hat zwei Dimensionen – die Breite und die Länge. Sie ist flach, kein Objekt der Ebene kann in die Höhe reichen. Eine Kugel kann als dreidimensionales Objekt also nicht Teil der Ebene sein. Im Gegensatz dazu besitzt der Raum mit Länge, Breite und Höhe drei Dimensionen. Eine Kugel kann so Teil eines Raums sein.
Wir fassen zusammen: Die Dimension entspricht intuitiv der Anzahl der unabhängigen Richtungen, in die sich ein geometrisches Objekt ausdehnen bzw. bewegen kann. Für die Definition der Dimension müssen wir also folgende Fragen beantworten:
- Was ist eine Richtung in einem Vektorraum?
- Wann sind zwei Richtungen unabhängig?
- Wie kann die Anzahl der unabhängigen Richtungen bestimmt werden?
Herleitung der Definition
[Bearbeiten]
Was ist eine Richtung in einem Vektorraum?
[Bearbeiten]Nehmen wir als Beispiel den Vektorraum der Ebene. Eine Richtung können wir mit einem Pfeil darstellen:

Nun ist ein Pfeil nichts anderes als ein Vektor. Mit Hilfe von Vektoren können also Richtungen repräsentiert werden. Dabei dürfen wir nicht den Nullvektor verwenden. Als Pfeil der Länge Null hat dieser nämlich keine Richtung. Dies können wir auf beliebige Vektorräume verallgemeinern:
Jeder Vektor ungleich dem Nullvektor repräsentiert eine Richtung in einem Vektorraum.
Die Richtung, in die der Vektor zeigt ist , also der Spann des Vektors . Zu diesem Spann gehören alle Streckungen des Richtungsvektor und beschreibt damit die Gerade, die durch aufgespannt wird:
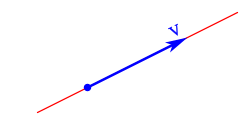
Von der Geraden zur Ebene
[Bearbeiten]Um jetzt von der Geraden zur Ebene zu kommen, benötigen wir nicht nur einen Vektor sondern mehrere, genauer gesagt mindestens zwei Vektoren (). Dies erschließt sich ja auch intuitiv, da man eine Ebene nur mit zwei Vektoren eindeutig aufspannen kann. Deshalb brauchen wir einen weiteren, linear unabhängigen Vektor. Was bedeutet in diesem Fall „unabhängig“? Zunächst stellen wir fest, dass der neue Vektor nicht der Nullvektor sein darf. Dieser gibt nämlich keine Richtung an. Weiterhin darf der neue Vektor auch kein Vielfaches des ursprünglichen Vektors sein, also . Dies gilt auch für Spiegelungen des Geradenvektors, also Vielfache mit einem negativen Faktor.
-
Der Vektor ist eine Streckung des Vektors um einen positiven Faktor. Dieser Vektor ist keine von unabhängige Richtung.
-
Der Vektor ist eine Spiegelung von mit einem negativem Faktor. Die Richtung von ist nicht unabhängig von .
-
Die Richtung von ist unabhängig von . Beide Vektoren zusammen spannen eine Ebene auf.
Wir fassen zusammen: Der neue Vektor ist genau dann unabhängig vom Richtungsvektor , wenn dieser nicht auf der Geraden liegt. Es muss also für alle reellen Zahlen sein. Der neue Vektor darf also nicht im Spann des anderen liegen. Die beiden Vektoren haben nur den Nullpunkt als Schnittpunkt.
Von der Ebene zum Raum
[Bearbeiten]Wir haben gesehen, dass wir eine Ebene durch zwei unabhängige Vektoren charakterisieren können. Nun möchten wir von der Ebene zum Raum übergehen. Auch hier müssen wir eine unabhängige Richtung hinzunehmen. Was ist aber eine zur Ebene unabhängige Richtung?
Der neue Vektor darf nicht der Nullvektor sein, weil dieser keine Richtung angibt. Der neue Vektor darf auch nicht in der Ebene liegen, da so keine neue Richtung beschrieben wird. Genau dann wenn der neue Vektor nicht in der Ebene liegt, dann zeigt er in eine neue unabhängige Richtung:
-
Der Vektor liegt in der Ebene, welcher von den Vektoren und aufgespannt wird. Damit zeigt in keine von und unabhängige Richtung.
-
Der Vektor liegt nicht in der von und aufgespannten Ebene. Alle drei Vektoren spannen den kompletten Raum auf und damit zeigt in eine von und unabhängige Richtung.
Wie können wir diese Erkenntnis mathematisch formulieren? Seien und die beiden Richtungsvektoren, die die Ebene aufspannen. Diese Ebene ist dann gleich der Menge . Die Ebene ist damit die Menge aller Summen für reelle Zahlen . Damit der neue Vektor nicht in der Ebene liegt, muss für alle sein. Damit ist unabhängig von und genau dann, wenn ist. Mit anderen Worten: .
Verständnisfrage: Wir hatten zuerst gefordert, dass der neue Vektor nicht der Nullvektor sein darf. Warum reicht es aus, dass für alle ist? Warum impliziert dies, dass ist?
Für ist . Da auch für der neue Vektor ungleich sein soll, folgt .
Verständnisfrage: Reicht es aus, dass kein Vielfaches von beziehungsweise ist?
Nein, nehme zum Beispiel . Wenn unabhängig von ist, dann ist weder eine Streckung von noch von . Jedoch liegt dieser Vektor in der von und aufgespannten Ebene und bildet damit keine unabhängige Richtung von und .
Ein erstes Kriterium für lineare Unabhängigkeit
[Bearbeiten]Fassen wir zusammen: Zur Beschreibung einer Geraden benötigten wir einen Vektor ungleich dem Nullvektor. Im Übergang von der Geraden zur Ebene mussten wir einen zu unabhängigen Vektor hinzufügen. Unabhängigkeit von zur Richtung bedeutet hier, dass nicht in der von beschriebenen Geraden liegt. Es musste also für alle sein.
Im zweiten Schritt haben wir der Ebene eine neue Richtung hinzugefügt, die von den beiden Vektoren und unabhängig ist. Hier manifestiert sich Unabhängigkeit darin, dass nicht in der von und aufgespannten Ebene liegt. Es muss also für alle reellen Zahlen und sein. Dies können wir für eine beliebige Anzahl an Vektoren verallgemeinern (jedoch kann man sich das nicht mehr so gut vorstellen):
Der Vektor ist unabhängig von den Vektoren , wenn für alle ist.
In der obigen Beschreibung kommt die Summe vor. Eine solche Summe wird Linearkombination der Vektoren bis genannt. Wir können auch sagen, dass linear unabhängig ist, wenn . Die Beschreibung kann geändert werden zu:
Der Vektor ist unabhängig von den Vektoren , wenn nicht als Linearkombination der Vektoren bis dargestellt werden kann.
Hier haben wir geklärt, wann ein Vektor unabhängig von anderen Vektoren ist. Reicht dies aus, um die Unabhängigkeit von Vektoren zu beschreiben?! Nimm folgende drei Vektoren , und :

Weil kein Vektor ein Vielfaches eines anderen Vektoren ist, zeigen die drei Vektoren paarweise gesehen in unabhängige Richtungen. Beispielsweise ist unabhängig zu und ist unabhängig zu . Insgesamt gesehen sind die drei Vektoren jedoch nicht unabhängig voneinander, weil sie alle in einer Ebene liegen. Es ist und damit ist abhängig zu und . Dementsprechend müssen wir für die lineare Unabhängigkeit zwischen , und fordern:
- ist unabhängig zu und : Es ist für alle .
- ist unabhängig zu und : Es ist für alle .
- ist unabhängig zu und : Es ist für alle .
An dieser Stelle sei betont, dass es nötig ist alle drei Bedingungen zu fordern. Würden wir auf die letzten beiden Bedingungen verzichten, so würde die erste Forderung zwar garantieren, dass der Vektor linear unabhängig von den Vektoren und ist, aus dieser Forderung ist aber nicht klar, dass und linear unabhängig voneinander sind. Dies muss nicht erfüllt sein, wodurch dann die drei Vektoren untereinander wieder nicht linear unabhängig wären.
Es darf also keiner der drei Vektoren als Linearkombination der anderen zwei Vektoren dargestellt werden können. Ansonsten ist nämlich mindestens einer der Vektoren zu den anderen Vektoren abhängig. Dies können wir für eine beliebige Anzahl von Vektoren verallgemeinern:
Definition (Erstes Kriterium für lineare Unabhängigkeit)
Vektoren bis sind linear unabhängig, wenn keiner der Vektoren als Linearkombination der anderen Vektoren dargestellt werden kann. Damit muss gelten:
- Es ist für alle .
- Es ist für alle .
- ...
- Es ist für alle .
Es sind also bis linear unabhängig, wenn für alle und ist.
Vom ersten Kriterium zur formalen Definition
[Bearbeiten]Mit unserem ersten Kriterium, welches wir oben gefunden haben, haben wir bereits eine passende Definition für die lineare Unabhängigkeit von Vektoren gefunden. Wir wollen im Folgenden versuchen eine knappere äquivalente Definition zu finden, mit Hilfe derer wir die lineare Unabhängigkeit von Vektoren leichter untersuchen können.
Vektoren sind genau dann unabhängig voneinander, wenn sich kein Vektor als Linearkombination der anderen Vektoren darstellen lässt. Daraus werden wir ein weiteres Kriterium für lineare Unabhängigkeit herleiten, welches weniger rechenaufwändig ist. Nehmen wir Vektoren , bis aus einem Vektorraum , die nicht unabhängig sind. Es gibt also einen Vektor, der durch die anderen dargestellt werden kann. Sei dieser Vektor. Es gibt damit Streckungsfaktoren (Skalare) bis , so dass gilt:
Diese Gleichung können wir umstellen, indem wir auf beiden Seiten rechnen ( ist der Nullvektor des Vektorraums ):
Dies ist eine sogenannte nichttriviale Linearkombination des Nullvektors. Eine nichttriviale Linearkombination des Nullvektors ist eine Linearkombination mit dem Ergebnis , bei dem mindestens ein Koeffizient ungleich ist. Für ist nämlich immer . Dies ist die sogenannte triviale Linearkombination des Nullvektors, bei der alle Koeffizienten gleich sind. Diese triviale Linearkombination kannst du stets bilden, egal welche Vektoren bis du wählst. Wenn bis abhängig voneinander sind, gibt es neben der trivialen Linearkombintion noch mindestens eine nichttriviale Linearkombination des Nullvektors (wie wir es oben gesehen haben). Also:
Wenn bis abhängig voneinander sind, dann kann der Nullvektor durch bis durch mindestens eine nichttriviale Linearkombination dargestellt werden.
Anders ausgedrückt:
sind abhängig Es existiert eine nicht triviale Linearkombination von durch
Nun können wir das Prinzip der Kontraposition anwenden. Dieses besagt, dass eine Aussage genau dann gilt, wenn . Also gilt auch:
Es existiert keine nichttriviale Linearkombination von durch sind unabhängig
Damit haben wir ein Kriterium für Unabhängigkeit gefunden. Wenn der Nullvektor nur trivial durch eine Linearkombination von bis dargestellt werden kann, dann sind diese Vektoren unabhängig. Dieses Kriterium kann aber auch als Definition der linearen Unabhängigkeit benutzt werden. Hierzu müssen wir die Rückrichtung der obigen Implikation zeigen. Wenn es eine nichttriviale Linearkombination des Nullvektors gibt, dann sind die betrachteten Vektoren abhängig voneinander.
Seien also bis Vektoren, für die es eine nichttriviale Linearkombination des Nullvektors gibt. Es gibt also Koeffizienten (Skalare) bis , derart dass und mindestens einer der Koeffizienten bis ungleich ist. Sei dieser Koeffizient. Dann ist
Wegen können wir beide Seiten mit multiplizieren. Wir erhalten damit
Auf beiden Seiten können wir nun addieren:
Damit kann als Linearkombination der anderen Vektoren dargestellt werden und somit sind die Vektoren bis abhängig voneinander. Dies beweist insgesamt die formale Definition der linearen Unabhängigkeit:
Definition (Zweites Kriterium für Lineare Unabhängigkeit)
Die Vektoren sind linear unabhängig, wenn mit ihnen der Nullvektor nur durch die triviale Linearkombination dargestellt werden kann, d.h. wenn wir haben mit , dann folgt für alle .
Wenn es mindestens eine nichttriviale Linearkombination des Nullvektors gibt, sind die betrachteten Vektoren linear abhängig voneinander.
Definition des Begriffs Familie
[Bearbeiten]Wir haben oben davon gesprochen, dass eine Ansammlung von Vektoren linear unabhängig ist. Aber was ist diese Ansammlung von Vektoren aus mathematischer Sicht? Wir kennen bereits den Begriff einer Menge. Also ist es naheliegend auch als Menge aufzufassen. Passt diese Auffassung intuitiv zur linearen Unabhängigkeit? Nehmen wir als Beispiel zwei gleiche Vektoren mit . Beide zeigen in die selbe Richtung und spannen keine zwei unabhängigen Richtungen auf. Damit sind sie intuitiv linear abhängig. Und tatsächlich kann man einen als Linearkombination des anderen schreiben und zwar als . Damit sind die Vektoren auch streng mathematisch linear abhängig. Eine Menge darf allerdings nur verschiedene Elemente enthalten. Das heißt, die Menge, die und enthält ist . Die Menge enthält also nur ein Element und erfasst keine Doppelungen von Vektoren.
Wir brauchen also einen neuen mathematischen Begriff, der auch Doppelungen erfasst. Dies ist der Begriff der Familie:
Definition (Familie)
Eine Familie von Elementen einer Menge besteht aus einer Indexmenge , so dass zu jedem Index ein Element gehört.
Ist eine endliche Menge, sprechen wir von einer endlichen Familie.
Ist , so nennt man Teilfamilie von , umgekehrt heißt Oberfamilie zu .
Formal kann man eine Familie als eine Abbildung der Indexmenge in die Menge ansehen. Im Gegensatz zu Mengen dürfen in Familien Elemente mehrfach vorkommen, nämlich wenn sie zu verschiedenen Indizes gehören.
Ist die Menge abzählbar, so lassen sich die Elemente der Familie nummerieren: . Die Indexmenge darf aber auch überabzählbar ein, z.B. . In diesem Fall kann nicht als Folge geschrieben werden. Der Begriff "Familie" enthält also alle "Folgen", und umfasst sogar noch größere Ansammlungen von mathematischen Objekten.
Wenn wir also sagen die Vektoren und sind linear abhängig können wir es dadurch ausdrücken, dass die Familie mit linear abhängig ist.
Oft schreibt man (nicht ganz exakt) , wenn die Elemente von sind und aus dem Zusammenhang klar ist, wie die Indexmenge aussieht. Analog bedeutet , dass es ein gibt mit .
Hiermit können wir die zweite Definition der linearen Unabhängigkeit neu aufschreiben:
Definition (Zweites Kriterium für Lineare Unabhängigkeit, Neufassung)
Die Familie von Vektoren ist linear unabhängig, wenn mit ihnen der Nullvektor nur durch die triviale Linearkombination dargestellt werden kann, d.h. wenn wir haben mit , dann folgt für alle .
Allgemeine Definition der linearen Unabhängigkeit
[Bearbeiten]Motivation
[Bearbeiten]Wir haben oben zwei Definitionen dafür kennen gelernt, dass endlich viele Vektoren linear unabhängig sind:
- Eine etwas sperrige: Die Vektoren sind unabhängig, wenn sich kein Vektor als Linearkombination der anderen schreiben lässt. Also darf nicht vorkommen.
- Eine etwas kompaktere: Der Nullvektor lässt sich nur als triviale Linearkombination darstellen. Also aus folgt .
Bisher haben wir nur endlich viele Vektoren betrachtet. Was passiert bei unendlich vielen Vektoren? Kann es überhaupt unendlich viele linear unabhängige Vektoren geben? Wir bräuchten einen Vektorraum, der unendlich viele linear unabhängige Richtungen hat. Wir wissen intuitiv, dass der Vektorraum höchstens zwei und der höchstens drei unabhängige Richtungen hat. Wir brauchen also einen viel "größeren" Vektorraum, um unendlich viele unabhängige Richtungen zu bekommen. Wir betrachten also einen Vektorraum , in dem jeder Vektor unendlich viele Koordinaten besitzt: mit . Demnach entspricht einer reellen Folge und ist der Folgen-Vektorraum, oder kurz Folgenraum.
Im haben wir die linear unabhängigen Einheitsvektoren . Wir können diese Konstruktion fortsetzen und erhalten für die Vektoren mit der an der -ten Stelle und sonst .
Die unendlich vielen Vektoren bilden eine Familie . Diese Familie repräsentiert intuitiv "unendlich viele verschiedene Richtungen" in und ist damit intuitiv gesehen linear unabhängig. Es ergibt also Sinn, lineare Unabhängigkeit für unendlich viele Vektoren so zu definieren, dass eine linear unabhängige Familie ist. Die "etwas sperrige Definition 1." in der Aufzählung wäre dafür prinzipiell geeignet: Wir könnten sie einfach kopieren und sagen "eine Familie von Vektoren ist linear unabhängig, wenn sich kein als Linearkombination der anderen schreiben lässt". Tatsächlich kann in keiner der als Linearkombination der anderen Vektoren geschrieben werden. Daher ergibt die Definition an dieser Stelle schon einmal Sinn. Allerdings gibt es unendlich viele und damit unendlich viele Bedingungen!
Wir betrachten lieber die "etwas kompaktere Definition 2.": "Vektoren sind linear unabhängig, wenn nur durch die triviale Linearkombination dargestellt werden kann." Was bedeutet diese Formulierung in diesem Beispiel explizit? Wir haben also eine Linearkombination der gegeben. Linearkombinationen sind endlich, das heißt wir haben endlich viele Vektoren und , sodass
Wir müssen nun zeigen, dass alle sind, da dann die obige Linearkombination die triviale Linearkombination der ist. Dies geht genauso wie im , nur dass wir hier unendlich viele Einträge miteinander vergleichen müssen.
Was müssen wir nun tun, um eine allgemeine Definition für allgemeine Familien und allgemeine Vektorräume zu bekommen? Die "etwas kompaktere Definition 2." überträgt sich fast wortwörtlich: "Eine Familie von Vektoren ist linear unabhängig, wenn nur durch die triviale Linearkombination dargestellt werden kann." Für die ausgeschriebene Implikation, können wir für die Endlichkeit der Linearkombination von unserer Sprache von Familien gebrauch machen: Wir ersetzen die Doppelindizes durch das Wort "Teilfamilie".
Definition
[Bearbeiten]Definition (Lineare Abhängigkeit und Unabhängigkeit von Vektoren)
Seien ein Körper, ein -Vektorraum und eine Familie von Vektoren aus .
heißt linear unabhängig, wenn für jede endliche Teilfamilie und alle mit folgendes gilt:
Eine Familie heißt linear abhängig, wenn sie nicht linear unabhängig ist.
Warnung
Linearkombinationen aus Elemeten einer Menge bestehen immer aus endlich vielen Summanden, auch wenn die Menge unendlich ist.
Z.B. ist die Familie linear unabhängig im Vektorraum , obwohl . Denn die Exponentialfunktion ist keine endliche Linearkombination der Monome.
Hinweis
Häufig spricht man von "linear unabhängigen Mengen" statt von "linear unabhängigen Familien". Wir haben uns oben schon überlegt, dass es sinnvoll ist hier Familien zu verwenden, da Familien anders als Mengen auch Doppelungen von Elementen erfassen. Man kann aus jeder Menge die Familie konstruieren. Damit überträgt sich der Begriff linear (un-)abhängig auch auf Mengen. Linear unabhängige Familien enthalten keinen Vektor doppelt. Familien ohne doppelte Elemente korrespondieren über obige Konstruktion zu Mengen. Will man nun eine Familie von linear unabhängigen Vektoren haben (z.B. in den Voraussetzungen eines Satzes), kann man auch gleich nach einer Menge linear unabhängiger Vektoren fragen. Wenn wir nun testen wollen, ob eine Familie von Vektoren linear unabhängig ist, können wir diese nicht erst in eine Menge umwandeln. Denn dort verschwinden Dopplungen und diese sorgen für lineare Abhängigkeit.
Hinweis
Die Definition der linearen (Un-)Abhängigkeit bezieht sich auf Teilfamilien eines Vektorraums. Diese dürfen Vektoren merfach enthalten und sogar überabzählbar sein.
Bei endlichen Familie sprechen wir alternativ über die Elemente, d.h. die Aussage "Die Familie ist linear (un-)abhängig" wird zu " sind linear (un-)abhängig".
Folgerungen aus der Definition
[Bearbeiten]Umformulierung der Definition für endliche Teilfamilien
[Bearbeiten]Wir haben eine Definition von linearer Unabhängigkeit von beliebeigen Teilfamilien eines Vektorraums . Stimmt diese mit unserer alten Definition für endliche Teilfamilien überein? Intuitiv sollten sie für endliche Teilfamilien übereinstimmen, da wir die allgemeine Definition aus unserer alten Definition hergeleitet haben. Der folgende Satz zeigt das nochmal formal:
Satz (Lineare Unabhängigkeit bei endlich vielen Vektoren)
- Die Vektoren sind genau dann linear unabhängig, wenn aus mit folgt, dass ist.
- Die Vektoren sind genau dann linear abhängig, wenn es Elemente des Körpers bis gibt, die nicht alle sind, aber ist.
Beweis (Lineare Unabhängigkeit bei endlich vielen Vektoren)
Wir beweisen zuerst die erste Aussage. Wir müssen eine Äquivalenz zeigen.
Sei zunächst linear unabhängig. Mit der Defintion der linearen Unabhängigkeit folgt, dass für jede endliche Teilfamilie von und für alle Skalare mit folgendes gilt:
ist eine endliche Teilfamilie von sich selbst. Deshalb folgt für alle aus , dass für alle .
Gelte nun umgekehrt, dass für alle aus folgt, dass ist. Wir wollen zeigen, dass linear unabhängig ist. Sei dafür eine endliche Teilfamilie von . Das heißt . Seien mit Skalare mit
Wir erweitern diese Summe, so dass sie über alle läuft. Dafür definieren wir für alle . Dann
Aus unserer Voraussetzung folgt, dass und damit auch für alle . Also ist linear unabhängig.
Die zweite Aussage ist genau die logische Kontraposition der ersten. Denn wir haben gezeigt mit den zwei Aussagen
" ist linear unabhängig"
""
Der zweite Punkt ist die Aussage . Das ist aber äquivalent zu und damit äquivalent zu der ersten Aussage.
Zurückführen der Definition auf endliche Teilfamilien
[Bearbeiten]Wir haben lineare Unabhängigkeit für eine beliebige Familie von Vektoren definiert, also auch für unendlich viele Vektoren. Aber in der Definition müssen wir nur eine Aussage für endliche Teilfamilien zeigen: Für alle mit gilt folgendes:
Im vorherigen Satz haben wir gesehen, dass diese Aussage genau lineare Unabhängigkeit von ist.
Satz (Kriterium mit endlichen Teilfamilien)
- Eine Familie ist genau dann linear unabhängig, wenn jede endliche Teilfamilie linear unabhängig ist.
- Eine Familie ist genau dann linear abhängig, wenn sie eine endliche linear abhängige Teilfamilie enthält.
Beweis (Kriterium mit endlichen Teilfamilien)
Zuerst beweisen wir die erste Aussage. Wir müssen eine Äquivalenz zeigen. Sei eine linear unabhängige Familie von Vektoren aus . Wir zeigen, dass jede endliche Teilfamilie von linear unabhängig ist.
Sei dafür eine endliche Teilfamilie von . Aus unserer Definition für lineare Unabhängigkeit folgt, dass für alle Skalare mit folgendes gilt:
Mit dem vorherigen Satz folgt, dass linear unabhängig ist.
Gelte nun umgekehrt, dass jede endliche Teilfamilie von linear unabhängig ist. Wir zeigen, dass . Sei dafür eine endliche Teilfamilie von . Wir wollen zeigen, dass für alle Skalare mit folgendes gilt:
Nach unserer Voraussetzung ist linear unabhängig. Also folgt wieder mit dem vorherigen Satz, dass für alle Skalare mit die Aussage
gilt.
Die zweite Aussage ist genau die logische Kontraposition der ersten. Denn wir haben gezeigt mit den zwei Aussagen
" ist linear unabhängig"
"jede endliche Teilfamilie von ist linear unabhängig"
Der zweite Punkt ist die Aussage . Das ist aber äquivalent zu und damit äquivalent zu der ersten Aussage.
Übersicht
[Bearbeiten]Folgende Eigenschaften können mit wenigen Beweisschritten aus der Definition der linearen Unabhängigkeit hergeleitet werden. Dabei sei im Folgenden ein Körper und ein -Vektorraum:
- Jede Teilfamilie einer Familie linear unabhängiger Vektoren ist linear unabhängig. Umgekehrt ist jede Oberfamilie einer Familie linear abhängiger Vektoren wieder linear abhängig.
- Sei ein einzelner Vektor. Dann ist genau dann linear unabhängig, wenn ist. Also "fast immer". Umgekehrt ist jede Familie (egal wie groß) linear abhängig, sobald sie den Nullvektor enthält.
- Seien . Die Vektoren und sind genau dann linear abhängig, wenn es ein mit der Eigenschaft oder gibt.
- Ist eine Familie von Vektoren linear abhängig, so kann einer von ihnen als Linearkombination der anderen dargestellt werden.
Teilfamilien linear unabhängiger Vektoren sind linear unabhängig
[Bearbeiten]Eine linear unabhängige Familie bleibt linear unabhängig, wenn man Vektoren wegnimmt. Lineare Abhängigkeit bleibt hingegen erhalten, wenn man weitere Vektoren hinzufügt. Intuitiv zerstört also das Hinzufügen von Vektoren tendenziell die lineare Unabhängigkeit und kann durch weiteres Hinzufügen auch nicht wiederhergestellt werden.
Satz
- Jede Teilfamilie einer Familie linear unabhängiger Vektoren ist linear unabhängig.
- Jede Oberfamilie einer Familie linear abhängiger Vektoren ist linear abhängig.
Beweis
Wir zeigen zuerst die erste Aussage. Sei eine Familie von linear unabhängigen Vektoren aus und eine beliebige Teilfamilie von . Seien und mit
Wegen liegen die Vektoren auch in . Da linear unabhängig ist, gilt . Also ist linear unabhängig.
Daraus folgern wir die zweite Aussage. Sei eine Familie von linear abhängigen Vektoren aus und eine beliebige Oberfamilie von . Angenommen ist linear unabhängig. Dann folgt mit der vorherigen Aussage, dass auch als Teilfamilie von linear unabhängig ist. Das ist aber ein Widerspruch, weil linear abhängig ist.
Familie mit Nullvektor ist linear abhängig
[Bearbeiten]Wann ist eine Familie mit genau einem Vektor linear unabhängig? Diese Frage lässt sich leicht beantworten: immer dann, wenn dieser Vektor nicht der Nullvektor ist. Umgekehrt ist jede Familie mit dem Nullvektor linear abhängig. Inklusive die, die nur den Nullvektor selbst enthält.
Satz (Familie mit Nullvektor ist linear abhängig)
- Der Nullvektor ist linear abhängig.
- Wenn linear abhängig ist, so ist .
- Eine Familie von Vektoren, die den Nullvektor enthält, ist linear abhängig.
Beweis (Familie mit Nullvektor ist linear abhängig)
- Es ist . Es gibt also eine nicht triviale Linearkombination des Vektors , die als Ergebnis hat. Damit ist der Nullvektor linear abhängig.
- Ist linear abhängig, so gibt es mit . Da , gibt es ein multiplikatives Inverses . Multiplizieren wir die Gleichung mit so erhalten wir . Also muss der Nullvektor sein.
- Diese Behauptung folgt einfach aus 1. und dem Satz über die lineare Abhängigkeit von Oberfamilien linear abhängiger Familien.
Bei zwei Vektoren sind genau die Streckungen linear abhängig
[Bearbeiten]Wann ist eine Familie mit zwei Vektoren linear unabhängig? Wir können die Frage beantworten, indem wir sagen, wann das Gegenteil der Fall ist. Also wann sind zwei Vektoren linear abhängig? Lineare Abhängigkeit zweier Vektoren gilt genau dann, wenn beide "auf einer Geraden liegen", d.h. der eine Vektor eine Streckung des anderen ist.
Satz
Seien . Die Vektoren und sind genau dann linear abhängig, wenn es ein mit der Eigenschaft oder gibt.
Beweis
Wir müssen folgende zwei Implikationen beweisen:
- und sind linear abhängig
- und sind linear abhängig
Beweisschritt: Erste Implikation
Ist einer der beiden Vektoren der Nullvektor, dann sind nach dem vorherigen Satz und linear abhängig. Seien also und . Es sei so gewählt, dass ist. Dies ist o.B.d.A. möglich, denn falls das nicht geht, vertauschen wir die Bezeichnungen der beiden Vektoren. Wir verwenden also anstelle von und anstelle von . Laut Voraussetzung muss ein existieren, sodass die Gleichung mit den neuen Bezeichnungen gilt.
Nun gilt . Damit haben wir den Nullvektor als nichttriviale Linearkombination dargestellt. Das bedeutet, dass und linear abhängig sind.
Beweisschritt: Zweite Implikation
Seien dafür und linear abhängig. Dann gibt es nach Definition eine nichttriviale Linearkombination des Nullvektors. Es existieren also so, dass und nicht beide Null sind und die Gleichung gilt. Wir betrachten den Fall, dass ist. Dann folgt aus der Gleichung und damit
Falls jedoch ist, dann muss sein. Analog zur Rechnung von eben kannst du nachrechnen, dass dann ist mit .
Von linear abhängigen Vektoren kann einer als Linearkombination der anderen dargestellt werden
[Bearbeiten]Bei endliche vielen Vektoren hatten wir mit der Definition begonnen, dass Vektoren linear abhängig sind, wenn einer der Vektoren als Linearkombination der anderen geschrieben werden kann (erste Definition). Wir haben schon gesehen, dass diese Definition äquivalent dazu ist, dass der Nullvektor als Linearkombination der Vektoren geschrieben werden kann (zweite Definition). Bei der allgemeinen Definition mit möglicherweise unendlich vielen Vektoren haben wir die Version mit dem Nullvektor (die zweite) als unsere Definition genutzt. Und man kann tatsächlich zeigen, dass auch im allgemeinen Fall die erste Definition dazu äquivalent ist:
Satz
Sei ein -Vektorraum und seien linear abhängige Vektoren, aber seien linear unabhängig. Dann gibt es derart, dass ist.
Wie kommt man auf den Beweis?
Wegen der linearen Abhängigkeit von gibt es , die nicht alle gleich sind, so dass . Wir wollen als Linearkombination der schreiben. Also wollen wir die Gleichung nach auflösen. Wir können umformen zu
Nun wollen wir durch teilen. Das geht nur, wenn . Also zeigen wir, dass der Fall nicht auftreten kann. Angenommen . Dann folgt
Wir wissen, dass linear unabhängig sind. Also sind alle gleich . Dadurch sind alle gleich . Das ist ein Widerspruch. Deshalb kann nicht passieren.
Beweis
Da linear abhängig sind, gibt es mit , wobei nicht alle gleich sind. Daher gilt
Wir zeigen zuerst . Nehmen wir also an, es wäre . Dann wäre
Wegen der linearen Unabhängigkeit der folgt daraus auch für alle . Das kann aber nicht sein, da nicht alle Null sind. Also gilt . Wir können damit durch dividieren und die gesuchte Linearkombination ist
Setze nun , dann ist und genau das war zu zeigen.
Lineare Unabhängigkeit und eindeutige Linearkombinationen
[Bearbeiten]Wir betrachten in diesem Abschnitt den Zusammenhang zwischen Linearer Unabhängigkeit und Linearkombinationen genauer. Dafür machen wir uns klar, was es bedeutet, wenn die Vektoren linear abhängig oder unabhängig sind. Angenommen die Vektoren sind linear abhängig. Aus unserer Definition der linearen Unabhängigkeit wissen wir, dass es dann eine nicht triviale Nulldarstellung geben muss, da mindestens ein Skalar für ein ist. Wir machen uns dies anhand des folgenden Beispiels klar
Beispiel (Lineare Abhängigkeit und nicht triviale Nulldarstellung)
Betrachten wir die Vektoren . Diese sind linear abhängig, da
Durch Umformung dieser Gleichung erhalten wir eine Darstellung des Nullvektors:
Neben dieser Darstellung gibt es auch die sogenannte triviale Darstellung des Nullvektors, bei der jeder Vorfaktor gleich Null ist:
Wegen der linearen Abhängigkeit kann der Nullvektor über zwei Wege über eine Linearkombination dargestellt werden.
Unabhängig davon, ob die betrachtete Familie von Vektoren linear unabhängig ist oder nicht, gibt es stets die triviale Nulldarstellung, in dem alle Skalare den Wert haben:
Bei linearer Abhängigkeit der Vektoren ist die Darstellung der Null nicht mehr eindeutig. Wir können unsere Ergebnisse bisher in einem Satz zusammenfassen und verallgemeinern:
Satz (Lineare Unabhängigkeit und eindeutige Linearkombinationen)
Sei ein Vektorraum und .
Alle Linearkombinationen von Vektoren aus sind eindeutig linear unabhängig.
Beweis (Lineare Unabhängigkeit und eindeutige Linearkombinationen)
Wir zeigen die Kontraposition:
Es gibt eine Linearkombination von Vektoren aus , die nicht eindeutig ist ist linear abhängig.
Beweisschritt: ""
Wir nehmen an, dass es gibt, so dass es verschiedene Darstellungen von durch Vektoren aus gibt:
Sei mit und mit und . Subtraktion der beiden Gleichungen liefert
Da die Darstellungen von unterschiedlich sind, gibt es mindestens einen Faktor für . Damit sind die Vektoren nach Definition linear abhängig und damit ist auch linear abhängig.
Beweisschritt: " "
Wenn linear abhängig ist, enthält eine linear abhängige Teilmenge .
Dann gibt es außer der trivialen Darstellung der Null mindestens eine weitere: wegen der linearen Abhängigkeit gibt es Faktoren , die nicht alle Null sind, mit
Also haben wir gezeigt, dass es dann zwei Darstellungen von als Linearkombination dieser Vektoren gibt. Damit sind Linearkombinationen nicht eindeutig.
Übungsaufgaben
[Bearbeiten]Aufgabe 1
[Bearbeiten]Aufgabe (Lineare Unabhängigkeit)
Zeige, dass die Vektoren linear unabhängig sind.
Lösung (Lineare Unabhängigkeit)
Wir müssen zeigen, dass durch die gegebenen Vektoren der Nullvektor nur trivial dargestellt werden kann. Dies bedeutet, dass die folgende Gleichung mit den reellen Zahlen nur die Lösung besitzt:
Hieraus ergibt sich:
Nun sind zwei Spaltenvektoren genau dann gleich, wenn jede Komponente gleich ist. Also müssen folgende Gleichungen gelten:
Es ist also . Wenn wir dies in einsetzen, erhalten wir . Damit haben wir gezeigt, dass aus der Gleichung folgt, dass alle Koeffizienten , und gleich sind. Somit sind die drei Vektoren linear unabhängig.
Aufgabe 2
[Bearbeiten]Aufgabe (Lineare Abhängigkeit)
Zeige dass die folgende Menge von vier Vektoren linear abhängig ist:
Lösung (Lineare Abhängigkeit)
Nach Definition sind die Vektoren und genau dann linear abhängig, wenn wir eine nichttriviale Linearkombination der Null mit ihnen finden. Eine solche ist beispielsweise durch
gegeben. Also sind die Vektoren linear abhängig.
Lösung (Lineare Abhängigkeit, Alternative)
Vektoren sind linear abhängig, wenn einer sich als Linearkombination der anderen drei darstellen lässt. Nun kann der Vektor als Linearkombination der anderen dargestellt werden:
Damit sind die Vektoren linear abhängig.
Aufgabe 3
[Bearbeiten]Aufgabe (Trigonometrische Polynome)
Sei mit für alle . Das heißt, dass eine -periodische Funktion ist. Wir betrachten die Menge der -periodischen Funktionen. Diese bilden einen -Vektorraum.
Sind die Funktionen linear unabhängig?
Wie kommt man auf den Beweis? (Trigonometrische Polynome)
Wir untersuchen, wie man die Nullfunktion als Linearkombination der drei Funktionen schreiben kann. Dazu bestimmen wir die Werte von in der Gleichung . Das können wir tun, indem wir drei verschiedene Werte für einsetzen und dann das entstehende Gleichungssystem lösen.
Dafür eignen sich Werte, für die wir die Werte des Kosinus explizit kennen – zum Beispiel und . Denn es gilt und .
Lösung (Trigonometrische Polynome)
Seien , sodass
für alle gilt. Wir wollen zeigen, dass gelten muss. Indem wir für die Werte und einsetzen, erhalten wir folgendes Gleichungssystem für die :
Das Gleichungssystem kann nun auf verschiedene Arten gelöst werden. Wir stellen zunächst die erste Gleichung um und erhalten . Das können wir in die zweite Gleichung einsetzen und erhalten , also . Wenn wir unsere Ergebnisse jetzt in die dritte Gleichung einsetzen, haben wir . Dies ist äquivalent dazu, dass gilt. Daraus folgt direkt .
Damit haben wir die Koeffizienten und eindeutig bestimmt. Das heißt, es gibt keine nichttriviale Linearkombination der . Die Funktionen sind also linear unabhängig.
Aufgabe 4
[Bearbeiten]Aufgabe (Lineare (Un-)abhängigkeit?)
Beweise oder widerlege die folgende Aussage:
Seien . Die Menge ist genau dann linear abhängig, wenn jeder der Vektoren eine Linearkombination der anderen beiden ist.
Wie kommt man auf den Beweis? (Lineare (Un-)abhängigkeit?)
Damit die Menge linear abhängig ist, reicht es, wenn zwei der drei Vektoren ein Vielfaches des jeweils anderen sind, während der Dritte linear unabhängig von den beiden sein kann. Mit dieser Überlegung können wir uns ein Gegenbeispiel zu der Aussage konstruieren.
Lösung (Lineare (Un-)abhängigkeit?)
Die Aussage ist nicht richtig. Wir betrachten die Menge
Dann können wir den Nullvektor als nichttriviale Linearkombination der drei Vektoren darstellen:
Damit ist die Menge linear abhängig. Allerdings ist der Vektor keine Linearkombination der anderen beiden.
Aufgabe 5
[Bearbeiten]Aufgabe (Linear unabhängige Vektoren im )
Beweise: Im Vektorraum der -Tupel über dem Körper sind die Vektoren , bis linear unabhängig.
Lösung (Linear unabhängige Vektoren im )
Wir müssen zeigen, dass wir den Nullvektor eindeutig als Linearkombination der Vektoren darstellen können. Betrachten wir also die Linearkombination der Vektoren mit für . Es soll gelten
Dies können wir als lineares Gleichungssystem auffassen als
Damit haben wir gezeigt, dass die eindeutig bestimmt sind und den Wert besitzen. Nach Definition der linearen Unabhängigkeit haben wir damit gezeigt, dass die Vektoren linear unabhängig sind.
Aufgabe 6
[Bearbeiten]Aufgabe (Linear unabhängige Vektoren bei Endomorphismus)
Sei ein Körper und ein Endomorphismus des -Vektorraums . Sei , sodass für eine feste natürliche Zahl gilt: für und . Hierbei bedeutet das -malige Anwenden der Abbildung auf den Vektor . Beweise, dass dann die Vektoren linear unabhängig sind.
Wie kommt man auf den Beweis? (Linear unabhängige Vektoren bei Endomorphismus)
Wir müssen zeigen, dass für mit
schon gilt. Wir können dafür versuchen, die einzelnen aus dieser Gleichung zu erhalten: Wir wissen, dass gilt. Wenden wir nun auf diese Gleichung an, so erhalten wir
Wir haben damit erreicht, dass wir einen Summanden verloren haben. Damit haben wir unser Problem auf einen Fall mit Summanden reduziert. Das heißt, indem wir mit einer Induktion vorgehen, können wir die Aussage jetzt folgern.
Lösung (Linear unabhängige Vektoren bei Endomorphismus)
Wir führen eine Induktion nach durch, um obige Idee, die Anzahl der Vektoren um einen Vektor zu reduzieren anwenden zu können.
Aussageform, deren Allgemeingültigkeit für bewiesen werden soll:
Ist mit für alle und , so ist linear unabhängig.
1. Induktionsanfang:
Wir müssen zeigen, dass und linear unabhängig sind, wenn und gelten. Das heißt wir müssen zeigen, dass für mit schon erfüllt sein muss. Nun ist
Weil gilt, muss gelten. Dann ist nach Wahl von und auch . Mit dem gleichen Argument folgt nun .
2. Induktionsschritt:
2a. Induktionsvoraussetzung:
Ist mit für alle und , so ist linear unabhängig.
2b. Induktionsbehauptung:
Ist mit für alle und , so ist linear unabhängig.
2c. Beweis des Induktionsschritts:
Seien , sodass gilt. Dann ist
Indem wir die Induktionsvoraussetzung auf anwenden, erhalten wir, dass gilt. Damit ist . Weil ist, muss gelten. Also ist linear unabhängig.


























































































































































![{\displaystyle {\begin{aligned}0_{V}&=\sum _{j\in J}\lambda _{j}\cdot v_{j}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ 0_{V}{\text{ addieren}}\right.}\\[0.3em]&=\sum _{j\in J}\lambda _{j}\cdot v_{j}+0_{V}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ 0_{V}=\sum _{i\in J\setminus \{1,\ldots ,n\}}0\cdot v_{i}\right.}\\[0.3em]&=\sum _{j\in J}\lambda _{j}\cdot v_{j}+\sum _{i\in J\setminus \{1,\ldots ,n\}}0\cdot v_{i}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ 0=\lambda _{i}\right.}\\[0.3em]&=\sum _{j\in J}\lambda _{j}\cdot v_{j}+\sum _{i\in J\setminus \{1,\ldots ,n\}}\lambda _{i}\cdot v_{i}\\[0.3em]&=\sum _{k\in \{1,\ldots ,n\}}\lambda _{k}\cdot v_{k}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5861ebdddfb3c1694af2118229efbbfe9b99847)





































![{\displaystyle {\begin{aligned}\beta \cdot w&=-\alpha \cdot v&&\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{beide Seiten der Gleichung multiplizieren mit }}\beta ^{-1}}\\[0.3em]w&=\,\beta ^{-1}\cdot (-\alpha \cdot v)&&\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{Assoziativgesetz der skalaren Multiplikation berücksichtigen}}}\\[0.3em]&=\,-(\beta ^{-1}\alpha )\cdot v&&\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{setze }}{\lambda \colon =-(\beta ^{-1}\alpha )}}\\[0.3em]&=\,\lambda \cdot v\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b5396250aa1bcd1fa9da27c7d51ddf799a4b10e)


















































![{\displaystyle {\begin{aligned}&\rho _{1}\cdot {\begin{pmatrix}1\\1\\0\end{pmatrix}}+\rho _{2}\cdot {\begin{pmatrix}0\\1\\0\end{pmatrix}}+\rho _{3}\cdot {\begin{pmatrix}0\\1\\1\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{skalare Multiplikation ausführen}}\right.}\\[0.3em]\implies &{\begin{pmatrix}\rho _{1}\\\rho _{1}\\0\end{pmatrix}}+{\begin{pmatrix}0\\\rho _{2}\\0\end{pmatrix}}+{\begin{pmatrix}0\\\rho _{3}\\\rho _{3}\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Vektoraddition ausführen}}\right.}\\[0.3em]\implies &{\begin{pmatrix}\rho _{1}\\\rho _{1}+\rho _{2}+\rho _{3}\\\rho _{3}\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddd97afb5c4865a576e6527fd53f1c1ef4780add)































![{\displaystyle {\begin{aligned}x={\frac {\pi }{2}}&:&\lambda _{1}-\lambda _{3}&=0\\[0.3em]x=\pi &:&\lambda _{1}-\lambda _{2}+\lambda _{3}&=0\\[0.3em]x=0&:&\lambda _{1}+\lambda _{2}+\lambda _{3}&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1400d8d1e5652d95c5e39023edf85b6996ae5c3d)
































![{\displaystyle {\begin{aligned}0=F(0)&=F(\lambda _{0}v+\lambda _{1}F(v)+\dots +\lambda _{n}F^{n}(v))\\[0.3em]&=\lambda _{0}F(v)+\lambda _{1}F^{2}(v)+\dots +\lambda _{n}F^{n+1}(v)\\[0.3em]&=\lambda _{0}F(v)+\lambda _{1}F^{2}(v)+\dots +\lambda _{n-1}F^{n}(v).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1de9590d8f7252c3de95aa4ce5260e12d74a3a3c)









![{\displaystyle {\begin{aligned}0=F(0)&=F(\lambda \cdot v+\mu \cdot F(v))\\[0.3em]&=\lambda \cdot F(v)+\mu \cdot F^{2}(v)\\[0.3em]&=\lambda \cdot F(v)\\[0.3em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac174efa65a06223304484fe6dfa30f23df5d9b6)








![{\displaystyle {\begin{aligned}0=F(0)&=F(\lambda _{0}\cdot v+\lambda _{1}\cdot F(v)+\dots +\lambda _{n+1}\cdot F^{n+1}(v))\\[0.3em]&=\lambda _{0}\cdot F(v)+\lambda _{1}\cdot F^{2}(v)+\dots +\lambda _{n+1}\cdot F^{n+2}(v)\\[0.3em]&=\lambda _{0}\cdot F(v)+\dots +\lambda _{n}\cdot F^{n+1}(v)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3251b14e68e28324427e37a60597e2dc2fe1290c)



