Folgenkriterium der Stetigkeit: Folgenstetigkeit – Serlo „Mathe für Nicht-Freaks“

Motivation und Herleitung

Erste Beispiele

Betrachte den Grenzwert $\lim _{n\to \infty }\exp \left({\tfrac {1}{n}}\right)$. In der Schule würde man diesen Grenzwert folgendermaßen ausrechnen:

${\begin{aligned}\lim _{n\to \infty }\exp \left({\frac {1}{n}}\right)&=\exp \left(\lim _{n\to \infty }{\frac {1}{n}}\right)\\[0.5em]&{\color {OliveGreen}\left\downarrow \ \lim _{n\to \infty }{\frac {1}{n}}=0\right.}\\[0.5em]&=\exp(0)\\&=1\end{aligned}}$

Diese Rechnung ergibt intuitiv Sinn: Wenn ${\tfrac {1}{n}}\to 0$, dann sollte $\exp \left({\tfrac {1}{n}}\right)\to \exp(0)$ sein. Doch können wir so argumentieren? Ist es erlaubt, den Limes in die Funktion reinzuziehen? Betrachte hierzu die Vorzeichenfunktion $\operatorname {sgn}(x)$, welche das Vorzeichen von $x$ zurückgibt:

$\operatorname {sgn}(x)={\begin{cases}1&x>0\\0&x=0\\-1&x<0\end{cases}}$

Wegen ${\begin{aligned}{\tfrac {1}{n}}>0\end{aligned}}$ gilt:

$\lim _{n\to \infty }\operatorname {sgn} \left({\tfrac {1}{n}}\right)=\lim _{n\to \infty }1=1\neq 0=\operatorname {sgn}(0)=\operatorname {sgn} \left(\lim _{n\to \infty }{\frac {1}{n}}\right)$

Also ist $\lim _{n\to \infty }\operatorname {sgn} \left({\tfrac {1}{n}}\right)\neq \operatorname {sgn} \left(\lim _{n\to \infty }{\tfrac {1}{n}}\right)$. Dies zeigt, dass man den Limes nicht ohne Weiteres in eine Funktion hineinziehen kann. Im Funktionsplot sieht man, warum dies bei $\exp(x)$, jedoch nicht bei $\operatorname {sgn}(x)$ möglich ist. Bei $\exp(x)$ konvergiert nämlich die Folge $\left(\exp \left({\tfrac {1}{n}}\right)\right)_{n\in \mathbb {N} }$ gegen $\exp(0)$, wenn $n\to \infty$ geht:

exp(1/n) konvergiert gegen exp(0) für n gegen unendlich

Bei der Vorzeichenfunktion gibt es einen Sprung im Graphen bei $x=0$, und deswegen konvergiert die Folge $\left(\operatorname {sgn} \left({\tfrac {1}{n}}\right)\right)_{n\in \mathbb {N} }$ nicht gegen $\operatorname {sgn}(0)$:

sgn(1/n) konvergiert nicht gegen sgn(0) für n gegen unendlich

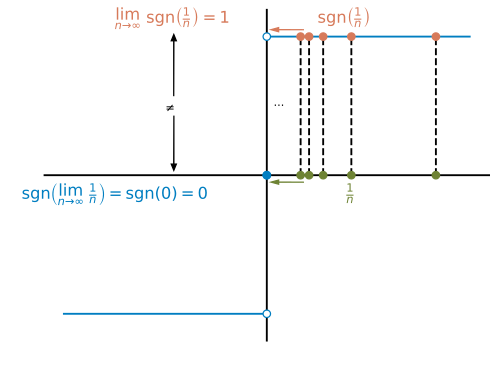
Wir stellen fest: Es gibt Funktionen, bei denen der Limes hineingezogen werden kann, und Funktionen, bei denen es nicht (immer) geht.

Sprungstellen und Stetigkeit

Wir erkennen, dass wir deswegen den Limes nicht in $\operatorname {sgn} \left({\tfrac {1}{n}}\right)$ hineinziehen können, weil der Graph der Vorzeichenfunktion an der Stelle $x=0$ „einen Sprung macht“. Wir überlegen uns nun, warum das Hineinziehen des Limes nicht möglich ist, wenn der Graph beim Grenzwert der Argumentenfolge einen Sprung macht. Nehmen wir an, dass $f$ folgenden Graphen besitzt:

Graph der Funktion f mit einem Sprung an der Stelle x0, wobei der rechtsseitige Grenzwert an der Stelle x0 existiert.

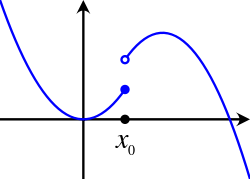
Wenn wir uns von links an $x_{0}$ annähern, dann nähern sich die Funktionswerte auch an $f(x_{0})$ an. Wenn also die Argumentenfolge fast ausschließlich (sprich: bis auf endlich viele Ausnahmen) nur aus reellen Zahlen kleiner gleich $x_{0}$ besteht, können wir den Limes hineinziehen. Dies schlägt jedoch fehl, wenn in der Argumentenfolge unendlich viele Zahlen größer als $x_{0}$ auftreten. Ihre Funktionswerte nähern sich nämlich nicht $f(x_{0})$ an, weil der Graph bei $x_{0}$ in die rechte Richtung einen Sprung macht. Durch den Sprung gibt es einen Mindestabstand, den die Funktionswerte in der Nähe und rechts von $x_{0}$ nicht unterschreiten. Der Sprung der Funktion an der Stelle $x_{0}$ verhindert, dass bei jeder Argumentenfolge der Limes hineingezogen werden kann.

Ähnliches passiert, wenn der Graph bei $x_{0}$ in die linke Richtung einen Sprung besitzt:

Graph der Funktion f mit einem Sprung an der Stelle x0, wobei der linksseitige Grenzwert an der Stelle x0 existiert.

Hier schlägt das Hineinziehen des Limes fehl, wenn die Argumentenfolge unendlich viele Zahlen kleiner als $x_{0}$ besitzt. Die Funktionswerte links von $x_{0}$ nähern sich aufgrund des Sprungs nämlich nicht $f(x_{0})$ an.

Im Übrigen ist die Situation eine andere, wenn $f$ an der Sprungstelle nicht definiert ist:

Graph der Funktion f mit einem Sprung an der Stelle x0, wo die Funktion nicht definiert ist.

Hier ergibt der Ausdruck $f\left(\lim _{n\to \infty }x_{n}\right)$ keinen Sinn, weil die Funktion an der Stelle $x_{0}$ nicht definiert ist. Deswegen müssen wir nicht betrachten, ob dort der Limes hineingezogen werden kann. An allen anderen Stellen ist der Graph von $f$ kontinuierlich und damit stetig. Wir sehen: Ein Sprung macht nur dann eine Funkion unstetig, wenn die Funktion an der Sprungstelle definiert ist.

Übergang zur formalen Definition

Nehmen wir eine Funktion $f$ mit Sprungstelle im Punkt $x_{0}$. Wenn man sich dem Argument $x_{0}$ von der einen Seite nähert, wird ein gewisser Abstand zwischen $f(x)$ und $f(x_{0})$ nie unterschritten. Dieser Mindestabstand zwischen $f(x)$ und $f(x_{0})$ wurde durch den Sprung an der Stelle $x_{0}$ verursacht. Wenn man sich von der anderen Seite an $x_{0}$ nähert, gehen die $f(x)$-Werte beliebig nah an $f(x_{0})$ heran (vorausgesetzt, dass hier keine zweite Sprungstelle vorliegt).

Für $x$-Werte, die beliebig (=„unendlich“) nahe an $x_{0}$ herankommen sollen, können wir den Folgenbegriff verwenden. Dafür beschreiben wir die $x$-Werte als Folge $(x_{n})_{n\in \mathbb {N} }$, die gegen $x_{0}$ konvergiert. Die Verwendung des Folgenbegriffs ist auch deswegen sinnvoll, weil wir für die Annäherung oft unendlich viele $x$-Werte benötigen und Folgen ebenfalls unendlich viele Glieder besitzen.

Gehen wir nun davon aus, dass wir uns von der Seite $x_{0}$ nähern, bei der unsere $f(x_{n})$ gegenüber $f(x_{0})$ einen gewissen Mindestabstand in der Nähe von $x_{0}$ nicht unterschreiten. Dieser bleibt auch im Limes $\lim _{n\to \infty }$ erhalten. Falls $\lim _{n\to \infty }f(x_{n})$ existiert, so wissen wir damit sicher, dass $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$ ist.

Nun haben wir nur die Annäherung von der Seite betrachtet, wo $f(x_{n})$ nicht gegen $f(x_{0})$ strebt. In unseren Beispielen können wir jedoch die Folge $(x_{n})_{n\in \mathbb {N} }$ so wählen, dass $\lim _{n\to \infty }f(x_{n})=f(x_{0})$ ist. Dies ist zum Beispiel der Fall, wenn unsere $x_{n}$ von der anderen Seite an $x_{0}$ streben. Damit $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$ erfüllt ist, können wir unsere gegen $x_{0}$ konvergierende Folge also nicht beliebig wählen. Jedoch existiert zumindest eine Folge $(x_{n})_{n\in \mathbb {N} }$, für die $f(x_{n})$ nicht gegen $f(x_{0})$ strebt.

Herleitung des Folgenkriteriums

Fassen wir das bisher Gefundene zusammen:

Wenn eine Funktion $f:D\to \mathbb {R}$ an der Stelle $x\in D$ einen Sprung besitzt, gibt es mindestens eine Folge $(x_{n})_{n\in \mathbb {N} }$ von Argumenten mit $\lim _{n\to \infty }x_{n}=x$ und $\lim _{n\to \infty }f(x_{n})\neq f(x)$.

Sprich: Im Fall eines Sprungs an der Stelle $x\in D$ gilt $\lim _{n\to \infty }f(x_{n})\neq f(x)=f\left(\lim _{n\to \infty }x_{n}\right)$ für mindestens eine Folge $(x_{n})_{n\in \mathbb {N} }$ von Argumenten mit Grenzwert $x$. Nun ist nach unserer Intuition eine Funktion genau dann unstetig an einer Stelle, wenn ihr Graph dort einen Sprung macht. Wir können also definieren:

Der Graph einer Funktion $f:D\to \mathbb {R}$ ist unstetig an der Stelle $x\in D$, wenn es mindestens eine Folge $(x_{n})_{n\in \mathbb {N} }$ von Argumenten mit $\lim _{n\to \infty }x_{n}=x$ und $\lim _{n\to \infty }f(x_{n})\neq f(x)$ gibt.

Um die Definition der Stetigkeit an einer Stelle zu finden, müssen wir die Negation der obigen Aussage nehmen. Nach dieser Überlegung können wir uns die Stetigkeit an einer Stelle als Abwesenheit eines Sprungs an der betrachteten Stelle vorstellen, und wir erhalten:

Eine Funktion $f:D\to \mathbb {R}$ ist an der Stelle $x\in D$ stetig, wenn für alle Folgen $(x_{n})_{n\in \mathbb {N} }$ aus $D$ mit $\lim _{n\to \infty }x_{n}=x$ gilt:

$\lim _{n\to \infty }f(x_{n})=f(x)=f\left(\lim _{n\to \infty }x_{n}\right)$

Bei Stetigkeit einer Funktion an einer Stelle kann der Limes hineingezogen werden, wenn die Argumentenfolge gegen diese Stelle konvergiert. Diese Definition der Stetigkeit ist das Folgenkriterium der Stetigkeit. Nun ist eine Funktion genau dann stetig, wenn sie an jeder Stelle ihres Definitonsbereichs stetig ist. Damit erhalten wir für die Stetigkeit einer Funktion:

Eine Funktion $f:D\to \mathbb {R}$ ist stetig, wenn für alle konvergenten Folgen $(x_{n})_{n\in \mathbb {N} }$ gilt $\lim _{n\to \infty }f(x_{n})=f(\lim _{n\to \infty }x_{n})$. Dabei müssen alle Folgenglieder $x_{n}$ und der Grenzwert $\lim _{n\to \infty }x_{n}$ Elemente des Definitionsbereiches $D$ von $f$ sein, damit die Gleichung $\lim _{n\to \infty }f(x_{n})=f\left(\lim _{n\to \infty }x_{n}\right)$ Sinn ergibt.

Wir können zusammenfassen: Bei einer stetigen Funktion kann man den Limes in die Funktion hineinziehen – unabhängig vom Grenzwert der Argumentenfolge. Weil beispielsweise die Exponentialfunktion stetig ist, kann man immer den Limes in diese Funktion hineinziehen. Die Vorzeichenfunktion ist bei $x=0$ unstetig, und damit kann der Limes nicht in die Funktion gezogen werden, wenn die Argumentenfolge gegen null konvergiert.

Definition

Erklärung des Folgenkriteriums der Stetigkeit. (YouTube-Video vom Kanal Quatematik)

Im obigen Abschnitt haben wir bereits die Definition der Stetigkeit kennengelernt. Hier haben wir festgelegt:

Definition (Folgenkriterium der Stetigkeit an einer Stelle)

Eine Funktion $f:D\to \mathbb {R}$ mit $D\subseteq \mathbb {R}$ ist stetig an der Stelle $x_{0}\in D$, wenn für alle Folgen $(x_{n})_{n\in \mathbb {N} }$ mit $\forall n\in \mathbb {N} :x_{n}\in D$ und $\lim _{n\to \infty }x_{n}=x_{0}$ gilt:

$\lim _{n\to \infty }f(x_{n})=f\left(\lim _{n\to \infty }x_{n}\right)=f(x_{0})$

Darauf aufbauend haben wir definiert, dass eine Funktion stetig ist, wenn sie an jeder Stelle stetig ist:

Definition (Folgenkriterium der Stetigkeit)

Eine Funktion $f:D\to \mathbb {R}$ mit $D\subseteq \mathbb {R}$ ist stetig, wenn für alle $x\in D$ und für alle Folgen $(x_{n})_{n\in \mathbb {N} }$ mit $\forall n\in \mathbb {N} :x_{n}\in D$ und $\lim _{n\to \infty }x_{n}=x$ gilt:

$\lim _{n\to \infty }f(x_{n})=f\left(\lim _{n\to \infty }x_{n}\right)=f(x)$

Stetigkeit garantiert uns also, dass wir den Limes in die Funktion hineinziehen können. Dies kann die Grenzwertberechnung ungemein vereinfachen, und somit ist Stetigkeit ein Konzept, auf das man bei Grenzwertberechnungen stößt.

Auswirkungen der Definition

Wir haben über unsere Vorstellung von Sprungstellen eine formale Definition von Stetigkeit gefunden. Diese hat sich im Laufe der Zeit als sinnvoll herausgestellt und wird in der mathematischen Community als Definition der Stetigkeit akzeptiert. Deswegen werden auch wir sie im Folgenden heranziehen. Somit ist die Grundlage für Entscheidungen, ob eine Funktion stetig ist, nicht mehr unsere Intuition – sondern das von uns gefundene Folgenkriterium. Dies hat gewisse Nebeneffekte. Betrachte die topologische Sinusfunktion:

$f:\mathbb {R} \to \mathbb {R} :x\mapsto {\begin{cases}\sin \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0\end{cases}}$

Ihr Graph ist:

Graph der topologischen Sinusfunktion

Bei dieser Funktion ist man sich intuitiv nicht sicher, ob sie an der Stelle $x=0$ stetig ist, denn in der Nähe davon schwingt die Funktion immer stärker. Schaut man sich den Graphen an, so sieht es (für mich) nicht nach einer gewöhnlichen Sprungstelle aus. Wenn wir aber unser Folgenkriterium der Stetigkeit heranziehen, können wir zeigen, dass die topologische Sinusfunktion an der Nullstelle trotzdem unstetig ist (Übungsaufgabe).

Als Nebenprodukt unserer Definition haben wir also neben der Sprungstelle eine andere Art der Unstetigkeit erhalten. Im Englischen wird sie essential discontinuity genannt. Diese werden bzw. müssen wir akzeptieren, sofern wir das Folgenkriterium als die Definition der Stetigkeit benutzen wollen. Es sei erwähnt, dass dies eine der Standarddefinitionen ist und wir mit einer Ablehnung wohl ziemlich einsam und verloren in der Welt der Mathematik wären.

Beispiel für das Folgenkriterium

Quadratfunktion ist stetig

Folgenkriterium: Stetigkeit der Quadratfunktion beweisen

Aufgabe (Stetigkeit der Quadratfunktion)

Zeige, dass die Quadratfunktion $f:\mathbb {R} \to \mathbb {R} :x\mapsto x^{2}$ stetig ist.

Beweis (Stetigkeit der Quadratfunktion)

Sei $f:\mathbb {R} \to \mathbb {R} :x\mapsto x^{2}$. Wir betrachten nun eine beliebige Folge $(x_{n})_{n\in \mathbb {N} }$, die gegen $x$ konvergiert. Es ist

${\begin{aligned}\lim _{n\to \infty }f(x_{n})&=\lim _{n\to \infty }x_{n}^{2}\\&=\lim _{n\to \infty }x_{n}\cdot x_{n}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ \lim _{n\to \infty }a_{n}\cdot b_{n}=\lim _{n\to \infty }a_{n}\cdot \lim _{n\to \infty }b_{n}\right.}\\[0.5em]&=\left(\lim _{n\to \infty }x_{n}\right)\cdot \left(\lim _{n\to \infty }x_{n}\right)\\&{\color {OliveGreen}\left\downarrow \ {\text{Voraussetzung}}\lim _{n\to \infty }x_{n}=x\right.}\\[0.5em]&=x\cdot x=x^{2}=f(x)\end{aligned}}$

Bei der Quadratfunktion kann der Limes also immer hineingezogen werden, womit diese Funktion stetig ist.

Anwendung des Folgenkriteriums

Anwendungsbeispiel für das Folgenkriterium

Nachdem wir bewiesen haben, dass die Quadratfunktion stetig ist, können wir immer den Limes in diese Funktion hineinziehen, ohne großartig darüber nachdenken zu müssen. Dies ist das Schöne an der Stetigkeit, wie es folgende Beispielaufgabe zeigt:

Aufgabe (Anwendung des Folgenkriteriums)

Berechne $\lim _{n\to \infty }\left(1+{\tfrac {1}{n}}\right)^{2}$.

Lösung (Anwendung des Folgenkriteriums)

Wir können die bewiesene Stetigkeit der Quadratfunktion ausnutzen, indem wir den Limes in die Quadratfunktion hineinziehen. Nach dem Folgenkriterium können wir dies machen. Damit erhalten wir:

${\begin{aligned}&\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Quadratfunktion ist stetig}}\right.}\\[0.3em]=\ &\left(\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)\right)^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ \lim _{n\to \infty }\left(a_{n}+b_{n}\right)=\lim _{n\to \infty }a_{n}+\lim _{n\to \infty }b_{n}\right.}\\[0.3em]=\ &\left(\lim _{n\to \infty }1+\lim _{n\to \infty }{\frac {1}{n}}\right)^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ \lim _{n\to \infty }{\frac {1}{n}}=0\right.}\\[0.3em]=\ &(1+0)^{2}=1\end{aligned}}$

Allgemeine Beweisskizzen

Stetigkeitsbeweise mit dem Folgenkriterium

Stetigkeit mit Hilfe des Folgenkriteriums zeigen (Beweisschema)

Um die Stetigkeit einer Funktion an einer Stelle $x_{0}$ zu beweisen, müssen wir zeigen, dass für jede Folge $(x_{n})_{n\in \mathbb {N} }$ von Argumenten mit $\lim _{n\to \infty }x_{n}=x_{0}$ gilt, dass $\lim _{n\to \infty }f(x_{n})=f(x_{0})$ ist. Dementsprechend könnte ein Beweis lauten:

Sei $f:\ldots$ eine Funktion mit $f(x)=\ldots$ und sei $x_{0}=\ldots$ gegeben. Sei $(x_{n})_{n\in \mathbb {N} }$ eine beliebige Folge von Argumenten mit $\lim _{n\to \infty }x_{n}=x_{0}$. Es gilt:

$\lim _{n\to \infty }f(x_{n})=\ldots =f(x_{0})$

Um die Stetigkeit der Funktion $f$ zu beweisen, muss das Beweisschema etwas angepasst werden:

Sei $f:\ldots$ eine Funktion mit $f(x)=\ldots$ und sei $x_{0}$ eine beliebige Zahl aus dem Definitionsbereich von $f$. Sei $(x_{n})_{n\in \mathbb {N} }$ eine beliebige Folge von Argumenten mit $\lim _{n\to \infty }x_{n}=x_{0}$. Es gilt:

$\lim _{n\to \infty }f(x_{n})=\ldots =f(x_{0})$

Unstetigkeitsbeweise mit dem Folgenkriterium

Unstetigkeit mit Hilfe des Folgenkriteriums zeigen (Beweisschema)

Um mit dem Folgenkriterium zu zeigen, dass eine Funktion $f:D\to \mathbb {R}$ an der Stelle $x_{0}\in D$ unstetig ist, muss man eine Argumentenfolge $(x_{n})_{n\in \mathbb {N} }$ mit $x_{n}\in D$ für alle $n\in \mathbb {N}$ und dem Grenzwert $x_{0}$ finden, so dass die Funktionswertfolge $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ nicht gegen $f(x_{0})$ konvergiert. Es soll also $\lim _{n\to \infty }x_{n}=x_{0}$ und $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$ gelten. Für $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$ gibt es zwei Möglichkeiten:

• Die Funktionswertfolge $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ divergiert.
• Die Funktionswertfolge $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ konvergiert, jedoch ist ihr Grenzwert ungleich $f(x_{0})$.

Ein Unstetigkeitsbeweis über das Folgenkriterium könnte zum Beispiel folgende Form aufweisen:

Sei $f:\ldots$ eine Funktion mit $f(x)=\ldots$. Diese Funktion ist unstetig an der Stelle $x_{0}=\ldots$. Wählen wir nämlich die Folge $(x_{n})_{n\in \mathbb {N} }$ mit $x_{n}=\ldots$, so liegen alle Folgenglieder im Definitionsbereich von $f$, und wir haben

$\lim _{n\to \infty }x_{n}=\ldots =x_{0}$

Jedoch ist $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$. Es ist nämlich ...Beweis, dass $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ divergiert oder dass der Grenzwert von $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ ungleich $f(x_{0})$ ist...

Zusammenhang zum Epsilon-Delta-Kriterium

Es gibt zwei Definitionen der Stetigkeit: das Epsilon-Delta-Kriterium und das Folgenkriterium. Um zu zeigen, dass beide Definitionen das gleiche Konzept beschreiben, müssen wir beweisen, dass beide Kriterien äquivalent zueinander sind. Wenn das Folgenkriterium erfüllt ist, muss auch das Epsilon-Delta-Kriterium erfüllt sein und umgekehrt.

Epsilon-Delta-Kriterium impliziert Folgenkriterium

Satz (Das Epsilon-Delta-Kriterium impliziert das Folgenkriterium)

Sei $f:D\to \mathbb {R}$ mit $D\subseteq \mathbb {R}$ eine Funktion. Wenn diese Funktion an der Stelle $x_{0}\in D$ das Epsilon-Delta-Kriterium erfüllt, dann ist auch das Folgenkriterium an der Stelle $x_{0}$ erfüllt.

Wie kommt man auf den Beweis? (Das Epsilon-Delta-Kriterium impliziert das Folgenkriterium)

Nehmen wir an, dass die Funktion $f:D\to \mathbb {R}$ an der Stelle $x_{0}\in D$ das Epsilon-Delta-Kriterium erfüllt. Es gilt also:

Zu jedem $\epsilon >0$ gibt es ein $\delta >0$, sodass $|f(x)-f(x_{0})|<\epsilon$ für alle $x\in D$ mit $|x-x_{0}|<\delta$ ist.

Wir wollen nun zeigen, dass auch das Folgenkriterium erfüllt ist. Für jede Argumentenfolge $(x_{n})_{n\in \mathbb {N} }$ mit Grenzwert $x_{0}$ soll also $\lim _{n\to \infty }f(x_{n})=f(x_{0})$ gelten. Sei also $(x_{n})_{n\in \mathbb {N} }$ eine Folge von Argumenten $x_{n}\in D$ mit $\lim _{n\to \infty }x_{n}=x_{0}$. Wir müssen nun zeigen, dass der Grenzwert der Funktionswertfolge $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ gleich $f(x_{0})$ ist. Es soll also gelten:

Zu jedem $\epsilon >0$ gibt es ein $N\in \mathbb {N}$ mit $|f(x_{n})-f(x_{0})|<\epsilon$ für alle $n\geq N$.

Sei $\epsilon >0$ beliebig. Wir müssen nun ein $N\in \mathbb {N}$ finden, so dass $|f(x_{n})-f(x_{0})|<\epsilon$ für alle $n\geq N$ erfüllt ist. Wir kennen die Ungleichung $|f(x_{n})-f(x_{0})|<\epsilon$ aus der Konklusion des Epsilon-Delta-Kriteriums. Der Unterschied liegt darin, dass wir anstelle des Arguments $x$ das Folgenglied $x_{n}$ haben. Wenden wir also das Epsilon-Delta-Kriterium auf unseren speziellen Fall mit dem vorgegebenen $\epsilon$ an. Wir erhalten:

Es gibt ein $\delta >0$, so dass $|f(x_{n})-f(x_{0})|<\epsilon$ für alle Folgenglieder $x_{n}$ mit $|x_{n}-x_{0}|<\delta$ ist.

Wir kommen dem Ziel näher. Wenn ein Folgenglied $x_{n}$ die Ungleichung $|x_{n}-x_{0}|<\delta$ erfüllt, erfüllt es auch die Zielungleichung $|f(x_{n})-f(x_{0})|<\epsilon$. Nun wissen wir wegen $\lim _{n\to \infty }x_{n}=x_{0}$, dass $|x_{n}-x_{0}|$ beliebig klein wird. Damit gibt es ein ${\tilde {N}}\in \mathbb {N}$, so dass $|x_{n}-x_{0}|<\delta$ für alle $n\geq {\tilde {N}}$ erfüllt ist. Dieses ${\tilde {N}}$ können wir als unser $N$ wählen. Ist nämlich $n\geq N={\tilde {N}}$, so ist $|x_{n}-x_{0}|<\delta$ und damit $|f(x_{n})-f(x_{0})|<\epsilon$ nach dem Epsilon-Delta-Kriterium.

Beweis (Das Epsilon-Delta-Kriterium impliziert das Folgenkriterium)

Sei $f:D\to \mathbb {R}$ eine Funktion, die an der Stelle $x_{0}\in D$ das Epsilon-Delta-Kriterium erfüllt. Sei $(x_{n})_{n\in \mathbb {N} }$ eine Folge mit $x_{n}\in D$ für alle $n\in \mathbb {N}$ und $\lim _{n\to \infty }x_{n}=x_{0}$. Wir wollen zeigen, dass für beliebiges $\epsilon >0$ ein $N\in \mathbb {N}$ existiert, sodass $|f(x_{n})-f(x_{0})|<\epsilon$ für alle $n\geq N$ gilt.

Sei $\epsilon >0$ beliebig. Nach dem Epsilon-Delta-Kriterium gibt es ein $\delta >0$, sodass $|f(x)-f(x_{0})|<\epsilon$ für alle $x\in D$ mit $|x-x_{0}|<\delta$ ist. Wegen der Konvergenz von $(x_{n})_{n\in \mathbb {N} }$ gegen $x_{0}$ können wir ein $N\in \mathbb {N}$ finden, sodass $|x_{n}-x_{0}|<\delta$ für alle $n\geq N$ ist.

Sei $n\geq N$ beliebig. Es ist damit $|x_{n}-x_{0}|<\delta$. Nach dem Epsilon-Delta-Kriterium gilt damit $|f(x_{n})-f(x_{0})|<\epsilon$. Dies beweist $\lim _{n\to \infty }f(x_{n})=f(x_{0})$ und damit das Folgenkriterium.

Folgenkriterium impliziert Epsilon-Delta-Kriterium

Satz (Das Folgenkriterium impliziert das Epsilon-Delta-Kriterium)

Sei $f:D\to \mathbb {R}$ mit $D\subseteq \mathbb {R}$ eine Funktion. Wenn $f$ an der Stelle $x_{0}\in D$ das Folgenkriterium erfüllt, erfüllt sie auch das Epsilon-Delta-Kriterium.

Wie kommt man auf den Beweis? (Das Folgenkriterium impliziert das Epsilon-Delta-Kriterium)

Wir müssen folgende Implikation beweisen:

$f{\text{ erfüllt Folgenkriterium in }}x_{0}\in D\implies f{\text{ erfüllt Epsilon-Delta-kriterium in }}x_{0}\in D$

Wir beweisen diese Implikation über Kontraposition. Wir werden also zeigen, dass folgende Implikation gilt:

$\neg \left(f{\text{ erfüllt Epsilon-Delta-Kriterium in }}x_{0}\in D\right)\implies \neg \left(f{\text{ erfüllt Folgenkriterium in }}x_{0}\in D\right)$

Also:

$f{\text{ erfüllt nicht das Epsilon-Delta-kriterium in }}x_{0}\in D\implies f{\text{ erfüllt nicht das Folgenkriterium in }}x_{0}\in D$

Sei also $f:D\to \mathbb {R}$ eine Funktion, die das Epsilon-Delta-Kriterium an der Stelle $x_{0}\in D$ nicht erfüllt. Damit erfüllt $f$ die Unstetigkeitsversion des Epsilon-Delta-Kriteriums an der Stelle $x_{0}$. Es existiert ein $\epsilon >0$, so dass es für jedes $\delta >0$ ein $x\in D$ mit $|x-x_{0}|<\delta$ und $|f(x)-f(x_{0})|\geq \epsilon$ gibt. Wir müssen nun zeigen, dass das Folgenkriterium nicht erfüllt ist. Hierzu müssen wir eine Folge $(x_{n})_{n\in \mathbb {N} }$ von Argumenten finden, so dass $\lim _{n\to \infty }x_{n}=x_{0}$ und $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$ ist.

Um die gesuchte Folge $(x_{n})_{n\in \mathbb {N} }$ zu finden, müssen wir die Unstetigkeitsversion des Epsilon-Delta-Kriteriums geschickt nutzen. Hier wird uns ein $\epsilon >0$ vorgegeben, so dass für gewisse Argumente $x$ die Ungleichung $|f(x)-f(x_{0})|\geq \epsilon$ gilt. Wenn wir als Folgenglieder nur solche Argumente $x$ verwenden, dann ist automatisch wegen dieser Ungleichung $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$.

Nun brauchen wir eine Argumentenfolge $(x_{n})_{n\in \mathbb {N} }$, die gegen $x_{0}$ konvergiert. Hierzu suchen wir uns eine Nullfolge $(\delta _{n})_{n\in \mathbb {N} }$. Bespielsweise kann $\delta _{n}={\tfrac {1}{n}}$ gewählt werden. Für jedes $\delta _{n}$ finden wir ein Argument $x_{n}$ mit $|x_{n}-x_{0}|<\delta _{n}$ und $|f(x_{n})-f(x_{0})|\geq \epsilon$. Aus diesen $x_{n}$ bilden wir die gesuchte Argumentenfolge $(x_{n})_{n\in \mathbb {N} }$. Diese erfüllt zum einen $|x_{n}-x_{0}|<\delta _{n}$ und wegen $\lim _{n\to \infty }\delta _{n}=0$ damit $\lim _{n\to \infty }x_{n}=x_{0}$. Zum anderen kann wegen $|f(x_{n})-f(x_{0})|\geq \epsilon$ die Funktionswertfolge $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ nicht gegen $f(x_{0})$ konvergieren.

Beweis (Das Folgenkriterium impliziert das Epsilon-Delta-Kriterium)

Wir beweisen den Satz über Kontraposition. Hierzu müssen wir zeigen, dass eine Funktion $f:D\to \mathbb {R}$, die das Epsilon-Delta-Kriterium an der Stelle $x_{0}\in D$ nicht erfüllt, auch das Folgenkriterium an der Stelle $x_{0}$ nicht erfüllt. Sei also $f:D\to \mathbb {R}$ mit $D\subseteq \mathbb {R}$ eine Funktion, die an der Stelle $x_{0}\in D$ das Epsilon-Delta-Kriterium nicht erfüllt. Es gibt also ein $\epsilon >0$, so dass für alle $\delta >0$ ein $x\in D$ mit $|x-x_{0}|<\delta$ und $|f(x)-f(x_{0})|\geq \epsilon$ existiert.

Für jedes $\delta _{n}={\tfrac {1}{n}}$ gibt es damit ein $x_{n}\in D$ mit $|x_{n}-x_{0}|<\delta _{n}$ und $|f(x_{n})-f(x_{0})|\geq \epsilon$. Aus der Ungleichung $|x_{n}-x_{0}|<\delta _{n}$ folgt $x_{0}-\delta _{n}\leq x_{n}\leq x_{0}+\delta _{n}$. Da $\lim _{n\to \infty }\delta _{n}=0$ ist, ist sowohl $\lim _{n\to \infty }x_{0}-\delta _{n}=x_{0}$ als auch $\lim _{n\to \infty }x_{0}+\delta _{n}=x_{0}$. Nach dem Sandwichsatz konvergiert damit die Folge $(x_{n})_{n\in \mathbb {N} }$ gegen $x_{0}$.

Jedoch kann wegen $|f(x_{n})-f(x_{0})|\geq \epsilon$ für alle $n\in \mathbb {N}$ die Folge $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ nicht gegen $f(x_{0})$ konvergieren. Damit ist das Folgenkriterium an der Stelle $x_{0}$ für die Funktion $f$ nicht erfüllt. Es gibt nämlich eine Argumentenfolge $(x_{n})_{n\in \mathbb {N} }$ mit $\lim _{n\to \infty }x_{n}=x_{0}$ und $\lim _{n\to \infty }f(x_{n})\neq f(x_{0})$.

Übungsaufgaben

Stetigkeit der Betragsfunktion

Aufgabe (Stetigkeit der Betragsfunktion)

Beweise die Stetigkeit der Betragsfunktion.

Beweis (Stetigkeit der Betragsfunktion)

Sei $f:\mathbb {R} \to \mathbb {R}$ mit $f(x)=|x|$ die Betragsfunktion. Sei $x_{0}\in \mathbb {R}$ eine beliebige Zahl und sei $(x_{n})_{n\in \mathbb {N} }$ eine Folge reeller Zahlen mit $\lim _{n\to \infty }x_{n}=x_{0}$. Im Kapitel „Grenzwertsätze: Grenzwert von Folgen berechnen“ haben wir die Betragsregel bewiesen. Diese besagt, dass $\lim _{n\to \infty }|x_{n}|=|x_{0}|$ ist, wenn $\lim _{n\to \infty }x_{n}=x_{0}$ ist. Also haben wir:

$\lim _{n\to \infty }f(x_{n})=\lim _{n\to \infty }|x_{n}|=|x_{0}|=f(x_{0})$

Dies beweist die Stetigkeit von $f$ nach dem Folgenkriterium.

Unstetigkeit der topologischen Sinusfunktion

Beweis der Unstetigkeit der topologischen Sinusfunktion mit Hilfe des Folgenkriteriums

Aufgabe (Unstetigkeit der topologischen Sinusfunktion)

Beweise die Unstetigkeit der folgenden Funktion:

$f:\mathbb {R} \to \mathbb {R} :x\mapsto {\begin{cases}\sin \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0\end{cases}}$

Wie kommt man auf den Beweis? (Unstetigkeit der topologischen Sinusfunktion)

Damit $f$ eine unstetige Funktion ist, muss sie mindestens eine Unstetigkeitkeitsstelle besitzen. Für jedes $x\neq 0$ entspricht $f$ in einer hinreichend kleinen Umgebung von $x$ der Funktion $\sin \left({\tfrac {1}{x}}\right)$. Da die Funktion $\sin \left({\tfrac {1}{x}}\right)$ als Komposition stetiger Funktionen stetig ist, muss auch $f$ für alle $x\neq 0$ stetig sein. Damit muss die Unstetigkeitsstelle bei $x=0$ liegen.

Um mit dem Folgenkriterium zu zeigen, dass $f$ an der Stelle $x=0$ unstetig ist, müssen wir eine Argumentenfolge $(x_{n})_{n\in \mathbb {N} }$ mit $\lim _{n\to \infty }x_{n}=0$ und $\lim _{n\to \infty }f(x_{n})\neq f(0)$ finden. Um diese Argumentenfolge zu finden, schauen wir uns zunächst den Graphen der Funktion $f$ an:

Graph der topologischen Sinusfunktion f

In der Graphik sehen wir, dass die Funktion $f$ in jeder Umgebung des Nullpunkts jeden Wert zwischen $-1$ und $1$ beliebig oft annimmt. Also können wir $(x_{n})_{n\in \mathbb {N} }$ so wählen, dass $f(x_{n})$ immer gleich $1$ ist. Dann ist nämlich garantiert, dass $\lim _{n\to \infty }f(x_{n})=1\neq 0=f(0)$ ist. Dabei wählen wir $x_{n}$ so, dass $x_{n}$ von oben gegen Null konvergiert.

In der folgenden Graphik sind neben dem Graphen von $f$ auch die Funktionswerte der Folge $x_{n}$ eingetragen. Man sieht, dass für $x_{n}\to 0$ die Funktionswerte gegen $1$ konvergieren, was ungleich dem Funktionswert $f(0)=0$ ist:

Graph der topologischen Sinusfunktion f zusammen mit den Funktionswerten derjenigen Argumentenfolge, die von rechts gegen 0 geht und deren Bilder stets 1 sind.

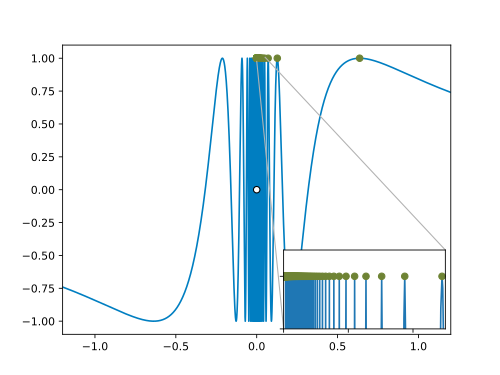
Wie lauten die Werte für $x_{n}$? Formen wir hierzu die Gleichung $f(x)=1$ nach $x$ um:

${\begin{aligned}{\begin{array}{rrrl}&&f(x)&=1\\[0.5em]{\overset {f(0)\neq 0}{\iff {}}}&&\sin \left({\frac {1}{x}}\right)&=1\\[0.5em]\iff {}&\exists k\in \mathbb {Z} :&{\frac {1}{x}}&={\frac {\pi }{2}}+2k\pi \\[0.5em]\iff {}&\exists k\in \mathbb {Z} :&x&={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\end{array}}\end{aligned}}$

Für alle $x={\tfrac {1}{{\frac {\pi }{2}}+2k\pi }}$ mit $k\in \mathbb {Z}$ gilt also $f(x)=1$. Damit unsere Argumente $x_{n}$ positiv sind und von oben gegen Null konvergieren, wählen wir $x_{n}={\tfrac {1}{{\frac {\pi }{2}}+2n\pi }}$. Es gilt dann:

$\lim _{n\to \infty }x_{n}=\lim _{n\to \infty }{\frac {1}{{\frac {\pi }{2}}+2n\pi }}=0$

Jedoch haben wir gesehen, dass $\lim _{n\to \infty }f(x_{n})=1\neq 0=f(0)$ ist. Wir haben also eine Argumentenfolge $(x_{n})_{n\in \mathbb {N} }$ gefunden, welche die Unstetigkeit von $f$ an der Stelle $x=0$ beweist.

Beweis (Unstetigkeit der topologischen Sinusfunktion)

Sei $f:\mathbb {R} \to \mathbb {R}$ mit $f(x)=\sin \left({\tfrac {1}{x}}\right)$ für $x\neq 0$ und $f(0)=0$. Wir betrachten die Folge $(x_{n})_{n\in \mathbb {N} }$ mit $x_{n}={\tfrac {1}{{\frac {\pi }{2}}+2n\pi }}$. Für diese Folge ist:

$\lim _{n\to \infty }x_{n}=\lim _{n\to \infty }{\frac {1}{{\frac {\pi }{2}}+2n\pi }}=0$

Außerdem gilt:

${\begin{aligned}\lim _{n\to \infty }f(x_{n})&=\lim _{n\to \infty }f\left({\frac {1}{{\frac {\pi }{2}}+2n\pi }}\right)\\[0.5em]&=\lim _{n\to \infty }\sin \left({\frac {1}{\frac {1}{{\frac {\pi }{2}}+2n\pi }}}\right)\\[0.5em]&=\lim _{n\to \infty }\sin \left({\frac {\pi }{2}}+2n\pi \right)\\[0.5em]&=\lim _{n\to \infty }1=1\end{aligned}}$

Damit ist $\lim _{n\to \infty }f(x_{n})=1\neq 0=f(0)$, obwohl $\lim _{n\to \infty }x_{n}=0$ ist. Dies beweist, dass $f$ an der Stelle $x=0$ und somit auch insgesamt unstetig ist.