Zwischenwertsatz – Serlo „Mathe für Nicht-Freaks“
Der Zwischenwertsatz besagt, dass jede stetige Funktion alle Werte zwischen und mindestens einmal annimmt. Stetige Funktionen nehmen also alle Zwischenwerte zwischen und an (wenn es zwischen und keine Lücken im Definitionsbereich gibt). Der Zwischenwertsatz kann somit genutzt werden, um die Existenz von Funktionswerten zu beweisen.
Motivation
[Bearbeiten]Sei eine beliebige stetige Funktion. An der Stelle besitzt sie den Funktionswert und an der Stelle den Funktionswert . Nehmen wir an, dass ist. Sei außerdem ein beliebiger Wert zwischen und , also :

Nach unserer Vorstellung besitzen stetige Funktionen innerhalb des Definitionsbereichs keine Sprünge. Da auf dem gesamten Intervall definiert ist und somit ihr Definitionsbereich zusammenhängend ist, verbindet der Graph die Punkte und ohne Sprünge. Wenn wir und ohne Absetzen des Stifts verbinden, müssen wir irgendwann die Gerade kreuzen. Es gibt also mindestens einen Schnittpunkt zwischen der Geraden und dem Graphen von :

Für die -Werte der Schnittpunkte gilt . Der Zwischenwert wird also mindestens einmal durch die Funktion angenommen. Wir haben intuitiv gesehen, dass stetige Funktionen alle Werte zwischen zwei Funktionswerten mindestens einmal annehmen, wenn der Definitionsbereich keine Lücken zwischen den beiden Argumenten besitzt.
Der Zwischenwertsatz
[Bearbeiten]Satz (Zwischenwertsatz)
Sei eine stetige Funktion mit und . Sei ein Wert zwischen den beiden Funktionswerten und . Es gilt also oder . Dann gibt es mindestens eine reelle Zahl mit . Der Zwischenwert wird also mindestens einmal von der Funktion angenommen.
Nullstellensatz von Bolzano
[Bearbeiten]Für den Beweis des Zwischenwertsatzes reicht es aus, diesen nur für den Spezialfall zu beweisen. Dieser Spezialfall wird auch „Nullstellensatz von Bolzano” genannt:
Satz (Nullstellensatz von Bolzano)
Sei eine stetige Funktion mit und . Sei außerdem die Null ein Zwischenwert von und , also oder . Dann besitzt mindestens eine Nullstelle. Es gibt also mindestens ein Argument mit .
Wieso reicht es, nur diesen Spezialfall zu betrachten? Nehmen wir eine stetige Funktion und einen Wert zwischen den Funktionswerten und . Nach dem Zwischenwertsatz müssen wir nun ein mit finden. Nun gilt:
Damit ist genau dann , wenn ist. Wir definieren nun die Hilfsfunktion mit . Wie wir gerade festgestellt haben, ist genau im Fall die Gleichung erfüllt. Wenn wir also eine Nullstelle von finden, dann nimmt auch die Funktion den Wert an.
Nun erfüllt die Funktion alle Voraussetzungen des Nullstellensatz von Bolzano. Es ist eine Funktion der Form mit dem abgeschlossenen Intervall als Definitionsbereich. Als Verkettung stetiger Funktionen ist die Funktion stetig. Im Fall ist:
Damit folgt aus die Ungleichungskette . Betrachten wir nun den Fall :
Es folgt insgesamt, dass Null ein Zwischenwert von und ist. Somit erfüllt die Voraussetzungen des Nullstellensatz von Bolzano. Nach diesem Nullstellensatz gibt es ein mit . Für dieses ist dann . Dies zeigt, dass aus dem Nullstellensatz von Bolzano der allgemeinere Zwischenwertsatz folgt. Wir müssen also nur den Nullstellensatz von Bolzano beweisen.
Beweis des Nullstellensatz von Bolzano
[Bearbeiten]Beweis (Nullstellensatz von Bolzano)
Sei eine stetige Funktion mit oder . Im Folgenden betrachten wir den Fall . Der andere Fall kann analog bewiesen werden. Wir müssen nun eine Nullstelle von finden. Dies kann durch eine geeignete Intervallschachtelung gezeigt werden. Als Startintervall wählen wir , also und . Wir wissen nämlich, dass sich im Intervall die gesuchte Nullstelle befinden muss.
Für oder haben wir bereits eine Nullstelle bei bzw. gefunden und sind fertig. Falls und ist, verkleinern wir unser Intervall. Wir betrachten hierzu den Mittelpunkt des Startintervalls. Ist der Wert von an diesem Punkt gleich Null, so haben wir wieder eine Nullstelle gefunden und sind fertig.
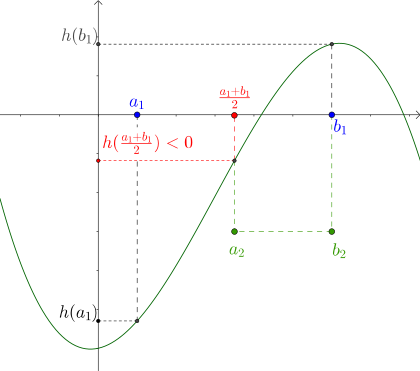
Wenn ist, so wählen wir nun ein anderes Intervall, in dem sich eine Nullstelle befinden muss. Nehmen wir an, es sei . Dann ergibt sich folgendes Bild:

Wir sehen, dass der Graph im ersten Intervall von bis die -Achse überqueren muss. Da als stetige Funktion keine Sprünge aufweist und in diesem Intervall keine Definitionslücken aufweist, sollte sich in diesem Intervall also eine Nullstelle von befinden. Da beide Funktionswerte und positiv sind, können wir nicht sagen, ob sich im Bereich von bis eine Nullstelle befindet oder nicht. Deswegen wählen wir als zweites Intervall .
Wenn demgegenüber kleiner als Null ist, muss der Graph von im zweiten Intervall von bis einen Vorzeichenwechsel vollführen. Dementsprechend sollte sich dort eine Nullstelle befinden und wir wählen in diesem Fall als zweites Intervall :
Insgesamt bestimmen wir folgendermaßen:
Diesen Vorgang wiederholen wir nun immer wieder: Im -ten Schritt berechnet wir den Mittelpunkt des Intervalls . Nimmt hier den Wert an, sind wir fertig und können als Nullstelle zurückgeben. Ansonsten wählen wir analog zu vorher ein neues Intervall mit folgender Definition
Durch dieses Vorgehen erhalten wir entweder nach irgendeinem Schritt eine gesuchte Nullstelle, oder wir bekommen eine Folge von Intervallen . So wie wir die Folgenglieder gewählt haben, ist die Folge monoton wachsend, und die Folge monoton fallend. Da jedes Folgenglied im Intervall liegt, sind die Folgen auch beschränkt. Daraus können wir nach dem Monotoniekriterium für Folgen folgern, dass beide Folgen konvergieren. Beachte, dass die Länge des Intervalls bei jedem Schritt halbiert wird. Das heißt:
Und damit folgt: . Damit konvergieren die Folgen der unteren bzw. oberen Intervallgrenzen gegen den gleichen Wert . Außerdem gilt mit unserer Wahl, dass sowie für alle gilt. Deswegen gilt für die Grenzwerte: und . Weil stetig ist, gilt
Mit der oberen Zeile folgt also und , damit muss gelten und wir haben auch in diesem Fall eine Nullstelle der Funktion gefunden.
Folgerungungen aus dem Zwischenwertsatz
[Bearbeiten]Stetige Funktionen bilden Intervalle auf Intervalle ab
[Bearbeiten]Mit Hilfe des Zwischenwertsatzes können wir beweisen, dass stetige Funktionen Intervalle auf Intervalle abbilden:
Satz (Folgerung aus Zwischenwertsatz)
Sei ein Intervall und stetig. Dann ist auch ein Intervall.
Beweis (Folgerung aus Zwischenwertsatz)
Wir setzen und . Dabei erlauben wir (wenn nach unten unbeschränkt ist) und (wenn nach oben unbeschränkt ist). Nehmen wir nun eine reelle Zahl mit . Aus der Definition vom Infimum folgt aus , dass es ein mit gibt. Analog gibt es ein mit . Ingesamt ist damit .
ist damit ein Zwischenwert zweier Funktionswerte von . Da stetig ist, gibt es nach dem Zwischenwertsatz ein mit . Da beliebig war, folgt . Nun können noch oder Elemente von sein. Damit muss eines der folgenden vier Intervalle sein:
Wir sehen, dass ein Intervall ist.
Wertebereich von Potenzfunktionen
[Bearbeiten]Beispiel (Wertebereich der Potenzfunktionen )
Die Potenzfunktionen mit für sind stetig. Weiter gilt
Damit ist . Außerdem ist
Bei ungeraden ist . Für gerade ist , denn für alle ist und die Null wird wegen angenommen. Nach dem Zwischenwertsatz ist damit
Wertebereich der Exponentialfunktion
[Bearbeiten]Beispiel (Wertebereich der Exponentialfunktion)
Die Exponentialfunktion ist stetig. Außerdem gilt für alle . Es ist und . Es ist damit und . Da weder noch durch die Exponentialfunktion angenommen werden, folgt aus dem Zwischenwertsatz
Aufgabe (Wertebereich der verallgemeinerten Exponentialfunktion)
Für definiert
die verallgemeinerte Exponentialfunktion. Zeige: .
Hinweis: Unterscheide die Fälle und .
Lösung (Wertebereich der verallgemeinerten Exponentialfunktion)
Da und stetig auf stetig sind, ist auch als Komposition dieser Funktionen stetig auf . Weiter ist , da ist.
Fall 1:
Hier gilt , und damit ist . Daraus folgt . Andererseits ist , und somit . Insgesamt ergibt sich in diesem Fall .
Fall 2:
Hier ist , und daher . Also folgt . Andererseits gilt , und somit . Also gilt auch sich diesem Fall .
Übungsaufgabe: Fixpunktsatz
[Bearbeiten]Beweis eines Fixpunktsatzes
[Bearbeiten]In der folgenden Aufgabe beweisen wir einen Fixpunktsatz. Fixpunkte sind Argumente einer Funktion , die die Gleichung erfüllt. Fixpunkte werden also durch eine Funktion nicht verändert. Fixpunktsätze sind wiederum Sätze, die die Existenz von Fixpunkten in gewissen Situationen beweisen. Für die Mathematik sind solche Sätze wichtig, weil manchmal die Existenz eines Objekts auf die Existenz eines Fixpunktes zurückgeführt werden kann. Beispielsweise ist das Argument genau dann Nullstelle einer Funktion , wenn die Funktion mit der Zuordnungsvorschrift einen Fixpunkt besitzt. Aus der Existenz eines Fixpunkts der Funktion , folgt die Existenz einer Nullstelle für . In der folgenden Aufgabe werden wir einen Zwischenwertsatz beweisen:
Aufgabe (Fixpunktsatz)
Sei eine stetige Funktion. Beweise, dass mindestens einen Fixpunkt besitzt. Fixpunkte sind Stellen mit .
Wie kommt man auf den Beweis? (Fixpunktsatz)
Durch Umstellung der Gleichung erhalten wir . Damit ist genau dann ein Fixpunkt von , wenn eine Nullstelle der Funktion ist. Definieren also die Hilfsfunktion mit . Wie sich herausstellt, können wir den Nullstellensatz von Bolzano einsetzen, um die Existenz einer Nullstelle zu beweisen. Hierfür müssen wir die Voraussetzungen dieses Satzes beweisen:
- ist stetig.
- Null ist ein Zwischenwert von und .
ist stetig als Verknüpfung stetiger Funktionen und wir können außerdem beweisen, dass ist. Der Nullstellensatz liefert damit die Existenz des Grenzwerts.
Beweis (Fixpunktsatz)
Sei eine stetige Funktion. Wir definieren die Hilfsfunktion . Für diese gilt:
- ist stetig auf als Differenz der stetigen Funktionen und .
- Es ist , weil:
- .
Damit erfüllt die Voraussetzungen des Nullstellensatzes. Es gibt daher ein mit . Es folgt . Also besitzt einen Fixpunkt.
Voraussetzungen zum Fixpunktsatz
[Bearbeiten]Im obigen Fixpunktsatz ist die Stetigkeit eine notwendige Voraussetzung des bewiesenen Fixpunktsatzes. Wenn wir diese weglassen, finden wir eine Funktion , für die der Fixpunktsatz nicht mehr gilt. Dies zeigt folgende Aufgabe:
Aufgabe (Fixpunktsatz)
Gib eine Funktion mit für alle an.
Beweis (Fixpunktsatz)
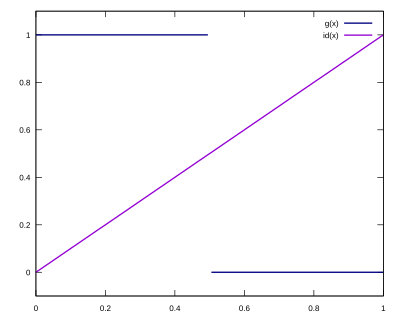
Zum Beispiel besitzt die Funktion
keinen Fixpunkt. Dies zeigt der folgende Graph der Funktion . Es gibt nämlich keinen Schnittpunkt des Graphen von mit dem Graphen der Identitätsfunktion :
Übungsaufgabe: Nullstellen und Wertebereich von Polynomen
[Bearbeiten]Nullstellen von Polynomen
[Bearbeiten]Die folgende Aufgabe stellt einen Spezialfall des Fundamentalsatzes der Algebra dar. Dieser besagt, dass eine nicht-konstante Polynomfunktion
mit komplexen Koeffizienten mindestens eine komplexe Nullstelle hat. Im Reellen stimmt diese Aussage im Allgemeinen nicht. Ein Polynom mit reellen Koeffizienten muss keine reelle Nullstelle haben. Eine Polynomfunktion ohne reelle Nullstellen ist zum Beispiel . Für gewisse Polynome können wir jedoch die Existenz einer Nullstelle beweisen:
Aufgabe (Nullstellen von Polynomen)
Sei
eine Polynomfunktion mit und . Wenn , also der Grad von , ungerade ist, besitzt mindestens eine Nullstelle.
Zusammenfassung des Beweises (Nullstellen von Polynomen)
Wir werden die Aufgabe mit Hilfe des Nullstellensatzes beweisen. Hierzu müssen wir zwei reelle Zahlen mit oder finden. Dies folgt nun aus und , was wir mit einem einfachen Umformungstrick für den Fall zeigen können. Wir werden nur den Fall ausführlich behandeln. Der Fall kann analog geführt werden.
Lösung (Nullstellen von Polynomen)
Wir führen den Beweis für . Im Fall kann analog der Satz bewiesen werden. Für erhalten wir durch Ausklammern von :
Der Ausdruck in den Klammern konvergiert für gegen . Dies gilt, da die Terme für gegen konvergieren. Da ungerade ist, folgt:
und
Damit muss es aber mit geben. Weiter ist als Polynomfunktion stetig als Komposition der stetigen Funktionen für . Aus dem Nullstellensatz von Bolzano folgt, dass es ein mit gibt. Die Polynomfunktion hat also mindestens eine Nullstelle.
Wertebereich von Polynomen
[Bearbeiten]Aufgabe (Wertebereich von Polynomen)
Sei
eine Polynomfunktion mit und , und ungerade. Zeige, dass .
Lösung (Wertebereich von Polynomen)
Fall 1:
Für ist:
und
Da stetig ist, folgt .
Fall 2:
Analog zum ersten Fall.
Übungsaufgabe: Existenz von Wurzeln
[Bearbeiten]Der Zwischenwertsatz bietet eine weitere Möglichkeit die Existenz von Wurzeln zu beweisen. Im Kapitel „Wurzel reeller Zahlen“ haben wir dies bereits mit Hilfe einer Intervallschachtellung bewiesen. Wir werden nun einen alternativen Beweis mit Hilfe des Zwischenwertsatzes kennen lernen. Zur Erinnerung: Die -te Wurzel für eine positive Zahl ist eine positive reelle Zahl mit .
Aufgabe (Existenz der Wurzel)
Sei . Zeige, dass es für alle eine positive reelle Zahl mit gibt.
Lösung (Existenz der Wurzel)
Es ist genau dann , wenn ist. Die gesuchte Zahl muss also eine positive Nullstelle des Polynoms mit sein. Zunächst ist als Polynom auf ganz stetig. Damit ist auch auf den Intervall stetig. Weiter gilt
sowie
Damit ist . Nach dem Zwischenwertsatz besitzt im Intervall mindestens eine Nullstelle. Weil alle Zahlen aus positiv sind, ist auch die Nullstelle positiv. Außerdem erfüllt sie die Gleichung .
Übungsaufgabe: Lösung einer Gleichung
[Bearbeiten]Der Zwischenwert- beziehungsweise Nullstellensatz kann verwendet werden, die Existenz einer Lösung für eine Gleichung zu begründen. Hier wird aus der Gleichung eine stetige Funktion gebildet, auf die der Zwischenwert- beziehungsweise der Nullstellensatz angewandt werden kann.
Aufgabe (Lösung einer Gleichung)
Zeige, dass es genau ein mit gibt.
Lösung (Lösung einer Gleichung)

Beweisschritt: Die Gleichung besitzt eine Lösung
Wir bilden die Hilfsfunktion
Diese ist stetig, als Differenz der stetigen Funktionen und . Weiter gilt
sowie
Nach dem Nullstellensatz gibt es also ein mit . Für dieses gilt dann . Es löst also unsere Gleichung.
Beweisschritt: Es gibt genau eine Lösung der Gleichung
Wir unterscheiden vier Fälle
Fall 1:
Es ist . Damit gibt es kein mit geben.
Fall 2:
Es ist . Also kann es kein mit geben.
Fall 3:
Oben haben wir bereits gezeigt, dass es ein mit gibt. Nun ist streng monoton steigend für streng monoton fallend. Also kann es kein weiteres mit geben.
Fall 4:
Es ist . Also kann es kein mit geben.
Aus beiden Beweisschritten folgt, dass es genau ein mit gibt.



![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)








![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)









![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)


![{\displaystyle h:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1833b6178fc06e33367b794d4c27d8f9e1a9f36e)





![{\displaystyle {\tilde {x}}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7a70e57f199d3304bbe0964d741eeafd3ee2e32)





![{\displaystyle [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/641f4ab7608607e1e61bd1958d0b9da424be1752)
![{\displaystyle {\begin{aligned}f(a)\leq s\iff f(a)-s\leq 0\iff h(a)\leq 0\\[0.3em]f(b)\geq s\iff f(b)-s\geq 0\iff h(b)\geq 0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbaa2c8f353583041cc79a845c2fce48304cd40f)

![{\displaystyle {\begin{aligned}f(a)\geq s\iff f(a)-s\geq 0\iff h(a)\geq 0\\[0.3em]f(b)\leq s\iff f(b)-s\leq 0\iff h(b)\leq 0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/633ae0786835624a0891771c2885ee58ad0c68ab)
![{\displaystyle [a_{1},b_{1}]=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad3ba71c5021f6b79dc6acd9fdb655f20a633ba5)















![{\displaystyle [a_{2},b_{2}]=\left[a_{1},{\tfrac {a_{1}+b_{1}}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e514878526ae4dc87f68106e20b7d8cdc453a2e)
![{\displaystyle \left[{\tfrac {a_{1}+b_{1}}{2}},b_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8c24ad014b725551415179361689d06261c22ea)
![{\displaystyle [a_{2},b_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2cae95a31bf77847185496288d80966494407a6)
![{\displaystyle [a_{2},b_{2}]={\begin{cases}\left[a_{1},{\frac {a_{1}+b_{1}}{2}}\right]&;h\left({\frac {a_{1}+b_{1}}{2}}\right)>0\\\left[{\frac {a_{1}+b_{1}}{2}},b_{1}\right]&;h\left({\frac {a_{1}+b_{1}}{2}}\right)<0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34e9af43757190a432b206673de3a2ca51e89629)


![{\displaystyle [a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e30ce1f218c7164247ad32fbbcde76c02c817bd1)

![{\displaystyle [a_{n+1},b_{n+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4218a0524695e40f6c164b3aa6f0ceeda8e0f4c2)
![{\displaystyle [a_{n+1},b_{n+1}]={\begin{cases}\left[a_{n},{\frac {a_{n}+b_{n}}{2}}\right]&;h\left({\frac {a_{n}+b_{n}}{2}}\right)>0\\\left[{\frac {a_{n}+b_{n}}{2}},b_{n}\right]&;h\left({\frac {a_{n}+b_{n}}{2}}\right)<0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a492f4ed071893d6d0f36cd21d63c6ae16546956)

![{\displaystyle ([a_{n},b_{n}])_{n\in \mathbb {N} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46a01f7a0639bafdbc58ce4b0f3f4975a6e60949)


![{\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }{(b_{n}-a_{n})}&=\lim _{n\rightarrow \infty }{{\frac {1}{2}}\cdot (b_{n-1}-a_{n-1})}\\[0.3em]&=\lim _{n\rightarrow \infty }{{\frac {1}{2}}\cdot {\frac {1}{2}}\cdot (b_{n-2}-a_{n-2})}\\[0.3em]&\vdots \\[0.3em]&=\lim _{n\rightarrow \infty }{{\frac {1}{2^{n}}}\cdot (b_{1}-a_{1})}=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b956430d61cacbc7c3997e375c83ae25f0af297)

![{\displaystyle c\in [a;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02b8df5ba00bbc02820be401c0dbc93d73392da8)






























![{\displaystyle {\begin{aligned}f(I)={\begin{cases}[A,B]&A{\text{ und }}B{\text{ werden von }}f{\text{ angenommen}}\\[0.5em][A,B)&A{\text{ wird von }}f{\text{ angenommen, }}B{\text{ nicht}}\\[0.5em](A,B]&B{\text{ wird von }}f{\text{ angenommen, }}A{\text{ nicht}}\\[0.5em](A,B)&A{\text{ und }}B{\text{ werden von }}f{\text{ nicht angenommen}}\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfa116f9fc76e83877d45b215514612b140b3da8)















































![{\displaystyle f:[a,b]\to [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f359e29e1446d9bfea5759414f0f320db9f7796e)



![{\displaystyle h:[a,b]\to \mathbb {R} :x\mapsto h(x)=f(x)-x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/809932a2003de787ae164661a63528f3664cd8c2)
![{\displaystyle {\text{id}}:[a,b]\to [a,b]:x\mapsto x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71edd132aab83df0a40f98d7285f56893c940915)
![{\displaystyle h(a)=\underbrace {f(a)} _{\in [a,b]}-a\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c338aad1556500ef398c4e96618bf4b66628845)
![{\displaystyle h(b)=\underbrace {f(b)} _{\in [a,b]}-b\leq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/923d3af35c516619ab49d871857439aa64169a8b)


![{\displaystyle g:[a,b]\to [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d99b57dcedc3a03efd7b9652a9eec76fefc853f)
![{\displaystyle g:[0,1]\to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0329691aecddec5158ad537f5df2e83578a302e2)

![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)
![{\displaystyle g:[0,1]\to [0,1]:x\mapsto g(x)={\begin{cases}1&{\text{ für }}0\leq x\leq {\tfrac {1}{2}},\\0&{\text{ für }}{\tfrac {1}{2}}<x\leq 1\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0188a3c26bc42b9c0739a7bbd7ef3907b32ff96b)
![{\displaystyle {\text{id}}:[0,1]\to [0,1],\ x\mapsto x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5011821f7da6ec444e105635caac19e7c80534d1)



























![{\displaystyle {\sqrt[{n}]{\alpha }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/531fb33f9c467602294387d194015ce0e0e23e6d)






![{\displaystyle [0,\alpha +1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86505e10814a30d1a0fd85d6dd90b97771172234)

![{\displaystyle {\begin{aligned}p(1+\alpha )&=(1+\alpha )^{n}-\alpha \\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\text{Bernoulli-Ungleichung}}\right.}\\[0.3em]&\geq 1+n\alpha -\alpha \\&=1+\underbrace {(n-1)} _{\geq 0}\alpha \\&\geq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1aff16c08836e07bb85900e24810e35cf5a1194)




















