Mathematik Nachhilfe von Linda.
Großbuchstabe
Kleinbuchstabe
Name
A
{\displaystyle \mathrm {A} }
α
{\displaystyle \alpha }
Alpha
B
{\displaystyle \mathrm {B} }
β
{\displaystyle \beta }
Beta
Γ
{\displaystyle \Gamma }
γ
{\displaystyle \gamma }
Gamma
Δ
{\displaystyle \Delta }
δ
{\displaystyle \delta }
Delta
E
{\displaystyle \mathrm {E} }
ϵ
{\displaystyle \epsilon }
Epsilon
Z
{\displaystyle \mathrm {Z} }
ζ
{\displaystyle \zeta }
Zeta
H
{\displaystyle \mathrm {H} }
η
{\displaystyle \eta }
Eta
Θ
{\displaystyle \Theta }
ϑ
{\displaystyle \vartheta }
Theta
I
{\displaystyle \mathrm {I} }
ι
{\displaystyle \iota }
Iota
K
{\displaystyle \mathrm {K} }
κ
{\displaystyle \kappa }
Kappa
Λ
{\displaystyle \Lambda }
λ
{\displaystyle \lambda }
Lambda
M
{\displaystyle \mathrm {M} }
μ
{\displaystyle \mu }
My
N
{\displaystyle \mathrm {N} }
ν
{\displaystyle \nu }
Ny
Ξ
{\displaystyle \Xi }
ξ
{\displaystyle \xi }
Xi
O
{\displaystyle \mathrm {O} }
o
{\displaystyle \mathrm {o} }
Omikron
Π
{\displaystyle \Pi }
π
{\displaystyle \pi }
Pi
P
{\displaystyle \mathrm {P} }
ρ
{\displaystyle \rho }
Rho
Σ
{\displaystyle \Sigma }
σ
{\displaystyle \sigma }
Sigma
T
{\displaystyle \mathrm {T} }
τ
{\displaystyle \tau }
Tau
>
{\displaystyle \mathrm {>} }
υ
{\displaystyle \upsilon }
Ypsilon
Φ
{\displaystyle \Phi }
ϕ
{\displaystyle \phi }
Phi
X
{\displaystyle \mathrm {X} }
χ
{\displaystyle \chi }
Chi
Ψ
{\displaystyle \Psi }
ψ
{\displaystyle \psi }
Psi
Ω
{\displaystyle \Omega }
ω
{\displaystyle \omega }
Omega
Symbol
Bedeutung
∈
{\displaystyle \in }
ein Element von
∉
{\displaystyle \notin }
kein Element von
⊂
{\displaystyle \subset }
Teilmenge von
⫅
{\displaystyle \subseteqq }
Teilmenge oder gleiche Menge
∪
{\displaystyle \cup }
vereinigt mit
⋃
i
=
1
n
{\displaystyle \bigcup _{i=1}^{n}}
Vereinigung von Mengen
∩
{\displaystyle \cap }
geschnitten mit
⋂
i
=
1
n
{\displaystyle \bigcap _{i=1}^{n}}
Schnitt von Mengen
∖
{\displaystyle \setminus }
ohne bzw. Differenzmenge
∅
{\displaystyle \varnothing }
leere Menge
{
}
{\displaystyle \{\}}
leere Menge
L
{\displaystyle \mathbb {L} }
Lösungsmenge
G
{\displaystyle \mathbb {G} }
Grundmenge
N
{\displaystyle \mathbb {N} }
Menge der natürlichen Zahlen
{
1
,
2
,
.
.
.
}
{\displaystyle \{1,2,...\}}
N
0
{\displaystyle \mathbb {N} _{0}}
Menge der natürliche Zahlen inklusive Null
{
0
,
1
,
2
,
.
.
.
}
{\displaystyle \{0,1,2,...\}}
Z
{\displaystyle \mathbb {Z} }
Menge der ganzen Zahlen
{
.
.
.
,
−
2
,
−
1
,
0
,
1
,
2
,
.
.
.
}
{\displaystyle \{...,-2,-1,0,1,2,...\}}
Q
{\displaystyle \mathbb {Q} }
Menge rationalen Zahlen, bzw. Menge der Brüche
R
{\displaystyle \mathbb {R} }
Menge der reellen Zahlen
C
{\displaystyle \mathbb {C} }
Menge der komplexen Zahlen
Symbol
Bedeutung
=
{\displaystyle =}
gleich
≠
{\displaystyle \neq }
ungleich
:=
{\displaystyle :=}
definiert als
<
kleiner als
>
größer als
≤
{\displaystyle \leq }
kleiner gleich
≥
{\displaystyle \geq }
größer gleich
+
{\displaystyle +}
plus, Additionszeichen
−
{\displaystyle -}
minus, Subtraktionszeichen
⋅
{\displaystyle \cdot }
mal, Multiplikationszeichen
:
{\displaystyle :}
geteilt, Divisionszeichen
Σ
{\displaystyle \Sigma }
Summe
Π
{\displaystyle \Pi }
Produkt
a
n
{\displaystyle a^{n}}
Potenz (a=Basis, b=Exponent)
{\displaystyle {\sqrt {\text{ }}}}
Wurzel
n
{\displaystyle {\sqrt[{n}]{\text{ }}}}
n-te Wurzel
log
b
{\displaystyle \log _{b}}
Logrtithmus zur Basis b
ln
{\displaystyle \ln }
natürlicher Logarithmus (zur Basis
e
{\displaystyle e}
lg
{\displaystyle \lg }
10er Logarithmus (zur Basis 10)
l
d
{\displaystyle \mathrm {ld} }
dyadischer Logarithmus (zur Basis 2)
!
{\displaystyle !}
Fakultät (
4
!
=
4
⋅
3
⋅
2
⋅
1
=
24
{\displaystyle 4!=4\cdot 3\cdot 2\cdot 1=24}
(
n
k
)
{\displaystyle \left({\begin{matrix}n\\k\end{matrix}}\right)}
Binomialkoeffizient
n
!
(
n
−
k
)
!
k
!
{\displaystyle {\begin{matrix}{\frac {n!}{\left(n-k\right)!k!}}\end{matrix}}}
(
8
5
)
=
8
⋅
7
⋅
6
5
⋅
4
⋅
3
⋅
2
⋅
1
{\displaystyle \left({\begin{matrix}8\\5\end{matrix}}\right)={\frac {8\cdot 7\cdot 6}{5\cdot 4\cdot 3\cdot 2\cdot 1}}}
|
a
|
{\displaystyle |a|}
Betrag von a
i
{\displaystyle i}
imaginäre Einheit
j
{\displaystyle j}
imaginäre Einheit (in der Elektrotechnik)
a
¯
{\displaystyle {\overline {a}}}
konjugiert komplexe Zahl zu
a
{\displaystyle a}
a
→
⊙
b
→
{\displaystyle {\overrightarrow {a}}\odot {\overrightarrow {b}}}
skalares Produkt der Vektoren
a
→
{\displaystyle {\overrightarrow {a}}}
b
→
{\displaystyle {\overrightarrow {b}}}
(
2
1
)
⊙
(
3
4
)
=
2
⋅
3
+
1
⋅
4
=
10
{\displaystyle \left({\begin{matrix}2\\1\end{matrix}}\right)\odot \left({\begin{matrix}3\\4\end{matrix}}\right)=2\cdot 3+1\cdot 4=10}
a
→
×
b
→
{\displaystyle {\overrightarrow {a}}\times {\overrightarrow {b}}}
vektorielles Produkt der Vektoren
a
→
{\displaystyle {\overrightarrow {a}}}
b
→
{\displaystyle {\overrightarrow {b}}}
|
a
→
×
b
→
|
=
|
a
→
|
⋅
|
b
→
|
sin
(
∠
(
a
→
,
b
→
)
)
{\displaystyle \left|{\overrightarrow {a}}\times {\overrightarrow {b}}\right|=\left|{\overrightarrow {a}}\right|\cdot \left|{\overrightarrow {b}}\right|\sin \left(\angle \left({\overrightarrow {a}},{\overrightarrow {b}}\right)\right)}
|
a
→
|
{\displaystyle \left|{\overrightarrow {a}}\right|}
Länge des Vektors
a
→
{\displaystyle {\overrightarrow {a}}}
|
(
3
4
)
|
=
3
2
+
4
2
=
25
=
5
{\displaystyle \left|\left({\begin{matrix}3\\4\end{matrix}}\right)\right|={\sqrt {3^{2}+4^{2}}}={\sqrt {25}}=5}
∣
{\displaystyle \mid }
ist Teiler von z.B.
3
|
15
{\displaystyle 3|15}
∤
{\displaystyle \nmid }
kein Teiler von
(
a
i
k
)
{\displaystyle \left(a_{ik}\right)}
Matrix mit den Elementen
a
i
k
{\displaystyle a_{i}k}
|
a
i
k
|
{\displaystyle \left|a_{ik}\right|}
Determinante der Matrix
≡
mod
p
{\displaystyle \equiv \mod p}
kongruent modulo
p
{\displaystyle p}
13
≡
5
mod
4
{\displaystyle 13\equiv 5\mod 4}
Symbol
Bedeutung
∥
{\displaystyle \parallel }
parallel zu
⊥
{\displaystyle \perp }
senkrecht zu
≅
{\displaystyle \cong }
kongruent, deckungsgleich
∢
{\displaystyle \sphericalangle }
Winkel
|
∢
|
{\displaystyle \left|\sphericalangle \right|}
Größe des Winkels
Symbol
Bedeutung
=
^
{\displaystyle {\hat {=}}}
entspricht
¬
{\displaystyle \neg }
Negation, nicht
∧
{\displaystyle \wedge }
Konjunktion, und
∨
{\displaystyle \vee }
Disjunktion, oder
⇒
{\displaystyle \Rightarrow }
Implikation (wenn ..., dann ...) z.B.
A
⇒
B
{\displaystyle A\Rightarrow B}
A
{\displaystyle A}
B
{\displaystyle B}
⇔
{\displaystyle \Leftrightarrow }
Äquivalenz (genau dann , wenn ...) z.B.
A
⇔
B
{\displaystyle A\Leftrightarrow B}
A
{\displaystyle A}
B
{\displaystyle B}
x
¯
{\displaystyle {\overline {x}}}
Logische Verneinung
Begriffe aus der allgemeinen Mathematik [ Bearbeiten ] Addition
S
u
m
m
a
n
d
+
S
u
m
m
a
n
d
=
S
u
m
m
e
{\displaystyle \mathrm {Summand} +\mathrm {Summand} =\mathrm {Summe} }
Subtraktion
M
i
n
u
e
n
d
−
S
u
b
t
r
a
h
e
n
d
=
D
i
f
f
e
r
e
n
z
{\displaystyle \mathrm {Minuend} -\mathrm {Subtrahend} =\mathrm {Differenz} }
Multiplikation
M
u
l
t
i
p
l
i
k
a
t
o
r
⋅
M
u
l
t
i
p
l
i
k
a
n
d
=
P
r
o
d
u
k
t
∨
F
a
k
t
o
r
⋅
F
a
k
t
o
r
=
P
r
o
d
u
k
t
{\displaystyle {\begin{matrix}&\mathrm {Multiplikator} \cdot \mathrm {Multiplikand} &=&\mathrm {Produkt} \\\vee &\mathrm {Faktor} \cdot \mathrm {Faktor} &=&\mathrm {Produkt} \end{matrix}}}
Division
D
i
v
i
d
e
n
t
:
D
i
v
i
s
o
r
=
Q
u
o
t
i
e
n
t
∨
Z
a
¨
h
l
e
r
N
e
n
n
e
r
=
Q
u
o
t
i
e
n
t
{\displaystyle {\begin{matrix}&\mathrm {Divident} :\mathrm {Divisor} &=&\mathrm {Quotient} \\\vee &{\frac {\mathrm {Z{\ddot {a}}hler} }{\mathrm {Nenner} }}&=&\mathrm {Quotient} \end{matrix}}}
Addition
a
b
+
c
d
=
a
d
+
c
b
b
d
{\displaystyle {\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+cb}{bd}}}
Subtraktion
a
b
−
c
d
=
a
d
−
c
b
b
d
{\displaystyle {\frac {a}{b}}-{\frac {c}{d}}={\frac {ad-cb}{bd}}}
Multiplikation
a
b
⋅
c
d
=
a
c
b
d
{\displaystyle {\frac {a}{b}}\cdot {\frac {c}{d}}={\frac {ac}{bd}}}
Division
a
b
:
c
d
=
a
d
b
c
{\displaystyle {\frac {a}{b}}:{\frac {c}{d}}={\frac {ad}{bc}}}
1
k
m
=
1000
m
=
10.000
d
m
=
100.000
c
m
=
1000.000
m
m
0
,
001
k
m
=
1
m
=
10
d
m
=
100
c
m
=
1000
m
m
0
,
0001
k
m
=
0
,
1
m
=
1
d
m
=
10
c
m
=
100
m
m
0
,
00001
k
m
=
0
,
01
m
=
0
,
1
d
m
=
1
c
m
=
10
m
m
0
,
000001
k
m
=
0
,
001
m
=
0
,
01
d
m
=
0
,
1
c
m
=
1
m
m
{\displaystyle {\begin{matrix}1&\mathrm {km} =&1000&\mathrm {m} =&10.000&\mathrm {dm} =&100.000&\mathrm {cm} =&1000.000&\mathrm {mm} \\0,001&\mathrm {km} =&1&\mathrm {m} =&10&\mathrm {dm} =&100&\mathrm {cm} =&1000&\mathrm {mm} \\0,0001&\mathrm {km} =&0,1&\mathrm {m} =&1&\mathrm {dm} =&10&\mathrm {cm} =&100&\mathrm {mm} \\0,00001&\mathrm {km} =&0,01&\mathrm {m} =&0,1&\mathrm {dm} =&1&\mathrm {cm} =&10&\mathrm {mm} \\0,000001&\mathrm {km} =&0,001&\mathrm {m} =&0,01&\mathrm {dm} =&0,1&\mathrm {cm} =&1&\mathrm {mm} \end{matrix}}}
Bei Flächen werden die Umrechnungen quadriert.
Bei Volumen werden die Umrechnnugen „hoch 3“ gerechnet.
1
t
=
1000
k
g
1
k
g
=
1000
g
=
=
1
g
=
1000
m
g
{\displaystyle {\begin{matrix}1&\mathrm {t} =&1000&\mathrm {kg} &&&&&&\\&&1&\mathrm {kg} &=&1000&\mathrm {g} &=&&\\&&&&=&1&\mathrm {g} &=&1000&\mathrm {mg} \end{matrix}}}
Volumen
1
d
m
3
=
1
l
=
1000
m
l
=
1000
c
m
3
{\displaystyle 1\mathrm {dm} ^{3}=1\mathrm {l} =1000\mathrm {ml} =1000\mathrm {cm} ^{3}}
1
J
a
h
r
=
365
T
a
g
e
1
T
a
g
=
24
S
t
u
n
d
e
n
=
1
S
t
u
n
d
e
=
60
M
i
n
u
t
e
n
1
M
i
n
u
t
e
=
60
S
e
k
u
n
d
e
n
{\displaystyle {\begin{matrix}1&\mathrm {Jahr} =&365&\mathrm {Tage} &&&&&&\\&&1&\mathrm {Tag} &=&24&\mathrm {Stunden} &&&\\&&&&=&1&\mathrm {Stunde} &=&60\mathrm {Minuten} &\\&&&&&&&&1\mathrm {Minute} &=60\mathrm {Sekunden} \end{matrix}}}
1
k
m
2
=
100
h
a
1
h
a
=
100
a
=
1
a
=
100
m
2
1
m
2
=
100
d
m
2
{\displaystyle {\begin{matrix}1&\mathrm {km} ^{2}=&100&\mathrm {ha} &&&&&&\\&&1&\mathrm {ha} &=&100&\mathrm {a} &&&\\&&&&=&1&\mathrm {a} &=&100\mathrm {m} ^{2}&\\&&&&&&&&1\mathrm {m} ^{2}&=100\mathrm {dm} ^{2}\end{matrix}}}
Längen quadrieren / ins Kubik nehmen z.B.
(
1
m
)
2
=
(
10
d
m
)
2
⇔
1
2
m
2
=
10
2
d
m
2
⇔
1
m
2
=
100
d
m
2
{\displaystyle \left(1\mathrm {m} \right)^{2}=\left(10\mathrm {dm} \right)^{2}\Leftrightarrow 1^{2}\mathrm {m} ^{2}=10^{2}\mathrm {dm} ^{2}\Leftrightarrow 1\mathrm {m} ^{2}=100\mathrm {dm} ^{2}}
A
=
a
2
U
=
4
⋅
a
{\displaystyle {\begin{matrix}A&=&a^{2}\\U&=&4\cdot a\end{matrix}}}
A
=
a
⋅
b
U
=
2
⋅
a
+
2
⋅
b
=
2
⋅
(
a
+
b
)
{\displaystyle {\begin{matrix}A&=&a\cdot b\\U&=&2\cdot a+2\cdot b=2\cdot (a+b)\end{matrix}}}
A
=
c
h
2
=
1
2
⋅
c
⋅
h
U
=
a
+
b
+
c
{\displaystyle {\begin{matrix}A&=&{\frac {ch}{2}}={\frac {1}{2}}\cdot c\cdot h\\U&=&a+b+c\end{matrix}}}
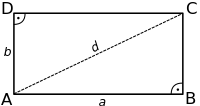
A
=
a
+
c
2
⋅
h
U
=
a
+
b
+
c
+
d
{\displaystyle {\begin{matrix}A&=&{\frac {a+c}{2}}\cdot h\\U&=&a+b+c+d\end{matrix}}}
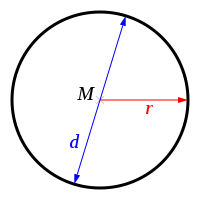
A
=
π
⋅
r
2
=
π
⋅
(
d
2
)
2
=
π
⋅
d
2
4
U
=
2
π
r
=
π
⋅
d
{\displaystyle {\begin{matrix}A&=&\pi \cdot r^{2}&=&\pi \cdot \left({\frac {d}{2}}\right)^{2}&=\pi \cdot {\frac {d^{2}}{4}}\\U&=&2\pi r&=&\pi \cdot d&\end{matrix}}}
A
=
π
r
2
⋅
α
360
∘
U
=
π
r
⋅
α
180
{\displaystyle {\begin{matrix}A&=&\pi r^{2}\cdot {\frac {\alpha }{360^{\circ }}}\\U&=&\pi r\cdot {\frac {\alpha }{180}}\end{matrix}}}
A
=
π
(
r
2
2
−
r
1
2
)
U
=
2
π
(
r
1
+
r
2
)
{\displaystyle {\begin{matrix}A&=&\pi \left(r_{2}^{2}-r_{1}^{2}\right)\\U&=&2\pi \left(r_{1}+r_{2}\right)\end{matrix}}}
V
=
π
r
2
h
3
O
=
π
r
2
+
π
⋅
r
⋅
s
M
=
π
⋅
r
⋅
s
{\displaystyle {\begin{matrix}V&=&{\frac {\pi r^{2}h}{3}}\\O&=&\pi r^{2}+\pi \cdot r\cdot s\\M&=&\pi \cdot r\cdot s&\end{matrix}}}
V
=
π
h
3
⋅
(
r
1
2
+
r
1
r
2
+
r
2
2
)
O
=
π
(
r
1
2
+
r
2
2
)
+
π
s
⋅
(
r
1
+
r
2
)
M
=
π
s
⋅
(
r
1
+
r
2
)
{\displaystyle {\begin{matrix}V&=&{\frac {\pi h}{3}}\cdot \left(r_{1}^{2}+r_{1}r_{2}+r_{2}^{2}\right)\\O&=&\pi \left(r_{1}^{2}+r_{2}^{2}\right)+\pi s\cdot \left(r_{1}+r_{2}\right)\\M&=&\pi s\cdot \left(r_{1}+r_{2}\right)\end{matrix}}}
V
=
4
3
π
r
3
O
=
4
π
r
2
{\displaystyle {\begin{matrix}V&=&{\frac {4}{3}}\pi r^{3}\\O&=&4\pi r^{2}\\\end{matrix}}}
V
=
π
r
2
h
O
=
2
G
+
M
=
2
π
r
(
h
+
r
)
M
=
2
π
r
⋅
h
=
π
d
⋅
h
{\displaystyle {\begin{matrix}V&=&\pi r^{2}h\\O&=&2G+M=2\pi r\left(h+r\right)\\M&=&2\pi r\cdot h=\pi d\cdot h\end{matrix}}}
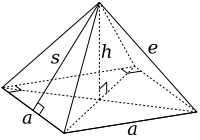
V
=
1
3
a
2
h
O
=
2
a
s
+
a
2
M
=
4
⋅
a
s
2
=
2
a
s
{\displaystyle {\begin{matrix}V&=&{\frac {1}{3}}a^{2}h\\O&=&2as+a^{2}\\M&=&4\cdot {\frac {as}{2}}=2as\end{matrix}}}
V
=
1
3
h
(
a
1
2
+
a
1
a
2
+
a
2
2
)
O
=
a
1
2
+
a
2
2
+
2
s
(
a
1
+
a
2
)
M
=
2
s
(
a
1
+
a
2
)
{\displaystyle {\begin{matrix}V&=&{\frac {1}{3}}h\left(a_{1}^{2}+a_{1}a_{2}+a_{2}^{2}\right)\\O&=&a_{1}^{2}+a_{2}^{2}+2s\left(a_{1}+a_{2}\right)\\M&=&2s\left(a_{1}+a_{2}\right)\end{matrix}}}
Ein Vieleck mit n Ecken nennt man auch n-Eck. Der Umfang eines n-Ecks berechnet sich durch:
U
=
a
+
b
+
c
+
.
.
.
+
(
n
−
1
)
+
n
{\displaystyle U=a+b+c+...+(n-1)+n}
Der Flächeninhalt eines n-Ecks wird durch Flächenzerlegung berechnet. Beispiel am regelmäßigen 6-Eck.
Wir betrachten, das Dreieck das aus dem Mittelpunkt des Sechsecks sowie zwei benachbarten Eckpunkten gebildet wird.
Aus der Innenwinkelsumme sowie der Symmertrie der Figur ergibt sich, dass die beiden Innenwinkel des Dreiecks an den Eckpunkten des Sechsecks je
60
∘
{\displaystyle 60^{\circ }}
h
{\displaystyle h}
a
2
{\displaystyle {\frac {a}{2}}}
a
{\displaystyle a}
h
{\displaystyle h}
h
=
a
2
−
(
a
2
)
2
=
3
4
a
2
=
1
2
3
⋅
a
{\displaystyle h={\sqrt {a^{2}-\left({\frac {a}{2}}\right)^{2}}}={\sqrt {{\frac {3}{4}}a^{2}}}={\frac {1}{2}}{\sqrt {3}}\cdot a}
Nun berechnen wir die Fläche des gleichseitigen Dreiecks durch Grundseite mal Höhe durch Zwei:
1
2
g
h
=
1
2
a
⋅
1
2
3
⋅
a
=
1
4
3
a
2
{\displaystyle {\frac {1}{2}}gh={\frac {1}{2}}a\cdot {\frac {1}{2}}{\sqrt {3}}\cdot a={\frac {1}{4}}{\sqrt {3}}a^{2}}
Da das Sechseck in insgesamt sechs derartige Flächen zerlegt werden kann, ergibt sich die Fläche des Sechsecks zu:
A
=
6
⋅
1
4
3
a
2
=
3
2
3
a
2
{\displaystyle A=6\cdot {\frac {1}{4}}{\sqrt {3}}a^{2}={\frac {3}{2}}{\sqrt {3}}a^{2}}
P
r
o
z
e
n
t
s
a
t
z
=
p
%
{\displaystyle \mathrm {Prozentsatz} =p\%}
G
r
u
n
d
w
e
r
t
=
G
{\displaystyle \mathrm {Grundwert} =G}
P
r
o
z
e
n
t
w
e
r
t
=
W
{\displaystyle \mathrm {Prozentwert} =W}
W
=
G
⋅
p
%
=
G
⋅
p
100
⇔
G
=
W
⋅
100
p
⇔
p
=
W
⋅
100
G
{\displaystyle {\begin{matrix}&W&=&G\cdot p\%=G\cdot {\frac {p}{100}}\\\Leftrightarrow &G&=&{\frac {W\cdot 100}{p}}\Leftrightarrow &p&=&{\frac {W\cdot 100}{G}}\end{matrix}}}
Z
i
n
s
s
a
t
z
=
p
%
{\displaystyle \mathrm {Zinssatz} =p\%}
Z
i
n
s
s
a
t
z
=
z
%
{\displaystyle \mathrm {Zinssatz} =z\%}
K
a
p
i
t
a
l
=
K
{\displaystyle \mathrm {Kapital} =K}
Z
i
n
s
w
e
r
t
=
Z
{\displaystyle \mathrm {Zinswert} =Z}
Z
=
K
⋅
p
%
=
K
⋅
p
100
⇔
K
=
Z
⋅
100
p
⇔
p
=
Z
⋅
100
K
{\displaystyle {\begin{matrix}&Z&=&K\cdot p\%=K\cdot {\frac {p}{100}}\\\Leftrightarrow &K&=&{\frac {Z\cdot 100}{p}}\Leftrightarrow &p&=&{\frac {Z\cdot 100}{K}}\end{matrix}}}
T
a
g
e
=
t
{\displaystyle \mathrm {Tage} =t}
M
o
n
a
t
e
=
m
{\displaystyle \mathrm {Monate} =m}
Z
=
K
⋅
p
%
⋅
t
360
=
K
⋅
p
%
⋅
m
12
⇔
K
=
Z
⋅
36000
p
⋅
t
=
Z
⋅
1200
p
⋅
m
⇔
p
=
Z
⋅
36000
K
⋅
t
=
Z
⋅
1200
K
⋅
m
{\displaystyle {\begin{matrix}&Z&=&K\cdot p\%\cdot {\frac {t}{360}}=K\cdot p\%\cdot {\frac {m}{12}}\\\Leftrightarrow &K&=&{\frac {Z\cdot 36000}{p\cdot t}}={\frac {Z\cdot 1200}{p\cdot m}}\Leftrightarrow &p&=&{\frac {Z\cdot 36000}{K\cdot t}}={\frac {Z\cdot 1200}{K\cdot m}}\end{matrix}}}
neues Kapital
=
K
n
{\displaystyle {\text{neues Kapital}}=K_{n}}
A
n
f
a
n
g
s
k
a
p
i
t
a
l
=
K
0
{\displaystyle \mathrm {Anfangskapital} =K_{0}}
J
a
h
r
e
=
n
{\displaystyle \mathrm {Jahre} =n}
K
n
=
K
0
⋅
(
1
+
p
%
)
n
=
K
0
⋅
(
1
+
p
100
)
n
⇔
K
0
=
K
n
(
1
+
p
%
)
n
=
K
n
(
1
+
p
100
)
n
⇔
p
=
(
K
n
K
0
n
−
1
)
⋅
100
{\displaystyle {\begin{matrix}&K_{n}&=&K_{0}\cdot \left(1+p\%\right)^{n}=K_{0}\cdot \left(1+{\frac {p}{100}}\right)^{n}\\\Leftrightarrow &K_{0}&=&{\frac {K_{n}}{\left(1+p\%\right)^{n}}}={\frac {K_{n}}{\left(1+{\frac {p}{100}}\right)^{n}}}\\\Leftrightarrow &p&=&\left({\sqrt[{n}]{\frac {K_{n}}{K_{0}}}}-1\right)\cdot 100\end{matrix}}}
Allgemeine Funktionsgleichung:
g
(
x
)
=
m
⋅
x
+
b
y
=
m
⋅
x
+
b
{\displaystyle {\begin{matrix}g(x)&=&m\cdot x+b\\y&=&m\cdot x+b\end{matrix}}}
m
{\displaystyle m}
b
{\displaystyle b}
g
1
{\displaystyle g_{1}}
0
m
{\displaystyle 0\mathrm {m} }
5
m
s
{\displaystyle 5{\frac {\mathrm {m} }{\mathrm {s} }}}
g
2
{\displaystyle g_{2}}
20
m
{\displaystyle 20\mathrm {m} }
7
m
s
{\displaystyle 7{\frac {\mathrm {m} }{\mathrm {s} }}}
g
1
(
x
)
=
5
x
g
2
(
x
)
=
−
7
x
+
20
{\displaystyle {\begin{matrix}g_{1}(x)&=&5x\\g_{2}(x)&=&-7x+20\end{matrix}}}
5
x
=
−
7
x
+
20
|
+
7
x
12
x
=
20
|
:
12
x
=
20
12
=
5
3
=
1
,
6
¯
s
g
(
x
)
=
25
3
=
8
,
3
¯
m
{\displaystyle {\begin{matrix}5x&=&-7x+20&|&+7x\\12x&=&20&|&:12\\x&=&{\frac {20}{12}}={\frac {5}{3}}=1{,}{\overline {6}}\mathrm {s} &&\\g(x)&=&{\frac {25}{3}}=8{,}{\overline {3}}\mathrm {m} &&\end{matrix}}}
Zur Bestimmung des Schnittpunkte linearer Gleichungen. Sie können auch mit anderen Funktionen mit mehreren Variablen verwendet werden.
I
y
=
10
x
+
1
I
I
y
=
−
5
x
+
10
|
⋅
2
}
+
I
y
=
10
x
+
1
I
I
⋅
2
2
y
=
−
10
x
+
20
I
I
I
3
y
=
0
x
+
21
⇔
3
y
=
21
|
:
3
⇔
y
=
7
{\displaystyle {\begin{array}{c}\left.{\begin{matrix}\mathrm {I} &y&=&10x+1&\\\mathrm {II} &y&=&-5x+10&|\cdot 2\end{matrix}}\right\rbrace +\\\hline {\begin{matrix}\mathrm {I} &y&=&10x+1&\\\mathrm {II\cdot 2} {\text{ }}&2y&=&-10x+20&\end{matrix}}\\\hline {\begin{matrix}\mathrm {III} &&3y&=&0x+21&\\&\Leftrightarrow &3y&=&21&|:3\\&\Leftrightarrow &y&=&7&\end{matrix}}\\\end{array}}}
einsetzen:
y
=
7
⇒
10
x
+
1
=
7
|
−
1
⇔
10
x
=
6
|
:
10
⇔
x
=
0
,
1
{\displaystyle {\begin{matrix}y=7&\Rightarrow &10x+1&=&7&|-1\\&\Leftrightarrow &10x&=&6&|:10\\&\Leftrightarrow &x&=&0,1&\end{matrix}}}
I
y
=
10
x
+
1
I
I
x
=
−
1
5
y
+
2
|
⋅
2
{\displaystyle {\begin{matrix}\mathrm {I} &y&=&10x+1&\\\mathrm {II} &x&=&-{\frac {1}{5}}y+2&|\cdot 2\end{matrix}}}
I
I
{\displaystyle \mathrm {II} }
I
{\displaystyle \mathrm {I} }
y
=
10
⋅
(
−
1
5
y
+
2
)
+
1
{\displaystyle y=10\cdot \left(-{\frac {1}{5}}y+2\right)+1}
ausmultiplizieren
y
=
−
2
y
+
20
+
1
|
+
2
y
⇔
3
y
=
21
|
:
3
⇔
y
=
7
{\displaystyle {\begin{matrix}&y&=&-2y+20+1&|&+2y\\\Leftrightarrow &3y&=&21&|&:3\\\Leftrightarrow &y&=&7&&\end{matrix}}}
einsetzen:
y
=
7
⇒
x
=
−
1
5
⋅
7
+
2
=
−
7
5
+
10
5
=
3
5
=
0
,
6
{\displaystyle y=7\Rightarrow x=-{\frac {1}{5}}\cdot 7+2=-{\frac {7}{5}}+{\frac {10}{5}}={\frac {3}{5}}=0,6}
I
y
=
10
x
+
1
I
I
y
=
−
5
x
+
10
{\displaystyle {\begin{matrix}\mathrm {I} &y&=&10x+1&\\\mathrm {II} &y&=&-5x+10&\end{matrix}}}
Gleichsetzen
y
=
y
{\displaystyle y=y}
10
x
+
1
=
−
5
x
+
10
|
+
5
x
⇔
15
x
+
1
=
10
|
−
1
⇔
15
x
=
9
|
:
15
⇔
x
=
0
,
6
{\displaystyle {\begin{matrix}&10x+1&=&-5x+10&|&+5x\\\Leftrightarrow &15x+1&=&10&|&-1\\\Leftrightarrow &15x&=&9&|&:15\\\Leftrightarrow &x&=&0,6\end{matrix}}}
einsetzen:
x
=
0.6
⇒
y
=
10
⋅
0
,
6
+
1
=
6
+
1
=
7
{\displaystyle x=0.6\Rightarrow y=10\cdot 0,6+1=6+1=7}
Bei mehreren Variablen braucht man soviele Gleichungen wie Variablen
I
2
x
+
3
y
+
4
z
=
11
I
I
3
x
+
4
y
+
z
=
11
I
I
I
4
x
+
2
y
+
3
z
=
13
I
2
x
+
3
y
+
4
x
=
11
⇔
I
3
⋅
I
−
2
⋅
I
I
y
+
10
z
=
11
⇔
I
V
−
2
⋅
I
+
I
I
−
4
y
−
5
z
=
−
9
⇔
V
I
2
x
+
3
y
+
4
z
=
11
I
V
y
+
10
z
=
11
4
⋅
I
V
+
V
35
z
=
35
⇔
z
=
1
{\displaystyle {\begin{array}{c}{\begin{matrix}\mathrm {I} &2x+3y+4z&=&11\\\mathrm {II} &3x+4y+z&=&11\\\mathrm {III} &4x+2y+3z&=&13\\\end{matrix}}\\\hline {\begin{matrix}\mathrm {I} &2x+3y+4x&=&11&\Leftrightarrow \mathrm {I} \\3\cdot \mathrm {I} -2\cdot \mathrm {II} &y+10z&=&11&\Leftrightarrow \mathrm {IV} \\-2\cdot \mathrm {I} +\mathrm {II} &-4y-5z&=&-9&\Leftrightarrow \mathrm {V} \\\end{matrix}}\\\hline {\begin{matrix}\mathrm {I} &2x+3y+4z&=&11\\\mathrm {IV} &y+10z&=&11\\4\cdot \mathrm {IV} +\mathrm {V} &35z&=&35&\Leftrightarrow z=1\end{matrix}}\end{array}}}
einsetzen in
I
V
{\displaystyle IV}
y
+
10
=
11
|
−
10
⇔
y
=
1
{\displaystyle {\begin{matrix}&y+10&=&11&|-10\\\Leftrightarrow &y&=&1\end{matrix}}}
einsetzen in
I
{\displaystyle I}
2
x
+
3
+
4
=
11
|
−
7
⇔
2
x
=
4
|
:
2
⇔
x
=
2
{\displaystyle {\begin{matrix}&2x+3+4&=&11&|&-7\\\Leftrightarrow &2x&=&4&|&:2\\\Leftrightarrow &x&=&2\\\end{matrix}}}
Probe (in
I
I
{\displaystyle \mathrm {II} }
I
I
I
{\displaystyle \mathrm {III} }
I
I
3
⋅
2
+
4
⋅
1
+
1
⋅
1
=
11
6
+
4
+
1
=
11
11
=
11
{\displaystyle {\begin{matrix}\mathrm {II} &3\cdot 2+4\cdot 1+1\cdot 1&=&11\\&6+4+1&=&11\\&11&=&11\\\end{matrix}}}
allgemeine Form:
f
(
x
)
=
a
x
2
+
b
x
+
c
{\displaystyle f(x)=ax^{2}+bx+c}
Scheitelpunktform:
a
(
x
+
d
)
2
+
e
{\displaystyle a\left(x+d\right)^{2}+e}
S
(
−
d
|
e
)
{\displaystyle S\left(-d|e\right)}
der „a“ Faktor
a
<
0
{\displaystyle a<0}
die Parabel ist nach unten geöffnet
a
>
0
{\displaystyle a>0}
die Parabel ist nach oben geöffnet
|
a
|
=
1
{\displaystyle |a|=1}
Normalparabel
|
a
|
>
1
{\displaystyle |a|>1}
gestreckte (schmale) Parabel
|
a
|
<
1
{\displaystyle |a|<1}
gestauchte (breite) Parabel
Umwandlung aus der algemeinen Form in die Scheitelpunktform:
f
(
x
)
=
a
x
2
+
b
x
+
c
|
a ausklammern
f
(
x
)
=
a
(
x
2
+
b
a
x
+
c
a
)
|
quadratische
E
r
g
a
¨
n
z
u
n
g
f
(
x
)
=
a
(
x
2
+
b
a
x
+
(
b
2
a
)
2
−
(
b
2
a
)
2
⏟
quadratische
E
r
g
a
¨
n
z
u
n
g
+
c
a
)
{\displaystyle {\begin{matrix}f(x)&=&ax^{2}+bx+c&|&{\text{a ausklammern}}\\f(x)&=&a\left(x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}\right)&|&{\text{quadratische }}\mathrm {Erg{\ddot {a}}nzung} \\f(x)&=&a\left(x^{2}+{\frac {b}{a}}x+\underbrace {\left({\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}} _{{\text{quadratische }}\mathrm {Erg{\ddot {a}}nzung} }+{\frac {c}{a}}\right)&&\end{matrix}}}
Das nennt man quadratische Ergänzung, da man den „
b
{\displaystyle b}
Es gibt die erste Binomische Formel:
x
2
+
b
a
x
+
(
b
2
a
)
2
=
(
x
+
b
2
a
)
2
{\displaystyle x^{2}+{\frac {b}{a}}x+\left({\frac {b}{2a}}\right)^{2}=\left(x+{\frac {b}{2a}}\right)^{2}}
⇒
f
(
x
)
=
a
(
(
x
+
b
2
a
)
2
−
(
b
2
a
)
2
+
c
a
)
|
a
u
s
m
u
l
t
i
p
l
i
z
i
e
r
e
n
⇔
f
(
x
)
=
a
(
x
+
b
2
a
⏟
d
)
2
−
(
b
2
4
a
−
c
⏟
c
)
{\displaystyle {\begin{matrix}&\Rightarrow &f(x)&=&a\left(\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {c}{a}}\right)&|\mathrm {ausmultiplizieren} \\&\Leftrightarrow &f(x)&=&a\left(x+\underbrace {\frac {b}{2a}} _{d}\right)^{2}-\left(\underbrace {{\frac {b^{2}}{4a}}-c} _{c}\right)&\end{matrix}}}
Aus der Form
f
(
x
)
=
a
(
(
x
+
b
2
a
)
2
−
(
b
2
a
)
2
+
c
a
)
{\displaystyle f(x)=a\left(\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {c}{a}}\right)}
f
(
x
)
=
0
{\displaystyle f(x)=0}
0
=
a
(
(
x
+
b
2
a
)
2
−
(
b
2
a
)
2
+
c
a
)
|
:
a
⇔
0
=
(
x
+
b
2
a
)
2
−
(
b
2
a
)
2
+
c
a
|
−
c
a
+
(
b
2
a
)
2
⇔
(
b
2
a
)
2
−
c
a
=
(
x
+
b
2
a
)
2
|
⇔
±
(
b
2
a
)
2
−
c
a
=
x
+
b
2
a
|
−
b
2
a
⇔
x
1
,
2
=
−
b
2
a
±
(
b
2
a
)
2
−
c
a
{\displaystyle {\begin{matrix}&&0&=&a\left(\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {c}{a}}\right)&|&:a\\&\Leftrightarrow &0&=&\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {c}{a}}&|&-{\frac {c}{a}}+\left({\frac {b}{2a}}\right)^{2}\\&\Leftrightarrow &\left({\frac {b}{2a}}\right)^{2}-{\frac {c}{a}}&=&\left(x+{\frac {b}{2a}}\right)^{\overset {\text{ }}{2}}&|&{\sqrt {\text{ }}}\\&\Leftrightarrow &\pm {\sqrt {\left({\frac {b}{2a}}\right)^{2}-{\frac {c}{a}}}}&=&x+{\frac {b}{2a}}&|&-{\frac {b}{2a}}\\&\Leftrightarrow &x_{1,2}&=&-{\frac {b}{2a}}\pm {\sqrt {\left({\frac {b}{2a}}\right)^{2}-{\frac {c}{a}}}}&&\end{matrix}}}
Die Formel ist auch unter dem Namen
p
q
{\displaystyle pq}
b
a
=
p
∧
c
a
=
q
{\displaystyle {\frac {b}{a}}=p\wedge {\frac {c}{a}}=q}
⇒
x
1
,
2
=
−
p
2
±
(
(
p
2
)
2
−
q
)
{\displaystyle \Rightarrow x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {(\left({\frac {p}{2}}\right)^{2}-q)}}}
Einige Parabelbeispiele
Nullpunkt (die Punkte an denen die Parabel die
x
{\displaystyle x}
→
p
q
{\displaystyle \rightarrow pq}
Scheitelpunkte (die
x
{\displaystyle x}
y
{\displaystyle y}
→
{\displaystyle \rightarrow }
Schnittpunke zweier Parabeln.
→
{\displaystyle \rightarrow }
x
{\displaystyle x}
y
{\displaystyle y}
f
(
x
)
1
=
f
(
x
)
2
⇔
a
1
x
2
+
b
1
x
+
c
1
=
a
2
x
2
+
b
2
x
+
c
3
{\displaystyle {\begin{matrix}&&f(x)_{1}=f(x)_{2}\\&\Leftrightarrow &a_{1}x^{2}+b_{1}x+c_{1}=a_{2}x^{2}+b_{2}x+c_{3}\end{matrix}}}
Natürliche Zahlen sind die Zahlen, die wie der Name schon sagt in der Natur vorkommen. Das heißt, sie sind „anfaßbar“.
z.B. 1 Apfel, 2 Personen, 10,- €
Die Menge der natürlichen Zahlen wird mit
N
{\displaystyle \mathbb {N} }
∈
N
{\displaystyle \in \mathbb {N} }
N
∗
{\displaystyle \mathbb {N} ^{*}}
0
{\displaystyle 0}
N
0
{\displaystyle \mathbb {N} _{0}}
Bei großen Zahlen empfielt es sich ofmals die Addition schriftlich durchzuführen.
Dazu schreibt man die zu berechnenden Zahlen übereinander (beginnend von rechts), so dass die Einer über den Einern stehen und die Zehner über den Zehneren usw.
Diese rechnet man von recht beginnend, von oben nach unten zusammen. Unten notiert man nur die Einer der errechneten Zahl. Den Rest addiert man zur nächsten Zahl usw.
z.B.
1
3
9
4
8
6
+
9
8
3
+
4
2
1
0
+
2
+
8
7
9
6
4
=
2
1
3
2
2
2
6
2
4
1
5
{\displaystyle {\begin{array}{c|c|c|c|c|c|c}&1&3&9&4&8&6\\+&&&&9&8&3\\+&&&4&2&1&0\\+&&&&&&2\\+&&8&7&9&6&4\\\hline =&{\overset {1}{2}}&{\overset {2}{3}}&{\overset {2}{2}}&{\overset {2}{6}}&{\overset {1}{4}}&5\\\hline \hline \end{array}}}
Nebenrechnung:
6
+
3
+
2
+
4
=
15
(
5 ist der Einer
)
8
+
8
+
1
+
6
+
1
=
24
4
+
9
+
2
+
9
+
2
=
26
9
+
4
+
7
+
2
=
22
3
+
8
+
2
=
13
1
+
1
=
2
{\displaystyle {\begin{matrix}6+3+2+4&=&15&{\text{ }}({\text{5 ist der Einer}})\\8+8+1+6+1&=&24&\\4+9+2+9+2&=&26&\\9+4+7+2&=&22&\\3+8+2&=&13&\\1+1&=&2&\end{matrix}}}
Die Schriftlich Subtraktrion funktioniert ähnlich der Addition. Auch hier schreiben wir die zu subtrahierenden Zahlen untereinander. Dann addiren wir alle übereinander stehenden Ziffern um diese dann von der entsprechenden Ziffer des Minuenden zu subtrahieren. Falls diese Summe größer ist als die entsprechende Ziffer des Minuenden, so wird ihr ein Zehner hinzugefügt, dieser wird jedoch zugleich als einer von der Ziffer links daneben subtrahiert.
z.B.
9
8
7
6
5
4
3
2
1
−
9
4
3
8
0
0
−
2
1
7
6
8
−
9
1
−
1
1
1
2
5
2
1
1
0
9
8
6
6
8
8
1
5
2
{\displaystyle {\begin{array}{cc|c|c|c|c|c|c|c|c}&9&8&7&6&5&4&3&2&1\\\hline -&&&&9&4&3&8&0&0\\-&&&&&2&1&7&6&8\\-&&&&&&&&9&1\\-&&&{\underset {1}{\text{ }}}&{\underset {1}{\text{ }}}&{\underset {1}{\text{ }}}&{\underset {2}{\text{ }}}&{\underset {2}{5}}&{\underset {1}{1}}&0\\\hline &9&8&6&6&8&8&1&5&2\\\hline \hline \end{array}}}
Nebenrechnung:
0
+
8
+
1
+
0
=
9
1
−
9
=
geht nicht
daher
11
−
9
=
2
0
+
6
+
9
+
1
+
1
=
17
2
−
17
=
geht nicht
daher
12
−
17
=
geht nicht
daher
22
−
17
=
5
8
+
7
+
5
+
2
=
22
3
−
22
=
geht nicht
daher
13
−
22
=
geht nicht
daher
23
−
22
=
1
3
+
1
+
2
=
6
4
−
6
=
geht nicht
daher
14
−
6
=
8
4
+
2
+
1
=
7
5
−
7
=
geht nicht
daher
15
−
7
=
8
9
+
1
=
10
6
−
10
=
geht nicht
daher
16
−
10
=
6
1
=
1
7
−
1
=
6
{\displaystyle {\begin{matrix}&0+8+1+0&=&9\\&1-9&=&{\text{geht nicht}}\\{\text{daher}}&11-9&=&2\\&0+6+9+1+1=17\\&2-17&=&{\text{geht nicht}}\\{\text{daher}}&12-17&=&{\text{geht nicht}}\\{\text{daher}}&22-17&=&5\\&8+7+5+2=22\\&3-22&=&{\text{geht nicht}}\\{\text{daher}}&13-22&=&{\text{geht nicht}}\\{\text{daher}}&23-22&=&1\\&3+1+2=6\\&4-6&=&{\text{geht nicht}}\\{\text{daher}}&14-6&=&8\\&4+2+1=7\\&5-7&=&{\text{geht nicht}}\\{\text{daher}}&15-7&=&8\\&9+1=10\\&6-10&=&{\text{geht nicht}}\\{\text{daher}}&16-10&=&6\\&1&=&1\\&7-1&=&6\\\end{matrix}}}
Beispiel 2:
4
3
2
1
+
2
1
0
−
9
1
−
1
1
0
1
1
4
3
3
9
{\displaystyle {\begin{array}{cc|c|c|c}&4&3&2&1\\\hline +&&2&1&0\\-&&&9&1\\-&&{\underset {1}{1}}&{\underset {1}{0}}&1\\\hline &4&3&3&9\\\hline \hline \end{array}}}
Nebenrechnung:
1
+
0
=
1
⊕
1
+
1
=
2
⊖
1
−
2
=
geht nicht
11
−
2
=
9
2
+
1
=
3
⊕
9
+
0
+
1
=
10
⊖
3
−
10
=
geht nicht
13
−
10
=
3
11
−
2
=
9
3
+
2
=
5
⊕
1
+
1
=
2
⊖
5
−
2
=
3
4
−
0
=
4
{\displaystyle {\begin{matrix}1+0&=&1&\oplus \\1+1&=&2&\ominus \\1-2&=&{\text{geht nicht}}\\11-2&=&9\\2+1&=&3&\oplus \\9+0+1&=&10&\ominus \\3-10&=&{\text{geht nicht}}\\13-10&=&3\\11-2&=&9\\3+2&=&5&\oplus \\1+1&=&2&\ominus \\5-2&=&3\\4-0&=&4\end{matrix}}}
Auch die schriftliche Multiplikation funktioniert nach dem Prinzip der schriftlichen Addition. Bloß wir hier nicht addiert sonden multipliziert.
1
2
3
4
5
6
⋅
3
7
8
9
1
8
2
7
3
6
4
4
4
8
8
1
6
2
4
3
1
3
9
4
2
3
7
1
0
1
3
1
6
1
8
4
1
6
1
6
1
6
1
6
2
3
6
8
{\displaystyle {\begin{array}{c|c|c|c|c|c|c|c|c|c}1&2&3&4&5&6&\cdot &3&7&8\\\hline &&&&{\overset {1}{9}}&{\overset {2}{8}}&{\overset {3}{7}}&{\overset {4}{6}}&{\overset {4}{4}}&8\\&&&{\overset {1}{8}}&{\overset {2}{6}}&{\overset {3}{4}}&{\overset {3}{1}}&{\overset {4}{9}}&2&\\&&3&{\overset {1}{7}}&{\overset {1}{0}}&{\overset {1}{3}}&{\overset {1}{6}}&8&&\\\hline &&{\overset {1}{4}}&{\overset {1}{6}}&{\overset {1}{6}}&{\overset {1}{6}}&{\overset {2}{6}}&3&6&8\\\hline \hline \end{array}}}
Nebenrechung:
Man beginnt mit den beiden Ziffern ganz rechts. Also mit 6 und 8.
6
⋅
8
=
48
{\displaystyle 6\cdot 8=48}
Nun geht man in der ersten Zahl von der 6 Ziffer links von ihr. Also zur 5.
5
⋅
8
=
40
{\displaystyle 5\cdot 8=40}
Zu diesem Ergebniss addiert man die Ziffer die wir gerade an den oberen Rand des Kästchens geschrieben haben. Also 4.
40
+
4
=
44
{\displaystyle 40+4=44}
Die 4 auf der Einerstelle kommt nun in die mitte der Kästenchens links von der 8. Die 4 auf der Zehnerstelle kommt Links daneben an den oberen Rand des Kästchens. Danch wir dieses Verfahren immer weiter wiederholt.
8
⋅
4
=
32
32
+
4
=
3
¯
6
8
⋅
3
=
24
24
+
3
¯
=
2
_
7
8
⋅
2
=
16
16
+
2
_
=
18
8
⋅
1
=
8
8
+
1
=
9
{\displaystyle {\begin{matrix}8\cdot 4&=&32&&32+4&=&{\overline {3}}6\\8\cdot 3&=&24&&24+{\overline {3}}&=&{\underline {2}}7\\8\cdot 2&=&16&&16+{\underline {2}}&=&18\\8\cdot 1&=&8&&8+1&=&9\end{matrix}}}
Durch die Unter- bzw. Überstriche wurde angedeutet, dass die Ziffer 3 aus der ersten Zeile in der zweiten Zeile der Zahl 24 hinzuaddiert wird, bzw. die Ziffer 2 aus der zweiten Zeile der 16 in der dritten Zeile der Ziffer 16 hinzuaddiert wird. Analoges gilt natürlich auch für die Ziffer 1 der Zahl 18 in der dritten Zeile.
In den folgenden Zeilen verfährt man analog. Schließlich addiert man, die Ergebnisse auf, wie im Abschnitt über schriftliche addition beschrieben.
Es kommt schon mal vor, dass wir mit Zahlen rechnen, die nicht mehr Elemente der Natürlichen Zahlen sind. Die passiert schnell wenn man Zahlen teilen muss. Hierzu teilen wir nacheinander (von links nach rechts) eine Zahl durch einen Divisor. Geht diese nicht mehr, so setzen wir ein Komma im Divisor und ziehen der zu teilenden Zahl eine 0 hinzu.
9
8
4
3
:
1
2
=
820
,
25
9
6
2
4
2
4
0
3
0
0
0
3
0
2
4
6
0
6
0
0
{\displaystyle {\begin{array}{c|c|c|c|c|c|ccc}9&8&4&3&:&1&2&=&820{,}25\\9&6&&&&&&&\\\hline &2&4&&&&&&\\&2&4&&&&&&\\\hline &&0&3&&&&&\\&&0&0&&&&&\\\hline &&0&3&0&&&&\\&&&2&4&&&&\\\hline &&&&6&0&&&\\&&&&6&0&&&\\\hline &&&&&0&&&\\\end{array}}}



















































































![{\displaystyle {\sqrt[{n}]{\text{ }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c40d1bc03a1118686c952fd6595c4f7ae3f0364)












































































































![{\displaystyle {\begin{matrix}&K_{n}&=&K_{0}\cdot \left(1+p\%\right)^{n}=K_{0}\cdot \left(1+{\frac {p}{100}}\right)^{n}\\\Leftrightarrow &K_{0}&=&{\frac {K_{n}}{\left(1+p\%\right)^{n}}}={\frac {K_{n}}{\left(1+{\frac {p}{100}}\right)^{n}}}\\\Leftrightarrow &p&=&\left({\sqrt[{n}]{\frac {K_{n}}{K_{0}}}}-1\right)\cdot 100\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d3efe8d778c219438d301d64d87e595454f88bd)


































































