Benutzer:GRD/Konstruktion Bodediagramm mittels Asymptoten

Das Bodediagramm ist ein Hilfsmittel um Systemverhalten graphisch darzustellen. In diesem Abschnitt wird die Konstruktion aus einer Übertragungsfunktion zu einem Bode-Diagramm gezeigt. Das hier gezeigte Vorgehen ist nur eins von vielen Möglichkeiten ein Bode-Diagramm zu konstruieren. Es sollte beachtet werden, das dieser Artikel nicht das Verhalten von Totzeit-Gliedern berücksichtigt.

Darstellungsformen

Übertragungsfunktionen (in Zähler oder Nenner) können in verschiedenen Formen dargestellt werden.

• Allgemeine Form $G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{3}s^{3}+b_{2}s^{2}+b_{1}s+b_{0}}{a_{3}s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}}={\frac {b_{3}s^{3}+b_{2}s^{2}+b_{1}s^{1}+b_{0}s^{0}}{a_{3}s^{3}+a_{2}s^{2}+a_{1}s^{1}+a_{0}s^{0}}}={\frac {Polynom_{1}}{Polynom_{2}}}={\frac {Glied_{1}}{Glied_{2}}}$
  In solch einer Form werden jeweils Zähler und Nenner auch als Polynome bezeichnet. Mehrere Polynome können multipliziert werden, die einzelnen Polynome werden dann auch als Glieder bezeichnet. Üblicherweise haben Übertragungsfunktion in der Allgemeinen Form eine unendliche Ordnung. Hier ist sie 3. Ordnung.
  

Beispiel: mehrere Polynome oder Glieder hintereinander

$G(s)=K{\frac {(c_{2}s^{2}+c_{1}s+c_{0})\cdot (d_{1}s+d_{0})}{(a_{1}s+a_{0})\cdot (b_{2}s^{2}+b_{1}s+b_{0})\cdot (s)}}=K{\frac {Polynom_{1}\cdot Polynom_{2}}{Polynom_{3}\cdot Polynom_{4}\cdot Polynom_{5}}}=K{\frac {Glied_{1}\cdot Glied_{2}}{Glied_{3}\cdot Glied_{4}\cdot Glied_{5}}}$

K ist eine Konstante. Irritierenderweise wird häufig sowas gemacht: K+x=K, da die Konstante vor dem Bruch immer K lautet. Man sieht also K in der Regel nicht an, welche Operationen mit ihr durchgeführt wurden.

• Zeitkonstantenform $Ts+1$ (Polynom 1. Ordnung), $T^{2}s^{2}+2DTs+1$ (Polynom 2. Ordnung). Dämpfung D, Zeitkonstante T. Summand mit der kleinsten Ordnung $s^{0}$ muss normiert sein (Eins betragen). Diese Form ist die Ausgangsform für das Bode-Diagramm. Mehrere Polynome können multipliziert werden, die einzelnen Polynome werden dann auch als Glieder bezeichnet.
  

Beispiel: Polynome/Glieder/Zeitkonstantenform

$G(s)=K{\frac {(PD1-Glied)\cdot (PD1-Glied)\cdot (PD2-Glied)\cdot (D-Glied)}{(PT1-Glied)\cdot (PT2-Glied)\cdot (PT1-Glied)}}=K{\frac {(T_{1}s+1)\cdot (T_{2}+1)\cdot (T_{2}^{2}s^{2}+2DT_{2}s+1)\cdot (s)}{(T_{3}s+1)\cdot (T_{4}^{2}s^{2}+2DTs+1)\cdot (T_{5}s+1)}}$

Im weiteren Verlauf wird auf die einzelnen Glieder näher eingegangen.

• Nullstellenform $(s-s_{n1})$ (Polynom 1. Ordnung), $(s-s_{n1})(s-s_{n2})$ (Polynom 2. Ordnung). Die Nullstellen $s_{n1}$, $s_{n2}$ eines Polynoms lassen sich als Linearfaktoren darstellen.
  

weitere Nullstellenform 2. Ordnung

$(T_{a}s+1)(T_{b}s+1)=(T_{a}T_{b})s^{2}+(T_{a}+T_{b})s+1$

• Polynomdarstellung $T_{2}^{2}s^{2}+T_{1}s+1$. Die Parameter $T_{2}$ und $T_{1}$ sind zwei verschiedene Parameter. Summand mit der kleinsten Ordnung $s^{0}$ muss normiert sein (Eins betragen).
  
  

Zusammengefasst:
$a_{2}s^{2}+a_{1}s+a_{0}=T^{2}s^{2}+2DTs+1=(T_{a}s+1)(T_{b}s+1)=(T_{a}T_{b})s^{2}+(T_{a}+T_{b})s+1=T_{2}^{2}s^{2}+T_{1}s+1=s^{2}+ps+q$

Die Schritte werden durch ausklappbare Beispiele begleitet. "Kompliziertes Beispiel Allgemein und mit Zahlenwerten" ist ein über die verschiedenen Schritte zusammenhängendes Beispiel.

Konstruktion

Schritt 1: Polynomdarstellung

Die vorliegende Übertragungsfunktion muss in einzelne Polynome/Glieder der Allgemeinen Form umgewandelt werden. Polynome höherer Ordnung lassen sich in Polynome niedriger Ordnung umrechnen (z.B. Abspaltung, Polynomdivision). Auf diese Weise entstehen nur Polynome mit der höchsten Ordnung 2. Falls im Zähler und Nenner gleichartige Polynome vorhanden sind, so können diese gekürzt werden.

Eine Normierung wird in einem der nachfolgenden Schritten durchgeführt, kann aber an dieser Stelle schon geschehen.

Beispiel: Abspaltung

$=s^{3}+s^{3}+s^{2}+3s$ (Ausgangsfunktion)

$=2s^{3}+s^{2}+3s$ (zusammengefasst)

$=(2s^{2}+s+3)s$ (s abgespaltet und Ergebnis)

Kompliziertes Beispiel Allgemein und mit Zahlenwerten

$G(s)={\frac {b_{1}s+b_{0}}{a_{2}s^{3}+a_{1}s^{2}+a_{0}s}}={\frac {5s+4}{3s^{3}+2s^{2}+6s}}$ (Ausgangsfunktion)

$G(s)={\frac {b_{1}s+b_{0}}{(a_{2}s^{2}+a_{1}s+a_{0})s}}={\frac {5s+4}{(3s^{2}+2s+6)s}}$ (Abspaltung)

Schritt 2: Bestimmung der Dämpfung für Polynome 2. Ordnung

Wenn man Polynome 2. Ordnung hat, so müssen diese auf komplexe Nullstellen überprüft werden. Dazu bestimmt man die Dämpfung. Ob im Zähler oder Nenner:

$c_{2}s^{2}+c_{1}s+c_{0}$ oder ${\frac {1}{c_{2}s^{2}+c_{1}s+c_{0}}}$

die Dämpfung lautet $D={\frac {c_{1}}{2{\sqrt {c_{0}c_{2}}}}}$

Die Koeffizienten sind anstatt a und b, mit c bezeichnet um zu verdeutlichen, das dessen Form für die Bestimmung von D unerheblich ist. Ist kein Polynom 2. Ordnung im Zähler oder Nenner vorhanden, dann kann auf diesen und den nächsten Schritt verzichtet werden.

Kompliziertes Beispiel Allgemein und mit Zahlenwerten

Im Nenner Polynom 2. Ordnung mit $a_{0}=6,a_{1}=2,a_{2}=3,D={\frac {a_{1}}{2{\sqrt {a_{0}a_{2}}}}}={\frac {2}{2{\sqrt {6\cdot 3}}}}=0,236$

Schritt 3: Nullstellen bestimmen für Polynome 2. Ordnung

Für den Fall das die Dämpfung

$D<1$

$D\geq 1$

Nix machen! Kompliziertes Beispiel Allgemein und mit Zahlenwerten Da die Dämpfung D=0,236 < 1 ist, kann das Polynom 2. Ordnung nicht in zwei Polynome 1. Ordnung zerlegt werden.

Für den Fall, das ein Polynom 2. Ordnung (ob Nenner oder Zähler) eine Dämpfung $D\geq 1$ besitzt, so muss das Polynom 2. Ordnung in zwei Glieder 1. Ordnung aufgeteilt werden. $c_{2}s^{2}+c_{1}s+c_{0}$, Nullstellen mit pq-Formel $p={\frac {c_{1}}{c_{2}}}$ und $q={\frac {c_{0}}{c_{2}}}$ Ergebnis sind allgemein die Nullstellen $s_{0}$ und $s_{1}$. Mithilfe von Linearfaktoren geht das Polynom über: $c_{2}s^{2}+c_{1}s+c_{0}\to (s-s_{0})(s-s_{1})$ Beispiel ${\frac {5s+4}{(27s^{2}+36s+3)s}}$ Polynom 2. Ordnung im Nenner, pq-Formel mit $p={\frac {4}{3}},q={\frac {1}{9}}$ Nullstellen: $s_{0}=-0,089s_{1}=-1,24$ ${\frac {5s+4}{(27s^{2}+36s+3)s}}\to {\frac {5s+4}{(s+0,089)(s+1,24)s}}$

Schritt 4: In Zeitkonstantenform überführen

Die Übertragungsfunktion muss in die Zeitkonstantenform überführt werden. Zeitkonstanten sind entscheidene Stellen im Bodediagramm, anhand dessen das Bodediagramm konstruiert wird. Für jedes Polynom muss ihre Zeitkonstante $T$ bestimmt werden. Entscheidend ist das alle Polynome in den Koeffizienten mit den kleinsten Potenzen mit Eins normiert sind.

Kompliziertes Beispiel Allgemein und mit Zahlenwerten

$={\frac {b_{1}s+b_{0}}{(a_{2}s^{2}+a_{1}s+a_{0})s}}={\frac {5s+4}{(3s^{2}+2s+6)s}}$

$={\frac {({\frac {1}{b_{0}}})}{({\frac {1}{b_{0}}})}}{\frac {(b_{1}s+b_{0})}{...}}={\frac {({\frac {1}{4}})}{({\frac {1}{4}})}}{\frac {(5s+4)}{...}}$ (erst Zähler normieren)

$={\frac {1}{({\frac {1}{b_{0}}})}}{\frac {({\frac {b_{1}}{b_{0}}}s+{\frac {b_{0}}{b_{0}}})}{...}}={\frac {1}{({\frac {1}{4}})}}{\frac {({\frac {5}{4}}s+{\frac {4}{4}})}{...}}$

$=b_{0}{\frac {({\frac {b_{1}}{b_{0}}}s+1)}{...}}=4{\frac {({\frac {5}{4}}s+1)}{...}}$

$=K_{1}{\frac {(T_{b}s+1)}{...}}=4{\frac {(1,2s+1)}{...}}$ (Zähler in Zeitkonstantenform normiert)

$=K_{1}{\frac {(T_{b}s+1)}{(a_{2}s^{2}+a_{1}s+a_{0})s}}=4{\frac {(1,2s+1)}{(3s^{2}+2s+6)s}}$ (jetzt Nenner normieren)

$=K_{1}{\frac {({\frac {1}{a_{0}}})}{({\frac {1}{a_{0}}})}}{\frac {(T_{b}s+1)}{(a_{2}s^{2}+a_{1}s+a_{0})s}}=4{\frac {({\frac {1}{6}})}{({\frac {1}{6}})}}{\frac {(1,2s+1)}{(3s^{2}+2s+6)s}}$

$=K_{1}{\frac {({\frac {1}{a_{0}}})}{1}}{\frac {(T_{b}s+1)}{({\frac {a_{2}}{a_{0}}}s^{2}+{\frac {a_{1}}{a_{0}}}s+{\frac {a_{0}}{a_{0}}})s}}=4{\frac {({\frac {1}{6}})}{1}}{\frac {(1,2s+1)}{({\frac {3}{6}}s^{2}+{\frac {2}{6}}s+{\frac {6}{6}})s}}$

$=({\frac {K_{1}}{a_{0}}}){\frac {(T_{b}s+1)}{({\frac {a_{2}}{a_{0}}}s^{2}+{\frac {a_{1}}{a_{0}}}s+1)s}}=({\frac {4}{6}}){\frac {(1,2s+1)}{({\frac {3}{6}}s^{2}+{\frac {2}{6}}s+1)s}}$

$=K{\frac {(T_{b}s+1)}{(T_{a}^{2}s^{2}+2DT_{a}s+1)s}}=({\frac {2}{3}}){\frac {(1,2s+1)}{({\frac {1}{2}}s^{2}+{\frac {1}{3}}s+1)s}}$ (Nenner in Zeitkonstantenform normiert)

Zum besseren Verständnis wurde zu Beginn K durch K₁ ersetzt. Normalerweise wird ausschliesslich K verwendet, irritierenderweise auch wenn K verändert wird.
In diesem Beispiel ist ein I-Glied (Polynom ${\frac {1}{s}}$) im Nenner. Dadurch wird K zu einer Zeitkonstante T. Dies würde auch mit einem D-Glied im Zähler geschehen:

$=({\frac {1}{T_{I}s}}){\frac {(T_{b}s+1)}{(T_{a}^{2}s^{2}+2DT_{a}s+1)}}=({\frac {2}{3}}{\frac {1}{s}}){\frac {(1,2s+1)}{({\frac {1}{2}}s^{2}+{\frac {1}{3}}s+1)}}$ (Zeitkonstantenform Ergebnis)

Wäre kein D- oder I-Glied vorhanden, dann würde K bestehen bleiben.

Schritt 5: Zeitkonstanten $T$ in Eckfrequenzen $\omega$ umwandeln

Eckfrequenzen $\omega$ sind die Stellen auf der Frequenz-Achse, an der "besondere" Ereignisse stattfinden. Für die spätere Verwendung wird für jedes Polynom bzw. Glied dessen Eckfrequenz $\omega$ bestimmt. Die Eckfrequenzen werden immer aus dem Kehrwert der Zeitkonstanten gebildet ( $\omega ={\frac {1}{T}}$ ). Diese finden sich in den Polynomen, als Koeffizienten der höchsten Potenzen. Insgesamt gibt es sieben verschiedene Glieder, welche alle in der Tabelle unten aufgelistet sind.

$K$	$Ts$	${\frac {1}{Ts}}$	$Ts+1$	${\frac {1}{Ts+1}}$	$T^{2}s^{2}+2DTs+1$	${\frac {1}{T^{2}s^{2}+2DTs+1}}$
$P-Glied$	$D-Glied$	$I-Glied$	$PD1-Glied$	$PT1-Glied$	$PD2-Glied$	$PT2-Glied$
Keine Eckfrequenz	1. Eckfrequenz $\omega _{1}={\frac {1}{T}}$		Eckfrequenz ohne Index $\omega ={\frac {1}{T}}$

Kompliziertes Beispiel Allgemein und mit Zahlenwerten

$=({\frac {1}{T_{I}s}}){\frac {(T_{b}s+1)}{(T_{a}^{2}s^{2}+2DT_{a}s+1)}}=({\frac {2}{3}}{\frac {1}{s}}){\frac {(1,2s+1)}{({\frac {1}{2}}s^{2}+{\frac {1}{3}}s+1)}}=({\frac {2}{3}}{\frac {1}{s}})\cdot (1,2s+1)\cdot {\frac {1}{({\frac {1}{2}}s^{2}+{\frac {1}{3}}s+1)}}=(I-Glied)\cdot (PD1-Glied)\cdot (PT2-Glied)$

$I-Glied:{\frac {1}{T_{I}s}}={\frac {2}{3}}{\frac {1}{s}}\to {\frac {1}{T_{I}}}=\omega _{1}={\frac {2}{3}}=0{,}{\overline {6}}$ (Erste Eckfrequenz)

$PD1-Glied:T_{b}s+1=(1,2s+1)\to T_{b}=1,2\to \omega ={\frac {1}{T_{b}}}={\frac {1}{1,2}}={\frac {1}{({\frac {6}{5}})}}={\frac {5}{6}}=0,83$ (Eckfrequenz ohne Index)

$PT2-Glied:{\frac {1}{(T_{a}^{2}s^{2}+2DT_{a}s+1)}}={\frac {1}{({\frac {1}{2}}s^{2}+{\frac {1}{3}}s+1)}}\to T_{a}^{2}={\frac {1}{2}}\to T_{a}=0,707\to \omega ={\frac {1}{T_{a}}}={\frac {1}{0,707}}=1,41$ (Eckfrequenz ohne Index)

Schritt 6: Eckfrequenzen sortieren

Falls Eckfrequenzen vorliegen, so sollten diese in aufsteigender Reihenfolge mit einem Index (z.B. ω₁, ω₂, ω₃ usw.) versehen werden. Dies erleichtert später das einzeichnen der Asymptoten. Das Vorgehen beim Indizieren wird folgendermassen empfohlen:

1. P-Glied: besitzt keine Eckfrequenz und muss nicht indiziert oder sortiert werden
   
   
2. D- oder I-Glied: ω₁
   Falls ein D- oder I-Glied vorhanden ist, so ist diese die erste einzuzeichnende Eckfrequenz ω₁, da diese eine hervorgehobene Stellung beim Einzeichnen der Asymptoten einnehmen.
   
   
3. PD1-, PT1-, PD2- oder PT2-Glied: (ω₁), ω₂, ω₃, ω₄...
   Falls weitere Eckfrequenzen (aus PD1-, PT1-, PD2- oder PT2-Gliedern) vorhanden sind, werden diese der Grösse nach sortiert und mit einem Index ab Zwei versehen. Wenn kein D- oder I-Glied vorhanden ist, dann muss natürlich mit dem Index Eins begonnen werden.
   
   

Kompliziertes Beispiel Allgemein und mit Zahlenwerten

$I-Glied:\omega _{1}=0{,}{\overline {6}}$ (D- oder I-Glieder sind immer erste Eckfrequenzen)

Den Rest nach aufsteigender Grösse indizieren:
$PD1-Glied:\omega _{2}=0,83$

$PT2-Glied:\omega _{3}=1,41$

Schritt 7: Eckfrequenzen einzeichnen

Es werden nun die sortierten Eckfrequenzen in ein Bode-Diagramm eingezeichnet. Beginnend bei Eins könnten sich bei drei Eckfrequenzen folgende Bilder ergeben:

Beispiel: Eingezeichnete Eckfrequenzen mit aufsteigenden Indices.

Zahlenwerte in der Amplitudenverstärkung und Phasenverschiebung haben in diesem Schritt noch keine Bedeutung und sind deshalb weggelassen.

Beispiel: Eingezeichnete Eckfrequenzen mit vertauschten Indices.

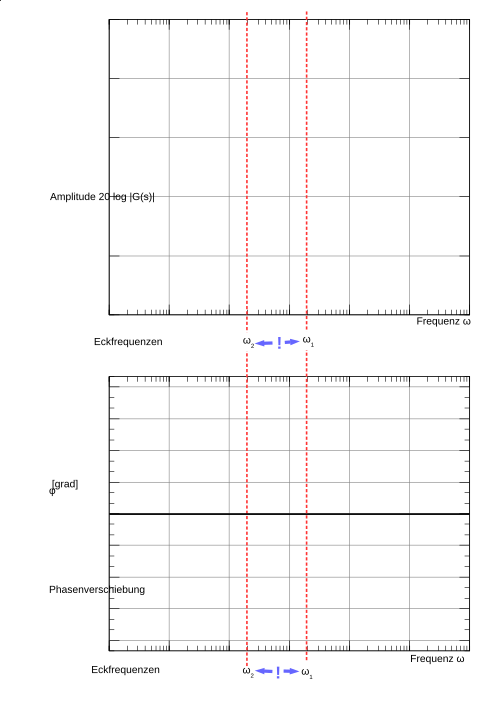
Es kann vorkommen, das ein D- oder I-Glied einen kleineren Index als Glieder mit höherer Ordnung besitzt, dazu ist weiter unten eine genauere Beschreibung vorhanden. Achsenbeschriftungen in der Amplitudenverstärkung und Phasenverschiebung haben in diesem Schritt noch keine Bedeutung und sind deshalb weggelassen.

Kompliziertes Beispiel Allgemein und mit Zahlenwerten

Es fällt auf, das die Eckfrequenzen sehr eng beieinander liegen. Des weiteren ist die Eckfrequenz vom I-Glied mit dem PD1- und PT2-Glied vertauscht. Das PD1-Glied befindet innerhalb des engen Zwischenraums von ω₂ und ω₁.

Schritt 8: Asymptoten einzeichnen

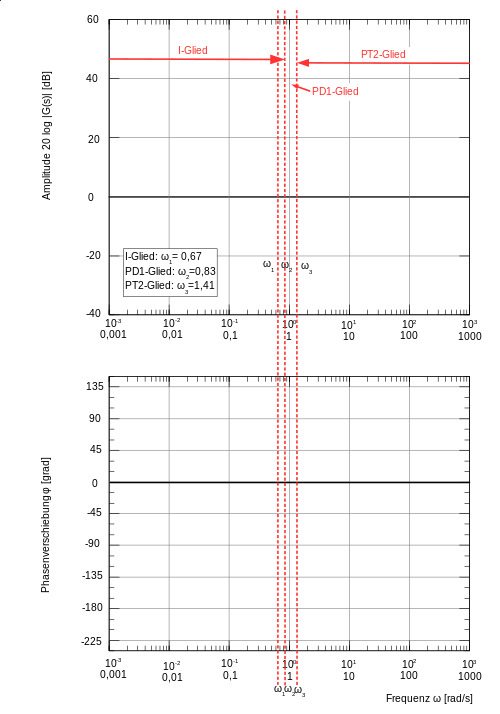
In der Tabelle sind alle vorhanden Glieder und dessen Asymptoten eingetragen die möglich sind- weitere sind nicht vorhanden! Das Entscheidene beim Einzeichnen der Asympoten ist Folgendes: Bei jeder Eckfrequenz findet an den Asymptoten eine relative Änderung der Steigung statt. Das bedeutet, das an den Eckfrequenz-Stellen eine Addition oder Subtraktion der Steigung stattfindet.

P-Glied	D-Glied	I-Glied	PD1-Glied	PT1-Glied	PD2-Glied	PT2-Glied
$K$	$Ts$	${\frac {1}{Ts}}$	$Ts+1$	${\frac {1}{Ts+1}}$	$T^{2}s^{2}+2DTs+1$	${\frac {1}{T^{2}s^{2}+2DTs+1}}$
Gerade mit Abstand 20 log |K| von der Achse. Asymptote mit Steigung null.	Schnittpunkt bei 0 dB und ω-Eckfrequenz. Asymptote mit Steigung plus 20 dB/Dekade links und rechts der Eckfrequenz.	Schnittpunkt bei 0 dB und ω-Eckfrequenz. Asymptote mit Steigung minus 20 dB/Dekade links und rechts der Eckfrequenz.	Asymptote mit zusätzlicher Steigung 20 dB/Dekade rechts der Eckfrequenz.	Asymptote mit abzüglicher Steigung 20 dB/Dekade rechts der Eckfrequenz.	Asymptote mit zusätzlicher Steigung 40 dB/Dekade rechts der Eckfrequenz.	Asymptote mit abzüglicher Steigung 40 dB/Dekade rechts der Eckfrequenz.
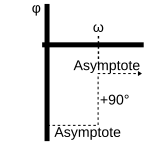
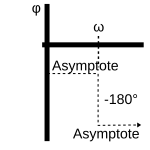
Keine Phasenverschiebung vorhanden. Asymptote direkt auf Achse.	Phasenverschiebung durchgängig bei +90°.	Phasenverschiebung durchgängig bei -90°.	An der Stelle der ω-Eckfrequenz findet eine Phasenverschiebung von +90° statt.	An der Stelle der ω-Eckfrequenz findet eine Phasenverschiebung von -90° statt.	An der Stelle der ω-Eckfrequenz findet eine Phasenverschiebung von +180° statt.	An der Stelle der ω-Eckfrequenz findet eine Phasenverschiebung von -180° statt.

Es werden nun die einzelnen Asymptoten eingetragen. Die Reihenfolge ist zu beachten:

Schritt 1a: Asymptote D- oder I-Glied einzeichnen

Sollte ein D- oder I-Glied vorhanden sein, so muss dieser jetzt eingezeichnet werden. Nach Tabelle hat die Asymptote der Amplitude eines D-/I-Gliedes eine Steigung von +/- 20 dB/Dekade. Die Asymptote muss durch den Schnittpunkt 0 dB und der eigenen Eckfrequenz ω₁ gehen. Die Asymptote endet an der darauf folgenden Eckfrequenz ω₂. Die Phasenverschiebung beträgt bis zur darauf folgenden Eckfrequenz +/- 90°. Ein K-Wert ist bei einem D- oder I-Glied nicht vorhanden und findet sich in der Zeitkonstante T und somit in der Eckfrequenz ω₁ wieder. Oder anders ausgedrückt: Wenn es ein D- oder I-Glied geben sollte, dann gibt es kein P-Glied.
Beispiel: Ein D-Glied. Es steigt mit 20 dB/Dekade und schneidet die Frequenz-Achse bei der Amplitude 0 und der Eckfrequenz. Die Phasenverschiebung beträgt +90°.

Schritt 1b: Asymptote P-Glied einzeichnen

Wenn ein P-Glied (K-Wert) vorhanden ist, dann wird als erstes dessen Asymptote bis zur ersten Eckfrequenz (eines anderen Gliedes) eingetragen. Sollte ein P-Glied vorhanden sein, dann ist kein D- oder I-Glied vorhanden. Wie in der Tabelle angegeben wird dessen Amplitudenwert mittels 20 log|K| berechnet, die Phasenverschiebung beträgt bei einem P-Glied 0°. Falls keine Eckfrequenz vorhanden sein sollte, so wird die Asymptote ins Unendliche geführt.
Falls eine Eckfrequenz vorhanden sein sollte, so könnte sich folgendes Bild ergeben:

Kompliziertes Beispiel Allgemein und mit Zahlenwerten

Wie angegeben muss zuerst das I-Glied eingetragen werden. Das hat eine Steigung von -20dB/Dekade. Es muss seine Eckfrequenz bei 0 dB schneiden. Die Asymptote selbst geht nur bis zur Eckfrequenz vom nächsten Glied, in diesem Fall PD1-Glied.

Schritt 2: Asymptoten der verbleibenden PD1-/PT1-/PD2- und PT2-Glieder werden genau dort fortgesetzt, wo die vorherigen Asymptoten enden.

Beispiel Asymptote P-Glied und PT1-Glied

Die Asymptote des P-Gliedes endet an der ω₁-Eckfrequenz des PT1-Gliedes. Im Falle der Amplitude fällt nach Tabelle ein PT1-Glied mit -20 dB/Dekade. Wenn die Steigung vorher 0 dB/Dekade war, so wird diese um 20 dB/Dekade verringert. Die Asymptote der Phasenverschiebung wird um -90° (nach unten) verschoben.

Beispiel Asymptote D-Glied und PT1-Glied

Die Steigung des D-Glieds beträgt +20 dB/Dekade. An der Eckfrequenz wird diese um 20 dB/Dekade verringert, übrig bleibt eine Steigung von 0 dB/Dekade (+20-20=0). Nochmal: Die Steigung beträgt nicht -20 dB/Dekade, sondern wird um 20 dB/Dekade verringert. Die Phasenverschiebung fällt um 90°.

Beispiel Asymptote P-Glied und PT2-Glied

Hier ist der gleiche Sachverhalt wie beim P- und PT1-Glied mit dem Unterschied, dass das PT2-Glied stärker fällt.

Beispiel Asymptote D-Glied und PT1-Glied mit vertauschten Indices

Man sollte sich nicht dadurch verunsichern lassen, wenn plötzlich ω₂ links von ω₁ liegen sollte. Das erklärt sich dadurch, wenn der Schnittpunkt, von einem D- oder I-Glied mit der Frequenzachse, weiter rechts liegt als eine nachfolgende Eckfrequenz. Man sollte dennoch mit ω₁ anfangen.

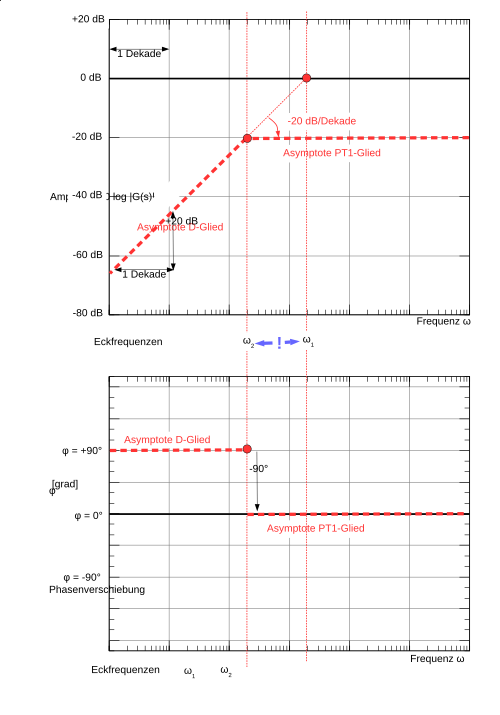
Kompliziertes Beispiel Allgemein und mit Zahlenwerten

Ab der Eckfrequenz vom PD1-Glied, steigt die Asymptote um zusätzliche 20dB/Dekade. Sie geht bis zur nächsten Eckfrequenz (hier PT2-Glied).

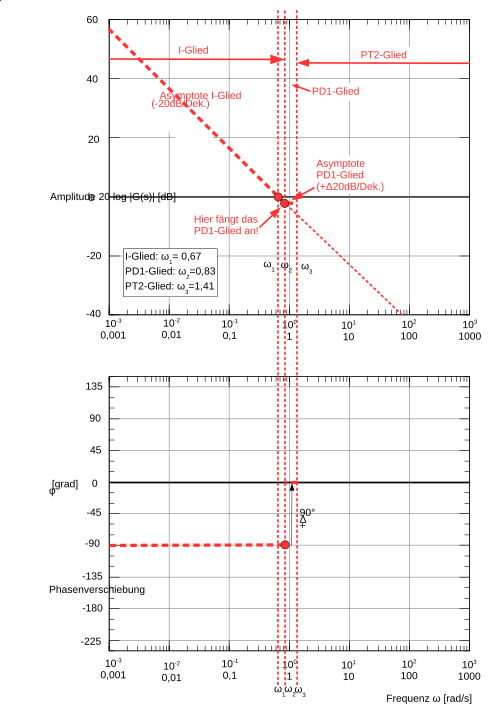
Ab der Eckfrequenz vom PT2-Glied, fällt die Asymptote um abzügliche 40dB/Dekade bis ins Unendliche.

Schritt 9: Abweichungen eintragen

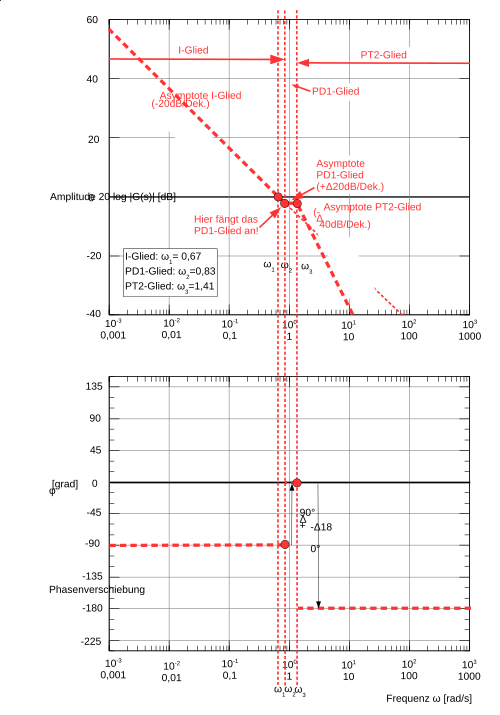
Beim Amplitudendiagramm sind an den Eckfrequenzen der Glieder 1. und 2. Ordnung Abweichungen zwischen der Asymptote und dem tatsächlichen graphischen Verlauf vorhanden.

3 dB Abweichung PD1- und PT1-Glieder

Bei PD1- und PT1-Gliedern beträgt an den Eckfrequenz-Stellen die Abweichung zwischen der Asymptote und dem tatsächlichen graphischen Verlauf immer 3 dB.
Bei einem PT1-Glied sieht das folgendermassen aus:

Die 3dB-Abweichung wird an alle PD1- und PT1-Eckfrequenzen eingetragen.

Resonanzüberhöhung PD2- und PT2-Glieder

PD2- oder PT2-Glieder mit kleinen Dämpfungen bekommen an ihren Eckfrequenzen eine Spitze nach unten (PD2) oder nach oben (PT1), sogenannte Resonanzüberhöhungen. Bei einem PT2-Glied sieht das folgendermassen aus:

Der Betrag dieser Spitze oder Resonanzüberhöhung lässt sich für 0 < D < 0,707 folgendermassen berechnen:
Resonanzüberhöhung $=20log({\frac {\sqrt {c_{0}c_{2}}}{c_{1}}})$ (für alle normierten Formen verwendbar)
oder

Resonanzüberhöhung $=20log(2D)$ (in Zeitkonstantenform mit vorhandener Dämpfung)

Kompliziertes Beispiel Allgemein und mit Zahlenwerten

Beim Übergang vom I- auf das PD1-Glied ist eine 3dB Abweichung vorhanden.
Die Resonanzüberhöhung am PT2-Glied beträgt:

$20log|2D|=20log|2\cdot 0,236|=6,52dB$
Mit entfernten Hilfslinien und eingezeichneten Abweichungen sieht das Bode-Diagramm folgendermassen aus:

Schritt 10: Graphischen Verlauf eintragen

Die Asymptoten sind nicht der graphische Verlauf, sondern nur die Asymptoten der einzelnen Übertragungsfunktionen. Zwischen den Eckfrequenzen wird die genaue Differenz nicht berücksichtigt und nur skizzenhaft gezeichnet. Der graphische Verlauf wird an den Asymptoten entlang, durch die 3 dB-Abweichungen und Resonanzüberhöhungen eingezeichnet.

Beispiel

Kompliziertes Beispiel Allgemein und mit Zahlenwerten