Benutzer:Lobsterbake

[aus "Blender Dokumentation: Boolean-Modifier". Bild und Teile des Textes wurden geändert. Die Überarbeitung ist in Arbeit. ]

[...]

Boolsche Operationen[Bearbeiten]

Difference

Zieht das zweite Objekt vom ersten ab. Hierbei sollten sie darauf achten in welcher Reihenfolge sie die Objekte selektieren, denn das aktive Objekt (das zuletzt ausgewählte) wird vom markierten Objekt (erste Objekt) abgezogen.

Union

Erzeugt ein neues Objekt, das das gesamte Volumen beider Objekte enthält. Wie sie in dem Bild sehen können wurde die Kugel dem Volumen des Würfels hinzugefügt.

Intersect

Erzeugt ein neues Objekt, das die Schnittmenge beider Volumina beinhaltet.

[...]

Kleine Einführung in die 3-D Grafik[Bearbeiten]

Hinweis:

Dieser Artikel soll Ihnen helfen, sich leichter in Blender zurechtzufinden, indem er ein paar wichtige grundlegende Begriffe erklärt und einen kleinen Einblick ermöglicht. Für die ungeduldigen oder diejenigen, die erstmal nicht tief in die Materie eintauchen möchten...

Im dreidimensionalen Raum wird jedes Objekt von drei Koordinaten - von drei Vektoren beschrieben. Legt man dem lateinischen Wort Vektor seine Übersetzung - Träger - zugrunde, wird die Bedeutung klarer. Ein Vektor ist ein Träger, in unserem Fall meistens ein Träger von Informationen. In Form von Vektoren werden in der Computergrafik Orte im Raum, Punkte oder Richtungen dargestellt (z.B ein Pfeil mit Länge und Richtung. Die Länge beschreibt die Stärke des Effekts).

X (Länge), Y (Breite) und Z (Tiefe) sind diese Koordinaten. Ein Objekt, das neben den drei Raumkoordinaten noch eine vierte Koordinate als Zeitachse besitzt, nennt man 4-D. Anstelle einer Zeitachse sind natürlich noch andere Angaben denkbar, z.B eine Gewichtung wie bei NURBS.

Körper sind ja in der Wirklichkeit aus Atomen aufgebaut. Atome bilden die Moleküle, Moleküle alle Stoffe. Aus denen wiederum alle Dinge bestehen. Da es jedoch zu kompliziert wäre, dies am Computer nachzuahmen, bedienen wir uns eines einfacheren Modells: Eine komplette 3-D Szene besteht aus einer Reihe von Objekten. Diese Objekte können in einzelne Bausteine aufgeteilt werden. Die Primitive (Sngl. Primitive). Primitive sind in der Grafik elementare Grundobjekte aus denen sich kompliziertere Objekte bauen lassen (2D: z.B Kreise, Linien...; 3-D: z.B triangels (Dreiecke), Würfel, Kugeln...). Solche Bausteine können aber auch NURBS (Non-Uniform Rational B-Spline) und Bézierkurven sein, siehe (Abb.2). Bei beiden handelt es sich um Kurven, die auf unterschiedlichen Mathematischen Modellen basieren. Im Gegensatz zu den Mesh(Polynetzen), die später erläutert werden, lassen sich mit diesen Kurven, leicht runde Objekte erzeugen. Sie sind nicht derartig facettiert und verbrauchen dabei auch weniger Rechenleistung. Mit ihnen lässt sich eine Vielzahl an Gegenständen nachbilden, was aber bisweilen einiges an "Know-how" erfordert. Objekte die miteinander agieren und verschmelzen sind sog. Metaobjekte. Leider sind sie eigentlich nur nützlich, wenn es um spezielle Anforderungen geht oder wenn sie als eine Grundlage für späteres Mesh Modelling dienen.

Andere Objekttypen

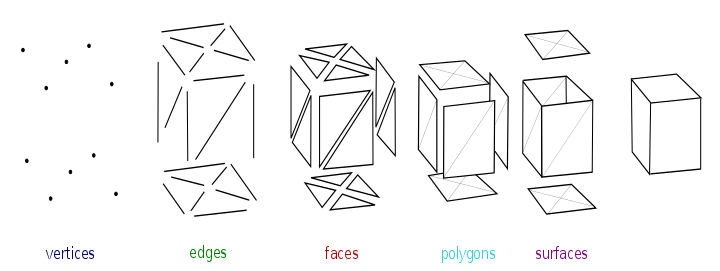
Im folgenden - wohl am wichtigsten und meist genutzten - das Mesh (engl. Netz; Polygonnetz): Elemente der Mesh Approximation (Annäherung).

Ein Mesh besteht aus sog. Vertices (singl. Vertex; engl. für Eckpunkt, auch Scheitelpunkt). Vertices sind nur Punkte im Raum, die Koordinaten auf der X-, Y- und Z-Achse besitzen. Ein Vertex kann aber auch Informationen wie Farbe oder Texturkoordinaten speichern. Werden zwei Vertices miteinander verbunden, ergibt dies ein Edge (engl. für Kante). Aus solche Kanten entstehen Flächen, sog. Faces . Oft spricht man auch von Facetten. Ein Face kann aus triangels oder quads bestehen. Also aus Dreiecken oder Vierecken, mit drei bzw. vier Vertices. Das ist insofern wichtig, als dass manche Dateiformate (z.B "3ds.") nur triangels unterstützten. Ein Mesh aus Dreiecken zu modellieren bietet sich an, wenn die einzelnen Primitive glatt und eindeutig definiert sein sollen. Außerdem sind Dreiecke immer planar, d.h alle Punkte befinden sich auf einer Ebene. Modelle die aus Quads bestehen sind übersichtlicher und für den Computer leichter weiterzuverarbeiten. Das Modellieren mit Dreiecksflächen wird auch Triangulierung genannt, das mit Vierecken auch Paving. Mehrere solcher Faces bilden ein Polygon(netz) (Vieleck). Das gilt - in der 3-D Grafik - auch für gekrümmte Oberflächen. Zwingend ist jedoch, dass ein Polygon immer geschlossen ist. Surfaces sind in sich geschlossene Einheiten eines Modells. smoothing groups sind Gruppen von geglätteten Vertices . Es hängt von der Ausrichtung der Normalen ab, ob diese Gruppen aus Vertices glatt erscheinen. Ein Mesh zu glätten ist erforderlich, da Meshes oft facettiert sind. Die Kanten bzw. Facetten eines Mesh können auch in Abhängigkeit von der Größe ihrer Winkel zueinander geglättet werden. Normalen sind Vektoren, die die Ausrichtung des Vertex bzw. Faces bestimmen. Was folglich bestimmt, ob und wie eine Fläche vom Licht bestrahlt wird. Da die Normalen bestimmen wie ein Objekt vom Licht bestrahlt wird (siehe Abb. 4), muss man darauf achten wie sie ausgerichtet sind und sie ggf. neu ausrichten. Die Verteilung der Normalen kann auch durch eine sog. Normalmap gesteuert werden. Eine Normalmap speichert in den Farben Rot, Grün und Blau die X, Y und Z Koordinaten der Normalen. Die jeweiligen Farbwerte (0-255) entsprechen den Werten der Normalen (-1.0 - 1.0). Solche Normalmaps kann man entweder mit einem Plug-In für Bildbearbeitungsprogrammen erzeugen ( z.B "NVIDIA Photoshoph Plug-in" oder "Gimps Normalmap Plug-In") oder 'backt'(baking) sie aus Highpoly Modelle (detailliert, aber viele Vertices) auf Lowpoly Modelle (niedriger Polycount, wenige Vertices). Ebenso lassen sie sich einfach von Hand malen. Welche Methode man benutzt sollte, je nach gewünschtem Ergebnis, neu entschieden werden. Wie ein Material Licht reflektiert und wie es schattiert ist, wird aber nicht nur von der Normalmap bestimmt. Shader sind ein Beleuchtungsmodell. In der 3-D Grafik werden Shader für Diffuse-Reflexion (Lichtstreuung, siehe Abb. 5) z.B "Lambert" und Shader für Glanzlichter (Reflexion von Licht) z.B "Blinn" benutzt.

Abbildung 1: NURBS
Abbildung 2: Bézierkurven
Abbildung 4: Helle und dunkle Bereiche aufgrund der Normalenverteilung
Abbildung 5: Diffuse Reflexion
Abbildung 6: Vergleich zwischen einem Model einmal ohne Textur (1) und einmal mit Textur (2)

Texturen sind Bilder, die den Objekten Eigenschaften, wie Farbe, Lichtreflexion, Transparenz oder Struktur, verleihen. Wie eine solche Textur auf einem Objekt angeordnet wird, nennt man Texture Mapping (Musterabbildung). Um die Texturen richtig zu positionieren gibt es unterschiedliche Techniken. Die Koordinaten können beispielsweise auf Objekt- oder Szeneeigenschaften beruhen (Normalen, Bildschirmkoordinaten...). Oft genutzt werden Koordinaten die vom Objekt selbst bzw. der das Objekt umgebenden Bounding Box (siehe Abb. 7; oft stehen sie anstelle des Objekts, welches sie umschließen, um Übersichtlichkeit oder höhere Performance zu erreichen. Sie werden auch Bounding Volume gennant). Sehr präzise ist das UV Unwrapping, bei dem ein Objekt auseinander gefaltet wird (siehe Abb. 8). Anschließend wird es auf die Texture gemappt. Erwähnenswert sind noch Prozentuale Texturen, die durch einen Algorithmus vom Computer errechnet werden. Sie sind also beliebig skalierbar. Im Gegensatz zu Texturen, die auf Rastergraphik basieren. Bei weit entfernten Objekten, ist der hohe Detailgrad der Texturen nicht zu erkennen. Die Rechenleistung, die erforderlich war, ist also überflüssig. Schlimmstenfalls (was relativ oft der Fall ist) treten Moiré-Effekte oder Aliasing (Treppchen) auf. Um dem entgegenzuwirken, werden seit 1983 MIP-Maps verwendet. MIP-Maps sind unterschiedlich detaillierte Versionen der Haupttextur. Der Grad an Details hängt von der Entfernung zur Kamera ab. Viele Details, wenn sich die Textur nahe an der Kamera befindet. Wenige Details, wenn das Objekt weit entfernt ist. Dies wird als LOD (Level of Detail) bezeichnet. Die meisten 3-D Programme errechnen sie automatisch. Um zum Beispiel in Echtzeit-Simulationen mehr Geschwindigkeit zu erhalten, können die MIP-Maps auch heruntergerechnet werden. Dies geschieht durch einen Gauss-Filter. Der Moiré-Effekt tritt bei der Überlagerung von Rastern und Linien auf,z.B wenn periodisch wiederholenden Muster z.B karierte Hemden gefilmt, gescannt oder fotografiert werden. Deswegen trägt auch kaum jemand im Fernsehen stark karierte Hemden oder Jacketts. Wenn sie jedoch mit eine Digital Kamera ein Bild von einem Fernsehbildschirm nehmen, können sie den Moiré-Effekt sehen, der durch das Farbraster ensteht. Aliasing oder der Treppeneffekt (siehe Abb. 12) tritt an den Kanten gerasteter Bilder auf (engl. Jaggies; ganz genau genommen handelt es sich hierbei nämlich nicht um Aliasing, trotzdem weiß jeder was damit gemeint ist). Der Treppeneffekt tritt auch beim Druck auf, wird dort aber Sägezahneffekt genannt. Folge sind ausgefranste Kanten (z.B U, O oder P ). Im weiteren gibt es Techniken bzgl. Anti-Aliasing (z.B OSA <-> Oversampling), die den Treppeneffekt vermindern sollen (siehe Abb. 13). Rasterung bezeichnet den Vorgang bei dem Vektorgrafik (dreidimensionale Vektorgrafik bezeichnet man eher als Szene oder 3-D Modell) in auf Pixel basierte Rastergraphik. Diesen Vorgang bezeichnet man als Rendern (engl. berechnen). Diese Berechnung, auch Bildsynthese (nur bei 3-D) genannt, wird entweder in Echtzeit gerendert (z.B Computerspiele oder Blenders Viewport (Darstellungsfeld)) oder aber aufwendiger und länger, was sehr photorealistische Ergebnisse erzielen kann. Bei ersteren ist Geschwindigkeit entscheidend, weshalb mit einer Reihe von Tricks versucht wird, einen guten Kompromiss aus Rechenaufwand und Effekten zu erzielen. Beide enthalten Effekte wie Anti-Aliasing, Lichteffekte, Materialien und Textur in unterschiedlicher Qualität. Die höchste Qualität erzeugen die sog. Raytracer deren Modelle von Lichtreflexion, beeindruckende Resultate erzielen. Yafaray oder LUX sind solche Raytracer. Blenders Interner Render verwendetet ein vereinfachteres Modell zur Lichtreflexion. Ein Vorteil davon ist die höhere Rechengeschwindigkeit.

Abbildung 7: Bounding Box
Abbildung 8: UV Unwrapping (Abwickeln)
Abbildung 9: Ausgangsbild
Abbildung 10: Moiré-Effekt
Abbildung 11: Entstehung des Moiré-Effekt.
Abbildung 12: Treppeneffekt
Abbildung 13: Oben ohne Anti-Aliasing, unten mit Anti-Aliasing

weiterführende Lektüre[Bearbeiten]

Deutschsprachige

Digital Media for Artists (E-Learning Projekt der Universität Linz. Besteht aus einzelnen Modulen, die das wichtige verständlich erklären. Behandelt neben 3-D noch weiteres wie DTP)

Bildsynthese

Englischsprachige Guerrilla CG (leicht verständliche Videotutorials über Grundlagen) Tech Artists Wiki (Ausführliche Artikel, Website im Wikiformat)

Vektoren[Bearbeiten]

Punkte, Koordinaten und Vektoren!

Übersicht

Mit Vektoren lassen sich die Lage von Punkten oder deren Verschiebung innerhalb eines Raumes angeben.

Ein Vektor ist eine gerichtete Strecke, die Größe ("Länge") bezeichnet man als Skalar.
Ein Vektor beginnt im Ursprung eines Koordinatensystems, zeigt in eine eindeutige Richtung, und endet an einem Punkt.
Um einen Vektor zu definieren zerlegt man ihn in seine Komponenten.

Komponentendarstellung

Die Komponentendarstellung von Ortsvektoren ist gar nicht so schwierig, wie es vieleicht auf den ersten Blick aussehen mag.

1 Der Vektor beginnt im Ursprung des Koordinatensystems und endet im Punkt A.

2 Die Projektion des Vektors auf ein Koordinatensystem ergibt die vektoriellen Komponenten des Vektors bzw. die Koordinaten des Punktes A sog. Punktkoordinaten :

.

3 Die Vektorielle Komponente des Vektors auf der Z-Achse ist . Der Skalare Komponent demnach: Für die X- und Y-Achsen verhält es sich natürlich entsprechend.

Übrigens ein solches Koordinatensystem, wie nebst dargestellt, nennt man rechtwinkliges (kartesisches) Koordinatensystem. Die X-Achse wird dort auch Abszisse, die Y-Achse Ordinate und die Z-Achse Applikate bzw. in der Geographie Kote (Höhenpunkt) genannt.

Über Primitive und Aufbau von Körpern in der 3D CG

In der Grafik arbeitet man häufig mit Primitiven. Primitive sind Grundformen. Grafisches Primitiv in der zweidimensionalen Grafik ist ein Punkt, das Quadrat oder der Kreis, in der dreidimensionalen ein Würfel oder eine Kugel. Aus solchen Primitiven lassen sich komplexere Objekte bilden.

Körper sind ja in der Wirklichkeit aus Atomen aufgebaut. Atome bilden die Moleküle, Moleküle alle Stoffe. Aus denen wiederum alle Dinge bestehen. Da es jedoch zu kompliziert wäre, dies am Computer nachzuahmen, bedienen wir uns eines einfacheren Modells: Eine komplette 3-D Szene besteht aus einer Reihe von Objekten. Solche Objekte bestehen letztendlich immer aus Polygonalen Netzen. Es sind Netze mit vielen Ecken (Polygon: Vieleck). Eine Solches Eck bezeichnet man häufig mit seiner englischen Entsprechung Vertex (Pl. Vertices). Werden zwei Vertices miteinander verbunden bilden sie eine Kante, ein Edge . Mindestens drei Vertices miteinander verbunden, bilden eine Facette oder Face (es entsteht ein Dreieck, Dreiecke sind immer planar d.h flach!).

Beim Meshing nähert man sich der Form eines Körpers durch viele kleine Elemente an. Die Elemente der Mesh Approximation (Annäherung) haben wir ja eben kennen gelernt. Das Modellieren mit Dreiecksflächen wird auch Triangulierung genannt, das mit Vierecken Paving.

Wenn´s mal schief geht. Über Bildfehler.

Aliasing

Aliasing ist die Verfremdung von analogen Signalen, die bei deren Digitalisierung auftreten. Während Analoge Signale kontinuierlich sind, d.h beliebig viele Zwischenwerte annehmen können, kennt ein digitales Signale nur die Werte 1 und 0. Weswegen Übergänge bei der Digitalisierung verloren gehen.

Moiré-Effekt

Der Moiré-Effekt tritt bei der Überlagerung von Rastern und Linien auf,z.B wenn periodisch wiederholenden Muster z.B karierte Hemden gefilmt, gescannt oder fotografiert werden. Deswegen trägt auch kaum jemand im Fernsehen stark karierte Hemden oder Jacketts. Wenn sie jedoch mit eine Digital Kamera ein Bild von einem Fernsehbildschirm nehmen, können sie den Moiré-Effekt sehen, der durch das Farbraster ensteht.

A. Ausgangsbild
B. Moiré-Effekt tritt auf weil das Bild nicht im erforderlichen Maße heruntergerechnet wurde.
Grafik

Treppeneffekt

Der Treppeneffekt tritt an den Kanten gerasteter Bilder auf (engl. Jaggies). Um den Effekt zu vermindern benutzt man OSA <-> Oversampling.

In

Anti-Aliasing

Oversampling Das Oversampling ist eine direkte Antwort auf den Treppeneffekt. Oversampling ist eine Überabtastung, will heißen auf Subpixel Niveau. Anstatt lediglich einer Probe (Sample) von jedem Pixel zu nehmen, wird der Bereich eines Pixel mehrmals getestet, um herauszufinden wie stark es gefüllt ist.

Normalmaps

Flächennormalen sind senkrecht auf einer Fläche stehende Vektoren. Eben diese Flächennormalen, die ein Vektor sind, werden, in ihre X , Y und Z Komponenten zerlegt und in einer Normalmap abgespeichert. Die Vektoren werden also in Rot-, Grün-, Blauwerten codiert. Eine Normalmap speichert also Normalen und damit auch die Winkel in denen Flächen zueinander stehen. Da Normalen zur Berechnung der Schattierung herangezogen werden, bieten Normalmaps viel Potenzial die Schattierung von Objekten zu beeinflussen. Es lassen sich also nicht vorhandene Details simulieren.

Solche Normalmaps kann man entweder mit einem Plug-In für Bildbearbeitungsprogrammen erzeugen ( z.B "NVIDIA Photoshoph Plug-in" oder "Gimps Normalmap Plug-In") oder 'backt'(baking) sie aus Highpoly Modelle (detailliert, aber viele Vertices) auf Lowpoly Modelle (niedriger Polycount, wenige Vertices). Ebenso lassen sie sich einfach von Hand malen. Welche Methode man benutzt sollte, je nach gewünschtem Ergebnis, neu entschieden werden.

Beleuchtung und Shading[Bearbeiten]

Beleuchtung[Bearbeiten]

Beleuchtung beleuchtet eine Szene. Es wird zwischen lokaler und globaler Beleuchtung unterschieden. (3-D Prozess)

lokale Beleuchtung	globale Beleuchtung
beachtet nur direkt einfallendes Licht (kein Schattenwurf!)	beachtet auch indirekt einfallendes Licht (Reflexion, Transmission)
z.B Phong Beleuchtungsmodell; Lamberts	z.B Raytracing; Radiosity

Shading[Bearbeiten]

Beim Shading wird berechnet wie eine Fläche beleuchtet wird.

Flat Shading (Lambert-Shading) Aus der Flächennormale wird die Schattierung der gesamten Facette berechnet. Dieses Verfahren ist sehr schnell, aber die einzelnen Facceten sind noch sichtbar.

Gouraud-Shading Schattierung wird in den Eckennormalen berechnet, dann für die Facette ein Farbverlauf zwischen den Ecknormalen interpoliert. Gouraud-Shading interpoliert also Farwerte. Der Nachteil ist, dass Highlights auf einer Facette durch die Interpolation verloren gehen können.

Phong Shading Schattierung eines Pixels wird aus dem entsprechenden Objektpunkt (z.B der Punkt B) berechnet, die dazu erforderliche Normale und deren Ausrichtung wird aus den Eckennormalen interpoliert.

Blinn-Shading Ähnelt dem Phong-Shader, bei der Berechnung wird jedoch noch ein Brechungsindex ermittelt. Was genauere Highlights bei starken Krümmungen ermöglicht. 3D-Grafik-Software bietet in der Regel auch einen Regler um den Brechungsindex einzustellen. Blinn-Shading (auch Blinn-Phong-Shading) wird auch standardmäßig in OpenGL und Direct3D verwendet.