Benutzer:Oceancetaceen = Alice/ Schulbücher 2.0/ Mathematikunterricht/ Quadratische Gleichungen
Funktionen der Form y = ax² + bx + c heißen quadratische Funktionen. Ihre Graphen sind parabelförmig.
Die Normalparabel (y = x²)
[Bearbeiten] Der Graph der Funktion y = x² (a=1; b=0; c=0) heißt Normalparabel. Sie ist nach oben geöffnet, hat ihren Ursprung im Punkt (0|0) und die Y-Achse ist die Symmetrieachse dieser Parabel.
Der Graph der Funktion y = x² (a=1; b=0; c=0) heißt Normalparabel. Sie ist nach oben geöffnet, hat ihren Ursprung im Punkt (0|0) und die Y-Achse ist die Symmetrieachse dieser Parabel.
Quadratische Funktionen der Form y = ax² + c
[Bearbeiten]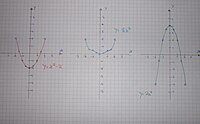 Parabel nennt man den Graphen der Funktion Y = ax² + c.
Die Konstanten a und c verändern Lage und Form der Normalparabel.
Parabel nennt man den Graphen der Funktion Y = ax² + c.
Die Konstanten a und c verändern Lage und Form der Normalparabel.
- Der Faktor a bestimmt die Form und Öffnung der Parabel.
- Der Summand c bestimmt die Länge und Richtung, der Verschiebung auf der Y-Achse.
|a| > 1 = schlanker |a| < 1 = breiter a > 0 = nach oben geöffnet a < 0 = nach unten geöffnet
Rein quadratische Gleichungen (ax2 + c = 0)
[Bearbeiten]Zeichnerische Lösung
[Bearbeiten]- 1.) Den Graphen zeichnen/ zeichne die Funktion y = ax2 + c
- 2.) An den Nullstellen des Graphen ist Y =0, also 0 = ax2 + c
- 3.) Die Nullstellen der Funktion y = ax2 + c sind die Lösungen der Gleichung ax2 + c = 0
Rechnerische Lösung
[Bearbeiten]Rein quadratische Gleichungen löst man durch das Zerlegen in die Linearfaktoren mit der 3. binomischen Formel. Steht vor x² ein Faktor, so muss erst durch diesen Dividiert werden.
Gemischt quadratische Gleichungen Y = ax2 + bx + c
[Bearbeiten]Nach Umformen der Funktion y = ax2 + bx + c in die Scheitelform y = a(x + d)2+e lässt sich der Scheitelpunkt S (-d|e) der Parabel ablesen. Das Vorzeichen von d wird umgekehrt. Weil man die binomischen Formeln anwenden muss, ist eine quadratische Ergänzung nötig.
Beispiel:
Y = 2x2 + 12x + 22 |Faktor vor X ausklammern = 2( x2 + 6x + 11) = 2( x2 + 2·3x + 3² + 11) = 2[(x + 3)2 + 2] = 2( x + 3)2 + 4 Der Scheitelpunkt dieser Gleichung ist S(-3|4)
Lösungsformel
[Bearbeiten]Um heraus zu finden, welche X-Werte die Gleichung ax² + bx + c = 0 muss die Gleichung in die Normalform x² + px + q = 0 umgeformt werden, dazu muss sie durch den Faktor, der vor dem x² steht, geteilt werden.
Zeichnerische Lösung
[Bearbeiten]- 1.) Umformung in die Normalform
- 2.) Normalparabel mit ermittelten Scheitelpunkt zeichnen
- 3.) Die Nullstellen (y = 0) sind die Lösungen der Gleichungen
Rechnerische Lösung
[Bearbeiten]- 1.) Umformen in die Normalform x² + px + q = 0
- 2.) Lösungsformel verwenden:

