Benutzer:Stephan Kulla/ Spielwiese2
Das Integral als Durchschnittswert
[Bearbeiten]Wiederholung: Durchschnitt und gewichteter Durchschnitt
[Bearbeiten]Mit dem Integral kann der Durchschnittswert einer Funktion bestimmt werden. Bei verschiedenen Werten bis kann ihr Durchschnitt bzw. der Mittelwert bestimmt werden über
So ist der Durchschnitt der Werte gleich . Wenn die einzelnen Werte bis in der Berechnung des Durchschnitts durch unterschiedliche Faktoren bis gewichtet werden sollen, lautet die Formel:
Eine Gewichtung bedeutet beispielsweise, dass der Wert doppelt so stark in den Durchschnitt eingehen soll, als wenn wäre.
Durchschnittsberechnung einer Funktion
[Bearbeiten]Eine Funktion hat unendlich viele Argumente und nimmt damit unendlich oft Funktionswerte an. Die Formel zur Mittelwertsberechnung von endlich vielen Werten kann also nicht verwendet werden, um den durchschnittlichen Funktionswert von zu bestimmen. Wir können diesen aber annähern. Hierzu zerlegen wir das Intervall in Teilintervalle. Durch die Wahl von Stützstellen mit und wird das Intervall in Intervalle mit unterteilt:

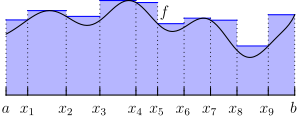
Sei nun das Supremum und das Infimum der Funktionswerte von im Teilintervall . Damit das Supremum und Infimum existiert, nehmen wir zusätzlich an, dass beschränkt ist. Nun können zwei Treppenfunktionen definiert werden, die jeweils die Funktion von oben bzw. von unten annähern. Bei der oberen Treppenfunktion definieren wir für und . Bei der unteren Treppenfunktion ist bei und :
-
Treppenfunktion , die die Funktion von unten approximiert.
-
Treppenfunktion , die die Funktion von oben approximiert.
Beide Treppenfunktionen nehmen nur endlich viele Werte an und nähern beide den Funktionsverlauf von an. Da die Werte von immer über den Werten von liegen, sollte auch der durchschnittliche Wert von größer gleich dem Mittelwert von sein. Der Durchschnittswert der oberen Treppenfunktion schätzt also den gesuchten Funktionsmittelwert nach oben ab. Analog ist der Durchschnittswert der unteren Treppenfunktion eine Abschätzung nach unten für den Mittelwert von .
Um den Mittelwert einer Treppenfunktion zu bestimmen, reicht es nicht aus, den Durchschnitt der angenommen Funktionswerte zu bilden. So nehmen die folgenden Treppenfunktionen dieselben Funktionswerte an. Wegen der unterschiedlichen Größe der Teilintervalle sollte sich auch der Durchschnittswert der beiden Teilintervalle unterscheiden:
-
Treppenfunktion mit den Werten , und . Der durchschnittliche Wert sollte aber größer als sein.
-
Auch diese Treppenfunktion nimmt nur die Werte , und an. Ihr durchschnittlicher Wert sollte aber geringer als sein.
Vielmehr müssen wir die Funktionswerte mit den Längen der Teilintervalle gewichten, wo diese Funktionswerte angenommen werden. Das -te Teilintervall hat die Länge . Bei der oberen Treppenfunktion bilden wir also den Mittelwert der Zahlen mit den Gewichten :
Analog können wir den Durchschnittswert der unteren Treppenfunktion bestimmen. Insgesamt erhalten wir die Abschätzung:
Wir konnten also den durchschnittlichen Funktionswert der gegebenen Funktion abschätzen. Als Summen treten dabei die Ober- und Untersummen auf, die selbst den orientierten Flächeninhalt unter dem Graphen approximieren. Um die obige Abschätzung weiter zu verbessern, müssen wir das Grundintervall immer feiner zerlegen. Unter der Voraussetzung, dass die Funktion riemannintegrierbar ist, strebt dabei die Unter- sowie die Obersumme gegen das Integral . Mit Hilfe des Sandwichsatzes können wir aus obiger Abschätzung folgern:
Mit Hilfe des Integrals kann also der Durchschnittswert einer Funktion bestimmt werden. Hierzu muss das Integral durch die Länge des Grundintervalls geteilt werden.














![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



![{\displaystyle [x_{k-1},x_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f77539e232b976d1a83e1829624235bba4164757)



![{\displaystyle T:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c34f514a9e2ced1f18e8ea5f753c6c4aede92d66)



![{\displaystyle t:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/efbb2e7af4f8d80215b3b0b3ac7698eac642ae9b)










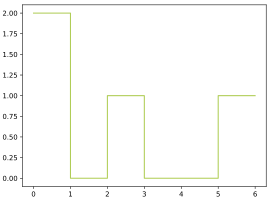



![{\displaystyle {\begin{aligned}{\overline {T}}&={\frac {M_{1,n}\cdot (x_{1}-x_{0})+M_{2,n}\cdot (x_{2}-x_{1})+\ldots +M_{n,n}\cdot (x_{n}-x_{n-1})}{(x_{1}-x_{0})+(x_{2}-x_{1})+\ldots +(x_{n}-x_{n-1})}}\\[0.5em]&={\frac {\sum _{k=1}^{n}M_{k,n}\cdot (x_{k}-x_{k-1})}{x_{n}-x_{0}}}={\frac {1}{b-a}}\cdot \sum _{k=1}^{n}M_{k,n}\cdot (x_{k}-x_{k-1})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11dde1422038418cb2f6c4830d23ca8a02695de4)





