C++-Programmierung/ Eine Matrix-Bibliothek – mitrax

Eine Matrix-Bibliothek – mitrax

Zielgruppe:

Fortgeschrittene / Profis

Lernziel:
Im Verlauf dieses Kapitels wird eine Bibliothek zum Arbeiten mit Matrizen von Grund auf entwickelt. Dabei werden mehrere fortgeschrittene Programmiertechniken eingesetzt und erläutert. Es wird außerdem umfassend auf die Bedürfnisse potentieller späterer Nutzer der Bibliothek eingegangen, so dass Sie ein Gespür dafür entwickeln können, auf welche Punkte im Allgemeinen geachtet werden muss, wenn man Schnittstellen für andere Programmierer entwickelt.

In diesem Abschnitt werden die folgenden Verzeichnisse und Dateien entstehen:

• mitrax.hpp
• mitrax/
  • dimension.hpp
  • matrix.hpp
  • proxy.hpp
  • detail/
    • proxy_iterator.hpp
  • io.hpp
  • iomanip.hpp
  • exception.hpp
  • simple_operator.hpp
  • operator.hpp

Zielstellung

In diesem Kapitel wollen wir eine Bibliothek zum Arbeiten mit Matrizen entwickeln. Bei dieser Gelegenheit werden einige fortgeschrittene Programmiertechniken vorgestellt. Außerdem soll der Leser einen ersten Eindruck gewinnen, was bei der praktischen Entwicklung beachtet werden muss. Wenn Sie Schwierigkeiten haben sollten, den Werdegang nachzuvollziehen, dann sollten Sie sich möglicherweise die vorangegangen Kapitel noch einmal genauer anschauen, da hier nicht mehr auf jede Kleinigkeit hingewiesen wird. Dies ist notwendig, um den Text kompakt und übersichtlich zu halten, denn sonst werden sich Leser, welcher der fortgeschrittenen Zielgruppe dieses Kapitels angehören, unnötig langweilen und möglicherweise wichtige Hinweise zur eigentlichen Problemstellung überlesen. Alle Bestandteile von mitrax sollen im Namensraum mitrax stehen. Darauf wird in den folgenden Kapiteln jedoch ebenfalls nicht mehr explizit hingewiesen.

mitrax – Namensherkunft

Mitra Mitra aus der Gattung der Mitra

Das Projekt mitrax entstand als Semesterarbeit. Die Aufgabenstellung lautete in groben Zügen, man entwickle eine Klasse welche Matrizen (im mathematischen Sinne) repräsentiert. Dabei sollten insbesondere einige Rechenoperatoren überladen werden und die Klasse sollte als Template, unabhängig vom konkreten Typ ihrer Elemente, nutzbar sein. Da sich während der Entwicklung herauskristallisierte, dass sich das Ergebnis hervorragend als Lehrbeispiel eigenen würde, entstand parallel auch dieser Abschnitt.

Der Name „mitrax“ entstand durch zufälliges Vertauschen der Buchstaben von „matrix“. Dadurch ergibt sich, nach Entfernen des Buchstabens „x“ am Ende, ein Wort, das in der Biologie eine Gattung innerhalb der Familie der Mitridae (auch Mitraschnecken genannt) bezeichnet. Da deren Gestalt zwar immer ähnlich und dennoch abwechslungsreich ist, erinnern diese Tiere ein wenig an den Templatecharakter der Matrixklasse, auf den ja besonderen Wert gelegt wurde.

Konkretisierung der Aufgabenstellung

In einem realen Entwicklungsprozess würde dieser Schritt gemeinsam mit dem Auftraggeber erfolgen. Da in unserem Fall jedoch kein solcher existiert, werden wir selbst festlegen, was sinnvollerweise möglich sein sollte.

Schema für eine allgemeine m×n-Matrix

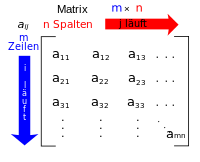
Zunächst machen wir uns Gedanken darüber, was eine Matrix eigentlich ist. Im wesentlichen handelt es sich dabei um rechteckige Anordnung von Elementen gleichen Typs. Sie enthält also eine Information über die Anzahl der Zeilen und die Anzahl der Spalten, sowie Anzahl Zeilen mal Anzahl Spalten viele Elemente des gleichen Typs. Die Anzahl der Zeilen und Spalten wird als Dimension der Matrix bezeichnet. Im deutschen spricht man in diesem Zusammenhang eigentlich vom Typ der Matrix, dieser Begriff würde jedoch ständig zu Verwechslungen mit C++-Typen führen, daher werden wir den Begriff Typ in diesem Abschnitt nicht verwenden.

Nun ist es Sinnvoll, wenn einzelne Zeilen und Spalten herausgegriffen werden können. Ein Zugriff auf ein konkretes Element sollte natürlich auch möglich sein. Diese Zugriffe werden wir mittels sogenannter Proxyklassen realisieren. Dies hat auch den Vorteil, dass der Zugriff auf einzelne Elemente, wie bei einem zweidimensionalen Array, durch zweimalige Anwendung des Indexoperators (operator[]()) durchgeführt werden kann.

Für viele Operationen ist die konkrete Anordnung eines Elements im Rechteck unwesentlich, da lediglich alle Elemente innerhalb der Matrix einmal verarbeitet werden müssen. Aus diesem Grund werden wir ein Iteratorinterface für die Matrixklasse und auch für die Proxyklassen anbieten. Die Nutzung von Iteratoren gibt einem Leser von Quellcode auch immer den Hinweis, dass es sich hier um eine elementweise Verarbeitung von Elemente handelt. Wir erhöhen somit potenziell die Lesbarkeit von Clientquellcode, also dem, was ein Nutzer unserer Bibliothek schreibt. Natürlich gilt dies ebenso für den Quellcode unserer Bibliothek, wenn wir das Iteratorinterface irgendwo nutzen.

Auf Matrizen können verschieden Rechenoperationen definiert werden. Wir wollen uns dabei auf die folgenden beschränken:

• Negation einer Matrix
• Addition / Subtraktion zweier Matrizen gleicher Dimension
• Multiplikation mit einem Skalar
• Division durch einen Skalar
• Matrixmultiplikation
• Transponieren
• Für quadratische Matrizen:
  • Determinante
  • Inverse Matrix

Diese Rechenoperationen werden nicht als Member der Matrixklasse implementiert, da sie nicht zu einer Matrix gehören, sondern auf Matrizen arbeiten. Sie werden also als nicht befreundete Nichtelementfunktionen deklariert. Dies hat nebenbei den gewaltigen Vorteil, dass ein Nutzer von mitrax selbst weitere Operationen im gleichen Stil schreiben kann. Syntaktisch wird in seinem Quellcode dann nicht direkt zu erkennen sein, ob es sich um eine native (von uns bereitgestellte) Funktion oder um eine selbst definierte handelt, was die Lesbarkeit seines Quellcodes erhöht. Einen Leser seines Codes würde es nur unnötig verwirren, wenn zwei anscheinend gleichberechtigte Operationen unterschiedlich aufgerufen werden müssten. Außerdem entspricht es auch dem Paradigma der objektorientierten Programmierung, das Funktionen, die keinen direkten Zugriff auf die internen Elemente einer Klasse benötigen, auch keinen haben. Die Daten sind dadurch stärker gekapselt.

Vielleicht ist ihnen bekannt, dass viele der Operationen auf Matrizen nur unter bestimmten Voraussetzungen ausgeführt werden können. So müssen beispielsweise zwei Matrizen, die addiert werden sollen, die gleiche Dimension besitzen. Anhand der Liste der Operationen, die wir definieren möchten, wird aber auch schon offensichtlich, dass bestimmte Operationen nur für quadratische Matrizen ausführbar sind, also solche, die die gleiche Anzahl von Zeilen und Spalten besitzen. Das führt uns dazu, dass wir eine ganze Reihe eigener Klassen zur Ausnahmebehandlung benötigen. Es wird zwar versucht, das Thema getrennt in einem eigenen Kapitel zu behandeln, jedoch treten in vielen Kapitel Situationen auf, für die eine Ausnahmebehandlung nötig ist. Daher sind hier einige Querverweise unumgänglich. Lassen Sie sich davon bitte nicht verwirren. Wenn Sie einen Hinweis zu diesem Thema an einer bestimmten Stelle noch nicht verstehen, dann lesen Sie erst mal weiter, in den meisten Fällen sollte irgendwann klar werden, was gemeint war.

Um etwas von unseren Matrizen zu sehen, benötigten wir natürlich eine Ein- und Ausgabe. Bei dieser Gelegenheit werden auch gleich ein paar eigene Manipulatoren für die Ausgabe einer Matrix bereitstellen. Das Format für die Ein- und Ausgabe sollte immer identisch sein, so dass wir eine ausgegebene Matrix auch später wieder einlesen können. Allerdings kann bei der Ausgabe mittels Whitespaces die Übersichtlichkeit für einen menschlichen Betrachter deutlich erhöht werden. So können etwa die einzelnen Elemente mit einer festen Mindestbreite ausgegeben werden. Auch eine zweidimensionale Ausgabe kann auf diesem Weg an und abgeschaltet werden. Es muss lediglich sichergestellt sein, dass der Eingabeoperator mit jeder möglichen Ausgabe zurechtkommt. Für die Proxyklassen werden wir ein eigenes Format festlegen.

Zum Abschluss möchten wir die Berechnungen noch einmal überarbeiten, so dass Sie verzögert ausgeführt werden. Das hat mehrere wesentliche Vorteile in Bezug auf die Performance. Zum einen müssen Berechnungen, deren Ergebnis nicht verwendet wird, auch niemals ausgeführt werden. Das ist gar nicht so selten der Fall, wie Sie vielleicht vermuten werden. Der zweite Vorteil besteht darin, dass längere Berechnungsketten in einem Durchlauf abgearbeitet werden können, anstatt für jede Operation ein eigenes temporäres Objekt anzulegen. Das spart Zeit und Speicherplatz. Als letzter Punkt wäre aufzuführen, dass die Prüfung der Dimensionskompatibilität für längere Berechnungsketten vorweg ausgeführt werden kann. Wenn ein Fehler festgestellt wird, dann beschwert sich das Programm sofort darüber und führt nicht erst Berechnungen von Zwischenergebnissen durch, die am Ende sowieso nicht weiterverarbeitet werden können. Das wird den Nutzern von mitrax vor allem in der Entwicklungsphase helfen, nicht unnötige Mengen von Kaffee zu konsumieren, während der Rechner arbeitet, nur um dann festzustellen, dass alles nochmal ausgeführt werden muss, weil sich am Ende ihres Programms ein logischer Fehler eingeschlichen hat.

Dimension einer Matrix

Die Inhalte dieses Kapitels werden in der Datei dimension.hpp stehen. Die Dimension einer Matrix besteht aus einer Anzahl von Zeilen und Spalten. Ein entsprechender Datentyp soll nichts weiter tun, als diese in einen Zusammenhang zu bringen. Der Lesezugriff soll auf die Anzahl der Zeilen und der Spalten getrennt möglich sein, während der Schreibzugriff immer beide betreffen sollte. Das Erstellen von Objekten muss natürlich entweder ohne Argumente oder mit einer Anzahl von Zeilen und eine Anzahl von Spalten möglich sein. Außerdem bietet es sich an, eine Erstellung aus Objekten zu ermöglichen, die ebenfalls über eine Höhe (Anzahl von Zeilen) und eine Breite (Anzahl von Spalten) verfügen. Ein Kopierkonstruktor ist selbstverständlich auch notwendig, wobei hier die vom Compiler erstellte Variante genutzt werden sollte. An dieser Stelle gibt es noch keine Notwendigkeit, sich auf einen bestimmten Typ für die internen Größen festzulegen. Lediglich dass dieser für Zeilen und Spalten identisch sein sollte, kann schon sicher gesagt werden. Alles in allem sieht unsere Klasse damit folgendermaßen aus:

template < typename T >
class dimension{
public:
    // Clientklassen müssen herausfinden können, welchen Typ die Daten haben
    typedef T value_type;

    // Konstruktoren
    dimension():
        rows_(value_type()),
        columns_(value_type())
        {}

    dimension(value_type const& rows, value_type const& columns):
        rows_(rows),
        columns_(columns)
        {}

    template < typename SizeType >
    explicit dimension(SizeType const& size):
        rows_(size.height()),
        columns_(size.width())
        {}

    // Schreibzugriff
   void resize(value_type const& rows, value_type const& columns){
        rows_ = rows;
        columns_ = columns;
    }

    // Lesezugriff
    value_type const rows()const{return rows_;}
    value_type const columns()const{return columns_;}

private:
    value_type rows_;
    value_type columns_;
};

Schauen wir uns die Bedingungen, unter denen die verschiedenen Methoden genutzt werden können, noch einmal genauer an. Für die Nutzung des Standardkonstruktors muss value_type (also der als Templateparameter übergebene Typ T) defaultkonstruierbar sein. In den meisten Fällen dürfte value_type für einen eingebauten Datentyp stehen. Diese sind alle defaultkonstruierbar und entsprechend kann der Standardkonstruktor mit Ihnen verwendet werden. Beachten Sie an dieser Stelle noch einmal, dass dies explizite Initialisierung für eingebauten Datentypen, nicht äquivalent zu einem Konstruktor ist, der keine explizite Initialisierung der Datenmember durchführt. Der Grund hierfür ist in einem früheren Kapitel dieses Buches beschrieben.

Der zweite Konstruktor setzt voraus, das value_type kopierkonstruierbar ist. Damit der Compiler einen Kopierkonstruktor für dimension-Objekte erzeugen kann, muss diese Bedingung ebenfalls erfüllt sein.

Der dritte Konstruktor ist ein Template. Er übernimmt eine Referenz auf ein konstantes Objekt vom Typ SizeTyp. Damit dieser Konstruktor genutzt werden kann, müssen SizeTyp-Objekte über die Methoden width() und height verfügen. Diese Methoden müssen konstant sein und sie müssen Objekte von einem Typ zurückgeben, der implizit in value_type gewandelt werden kann. Das bedeutet, dass value_type-Objekte entweder einen Konstruktor besitzen, der ein SizeTyp-Objekt übernimmt, oder kopierkonstruierbar sein müssen, wobei SizeTyp dann einen Castoperator nach value_type zur Verfügung stellen muss. Sind beides eingebaute Datentypen, so ist eine implizite Umwandlung natürlich immer möglich. Dass der Konstruktor explicit ist, ergibt sich aus der Tatsache, dass SizeTyp nicht zwingend auch einer Dimension oder allgemein einer 2D-Größe entspricht. Betrachten Sie folgendes Beispiel, in dem angenommen wird, der Konstruktor wäre nicht explicit:

dimension< std::size_t > dim1 = size();   // OK
dimension< std::size_t > dim2 = rect();   // Grenzwertig
dimension< std::size_t > dim3 = pixmap(); // Aussagemäßiger Blödsinn

size(), rect() und pixmap() stehen jeweils für Objekte der entsprechenden Typen. Was die Typen repräsentieren, ist für unsere Zwecke am Name ausreichend erkennbar. Sicher erinnern Sie sich noch, dass diese implizite Schreibweise für eine Initialisierung immer dann verwendet werden sollte, wenn man guten Gewissens sagen kann, dim1 entspricht dimension(). Für dieses erste Beispiel ist das ohne Bedenken möglich. dim2 entspricht einem rect() ist dagegen schon grenzwertig. Man kann es noch durchgehen lassen, aber aussagekräftiger wäre es, so etwas wie dim2 = rect().size() zu schreiben. dim3 entspricht einer pixmap() ist endgültig Blödsinn. Eine Pixmap ist etwas völlig anderes als eine 2D-Größenangabe.

Nutzt man nun stattdessen die Schreibweise der expliziten Initialisierung, dann wandelt sich die Aussage von „entspricht“ in „wird konstruiert aus/mit“. Für size() ist es jetzt zwar schade, dass man die implizite Schreibweise nicht verwenden kann, aber mit der jetzigen Aussage macht man auch nichts falsch. rect() kann mit dieser Schreibweise ebenfalls guten Gewissens zur Initialisierung verwendet werden, ohne dass sich der aufmerksame Leser fragen muss, was hier wohl passiert. Für pixmap() wäre es angemessen, stattdessen pixmap().size() zu schreiben, leider bieten nicht alle Typen auch eine Methode an, die Breite und Höhe in einem zurückgibt. Intuitiv wird man, ohne den Konstruktor zu kennen, vermuten, dass dim3 mit der Dimension bzw. Größe der Pixmap erstellt wird, daher ist es durchaus zumutbar, nur das Pixmapobjekt anzugeben, wenn die Pixmap keine size()-Methode oder etwas ähnlich passendes zur Verfügung stellt.

dimension< std::size_t > dim1(size());   // OK
dimension< std::size_t > dim2(rect());   // OK
dimension< std::size_t > dim3(pixmap()); // Grenzwertig

// OK, aber warum erst height, dann width?
dimension< std::size_t > dim4(pixmap().height(), pixmap().width());

Natürlich könnte man, wie bei dim4, auch explizit die beiden Parameter angeben, aber wie im Kommentar schon angedeutet, werden sich hier viele Programmierer einen Augenblick lang fragen, warum erst die Höhe und dann die Breite angegeben wird. In den allermeisten Fällen, in denen man von Breite und Höhe spricht, ist es nun mal genau umgekehrt. Bei Matrizen spricht man immer von Zeilen und Spalten und zwar in dieser Reihenfolge. Das äquivalent zu einer Anzahl von Zeilen ist aber nun mal die Höhe und eine Anzahl von Spalten entspricht einer Breite. Dieses kurze Nachdenken sollte man einem Leser von Nutzercode ebenfalls ersparen, denn es lenkt ihn nur unnötig vom verstehen des eigentlichen Codes ab. Daher ist der als grenzwertig markierten Variante bei dim3 gegenüber diesem Vorgehen doch der Vorzug zu gewähren. Durch die Verwendung eines im Kontext geeigneten Variablennamens, kann auch dieser Aufruf für spätere Leser intuitiv gestaltet werden. Auf die Wahl eines solchen Variablennamens haben wir jedoch leider keinen Einfluss. Das liegt einzig in der Hand des zuständigen Programmierers.

Es gibt noch ein weiteres, sehr starkes Argument dafür, den Konstruktor als explicit zu deklarieren. Nehmen Sie an, sie besäßen eine Funktion, die als Parameter eine Dimension erwartet. Wäre eine implizite Typumwandlung mit diesem Konstruktor möglich, könnten hier beliebige Objekte mit einer kompatiblen width()- und height()-Methode übergeben werden. Ist der Konstruktor explizit, muss immer eine Umwandlung mittels static_cast oder, falls das als intuitiv empfunden wird, durch explizite Erzeugung eines temporären Objekts erfolgen.

Wie Sie bereits bemerkt haben werden, machen wir uns viele Gedanken darüber, wie eine Klasse so gestaltet werden kann, dass ein Nutzer leicht Code schreiben kann, den später wiederum ein Leser seines Codes, leicht versteht. Unsere Entscheidungen haben also nicht nur wesentlichen Einfluss auf den Nutzer unserer Klasse, sondern auch noch auf den Nutzer von dessen Code. Wenn wir bei unserem Klassendesign gute Arbeit leisten, legen wir den Grundstein für Code, der leichter zu warten ist. Wenn wir dagegen schlechte Entscheidungen treffen, haben auch Nutzer unserer Klasse kaum eine Chance ihren Code intuitiv zu gestalten. Die Aufgabe, die uns hier zu Teil wird, ist also ein ausgesprochen verantwortungsvolle. Umsomehr, wenn Sie daran denken, dass die Schnittstellen unserer Klassen später nicht geändert werden können, ohne dass Benutzercode dadurch inkompatibel wird.

Elemente vertauschen

Das Funktionstemplate swap() vertauscht zwei Elemente gleichen Typs. Falls für einen Datentyp keine eigene swap()-Funktion deklariert ist, wird auf die Standardfunktion std::swap() zurückgegriffen. Diese wird Objekt Zwei kopieren, anschließend Objekt Eins an Objekt Zwei zuweisen und schließlich das kopierte Objekt, an Objekt Eins zuweisen. Objekte die std::swap() vertauschen kann, müssen also kopierkonstruierbar und kopierzuweisbar sein. Dieses Vorgehen ist für viele Objekte zu Zeitaufwendig und außerdem fängt man sich durch den potentiellen Aufruf eines Kopierkonstruktors und einer Kopierzuweisung die Gefahr ein, dass innerhalb der swap()-Funktion unnötig Ausnahmen geworfen werden könnten. Entsprechend bietet es sich an, für eigene Datentypen auch eine eigene swap()-Funktion anzubieten, welche die spezifischen Eigenschaften des eigenen Datentyps ausnutzt.

Nun ist es so, dass Funktionstemplates ausschließlich total spezialisiert werden können. Das heißt, Sie müssen den konkreten Typ kennen, den die übergeben Objekte haben. Eine Spezialisierung für alle Objekte vom Typ einer dimension< T >, wobei T ein beliebiger Typ ist, lässt sich also nicht durchführen. C++ erlaubt für Funktionstemplates stattdessen die Möglichkeit der Überladung, was fast den gleichen Effekt hat. Das große Problem besteht darin, dass eine Überladung zum Erstellen einer neuen swap()-Funktion führt. Also einer, die nicht zur Menge, der durch das ursprüngliche Template generierten Funktionen gehört. Dass Hinzufügen von etwas neuem zum Namensraum std ist jedoch laut C++-Standard nicht gestatten. Sie handeln sich undefiniertes Verhalten ein, wenn Sie so etwas versuchen.

Die Lösung besteht darin, nicht explizit die std-Version von swap() aufzurufen. Machen Sie std::swap() mittels using-Deklaration verfügbar und rufen Sie anschließend swap() ohne explizite Bereichsangabe auf. Ihr Compiler wird dann zunächst in dem Namensraum, in dem die Typen der Parameter definiert sind, nach einer swap()-Funktion suchen. Nur wenn dort keine gefunden wird, greift der Compiler auf die std-Version zurück. Dieses Vorgehen empfiehlt sich ohnehin für die meisten Funktionen aus std. Stellen Sie sich vor, Sie möchten für ein Objekt, eines unbekannten Datentyps T, die Quadratwurzel ziehen. Der Aufruf von std::sqrt() funktioniert nur für eingebaute Datentypen und solche, die implizit in diese umgewandelt werden können. Auch hier wäre es möglich, dass im Namensraum von T eine sqrt()-Funktion deklariert ist, die ihr Compiler nicht berücksichtigt, wenn Sie explizit nach der std-Version verlangen. Das Schöne an dieser using-Technik ist, dass sich fast nie Nachteile, aber oft Vorteile aus ihrer Nutzung ergeben.

Nun steht für uns natürlich die Frage im Raum, ob sich für unser Klassentemplate dimension spezifischen Eigenschaften erkennen lassen, die innerhalb einer swap()-Funktion zu irgendwelchen Vorteilen führen könnten. Auf den ersten Blick lautet die Antwort Nein, doch wenn man genauer hinschaut erkennt man, dass die Antwort vom konkreten Typ von T abhängt. Falls für T eine eigene swap()-Funktion deklariert ist, ist davon auszugehen, dass deren Nutzung, gegenüber der Variante mit Kopieren und Zuweisen, Vorteile bringen würde. Diese potentiellen Vorteile könnten wir nutzen, indem wir in einer eigenen spezifischen swap()-Funktion, für beide Membervariablen swap() aufrufen. Dabei müssen wir selbstverständlich die oben genannt using-Technik verwenden, um auf std::swap() zurückzugreifen, falls es keine spezifische Version für T gibt. Um auf die privaten Member der Klasse zugreifen zu können, muss die swap()-Funktion natürlich ein Member oder Freund der Klasse sein. Üblicherweise wird eine Memberfunktion swap() deklariert, welche die eigentliche Arbeit ausführt und eine nicht befreundete Nichtmemberfunktion, welche die Memberfunktion aufruft und natürlich vom Compiler gefunden wird, wenn swap() in Zusammenhang mit Objekten der Klasse dimension aufgerufen wird. In der C++-Standardbibliothek wird dies übrigens genau so gemacht. Sie können sich ja mal beispielhaft den Container std::vector ansehen. Auch dort gibt es eine Memberfunktion swap(), welche die eigentliche Arbeit erledigt. Unserer Implementierung sieht folgendermaßen aus:

template < typename T >
class dimension{
public: // ...
    void swap(dimension& rhs){
        using std::swap; // Falls keine spezielle swap verfügbar
        swap(rows_, rhs.rows_);
        swap(columns_, rhs.columns_);
    }
// ...
};

template < typename T >
inline void swap(dimension< T >& lhs, dimension< T >& rhs){
    lhs.swap(rhs);
}

Realistisch betrachtet, wird T für unseren dimension-Typ wohl in den aller meisten Fällen ein eingebauter Datentyp sein. Für solche wäre die Optimierung unnötig. Die Frage ist nun, ob sich aus unserem Vorgehen, für alle Memberdaten swap() aufzurufen, irgendwelche Nachteile ergeben können. Offensichtlich ist natürlich, dass es Nachteile bei der Wartung des Codes mit sich bringt. Falls ein Datenmember zur Klasse hinzugefügt wird, muss auch unsere swap()-Funktion erweitert werden. Noch schlimmer Folgen dieser Art hätten wir zu befürchten, wenn die Klasse Teil einer Vererbungshierarchie wäre, denn dann müssten auch Datenmember der Basisklasse beachtet werden. Kompensieren ließe sich dies ein wenig, indem eine swap()-Methode neben dem Tauschen der eigenen Datenmember, immer auch ein swap() für den Basisklassenanteil aufruft. Das ist ohnehin sinnvoll, denn auf eventuelle private Datenmember der Basisklasse, hat die swap()-Methode ja gar keinen Zugriff. Dies ist hier zwar nicht gegeben, sollte aber immer mit bedacht werden, denn auch solche Hierarchien können sich im Laufe der Zeit ändern.

Wir sollten uns noch einmal genauer anschauen, was die std::swap()-Funktion in unserem konkreten Beispiel bewirken würde und was genau unsere swap()-Methode im Unterschied dazu tut, wenn für T keine spezielle swap()-Funktion existiert. Für die folgende Betrachtung werden die Begriffe Kopierkonstruktor und Kopierzuweisung auch genutzt, wenn es sich um eingebaute Datentypen handelt. In diesem Fall wird statt einen Funktionsaufruf durchzuführen, natürlich einfach eine binäre Kopie erstellt.

Die std::swap()-Funktion ruft zunächst den Kopierkonstruktor von dimension< T > auf. Dieser ruft dann zweimal den Kopierkonstruktor von T auf, wobei natürlich von T abhängt was dieser tut. Als nächstes wird die Kopierzuweisung von dimension< T > aufgerufen und diese ruft wiederum zwei mal die Kopierzuweisung von T auf. Es folgt wiederum eine Kopierzuweisung von dimension< T >, mit den eben beschriebenen Folgen.

Unsere swap()-Methode ruft zweimal infolge std::swap() mit T-Objekten als Parameter auf. Beide male werden zunächst der Kopierkonstruktor von T und anschließend zweimal die Kopierzuweisung von T aufgerufen. Wie sie sehen, unterscheiden sich die beiden Varianten im Wesentlichen, lediglich in der Reihenfolge, in der die Funktionen aufgerufen werden.

Nehmen wir noch einmal an, T wäre ein eingebauter Datentyp, was wir ja als wahrscheinlich erachten. dimension< T > verwendet die compilergenerierten Versionen für Kopierkonstruktor und Kopierzuweisung, daher haben wir keine wirkliche Sicherheit, wie der Compiler diese Implementiert. Falls T ein eingebauter Datentyp ist, wäre es durchaus legitim, wenn der Compiler statt einer binären Kopie der einzelnen Memberdaten, einfach eine binäre Kopie des gesamten Objekts erstellt. Dies kann unter Umständen zu einer Verbesserung der Performance beitragen. Genau diese potentielle Optimierung erschweren wir dem Compiler, wenn wir eine eigene swap()-Funktion in der oben gezeigten Art implementieren.

Aufgrund dieser Abwägungen entscheiden wir uns dagegen, eine eigene swap()-Funktion für dimension< T > zu implementieren. Im Folgenden sind die entscheiden Gegenargumente noch einmal kurz zusammengefasst:

• Die Wartbarkeit des Codes wird erschwert.
• Vorteile der eigenen Implementierung sind nur zu erwarten, wenn es sich bei T nicht um einen eingebauten Datentyp handelt. Für T müsste eine spezielle swap()-Funktion existieren. Dies halten wir für sehr unwahrscheinlich.
• Es sind eventuell Laufzeitnachteile zu erwarten, falls T ein eingebauter Datentyp ist. Dies halten wir für den häufigsten Fall.

Vergleichsoperatoren

Als Vergleichsoperatoren kommen natürlich nur Gleichheit und Ungleichheit in Frage, da sich die übrigen 4 Operatoren nicht sinnvoll definieren lassen. Wir werden nachfolgend sehr ausführlich betrachten, welche Möglichkeiten für die Implementierung in Frage kommen würden. Dabei gehen wir insbesondere auf eine Technik ein, die in Zusammenhang mit Templates oft nützlich ist. Wir werden jedoch auch zu dem Schluss kommen, dass es an dieser Stelle, ähnlich der swap()-Funktion, mehr Überlegungen gibt, die gegen die Verwendung dieser Technik, an dieser Stelle, sprechen. Die Argumentation für eine Verwendung mag entsprechend etwas konstruiert wirken. Dennoch gibt sie sehr gut die Anwendungsmöglichkeiten wieder und wir werden diese Technik später noch intensiv einsetzen.

Die Frage, vor der wir im Moment stehen, ist, auf welche Weise wir die Vergleichsoperatoren implementieren sollten. Wir könnten sie zu Membern machen oder sie als friend deklarieren. Wir können sie auch als gewöhnliche Funktion deklarieren, etwas komplizierter ausgedrückt: als Nicht-befreundete-Nichtelementfunktionen. Gewöhnliche Funktionen ist an dieser Stelle natürlich auch etwas untertrieben, denn natürlich müssten sie in jedem Fall als Funktionstemplates implementiert werden. Um den Text nicht unnötig in die Länge zu ziehen, verzichten wir jedoch darauf, im Folgenden jedes mal explizit darauf hinzuweisen, dass es sich um ein Funktionstemplate handelt, wenn dieses offensichtlich ist. Weiterhin werden wir nur den Gleichheitsoperator betrachten, für den Ungleichheitsoperator gilt aber alles äquivalent.

Nun, was müssen wir bei der Deklaration also beachten? Die beiden Parameter der Funktion sind gleichwertig. Es ist also egal, ob Sie nun a == b oder b == a schreiben und entsprechend sollte es auch immer möglich sein, die beiden Parameter gegeneinander zu vertauschen, ohne dass sich der Compiler darüber beschwert. Solange a und b vom gleichen Typ sind, ist das der Fall. Was passiert jedoch, wenn b von einem Typ ist, der implizit in ein dimension-Objekt gewandelt werden kann? In diesem Fall wäre eine implizite Typumwandlung nötig. Falls der Operator als Member deklariert ist, so ist diese implizite Typumwandlung ausschließlich für den zweiten Parameter möglich, der erste Parameter, also this, muss immer explizit vom Typ der Klasse sein, zu welcher der Member gehört. Folglich ist eine Deklaration als Member, für die Gleichheitsoperatoren generell ungeeignet. Wir nehmen nachfolgend an, der Operator wäre wie folgt als gewöhnliche Funktion deklariert:

template < typename T >
bool operator==(dimension< T > const& lhs, dimension< T > const& rhs){
    return lhs.rows() == rhs.rows() && lhs.columns() == rhs.columns();
}

Besäße dimension einen nicht-expliziten Konstruktor, welcher die Umwandlung verschiedener Objekte nach dimension ermöglicht, so wäre dies bereits ein starkes Argument dafür, eine implizite Umwandlung, für die Parameter unseres Vergleichsoperators, zu unterstützen. Da dies nicht der Fall ist, müssen wir uns mit einem Notkonstrukt behelfen, das kaum praktische Relevanz haben dürfte, um eine Technik zu betrachten, die genau diese implizite Umwandlung erlaubt. Nehmen Sie an, Sie besäßen einen Typ size, welcher, äquivalent zu dimension, eine Breite und Höhe speichert. Es kann sinnvoll sein, wenn Objekte dieser beiden Typen direkt gegeneinander verglichen werden können. Sofern Sie einen Castoperator (unser Notkonstrukt) für die Umwandlung nach dimension besitzen, wird der Compiler beim Aufruf des Gleichheitsoperator, eine implizite Umwandlung für Ihren Typ size nach dimension ausführen. Praktisch könnte das etwa so aussehen:

// Typ size (kurz und unschön um Platz zu sparen)
struct size{
    std::size_t width, height;

    // Castoperator in eine dimension< std::size_t >
    operator mitrax::dimension< std::size_t >()const{
        return mitrax::dimension< std::size_t >(width, height);
    }
};

int main(){
    size                             size_1 = {5, 5};
    mitrax::dimension< std::size_t > size_2(5, 5);

    std::cout << (size_1 == size_2) << std::endl;
}

---

Funktioniert mit der aktuellen Deklaration des Gleichheitsoperators nicht…

Da der Vergleichsoperator eine Nicht-befreundete-Nichtelementfunktionen ist, wird der Compiler die Funktion erst instantiieren, wenn sie zum Ersten mal aufgerufen wird. Da der Compiler, an dieser Stelle, nach einer Funktion mit den Parametertypen size und dimension< std::size_t > sucht, wird er ein Funktionstemplate, das mit 2 Parametern gleichen Typs aufgerufen wird, nicht in Betracht ziehen. Dies ist auch sinnvoll, denn eine Instantiierung von Templates, in der Hoffnung dabei eine Variante zu finden, die nach impliziten Typumwandlungen aufgerufen werden kann, ist nicht nur sehr aufwendig, sondern meist auch unmöglich. Sobald für beide Parametertypen ein Operator, mit 2 typgleichen Parametern existiert, was fast immer der Fall ist, entsteht eine Mehrdeutigkeit, die der Compiler nicht auflösen kann.

Wir müssen uns also die Frage stellen, wie wir den Compiler dazu bringen, den Gleichheitsoperator gemeinsam mit der Klasse dimension< std::size_t > zu instantiieren. Dies ist auf jeden Fall für Memberfunktionen der Fall. Wir haben jedoch schon festgestellt, dass dies nicht in Frage kommt. Es ist in der Tat möglich, eine Nicht-Elementfunktion innerhalb einer Klasse zu definieren. Um dem Compiler mitzuteilen, dass es sich nicht um eine Elementfunktion handeln soll, machen wir die Funktion zu einem friend der Klasse. Wenn dies geschieht, wird der Compiler die Funktion gemeinsam mit der Klasse instantiieren. Etwas exakter: Er wird die Funktion, welche eventuell von den Templateparametern der Klasse abhängt, überladen. Es handelt sich hier also nicht um ein Funktionstemplate, sondern um eine Reihe unabhängiger Funktionen gleichen Namens. Betrachten wir einige Beispiele, um uns klar zu machen, was dies bedeutet.

#include <iostream>
#include <iomanip>  // Für setw
#include <typeinfo> // Für typeid-struct

template < typename T > struct A;

struct B{}; // Deklaration von 2 Klassen
struct C{}; // zur Instantiierung von A

// Funktionstemplate test
template < typename T >
void test(T const&){
    std::cout << std::setw(15) << "test< T >(T): " << typeid(T()).name() << std::endl;
}

// Überladung von test() für ein Objekt des Typs A< C >
void test(C const&){
    std::cout << std::setw(15) << "test(C): " << typeid(C()).name() << std::endl;
}

// Funktionstemplate test() für alle Instantzen von A< T >
template < typename T >
void test(A< T > const&){
    std::cout << std::setw(15) << "test< A< T > >(A< T >): " << typeid(T()).name() << std::endl;
}

template < typename T >
struct A{
    // Überladung von test() für jedes Instantiierte A< T >
    friend void test(A const&){
        std::cout << std::setw(15) << "test(A< T >): " << typeid(A()).name() << std::endl;
    }
};

int main(){
    std::cout << std::setw(25) << "test(A< B >()):"; test(A< B >());
    std::cout << std::setw(25) << "test(A< C >()):"; test(A< C >());
    std::cout << std::setw(25) << "test< A< B > >(A< B >()):"; test< A< B > >(A< B >());
    std::cout << std::setw(25) << "test< A< C > >(A< C >()):"; test< A< C > >(A< C >());
    std::cout << std::setw(25) << "test(B()):"; test(B());
    std::cout << std::setw(25) << "test(C()):"; test(C());
    std::cout << std::setw(25) << "test< B >(B()):"; test< B >(B());
    std::cout << std::setw(25) << "test< C >(C()):"; test< C >(C());
}

Ausgabe:

.         test(A< B >()): test(A< T >): F1AI1BEvE
          test(A< C >()): test(A< T >): F1AI1CEvE
test< A< B > >(A< B >()): test< T >(T): F1AI1BEvE
test< A< C > >(A< C >()): test< T >(T): F1AI1CEvE
               test(B()): test< T >(T): F1BvE
               test(C()):      test(C): F1CvE
          test< B >(B()): test< T >(T): F1BvE
          test< C >(C()): test< T >(T): F1CvE

---

Bemerkung: Die Ausgabe der Methode name() kann bei Ihnen anders sein.

Wenn der Compiler die richtige Überladung für einen Funktionsaufruf herausfinden soll, wählt er jene, die am besten zum übergebenem Parameter passt. Wird etwa ein Objekt vom Typ A< C > übergeben, so passt das Template, das ein Objekt vom Typ A< T > übernimmt besser zu dem Aufruf, als das Template das ein Objekt vom Typ T übernimmt. Noch besser passt allerdings die Überladung, die ein Objekt vom Typ A< C > übernimmt. Sie sehen keine solche Überladung? Nun, durch die Instantiierung von A mit C wurde die friend-Funktion innerhalb der Klasse zu genau dieser Überladung. Entsprechend stammt die Ausgabe in Zeile zwei aus dieser Funktion. Verlangt man hingegen explizit nach einer Instanz eines Funktionstemplates, wie in Zeile 4 der Ausgabe, so wird die passendste Variante unter die Funktionstemplats ausgewählt.

Ein weiterer interessanter Effekt ergibt sich, wenn Sie eine friend-Funktion innerhalb einer Templateklasse definieren, deren Parameter nicht von den Templateparametern des Klassentemplats abhängen. In diesem Fall wird der Compiler bei der zweiten Instantiierung des Klassentemplats als Fehler vermelden, dass diese Funktion zuvor bereits definiert wurde. Wie bereits gesagt, nimmt der Compiler eine Überladung der Funktion vor und diese ist nur möglich, wenn sich die Parameter auch unterscheiden.

Eine weitere, wesentlich wichtigere Folge ist jedoch, dass Sie die befreundete Funktion, sofern sie von den Templateparametern des Klassentemplats abhängt, nicht außerhalb der Klasse definieren können. Im Gegensatz zu Memberfunktion, hängt eine befreundete Funktion schließlich nicht direkt von dem Klassentemplate ab. Da es sich bei der Funktion nicht um ein Template, sondern um eine Reihe von gewöhnlichen Überladungen handelt, müssten Sie bei jeder neuen Instantiierung auch manuell eine neue Definition für den betreffenden Typ schreiben. Das funktioniert syntaktisch, ergibt aber überhaupt keinen Sinn. Ihr Ziel ist es ja, für jede beliebige Instantiierung automatisch eine passende Funktion zu haben. Dass die Funktion innerhalb der Klasse definiert werden muss, hat wiederum zur Folge, dass eine solche Funktion implizit inline ist. Falls dies für Sie aus irgendeinem Grund ein Problem sein sollte, dann lassen Sie die befreundete Funktion, welche innerhalb der Klasse definiert ist, einfach eine Instanz eines Funktionstemplates aufrufen, dass außerhalb definiert ist und die eigentliche Arbeit verrichtet.

Ihnen wird zweifellos aufgefallen sein, dass wir das Schlüsselwort friend hier auf eine Weise missbrauchen, die unseren Wunsch nach einer, von der Klassentemplate-Instanzen abhängigen, Funktionsinstantiierung erfüllt. friend ist eigentlich dafür gedacht, einer Nicht-Memberfunktion Zugriff auf geschützte und private Member der Klasse zu gewähren. Dies stellt sich bei unserer Technik als unerwünschter Seiteneffekt dar. Es gibt keinen Grund, warum der Vergleichsoperator Zugriff auf diese Member haben sollte, da er durch die Zugriffsmethoden auch ganz bequem lesend auf die Daten zugreifen kann. Wie also vermeiden wir, dass die Deklaration als friend eine derartigen Zugriffsmöglichkeit zur Folge hat? Die Antwort lautet, wir machen uns eine andere Eigenschaft von Freundschaft zu nutze. Freundschaft wird nicht vererbt, also legen wir die Operatoren in einer Basisklasse an.

Diese Basisklasse stellt keine „ist ein“-Beziehung dar, sondern eine „ist Implementiert in Form von“-Beziehung. Solche Beziehungen sind privat, der Nutzer unserer dimension-Klasse, braucht nichts über diese Basisklasse zu wissen. Das nächste Problem das sich ergibt, besteht darin, dass in der Basisklasse natürlich noch nicht bekannt sein kann, wie die abgeleitete Klasse heißen wird. Außerdem müssen wir sicherstellen, dass die Basisklasse für jede abgeleitete konkrete Klasseninstanz eine andere ist. Hier schlagen wir zwei Fliegen mit einer Klappe. Wir machen die Basisklasse ebenfalls zu einem Template und übergeben als Templateparameter die abgeleitete Klasse. Solange wir innerhalb der Basisklassendefinition nicht ein konkretes Objekt der abgeleiteten Klasse benötigen, ist dies ohne eine vollständige Definition der abgeleiteten Klasse möglich.

Solange wir nicht versuchen, auf etwas aus der Definition der abgeleiteten Klasse, innerhalb der Basisklasse, zuzugreifen, genügt deren Deklaration. Sie können ja beispielsweise mal scherzeshalber versuchen, auf einen typedef aus der abgeleiteten Klasse zuzugreifen. Der Compiler wird dies, mit einem Verweis auf die noch nicht definierte Klasse, quittieren. Die als friend deklarierte Funktion benötigt zwar intern eine vollständige Definition der abgeleiteten Klasse, aber zu dem Zeitpunkt, da deren Funktionsrumpf instantiiert wird, ist die komplette Definition der abgeleiteten Klasse bereits bekannt. Da die Basisklasse den Nutzer nicht interessieren muss, packen wir sie außerdem in den Namensraum detail. Das Ganze sieht folgendermaßen aus:

namespace detail{ // Forward-Deklaration der Basisklasse
    template < typename Derived > struct instantiate_with_dimension;
}

// Unsere dimension-Klasse mit privater Vererbung
template < typename T >
class dimension: private detail::instantiate_with_dimension< dimension< T > >{
public:
    // ...
};

namespace detail{
    // Definition der Basisklasse
    template < typename Derived > struct instantiate_with_dimension{
        // Definition (gleichzeitig auch Deklaration) der beiden Operatoren
        friend bool operator==(Derived const& lhs, Derived const& rhs){
            return lhs.rows() == rhs.rows() && lhs.columns() == rhs.columns();
        }
        friend bool operator!=(Derived const& lhs, Derived const& rhs){
            return !(lhs == rhs);
        }
    };
}

Von dieser Konstruktion ausgehend, wollen wir betrachten, wie sich C++ aufgrund der neu gewonnenen Möglichkeiten zu impliziten Typumwandlung verhält. Würde unser Beispiel so aussehen, dass auch für die weiter oben eingeführte size-Klasse ein Gleichheitsoperator deklariert ist, wird der Compiler sich beide Versionen ansehen und feststellen, das nur die Variante mit dimension< std::size_t >-Parametern, mittels impliziter Typumwandlung, aufgerufen werden kann. Falls nun jedoch size auch über einen Konstruktor verfügt, der ein dimension< std::size_t >-Objekt übernimmt, haben wir schließlich doch ein Mehrdeutigkeit erreicht.

struct size{
    size(std::size_t w, std::size_t h):width(w),height(h){}
    size(mitrax::dimension< std::size_t > const& d):width(d.rows()),height(d.columns()){}

    std::size_t width;
    std::size_t height;

    // Castoperator in eine dimension< std::size_t >
    operator mitrax::dimension< std::size_t >()const{
        return mitrax::dimension< std::size_t >(width, height);
    }
};

bool operator==(size const& lhs, size const& rhs){
    return lhs.width == rhs.width && lhs.height == rhs.height;
}

int main(){
    size                             size_1(5, 5);
    mitrax::dimension< std::size_t > size_2(5, 5);

    // Fehler: Mehrdeutige Aufruf von operator==()
    std::cout << (size_1 == size_2) << std::endl;
}

Der Compiler könnte hier, mittels Castoperator, eine Umwandlung von size_1 nach mitrax::dimension< std::size_t > vornehmen und den Gleichheitsoperator für zwei dimension< std::size_t >-Objekte wählen oder size_2 mit Hilfe des Konstruktors in ein size-Objekt umwandeln und den Operator der zwei size-Objekte übernimmt wählen. Die Lösung des Problems ist einfach: Entfernen Sie den Castoperator. Anschließend wird der Compiler eine implizite Typumwandlung des dimension< std::size_t > nach size durchführen und den Vergleichsoperator mit den size-Parametern verwendet.

Wenn Sie es nun für wahrscheinlich halten, dass eine size-Klasse, die in Zusammenhang mit dimension< std::size_t > verwendet wird, auch einen Konstruktor besitzt, der dimension< std::size_t >-Objekt übernimmt, dann habe Sie damit vermutlich recht. Warum also die Mühe, wenn am Ende im Zweifelsfall doch der Vergleichsoperator der size-Klasse verwendet wird? Nun, möglicherweise enthält Ihre Klasse neben den Angaben über eine Höhe und eine Breite noch andere Informationen. Dann ist es viel unwahrscheinlicher, dass es einen Konstruktor gibt, der nur ein dimension< std::size_t >-Objekt übernimmt. Für eine solche Klasse kann der Castoperator nach dimension< std::size_t > durchaus sinnvoll sein. Möglicherweise ist hier jedoch auch eine explizite Typumwandlung nach dimension< std::size_t > die bessere Wahl. Das hängt davon ab, ob sich die implizite Umwandlung intuitiv nutzen lässt oder nicht. Beispielsweise ergäbe es keinen Sinn eine Matrix implizit nach dimension zu wandeln. Eine Matrix und eine 2D-Größenangabe sind nicht vergleichbar. Eine explizite Umwandlung könnte beispielsweise durch den Aufruf einer (Member-)Funktion geschehen, die ein entsprechendes dimension< std::size_t >-Objekt zurückgibt.

Ein viel wesentlicher Vorteil besteht jedoch, wenn size ebenfalls ein Template ist und seinen Vergleichsoperator als Nicht-befreundete-Nichtelementfunktion deklariert. Dann stellt der Compiler keine Mehrdeutigkeit fest, weil er sich die Template-Instantiierungen mit gleichen Parametern, aus den oben genannten Gründen, nicht ansieht.

template < typename T >
struct size{
    T width, height;

    size(T w, T h):width(w),height(h){}
    // Konstruktor mit mitrax::dimension< std::size_t >
    size(mitrax::dimension< std::size_t > const& d):width(d.rows()),height(d.columns()){}

    // Castoperator in eine dimension< std::size_t >
    operator mitrax::dimension< T >()const{
        return mitrax::dimension< T >(width, height);
    }
};

template < typename T >
bool operator==(size< T > const& lhs, size< T > const& rhs){
    return lhs.width == rhs.width && lhs.height == rhs.height;
}

int main(){
    size< std::size_t >              size_1(5, 5);
    mitrax::dimension< std::size_t > size_2(5, 5);

    std::cout << (size_1 == size_2) << std::endl; // OK
}

Wird operator==() als Member oder befreundete-Nichtelementfunktion deklariert, ist der Aufruf natürlich wieder mehrdeutig. Anzumerken ist, dass eine Implementierung als Methode, wie oben schon angemerkt, sehr schlechter Stiel wäre, da hierbei nur für den zweiten Parameter implizite Umwandlungen möglich wären. Ein solches grundlos unterschiedliches Verhalten, ist ein deutliches Zeichen für Unwissenheit, um die Feinheiten von C++. Wenn Sie so etwas sehen, dann weisen Sie den Ersteller nach Möglichkeit darauf hin und erklären Sie ihm, warum das Quatsch ist. Ein potentiell guter Programmierer wird erfreut sein, etwas dazulernen zu können.

Real bleibt also nur ein Problem, wenn size kein Template ist oder wenn size ein Template ist und der Operator mit einer ähnlichen Technik deklariert wird, wie wir es für die dimension-Operatorüberladung getan haben. In diesem Fall müssen Sie tatsächlich abwägen, welche implizite Typumwandlung sinnvoller ist. In den meisten Fällen wird die Wahl wohl auf den Konstruktor fallen, da andernfalls keine intuitive Erstellung eines size-Objekts aus einem dimension-Objekt möglich ist. Die Umwandlung nach dimension würde dann, wie oben angedeutet, als Memberfunktion, die ein dimension-Objekt zurückgibt, explizit ausgeführt werden müssen.

Wirkliche große Vorteile würde diese Technik nur bringen, wenn dimension selbst eine Reihe von Konstruktoren besäße, welche eine implizite Umwandlung nach dimension erlauben. Dies könnte zum Beispiel in Form eines nicht-expliziten Konstruktortemplats der Fall sein. Für unsere Implementierung werden wir auf die Verwendung dieser Technik verzichten, da die oben verwendete Krücke, mit dem Castoperator in size, praktisch kaum vorkommen wird. Typischerweise wollen Sie eine implizite Umwandlung für bereits existierende Klassen und denen können Sie nicht nachträglich einen Castoperator verpassen. Dennoch ist es wichtig, dass Sie diese Technik verstanden haben, denn wir werden sie in den folgenden Kapiteln in verschiedener Weise einsetzen.

Helferlein

Da es oft nötig ist, die Anzahl der Elemente bezüglich einer Dimension zu ermitteln, werden wir noch eine kleine Helferfunktion bereitstellen. Diese berechnet einfach das Produkt der Anzahl von Zeilen und Spalten einer übergebenen Dimension. Das ganze sieht folgendermaßen aus:

template < typename T >
T elements(dimension< T > const& value){
    return value.rows() * value.columns();
}

Auf die gleiche einfache Weise kann sich der Nutzer selbst Komfortfunktionen für unsere Datentypen schreiben. Aufgrund der argumentabhängigen Namenssuche muss beim Aufruf kein Namensraum angegeben werden. Wenn der Nutzer in einem eigenen Namensraum eine Komfortfunktionen verfasst, dann muss er eine using-Deklaration verwenden, um den Namen verfügbar zu machen. Das werden Sie im Kapitel über die Rechenoperatoren aber noch genauer nachlesen können.

Die Matrixklasse

Das matrix-Klassentemplate ist das Herzstück von mitrax. Alle Inhalte dieses Kapitels stehen in der Datei matrix.hpp. Wir haben bereits festgestellt, dass eine Matrix aus einer Dimension und den entsprechend angeordneten Elementen besteht. Einen Datentyp für die Dimension haben wir uns im letzten Kapitel geschaffen. Den Datentyp für die Elemente wollen wir nicht selbst vorgeben, daher ist dies ein Templateparameter. Somit bleibt noch die Frage, wie wir unsere Elemente speichern. Was wir benötigen, ist im Grunde, ein zweidimensionales Array. Da uns die Standardbibliothek keinen entsprechenden Container zur Verfügung stellt, werden wir uns selbst um die zweidimensionale Anordnung unserer Elemente kümmern müssen. Da wir einen schnellen Zugriff auf alle Elemente wünschen, werden wir einen Container wählen, der Random-Access-Iteratoren anbietet. Anhand dieser Überlegungen erscheint std::vector geeignet.

Klassendeklaration

Sie werden sich möglicherweise fragen, warum wir uns überhaupt auf einen spezifischen Container festlegen sollten. Wir könnten den Container schließlich genauso gut als Templateparameter festlegen und dem Nutzer somit die Möglichkeit, für besondere Optimierungen anbieten. Tatsächlich werden wir dies auch machen, aber es ergibt sofort ein Problem dadurch. Unsere matrix-Klasse sollte möglichst einfach zu Handhaben sein. Wenn ein Benutzer also eine Matrix aus float-Elementen wünscht, dann wird er sich in den meisten Fällen, keine Gedanken darüber machen wollen, in welchem Container die Elemente innerhalb der Matrix gespeichert sind. Wir verpassen dem zweiten Parameter daher als Standardwert einen std::vector.

template < typename Type, template< typename > class Container = std::vector >
class matrix;

Wenn Sie versuchen diese Deklaration zu machen, wird sich ihr Compiler beschweren, dass die Templateargumentliste von std::vector nicht kompatibel zur angegeben Liste ist. Dort steht, dass Container nur ein Templateargument erhalten soll, std::vector bekommt jedoch zwei Argumente. Das Erste ist natürlich der Datentyp der Elemente, als Zweites kann jedoch noch ein spezieller Allocator angegeben werden. Da dieser einen Standardwert besitzt, fällt dies normalerweise nicht auf, aber an dieser Stelle prüft C++ nicht, ob die Deklarationen, unter Berücksichtigung der Standardargumente, kompatibel sind. Wir müssten also für den Container zwei Templateargumente spezifizieren und innerhalb der Definition von matrix, manuell den Standard-Allocator angeben. Dies hat jedoch gleich zwei Nachteile. Zum einen ist matrix dadurch sofort inkompatibel zu allen Containern, die nicht als ersten Parameter den Typ für die Elemente und als Zweiten den Typ für einen Allocator übernehmen. Zum anderen können wir keinen eigenen Allocator mehr spezifizieren.

Dies schränkt die Möglichkeiten zu optimieren durch einen eigenen Container viel zu stark ein. Wir benötigen eine andere Strategie, um den Container zu spezifizieren. Eine für uns einfache Möglichkeit bestünde darin, nur den Container angeben zu lassen und den Typ der Daten dann aus diesem zu extrahieren. Typischerweise existiert innerhalb eines Container ein typedef auf den Datentyp, den die Elemente haben. Das Ganze könnte dann etwa so aussehen.

template < typename Container >
class matrix{
    // Typ von dem unsere Elemente sind
    typedef typename Container::value_type type;
};

Wir haben jedoch bereits erläutert, dass der Container in irgendeiner Weise, standardmäßig std::vector sein sollte. Bei diesem Vorgehen haben wir keine Chance dies anzugeben. Der Nutzer müsste den Container immer selbst mit angeben. Hinzu kommt natürlich noch, dass der Container-Typ einen typedef namens value_type anbieten muss. Dies ist nicht sonderlich kritisch, aber die Abhängigkeiten sollten dennoch möglichst gering gehalten werden. Glücklicherweise gibt es einen Mechanismus, der es uns erlaubt, den Datentyp der Elemente anzugeben und diesen auch gleich als Argument für einen Standardcontainer zu verwenden.

template < typename Type, typename Container = std::vector< Type > >
class matrix;

Jetzt muss der Nutzer zwar zweimal den Typ für die Elemente angeben, wenn er einen anderen Container wünscht, aber im Gegenzug kann er auch wirklich jeden beliebigen Container benutzen, der Elemente vom Typ Type speichert. Wenn der Nutzer keinen eigenen Container wünscht, muss er nur den Datentyp für die Elemente angeben. Die Nachteile halten sich also in Grenzen und treten insbesondere auch nur dann zu Tage, wenn der Nutzer ohnehin Sonderwünsche hat. Typischerweise wir er aufgrund dessen, ohnehin in die Dokumentation der matrix-Klasse schauen müssen, um dort zu erfahren, wie in Zusammenhang mit dem Containertypen optimiert werden kann. Diese Technik wird übrigens auch in der Standardbibliothek verwendet. Sehen Sie sich beispielsweise mal den Container-Adapter std::stack an.

Falls Sie sich nun Fragen, wie diese Optimierungsmöglichkeiten denn aussehen könnten, dann denken Sie noch einmal an den Allocator von std::vector zurück. Dieser ist eine solche Optimierungsmöglichkeit. Eine andere bestünde darin, einen Container zu verwenden, der spätes Kopieren unterstützt. Bei dieser Technik werden die Daten bei einer Zuweisung nicht sofort kopiert. Stattdessen, verweist jeder Container nur auf ein Datenpaket und dieses speichert, wie viele Container derzeit auf es verweisen. Solange kein Container schreibend auf die Daten zugreift, spricht nichts dagegen, wenn mehrere Container sich die gleichen Daten teilen. Eine Kopie muss erst ausgeführt werden, wenn ein Container schreiben auf Daten zugreift, die gerade von mehr als einem Container verwendet werden. Dies kann in bestimmten Anwendungsfällen zu erheblichen Beschleunigen führen.

Den Datentyp der Dimension können wir auf dimension< std::size_t > oder einen anderen unsigned int-Typen festlegen. Es würden sich keine praktisch relevanten Vorteile daraus ergeben, den Datentyp für die Anzahl der Zeilen und Spalten variablen zu gestalten. Negative Angaben sind nicht Sinnvoll und die Wahl eines kleineren unsigned-Typs ist praktisch ebenfalls irrelevant. Im Vergleich zur Größe der Elemente, fällt der hier genutzte Speicherplatz nicht ins Gewicht. Falls der Nutzer ohnehin nur mit sehr kleinen Matrizen arbeiten will, wird er sich nicht für die Verwendung vom mitrax entscheiden, sondern eine Bibliothek wählen, bei der er den Overhead für beliebig große Matrizen nicht zahlen muss.

Klassendefinition

Das Grundgerüst für unsere Implementierung sieht folgendermaßen aus:

template < typename T, typename Container = std::vector< T > >
class matrix{
public:
    // ... folgt noch
private:
    dimension_type dimension_;
    container_type data_;
};

Als Erstes wollen wir uns Gedanken darüber machen, welche Typen unsere Klasse nach außen hin anbieten sollte. Sie erkennen an der Deklaration der Datenmember bereits, dass die Typen für die Dimension und den Container mittels typedef definiert sein müssen. Weiterhin benötigen wir natürlich Zugriff auf den Datentyp der Elemente. Bei dieser Gelegenheit, werden wir auch gleich, analog zu den Containerklassen, typedefs für eine Referenz und eine Referenz auf const für die Elemente einführen. Neben dem Datentyp für die Dimension, sollten wir auch den Datentyp der Dimensionselemente verfügbar machen. Dies erleichtert die Lesbarkeit. Der Container verwaltet intern ebenfalls Elemente, daher sollte er auch einen size_type anbieten. Diesen werden wir einfach von der Dimension übernehmen.

Da wir ein Iteratorinterface anbieten wollen, müssen wir die typedefs iterator und const_iterator anbieten. Zusätzlich benötigen wir einen difference_type, der die Entfernung zwischen zwei Iteratoren wiedergibt. Auch hier bedienen wir uns beim Container, denn dieser muss ebenfalls alle drei anbieten. Schließlich benötigen wir noch die Typen der Proxyklassen, die wir für den Zugriff auf Zeilen und Spalten verwenden. Natürlich ist auch hier je eine konstante und eine nicht-konstante Variante notwendig. Die Datentypen, die hinter diesen typedefs stehen werden wir später noch schreiben. Für den Moment sollten Sie annehmen, dass diese bereits existieren. Das Ganze sieht dann folgendermaßen aus:

// Daten
typedef T                                    value_type;
typedef T&                                   reference;
typedef T const&                             const_reference;
typedef Container                            container_type;

// Dimension
typedef typename Container::size_type        size_type;
typedef mitrax::dimension< size_type >       dimension_type;

// Iteratoren
typedef typename Container::iterator         iterator;
typedef typename Container::const_iterator   const_iterator;
typedef typename Container::difference_type  difference_type;

// Elementzugriff
typedef mitrax::row_proxy< matrix >          row_proxy;
typedef mitrax::row_const_proxy< matrix >    row_const_proxy;
typedef mitrax::column_proxy< matrix >       column_proxy;
typedef mitrax::column_const_proxy< matrix > column_const_proxy;

Sicher werden Sie sich fragen, warum wir für dimension und die Proxyklassen explizit den Namensraum mitrax spezifizieren. matrix steht schließlich selbst in diesem Namensraum. Die Antwort ist für die Proxys bei genauerem hinsehen sofort ersichtlich. Wir überschreiben innerhalb unserer Klasse den Namen mit einer neuen Bedeutung. So ist beispielsweise row_proxy innerhalb unserer Klasse ein typedef auf irgendetwas und folglich kann der Compiler das Klassentemplate row_proxy, welches außerhalb der Klasse matrix deklariert ist, nicht mehr finden. Daher müssen wir dem Compiler an dieser Stelle sagen, dass er im Namensraum mitrax nach dem Bezeichner row_proxy suchen soll. Wir werden in Kürze eine Funktion namens dimension einführen, womit auch dieser Bezeichner überdeckt wird.

Konstruktoren

Wir werden mehrere Konstruktoren anlegen. Als Erstes natürlich einen Standardkonstruktor, der eine Matrix mit null Zeilen und Spalten definiert. Dann einen Konstruktor, der eine Matrix durch Angabe einer Dimension erstellt und dabei alle Elemente standardkonstruiert. Sinnvollerweise werden wir diese Variante als Spezialfall (Standardparameter) eines Konstruktors implementieren, der alle Elemente mit einem vorgegeben Wert belegt. Letztlich brauchen wir noch einen Konstruktor, der eine schnelle Initialisierung bei gegebenen Elementen gewährleistet. Die beiden Konstruktoren, die eine Dimension übernehmen, werden wir jeweils in zwei Ausführungen implementieren. Die Erste bekommt ein dimension-Objekt und die Zweite bekommt Zeilen und Spalten getrennt. Dies ist lediglich eine Vereinfachung für den Benutzer, da beide Varianten häufig genutzt werden.

Für die effiziente Elementinitialisierung machen wir uns die swap()-Funktion zu nutzte. Ein Container besitzt intern immer einen Zeiger auf seine Daten und entsprechend ist die swap-Funktion für gewöhnlich so überladen, dass nur die internen Zeiger ausgetauscht werden müssen. Der Nutzer kann also einen eigenen Container mit den gewünschten Daten füllen und anschließend sein Containerobjekt gegen das leere Objekt in der Matrixklasse austauschen. Dies bringt natürlich den Nachteil mit sich, dass der Nutzer für die Belegung seines Containers, die zweidimensionale Position selbst berechnen muss. Wir werden später eine Hilfsklasse konstruieren, die dieses Problem ein wenig kompensiert. Falls die Größe des übergebenen Containers nicht zur Dimension passt, werden wir eine Ausnahme werfen. Die Unannehmlichkeiten, die anschließend noch für den Nutzer verbleiben, sind der Preis, den er zahlen muss, wenn er eine effiziente Vorbelegung seiner Elemente wünscht.

Gewöhnlich würden wir die Definition nicht innerhalb der Klasse vornehmen, aber um etwas Platz zu sparen, werden wir dies innerhalb der Kapitel tun. In der Quelltextübersicht, am Ende dieses Abschnitts, finden Sie Deklaration und Definition getrennt. Unserer Konstruktoren sehen somit folgendermaßen aus:

public:
    matrix(){}

    matrix(dimension_type const& size, const_reference fill = value_type()):
        dimension_(size),
        data_(elements(), fill)
        {}

    matrix(size_type const& rows, size_type const& columns, const_reference fill = value_type()):
        dimension_(dimension_type(rows, columns)),
        data_(elements(), fill)
        {}

    matrix(dimension_type const& size, container_type& data):
        dimension_(size)
    {
        raw_data_swap(dimension_, data);
    }

    matrix(size_type const& rows, size_type const& columns, container_type& data):
        dimension_(dimension_type(rows, columns))
    {
        raw_data_swap(dimension_, data);
    }

private:
    void raw_data_swap(dimension_type const& size, container_type& data){
        if(elements(size) != data.size()){
            throw error::data_size("mitrax::matrix<>::raw_data_swap", size, data);
        }
        using std::swap;
        swap(data_, data);
    }

Wie Sie sehen, wurde das Austauschen der Container in eine private Methode ausgelagert. Da wir dies sowieso im Funktionsrumpf erledigen, haben wir keine Laufzeiteinbußen und wir werden diese Funktion später noch einmal an anderer Stelle verwenden. Den Datentyp error::data_size werden wir später im Kapitel über Ausnahmebehandlung einführen. Falls Sie das Ganze schon mal testen möchten, können Sie auch einfach einen std::logic_error werfen.

Der Standardkonstruktor setzt voraus, dass der Container standardkonstruierbar ist. Die nachfolgenden beiden Konstruktoren verlangen, dass der Container über einen Konstruktor verfügt, der eine Größe und ein Füllelement übernimmt. Die letzten beiden Konstruktoren erwarten, dass für den Container die swap()-Funktion überladen ist oder dass der Container standardkonstruierbar und kopierzuweisbar ist. Letzteres wird benötigt, falls wider Erwarten auf std::swap() zurückgegriffen werden muss. In diesem Fall sind die Konstruktoren jedoch sehr wahrscheinlich ineffizient.

Iteratorinterface

Das Iteratorinterface der Matrixklasse macht uns nur sehr wenig Mühe. Wir reichen einfach die entsprechenden Funktionen an den Container weiter. Wir bieten begin() und end() jeweils in einer konstanten und einer nicht-konstanten Variante an und zusätzlich die Funktionen cbegin() und cend(), welche äquivalent zu den konstanten Versionen sind. Diese beiden Funktionen sind auch Teil des kommenden C++-Standards. Wir werden sie jedoch die aktuellen Container-Methoden begin() und end() aufrufen lassen, was mit dem jetzigen und dem kommenden Standard kompatibel ist. Im Gegensatz zu den Standard-Iteratorfunktionen werden unsere Funktionen alle samt konstante Objekte zurückgeben. Leider ist dies bei den Standardfunktionen nicht so, weshalb man beispielsweise begin()++ schreiben kann, was, wenn Sie kurz darüber nachdenken, vollkommen sinnfrei ist. Unser Iteratorinterface sieht somit so aus:

public:
    iterator const       begin()       { return data_.begin(); }
    const_iterator const begin()const  { return data_.begin(); }
    iterator const       end()         { return data_.end(); }
    const_iterator const end()const    { return data_.end(); }
    const_iterator const cbegin()const { return begin(); }
    const_iterator const cend()const   { return end(); }

Kapazität

Unter dieser Überschrift wollen wir die Methoden zum Abfragen der Dimension einführen. Die Methode dimension() soll uns das Dimensionsobjekt liefern, zusätzlich werden wir aber noch die Methoden rows() und columns() anlegen. In der Praxis kommt es in etwa gleich häufig vor, dass die komplette Dimension benötigt wird und dass nur ein Teil der Dimension benötigt wird. Keine der beiden Varianten lässt sich effizient durch die jeweils andere ersetzen, daher bieten wir beide an. Außerdem erhöhen wir die Lesbarkeit von Clientcode, indem wir erlauben, ihn kürzer zu fassen, ohne dass dabei Information für den Leser verloren geht. Sie können ja mal versuchen, nur mit der dimension()-Methode oder nur mit den Methoden rows() und columns(), Code zu schreiben, in dem die jeweils andere Schnittstelle der matrix-Klasse günstiger wäre. Die Methoden sehen folgendermaßen aus:

public:
    dimension_type const dimension()const { return dimension_; }
    size_type const      rows()const      { return dimension_.rows(); }
    size_type const      columns()const   { return dimension_.columns(); }

Dimension ändern

Es gibt eine reichliche Menge an Situationen, in denen es sinnvoll ist, die Größe einer Matrix im Nachhinein zu verändern. Dabei muss man zwei Fälle unterscheiden. Im Ersten werden die Elemente der Matrix komplett verworfen und neu initialisiert. Im zweiten Fall wird nur die Dimension geändert, die Elemente, die auch mit der neuen Dimension noch existieren, bleiben erhalten. Betrachten wir beide Fälle etwas genauer.

Fall Eins lässt sich noch einmal nach der Art der Neuinitialisierung der Elemente aufteilen. Wie schon bei den Konstruktoren, kann auch hier wieder ein Element als Vorlage für alle anderen übergeben werden, oder es kann ein Container mit passender Größe, gegen den aktuellen Elemente-Container ausgetauscht werden. Diese zweite Variante werden wir in einer Methode namens reinit() implementieren. Sie besitzt die gleichen Nachteile wie der entsprechende Konstruktor, bietet aber auch die gleiche, sehr hohe, Effizienz.

Wenn die Elemente an ihren Positionen erhalten bleiben sollen, stellt sich natürlich die Frage, was zu tun ist, wenn die neue Matrix Elemente enthält, die in der alten nicht vorhanden waren. Wir werden das Problem dahingehend lösen, dass wir entsprechende Elemente mit einem übergeben Element auffüllen. Dieses Übergebene Element soll selbstverständlich als Standardparameter das standardkonstruierte Element verwenden, so dass der Benutzer nicht zwingend etwas angeben muss. Speziell wenn er weiß, das er die Matrix verkleinert, wäre es ziemlich nervig, einen Parameter angeben zu müssen, der niemals genutzt wird. Somit wird dies der letzte Parameter unserer resize()-Methode. Die Entscheidung bestehende Elemente zu erhalten, werden wir Standardmäßig auf true setzen. Wenn der Nutzer dies nicht wünscht, muss er es explizit abschalten, andernfalls braucht er sich keine Gedanken darüber zu machen. Unsere Implementierung sieht so aus:

public:
    void resize(dimension_type const& size,
        bool preserve = true, const_reference fill = value_type()
    ){
        container_type init(elements(size), fill); // Neuer Container

        if(preserve){
            // Länge der pro Zeile zu kopierenden Elemente ermitteln
            size_type min_columns = std::min(size.columns(), dimension_.columns());
            // Differenz von kurzen und langen Zeilen
            size_type dif_columns = std::max(size.columns(), dimension_.columns()) - min_columns;
            // Iteratoren beider Container
            iterator  data_iter = data_.begin();
            iterator  init_iter = init.begin();
            // Iterator mit den längeren Zeilen ermitteln
            iterator& bigger    = size.columns() < dimension_.columns() ? data_iter : init_iter;
            // Zeilenweise durchlaufen
            for(size_type i = size_type(); i < size.rows() && i < dimension_.rows(); ++i){
                // Iteratoren hinter das Ende des zu kopierenden Bereiches setzen
                iterator begin_data_iter = data_iter;
                iterator begin_init_iter = init_iter;
                std::advance(data_iter, min_columns);
                std::advance(init_iter, min_columns);
                // Kopie durchführen
                std::copy(begin_data_iter, data_iter, begin_init_iter);
                // Iterator mit den längeren Zeilen auf den Anfang der nächsten Zeile setzen
                std::advance(bigger, dif_columns);
            }
        }

        using std::swap;
        swap(data_, init);
        dimension_ = size;
    }

    void resize(size_type const& rows, size_type const& columns,
        bool preserve = true, const_reference fill = value_type()
    ){
        resize(matrix_size_type(rows, columns), preserve, fill);
    }


    void reinit(dimension_type const& size, container_type& data){
        raw_data_swap(size, data);
        dimension_ = size;
    }

    void reinit(size_type const& rows, size_type const& columns, container_type& data){
        reinit(matrix_size_type(rows, columns), data);
    }

Wie Sie erkennen, stellen wir auch für diese Methoden wieder je eine Version mit einem dimension-Objekt und eine mit den Einzelangaben für die Anzahl der Zeilen und Spalten bereit. Die Implementierung erfolgt natürlich nur in einer Version, da am Ende ohnehin ein dimension-Objekt benötigt wird, wird diese Version durch die andere aufgerufen. Bei der Reinitiallisierung verwenden wir wieder die Hilfsmethode raw_data_swap(), welche wir mit den Konstruktoren eingeführt haben. Da diese eine Ausnahme werfen kann, erfolgt dieser Aufruf als erstes. Somit steigt die Wahrscheinlichkeit, dass das matrix-Objekt unverändert bleibt, falls eine Ausnahme geworfen wird. Eine Garantie hierfür, kann man natürlich erst geben, wenn der Containertyp bekannt ist.

In der resize()-Methode legen wir zunächst einen neuen Container mit passender Größe an und lassen ihn mit unserem Füllelement auffüllen. Dies stellt an den Container die Anforderung, dass dieser einen entsprechenden Konstruktor anbietet. Falls preserve gesetzt ist, werden anschließend zeilenweise die Elemente aus dem alten Container kopiert, die für beide Dimensionen existieren. Die übrigen Elemente sind ja bereits auf den Füllwert gesetzt. An dieser Stelle setzten wir voraus, dass der Container Iteratoren anbietet. Da wir dies jedoch bereits in der Klassendefinition verlangt haben, muss dies immer der Fall sein. Schließlich tauschen wir den alten Container gegen den Neuen aus und weisen die neue Dimension zu.

Elementzugriff

Für den Zugriff auf Zeilen und Spalten werden wir sogenannte Proxyklassen verwenden. Der Nutzer unserer Matrixklasse muss von diesen Proxyklassen nicht unbedingt etwas mitbekommen. Was wir erreichen wollen, ist, dass der Zugriff auf ein Element innerhalb der Matrix syntaktisch mit matrix_object[3][2] oder auch mittels matrix_object.column(2).row(3) möglich ist. Dies erreichen wir, indem wir die Memberfunktion von Matrix (operator[]() bzw. column()) ein Objekt zurückgeben lassen, welches von einem Typ ist, der wiederum die zweite Memberfunktion (operator[]() bzw. row()) bereitstellt. Diesen „Zwischentyp“ bezeichnet man als Proxyklasse. Wie genau diese Proxyklasse heißt oder aussieht, ist für den Nutzer erst interessant, wenn er eine Zeile oder Spalte als Parameter an eine eigene Funktion übergeben möchte. Solange er nur auf Elemente zugreift, muss er lediglich wissen, wie der Aufruf syntaktisch aussieht.

Wir werden die Proxyklassen in einem eigenen Kapitel behandeln. An dieser Stelle werden wir einfach annehmen, sie würden bereits existieren. Unsere Zugriffsmethoden der matrix-Klasse werden also ein Objekt vom Typ einer Proxyklasse erstellen, ihm die Information mitteilen, die sie selbst erhalten haben (welche Zeile / Spalte) und das Objekt schließlich zurückgeben. Zu beachten ist, dass es für konstante und nicht-konstante Versionen der Zugriffsfunktionen getrennte Proxyklassen gibt. Dies ist äquivalent zu den Funktionen für Iteratoren, denn genau wie die Iteratoren, müssen ja auch die Proxy-Objekte wissen, ob Sie auf eine konstante oder auf eine nicht-konstante Matrix verweisen. Ob die Iteratoren bzw. Proxys selbst konstant oder nicht-konstant sind, gibt keinen Aufschluss über die Daten, auf die sie verweisen. Die zurückgegeben Objekte sind natürlich, wie schon bei den Iteratoren, wieder konstant. Somit erhalten wir folgende Zugriffsmethoden für matrix:

public:
    row_proxy const       operator[](size_type const& row_number)      { return row(row_number); }
    row_const_proxy const operator[](size_type const& row_number)const { return row(row_number); }

    row_proxy const row(size_type const& number){
        return row_proxy(*this, number);
    }

    row_const_proxy const row(size_type const& number)const{
        return row_const_proxy(*this, number);
    }

    column_proxy const column(size_type const& number){
        return column_proxy(*this, number);
    }

    column_const_proxy const column(size_type const& number)const {
        return column_const_proxy(*this, number);
    }

Modifizierer

Als Modifizierer bezeichnen wir Methoden, welche Zeilen oder Spalten (nachfolgend mit Linien abgekürzt) entfernen oder hinzufügen. Das Hinzufügen von Linien lassen wir in mitrax außen vor. Da es jedoch einige Algorithmen gibt, welche einzelne Linien löschen, werden wir diese Möglichkeit anbieten. Als Parameter bekommen unsere beiden Methoden, eine Position und die Anzahl der Linien, welche nach dieser Position gelöscht werden sollen. Das mehrere Zeilen oder Spalten gelöscht werden, kommt zwar relativ selten vor, aber wenn es doch mal nötig ist, wäre es sehr ineffizient die beiden aufeinander folgenden Linien einzeln zu löschen. Außerdem macht es uns kaum Mehrarbeit und als Standardwert werden wir für den zweiten Parameter natürlich eine Eins angeben.

Vor der eigentlichen Löschung prüfen wir, ob die entsprechenden Linien auch existieren. Falls dies nicht der Fall ist, werfen wir eine entsprechende Ausnahme. Sie können zum Testen eine std::out_of_range-Ausnahme werfen. Anschließend löschen wir die entsprechenden Elemente in unserem Daten-Container. Zum Schluss setzen wir die Dimension auf ihren neuen Wert. Das ganze sieht folgendermaßen aus:

public:
    void erase_row(size_type const& number, size_type const& count = size_type(1)){
        if(rows() > number + count){
            throw error::row_access("mitrax::matrix<>::erase_row", dimension_, rows());
        }

        // Zeilen löschen
        iterator iter = data_.begin();
        iter += number * columns();
        data_.erase(iter, iter + count * columns());
        // Dimension anpassen
        dimension_.resize(rows() - count, columns());
    }

    void erase_column(size_type const& number, size_type const& count = size_type(1)){
        if(columns() < number + count){
            throw error::column_access("mitrax::matrix<>::erase_column", dimension_, columns());
        }

        // Zeilen löschen
        for(size_type i = size_type(); i < rows(); ++i){
            iterator iter = data_.begin();
            iter += number + (columns() - count) * i;
            data_.erase(iter, iter + count);
        }
        // Dimension anpassen
        dimension_.resize(rows(), columns() - count);
    }

Wir wollen nachfolgend einige theoretische Betrachtungen zu den Anforderungen an size_type in diesen beiden Methoden vornehmen. Praktisch werden diese höchstwahrscheinlich immer erfüllt sein, den der size_type eines Container ist so gut wie immer ein ganzzahliger eingebauter Datentyp.

Falls der Standardwert für den zweiten Parameter genutzt wird, muss der Integerliteral 1 in ein size_type-Objekt konvertierbar sein. Wäre nicht explizit eine Erstellung eines size_type-Objekts angegeben, müsste diese Umwandlung zusätzlich implizit möglich sein. Die beiden Methoden verlangen, dass size_type standardkonstruierbar ist. Außerdem müssen die Operatoren operator<(), operator++(), operator+(), operator-() und operator*() für size_type überladen sein. Bei der üblichen Implementierung der letzten drei Operatoren folgt, dass size_type kopierkonstruierbar sein muss. Wegen den Vorschriften die C++ zu Random-Access-Iteratoren macht, muss size_type implizit in difference_type konvertierbar sein. Der zweite Parameter des operator+=() eines Random-Access-Iterators muss nämlich von diesem Typ sein.

swap

Wie zuvor schon erwähnt wurde, ist swap() für Container normalerweise durch eine sehr effiziente Variante überladen. Wenn Sie sich nun an unsere Überlegungen zur swap-Funktion von dimension erinnern, werden Sie dieses mal zu dem Schluss kommen, dass sich die Überladung für matrix lohnt. Wir werden einfach für alle Datenmember von matrix swap() aufrufen. Der einzige Nachteil, der sich theoretisch daraus ergibt, besteht darin, dass die swap()-Funktion ihre beiden Operanden in einem undefinierten Zustand belässt, falls bei einem der Unteraufrufe eine Ausnahme geworfen wird. Dies ist jedoch ausgesprochen unwahrscheinlich. Das swap() für die dimension-Objekte kann keine Ausnahme werfen. Dass das swap() für die Container eine Ausnahme wirft, ist ebenfalls unwahrscheinlich, denn wie bereits erläutert haben, werden hier typischerweise nur zwei Zeiger vertauscht. Da das Container-swap() noch einen Hauch kritischer ist, werden wir diesen Aufruf zuerst tätigen. Falls hier tatsächlich eine Ausnahme geworfen werden sollte, haben wir dimension noch nicht verändert und somit ist alles in Ordnung. Die Implementierung sieht wie Folgt aus:

public:
    void swap(matrix& m){
        using std::swap;
        swap(data_, m.data_);
        swap(dimension_, m.dimension_);
    }

// Außerhalb der Klasse
template < typename T, typename Container >
void swap(matrix< T, Container >& lhs, matrix< T, Container >& rhs){
    lhs.swap(rhs);
}

Helferlein

Wie bereits angedeutet, werden wir noch eine kleine Helferklasse einführen, die es den Nutzer ermöglicht, auf einfache Weise die Position in einem eindimensionalen Feld anhand einer zweidimensionalen Angabe zu berechnen. Wir erstellen zu diesem Zweck einen Funktor, also eine Klasse, die den Funktionsoperator überlädt. Im Konstruktor teilen wir dem Funktor mit, wie viele Spalten unsere Matrix letztlich haben soll. Dem Funktionsoperator übergeben wir die X- und die Y-Position. Das Ergebnis wird die eindimensionale Position innerhalb des Containers sein.

Der Datentyp der Positionen ist von der verwendeten matrix-Instanz anhängig. Da es jedoch sehr viele matrix-Instanzen gibt, die den gleichen size_type verwenden, ist es sinnvoll, wenn wir nur eine Templateinstanz unseres Funktors pro size_type anlegen. Daher werden wir die Klasse als Template mit einem Parameter anlegen. Den Zugriff auf die passende Funktorklasse realisieren wir, indem wir innerhalb unserer matrix-Klasse einen typedef für die passende Funktorklasse hinzufügen. Da der Nutzer folglich keine Kenntnis von der Definition der Funktorklasse haben muss, werden wir diese im Namensraum detail innerhalb von mitrax deklarieren.

Diesen Namensraum werden wir innerhalb des Projekts für alles verwenden, mit dem der Nutzer niemals direkten Kontakt haben sollte. Wir werden den Nutzer lediglich innerhalb der Dokumentation über die Verwendung bei indirekter Nutzung aufklären. Das hat für uns den Vorteil, dass wir uns keine größeren Gedanken über den Teil der Schnittstelle machen müssen, den der Nutzer sowieso nicht sieht. Insbesondere können wir auf diese Weise, bei einer späteren Version unserer Bibliothek, problemlos den Teil der Schnittstellen ändern, mit denen der Clientcode keinen Kontakt hat. In Zusammenhang mit den Iteratoren für die Proxyklassen werden Sie dies leicht anhand der Konstruktoren erkennen. Wir werden unsere Funktorklasse auf den Namen position_adapter taufen. Der typedef wird den gleichen Namen tragen.

namespace detail{

template < typename SizeType >
class position_adapter{
public:
    position_adapter(SizeType columns):columns_(columns){}
    position_adapter(dimension< SizeType > const& dim):columns_(dim.columns()){}

    SizeType const operator()(SizeType const& row, SizeType const& column){
        return row * columns_ + column;
    }

private:
    SizeType columns_;
};

}

template < typename T, typename Container = std::vector< T > >
class matrix{
public:
    // andere typdefs
    typedef detail::position_adapter< size_type > position_adapter;
    // ...
};

Der Nutzer kann nun zur effizienten Initialisierung einer Matrix beispielsweise folgendes schreiben, ohne sich Gedanken über die Berechnung der eindimensionalen Position machen zu müssen.

typedef mitrax::matrix< int > matrix;
matrix::dimension_type dimension(3, 5);
matrix::container_type init(elements(dimension));
matrix::position_adapter index(dimension);

for(matrix::size_type row = 0; row < dimension.rows(); ++row)
    for(matrix::size_type column = 0; column < dimension.columns(); ++column)
        init[index(row, column)] = row;

matrix a1(dimension, init);

Proxyklassen

In diesem Kapitel wollen wir dafür sorgen, dass der Zugriff auf einzelne Elemente unserer Matrix durch zweimalige Anwendung des Indexoperators erreicht werden kann. Zu diesem Zweck schreiben wir eine Reihe von Klassen, die eine Referenz auf eine Zeile oder Spalte, eines matrix-Objektes, repräsentieren. Zunächst müssen wir uns Gedanken darüber machen, welche dieser Proxyklassen wir benötigen und wie diese miteinander in Verbindung stehen. Die Inhalte dieses Kapitels stehen in der Datei proxy.hpp.

Vorüberlegungen

Einfache Vererbungshierarchie der Proxyklassen

Wie Sie bereits im vorherigen Kapitel erfahren haben, werden für konstante und nicht-konstante Zeilen- bzw. Spaltenproxys jeweils getrennte Klassen benötigt. Somit benötigen wir also vier Proxyklassen. Die Klassen für nicht-konstanten Matrizen sollten an jeder Stelle verwendet werden können, an denen ihre Äquivalente für konstanten Matrizen gefordert werden. Dies können wir scheinbar auf zweierlei Arten erreichen. Wir können die Klassen für nicht-konstanten Matrizen öffentlich von den Klassen für konstanten Matrizen ableiten, oder wir können den Klassen für konstante Matrizen jeweils einen Konstruktor verpassen, der ein Objekt aus einem Objekt der entsprechenden Proxyklasse für nicht-konstante Matrizen erstellt.

Im Prinzip würden diese vier Proxyklassen genügen, wir wollen jedoch noch etwas weiter denken. An vielen Stellen können sowohl Spalten-, als auch Zeilenproxys verwendet werden. Es ist also zu überlegen, wie wir eine solche richtungsunabhängige Verarbeitung realisieren können. Zunächst muss natürlich für beide Proxyarten eine einheitliche Schnittstelle existieren. Dann kann die gewünschte Funktion als Template erstellt werden, welches die konkrete Proxyklasse als Parameter bekommt. Diese sehr einfache Herangehensweise ist zugleich auch sehr effizient, sie weist jedoch auch ein paar Nachteile auf.

Falls innerhalb der Funktion nur wenig mit dem Proxyobjekt gearbeitet wird, entsteht eine Menge doppelter Code bei der Templateinstantiierung. Ein guter Compiler wird dies natürlich optimieren, daher wiegt diese Nachteil wahrscheinlich nicht alt so schwer. Ein anderer Nachteil besteht darin, dass der Nutzer richtungsunabhängige Funktionen immer als Templates realisieren muss. Da es nur zwei Arten von Proxys geben kann, wäre es natürlich angenehm, wenn er einfach eine allgemeine Proxyklasse als Parameter angeben könnte. Besonders problematisch wird es, wenn seine Funktion eine Proxyklasse für konstante Matrizen erwartet. Der Compiler wird, selbst bei einer Verwandtschaftsbeziehung zwischen den Proxys für konstante und nicht-konstante Matrizen, vier Instantiierungen des Funktionstemplats vornehmen, anstatt lediglich zwei für die jeweils auf konstante Matrizen bezogenen Proxyklassen.

Richtungsunabhängige Proxyklassen

Vererbungshierarchie mit richtungsunabhängigen Proxyklassen

Wir werden dieses Problem später genauer beleuchten, da zunächst klar sein muss, was die vier, zwingend benötigten, Proxyklassen anbieten müssen.

Wie Sie am Beispiel der element_swap()-Funktion noch sehen werden, sind bei der Nutzung von richtungsabhängigen Proxys leider zwei Funktionsdeklarationen notwendig, auch wenn das eigentliche Problem richtungsunabhängig ist. Es wäre natürlich praktisch, wenn wir, über eine entsprechende Vererbungshierarchie, nur noch eine Deklaration angeben müssten. Das Ganze könnte wie in der Grafik dargestellt aussehen. Dabei darf es nicht möglich sein, von den Klassen line_const_proxy und line_proxy Objekte zu erzeugten. Folglich muss line_proxy nicht von line_const_proxy abgeleitet sein, denn alle Klassen die von line_proxy abgeleitet sind, können ja zusätzlich auch indirekt von line_const_proxy abgeleitet werden.

Diese Tatsache ist insbesondere deshalb von Vorteil, weil eine zusätzliche Vererbung von line_const_proxy an line_proxy virtuell sein müsste und virtuelle Vererbung bringt immer Laufzeitnachteile mit sich. Wenn wir nun die Daten aus den richtungsunabhängigen Proxyklassen für konstante Matrizen nach line_const_proxy verschieben, funktioniert dies erst einmal sehr schön. Leider haben wir von line_proxy aus keine Möglichkeit an die Daten heranzukommen. Wir können uns eine solche Möglichkeit auf zweierlei Weise verschaffen.

Die Erste besteht darin, abstrakte virtuelle Funktionen zu verwenden, welche im privaten Bereich der richtungsabhängigen Klassen implementiert werden. Die Folge virtueller Funktionen ist jedoch unweigerlich eine wesentlich schlechtere Laufzeitperformance. Die andere Möglichkeit ist, line_proxy eben doch von line_const_proxy abzuleiten. Wenn diese Ableitung nicht virtuell geschieht, existiert die Basisklasse line_const_proxy und mit ihr auch die Datenmember, mehrfach. Wenn die Ableitung virtuell ist, ergeben sich, wie schon erwähnt, ebenfalls beträchtliche Laufzeiteinbußen und das sogar, wenn wir einen richtungsabhängigen Proxy verwenden. Daher kommt dies nicht in Frage. Wir stellen also fest, dass es keine effiziente Möglichkeit für eine derartige Implementierung gibt.

Bleibt noch die Frage zu klären, ob die Einbußen klein genug sind, um sie für eine einfachere Verwendung in Kauf nehmen zu können. Der Elementzugriff über die Proxyklassen, sollte, dank der Compileroptimierung für inline-Methoden, ebenso schnell sein, wie ein Zugriff, der direkt über eine Zugriffsmethode eines matrix-Objektes durchgeführt wurde. Wenn eine Zugriffsmethode virtuelle Funktionen aufruft, ist zumindest für diese kein inlining mehr möglich. Folglich haben wir hier eine recht drastische Einbuße, für einen schlichten Zugriff auf ein Element innerhalb eines Array. Noch schlimmer sieht die Situation aus, wenn wir mit Iteratoren arbeiten wollten, denn auch diese müssten dann in irgendeiner Form generisch sein. Wir fangen uns mindestens eine komplizierte Berechnungsmethodik ein, weil wir ja sowohl das Verhalten von Zeilen-, als auch das Verhalten von Spalteniteratoren unterstützen müssten. Außerdem währen die Iteratoren für Zeilen und Spalten zwingend vom gleichen Typ, sobald wir die richtungsunabhängige Proxyklasse verwenden. Das heißt, wir können unsinniger Weise die Vergleichsoperatoren anwenden, ohne dass der Compiler sich darüber beschwert.

Alles in allem, sind die Nachteile also überwältigend. Daher werden wir auf ein solches Konstrukt verzichten und dem Nutzer stattdessen zumuten, sich mit einer ähnlichen Technik zu behelfen, wie wir sie bei element_swap() verwenden werden. Effektiv wird er dabei glücklicherweise oft nur zwei Deklarationen schreiben müssen, denn falls er Proxys für konstante Matrizen benötigt, sind die Objekte von Proxys für nicht-konstante Matrizen kompatibel und wenn er Proxys für nicht-konstante Matrizen benötigt, können die anderen beiden Proxys ohnehin nicht verwendet werden. Nur wenn er Proxys für konstante Matrizen benötigt und die Funktion ein Template ist, kann keine implizite Typumwandlung in Proxys für nicht-konstante Matrizen stattfinden. Ein Beispiel dazu werden Sie bei der Ausgabe von Proxys sehen. Leider tritt dieser eine Fall recht häufig ein, aber eine einfacheren Weg gibt es hier nicht.

Vererbung oder implizite Typumwandlung

Wir haben oben schon angedeutet, dass es zwei Varianten gibt, um eine Kompatibilität der Proxys für nicht-konstante Matrizen, zu den Proxys für konstante Matrizen zu erzeugen. Die Erste ist eine öffentlich Ableitung, die Zweite ist ein Konstruktor innerhalb der Proxys für konstante Matrizen, der ein Objekt eines Proxys für nicht-konstante Matrizen übernimmt. Wir wollen uns die Unterschiede dieser beiden Techniken kurz ansehen, um festzustellen, welche Technik besser für unser Problem geeignet ist. Nehmen Sie an, sie besäßen die folgenden Funktionen und würden ihnen je ein Objekt vom Typ proxy übergeben.

void f1(proxy_const value);
void f2(proxy_const const& value);
void f3(proxy_const& value);

Nehmen wir zunächst an, proxy wäre öffentlich von const_proxy abgeleitet. Bei Aufruf der ersten Funktion würde unser Objekt implizit, mittels des Kopierkonstruktors von const_proxy, umgewandelt werden. Das ist für uns in Ordnung, denn innerhalb der Funktion wird ja auch nur der Basisklassenanteil benötigt. Die zweite Funktion würde das Objekt als Referenz übernehmen und uns lediglich den Zugriff auf den Basisklassenanteil gestatten. Da dieser konstant ist, haben wir keine ungewollten Änderungen zu befürchten. Ganz anders sieht es jedoch bei der Funktion f3() aus. Hier wird ebenfalls eine Referenz übernommen, jedoch lässt sich das Objekt dahinter verändern und zwar so, als wäre es tatsächlich ein proxy_const Objekt. Das bedeutet insbesondere, das wir einem solchen Objekt mittels Kopierzuweisung ein anderes Objekt vom Typ proxy_const zuweisen könnten. Wir wollen das am Beispiel der Zeilenproxys kurz ausprobieren, wobei wir allerdings auf die Nutzung einer Funktion verzichten.

matrix       dummy_matrix(2, 2); // Veränderliche Matrix (Inhalt egal)
matrix const const_matrix(2, 2); // Unveränderliche Matrix

matrix::row_const_proxy  const_proxy = const_matrix.row(0);
// Initialisierung nötig weil kein Standardkonstruktor existiert
matrix::row_proxy        dummy_proxy = dummy_matrix.row(0);

// Mit veränderlicher Matrix initialisieren
matrix::row_const_proxy& bad_proxy = dummy_proxy; 
// Gewünschten const_proxy dem Objekt hinter der Referenz zuweisen
bad_proxy = const_proxy;

// Veränderlicher Proxy bezieht sich jetzt auf eine Zeile in der konstanten Matrix
dummy_proxy[0] = 100;

Wie Sie sehen ist keinerlei const_cast notwendig, um einen Schreibzugriff auf die konstante Matrix zu bekommen. Das Ergebnis der Schreiboperation ist natürlich entweder undefiniert oder hängt zumindest von Stelle ab, an der const_matrix definiert wurde. In jedem Fall darf solcher Code nicht funktionieren, daher scheidet die öffentliche Vererbung für unsere Zwecke aus. Dieses Beispiel ist übrigens gar nicht so konstruiert, wie es auf den ersten Blick aussieht. Wenn Sie die gewünschte Zuweisung innerhalb einer Funktion ausführen, welche, wie in f3(), eine Referenz übernimmt, dann sieht es viel weniger konstruiert aus und fällt auch auf den ersten Blick viel weniger auf. So etwas kann also durchaus versehentlich geschehen.

Schauen wir uns noch an, ob bei der Verwendung einer Umwandlung mittels Konstruktor eine ähnlich böse Falle auf uns lauert. Für den Aufruf von f1() würde der Compiler wieder eine implizite Typumwandlung durchführen. Der entsprechende Konstruktor darf dabei natürlich nicht explizit sein. Auch die zweite Funktion würde eine implizite Typumwandlung nach sich ziehen. Das ist natürlich geringfügig langsamer, als bei Variante mit Vererbung, aber dagegen kann uns, mit etwas Glück, die Optimierung durch den Compiler helfen. Der Aufruf der Funktion f3() führt zu einer Fehlermeldung und das ist genau das Verhalten, das wir benötigen. Wenn eine solche Funktion aufgerufen werden soll, muss der Nutzer zuvor explizit ein Objekt vom Typ const_proxy aus seinem proxy-Objekt erzeugen und dieses übergeben.

Dieses Verhalten lässt sich übrigens auch bei Iteratoren beobachten. Es wurde ja schon mehrfach darauf hingewiesen, das Proxyklassen und Iteratorklassen sich ähnlich verhalten. In beiden Fällen repräsentieren die Objekte Daten aus einer anderen Klasse. Im Wesentlichen handelt es sich also um den gleichen Typ von Technik. Denken Sie, bei der Erstellung solcher proxyartiger Objekte, daher immer daran, dass eine öffentlich Vererbung zu unschönen Problemen führen kann. Das Mittel der Wahl heißt implizite Typumwandlung. Dass kann zwar geringfügig langsamer sein, aber dafür ist die Technik sicher und wenn ihr Compiler gut optimiert, dann ist selbst die Übergabe als Referenz auf const, genau so schnell, wie bei der Vererbung.

Proxys für konstante Matrizen

Als Templateparameter bekommen unsere Proxyklassen selbstverständlich die konkrete matrix-Klasse. Für die Namen werden wir uns, wie im Bild oben schon angedeutet, an den Konventionen für die Iteratornamen halten. Diesen stellen wir noch die Richtung, also „row“ oder „column“, voran. Somit ergeben sich die vier Namen, die im ersten Bild zur Vererbungshierarchie verwendet wurden.

Als nächstes sollten wir uns wieder fragen, welche typedefs wir benötigen. Praktischerweise sollten wir natürlich den Templateparameter wieder verfügbar machen und um den Zugriff zu erleichtern, werden wir auch den value_type von matrix wieder unter dem gleichen Namen zur Verfügung stellen. Die Elemente der Proxyklassen sind schließlich vom gleichen Typ, wie jene, der entsprechenden matrix. Da die Proxyklassen eine bestimmte Anzahl von Elemente repräsentieren, benötigen wir natürlich einen size_type. Dieser sollte ebenfalls mit jenem, aus der zugehörigen matrix-Klasseninstanz übereinstimmen.

template < typename Matrix >
class row_const_proxy{
public:
    typedef Matrix                      matrix_type;
    typedef typename Matrix::value_type value_type;
    typedef typename Matrix::size_type  size_type;

    // ...
};

template < typename Matrix >
class column_const_proxy{
public:
    typedef Matrix                      matrix_type;
    typedef typename Matrix::value_type value_type;
    typedef typename Matrix::size_type  size_type;

    // ...
};

Schließlich wurde ja bereits gesagt, dass wir auch für die Proxyklassen ein Iteratorinterface anbieten wollen. Diesmal können wir leider nicht einfach die Iteratoren eines Datenmembers durchreichen. Wir müssen die Iteratortypen selbst schreiben und da dies ein etwas aufwendigeres Unterfangen ist, werden wir das in einem eigenen Kapitel behandeln. Die drei typedefs, die wird für die Iteratoren benötigen, sind iterator, const_iterator und difference_type. Bei den Proxys für konstante Matrizen verweisen die typedefs für iterator und const_iterator sinnvoller Weise auf den gleichen Typ. Da wir jedoch an dieser Stelle nicht unkompliziert vorgreifen können, werden wir den gesamten Teil der Proxyklassen, der Iteratoren betrifft, später zusammen mit den Iteratorklassen selbst Abhandeln.

Schauen wir uns an, welche Konstruktoren wir benötigen könnten. Ein Standardkonstruktor ergibt für die Proxys keinen Sinn. Die Proxyklassen sollen ja eine Zeile oder Spalte eines matrix-Objekts repräsentieren, wie sollten wir sie also ohne ein matrix-Objekt sinnvoll Initialisieren. Einen Kopierkonstruktor könnten wir hingegen durchaus gebrauchen. Es ist gut möglich, dass ein Nutzer von mitrax, in einem Algorithmus lieber zwei Proxys vertauscht, als tatsächlich die komplette Zeile oder Spalte auszutauschen. Da für diesen Zweck üblicherweise swap() verwendet wird und wir keine spezielle Überladung dieser Funktion zur Verfügung stellen werden, ergibt sich, dass neben dem Kopierkonstruktor auch die Kopierzuweisung existieren sollte. In beiden Fällen werden wir jedoch die compilergenerierten Versionen verwenden, so dass wir hierfür nichts tun müssen.

Um sicherzustellen, dass dies auch möglich ist, müssen wir uns überlegen, welche Datenmember unsere Proxyklassen besitzen müssen und welchen Typ diese haben. Selbstverständlich, muss ein Verweis auf ein matrix-Objekt existieren. Da wir eine Kopierzuweisung erlauben wollen, darf dieser nicht als Referenz implementiert sein. Weiterhin sollen die beiden Proxyklassen, um die wir uns momentan kümmern, einen Verweis auf ein konstantes matrix-Objekt repräsentieren. Der Datentyp für diesen Member muss daher matrix const* lauten. Der Variablenname wird matrix_ lauten. Außerdem benötigen wir natürlich die Zeile oder Spalte, die unser jeweiliges Proxyobjekt repräsentieren soll. Dieser Member muss vom Typ size_type sein und wird pos_ heißen. Alle weiteren, eventuell benötigten Informationen, sind im referenzierten matrix-Objekt enthalten. Entsprechend können wir uns diese, über den Zeiger auf das matrix-Objekt, beschaffen.

Somit kann der Compiler die beiden gewünschten Methoden erstellen und uns bleibt noch, den eigentlichen Konstruktor zur Objekterzeugung zu realisieren. Er muss die beiden Member initialisieren, die wir soeben eingeführt haben. Da für das matrix-Objekt immer ein gültiger Verweis benötigt wird, ist es an dieser Stelle sinnvoll, den Konstruktorparameter als matrix const& zu implementieren. Somit vermeiden wir, dass ein Nullzeiger angegeben werden kann. Bei der Initialisierung des Datenmembers lassen wir uns dann einfach die Adresse geben. Der zweite Parameter sollte vom Typ size_type const& sein. Da size_type typischerweise ein eingebauter Datentyp ist, könnte eine Übergabe mittels „Call by value“ zwar effektiver sein, aber die Compileroptimierung sollte in der Lage sein, dies gegebenenfalls selbst zu erkennen und entsprechend umzusetzen. Mit der Übergabe als Referenz auf const machen wir daher nichts falsch.

// Vor den Proxyklassen - Forward-Deklarationen
template < typename Matrix > class row_proxy;
template < typename Matrix > class column_proxy;

public: // In row_const_proxy
    row_const_proxy(matrix_type const& matrix, size_type const& row):
        matrix_(&matrix), pos_(row){}

public: // In column_const_proxy
    column_const_proxy(matrix_type const& matrix, size_type const& column):
        matrix_(&matrix), pos_(column){}

An Funktionalität benötigen wir den Elementzugriff und die Abfrage, wie viele Elemente die aktuelle Zeile bzw. Spalte besitzt. Außerdem sollte der Nutzer in der Lage sein, abzufragen, auf die wievielte Zeile bzw. Spalte einer Matrix ein Proxyobjekt verweist.

Den Elementzugriff ermöglichen wir zum einen natürlich über den Indexoperator. Zusätzlich werden wir aber in row_const_proxy die Methode column() und in column_const_proxy die Methode row() mit identischer Funktionalität anbieten. Auf diese Weise kann der Nutzer an den Stellen, die Übersichtlichkeit seines Quellcodes erhöhen, an denen es wesentlich und gleichzeitig nicht offensichtlich ist, ob auf ein Elemente innerhalb einer Zeilen oder innerhalb einer Spalte zugegriffen wird.

public: // In row_const_proxy
    value_type const& operator[](size_type const& column_number)const{
        return column(column_number);
    }

    value_type const& column(size_type const& number)const{
        return *(begin() + number);
    }

public: // In column_const_proxy
    value_type const& operator[](size_type const& row_number)const{
        return row(row_number);
    }

    value_type const& row(size_type const& number)const{
        return *(begin() + number);
    }

Beim Elementzugriff wird Ihnen sicher auffallen, dass wir eine Funktion begin() aufrufen, welche jedoch noch nicht existiert. Sie gehört natürlich zum Iteratorinterface des Proxys und wird entsprechend im nächsten Kapitel eingeführt. Die Nutzung der Iteratoren vermeidet, dass wir zweimal über die Positionsberechnung im Container der Matrixklasse nachdenken müssen. Wir vermeiden also Codeverdopplung und erhöhen somit Übersichtlichkeit und Wartbarkeit unseres Quellcodes. Wir lassen die allgemeinen Funktionen jeweils die richtungsspezifischen aufrufen, um noch einmal deutlich zu machen, was passiert.

Ähnlich sieht es bei den Methoden für die Anzahl der Elemente aus. size() wird für beide Proxys eine einheitliche Schnittstelle bieten, während die Methoden columns() bzw. rows() explizit andeuten, ob es sich um die Anzahl der Elemente in einer Zeile oder in einer Spalte handelt. Beachten Sie an dieser Stelle, dass die Methoden mit einem „s“ am Ende, wieder eine Anzahl von Elemente zurückgeben, während sich die Methoden ohne „s“ auf ein konkretes Element beziehen. Die aktuelle Position innerhalb der Matrix werden wir in beiden Proxys über die Methode pos() zurückgeben. Wir könnten die Methode auch position() nennen, aber die Abkürzung „pos“ ist stark verbreitet und wird selbst von unerfahren Programmieren leicht mit „position“ assoziiert, so dass wir getrost die Abkürzung verwenden können.

public: // In row_const_proxy
    size_type const columns()const{ return matrix_const().columns(); }
    size_type const size()const{ return columns(); }

    size_type const pos()const{ return pos_; }

public: // In column_const_proxy
    size_type const rows()const{ return matrix_const().rows(); }
    size_type const size()const{ return rows(); }

    size_type const pos()const{ return pos_; }

Schließlich bleibt noch die Frage zu klären, in welchem Zugriffsbereich unserer Klasse wir die Datenmember unterbringen. Es gibt keinen guten Grund, warum eine abgeleitete Klasse Schreibzugriff auf einen unserer Datenmember haben sollte. Genaugenommen soll auch gar keine Klasse von unseren Proxys abgeleitet werden. Wir werden daher beide Datenmember im private-Bereich unterbringen. Für die Matrix werden wir eine Zugriffsmethode verwenden, so dass wir den Zeiger nicht versehentlich ändern können. Außerdem kann diese gleich die Dereferenzierung unseres Zeigers erledigen. Wir werden die Methode matrix_const() nennen. Sie werden in Kürze erfahren, warum wir nicht einfach matrix() als Namen verwenden.

private: // In row_const_proxy
    matrix_type const& matrix_const()const{ return *matrix_; }

    matrix_type const* matrix_;
    size_type          pos_;

private: // In column_const_proxy
    matrix_type const& matrix_const()const{ return *matrix_; }

    matrix_type const* matrix_;
    size_type          pos_;

Gemeinsamkeiten

Nun sehen Sie natürlich, dass zwei der Methoden und auch die beiden Datenmember für beide Proxyklassen identisch sind. Es wäre natürlich für die Wartbarkeit von Vorteil, wenn wir die identischen Teile auslagern könnten. In der Tat können wir dies mittels Vererbung realisieren, allerdings dürfen wir dabei nicht öffentlich ableiten. Die Ableitung soll einer „ist implementiert in Form von“-Situation entsprechen und daher leiten wir privat ab. Eine protected-Ableitung wäre ebenfalls möglich, jedoch sollen die Proxyklassen am Ende der Vererbungshierarchie stehen. Daher ist eine private Vererbung besser geeignet.

In der gemeinsamen Basisklasse packen wir die Datenmember in den private-Bereich und die Funktionen, die für beide Proxyklassen identisch sind, in den protected-Bereich. Dies betrifft die Zugriffsmethode matrix_const(), sowie die Methode pos(). Nebenbei erreichen wir hierdurch auch, dass die Datenmember innerhalb der Proxyklassen nicht verändert werden können. Lediglich der Zuweisungsoperator darf dies tun. Allerdings auch nur indirekt, indem er den Zuweisungsoperator der Basisklasse aufruft. Auch in dieser Situation, können wir uns auf die compilergenerierten Versionen verlassen.

Die Basisklasse selbst nennen wir line_const_proxy. Der Benutzer muss über diese Klasse nichts wissen, daher werden wir sie im Namensraum detail platzieren. Da wir nicht möchten, dass direkt Objekte von line_const_proxy erzeugt werden können, werden wir die Konstruktoren ebenfalls in den protected-Bereich packen. Um Kopierkonstruktor und Kopierzuweisung müssen wir uns nicht kümmern, da keine Objekte von line_const_proxy erzeugt werden können und eine Verwendung eines Objekts einer abgeleiteten Klasse als Kopierkonstruktorparameter nur bei öffentliche Vererbung möglich ist. Es wird also nicht schaden, wenn die beiden Funktionen im public-Bereich stehen. Den Templateparameter Matrix geben wir einfach an die Basisklasse weiter. Diese sieht somit folgendermaßen aus:

template < typename Matrix >
class line_const_proxy{
protected:
    typedef Matrix                      matrix_type;
    typedef typename Matrix::value_type value_type;
    typedef typename Matrix::size_type  size_type;

    line_const_proxy(matrix_type const& matrix, size_type const& pos):
        matrix_(&matrix), pos_(pos){}

    size_type const pos()const{return pos_;}

    matrix_type const& matrix_const()const{return *matrix_;}

private:
    matrix_type const* matrix_;
    size_type          pos_;
};

In der Folge müssen wir einige Implementierungen unserer beiden Klassen ändern. Die Konstruktoren reichen ihre Parameter nun einfach hoch. Da die Basisklasse ein Template ist, können wir leider keine using-Deklaration für pos() verwenden. Wir müssen stattdessen die pos-Methode der Basisklasse durch eine neue Definition aufrufen lassen. Überall wo bisher die Methode matrix_const() verwendet wird, werden sie beim Übersetzen nun eine Fehlermeldung kassieren. Der Compiler wird sich darüber beschweren, dass er den Bezeichner matrix_const() nicht kennt. Dies liegt daran, dass die Basisklasse ihrerseits eine Klasseninstanz eines Klassentemplates ist.

Um den Compiler zu überreden, einen Namen auch in solchen Basisklassen zu suchen, haben wir zwei Möglichkeiten. Wir können den Bezeichner über den this-Zeiger ansprechen oder die Basisklasse explizit angeben. Letzteres ist viel Schreibarbeit und oft auch schlecht zu lesen. Außerdem kann es in Zusammenhang mit Polymorphie gelegentlich zu unerwünschten Ergebnissen führen. Darauf wollen wir jedoch an dieser Stelle nicht näher eingehen. Dennoch sollten Sie sich angewöhnen, diese Art des Aufrufs wirklich nur dann zu nutzen, wenn sie auch notwendig ist. Wenn Sie versuchen von außerhalb auf einen Bezeichner aus einer Basisklasse zuzugreifen, haben Sie diesen Effekt nicht. Diesbezüglich müssen Sie sich um den späteren Nutzer also keine Gedanken machen.

Innerhalb von Methoden verwenden wir für den Zugriff auf Basisklassenbezeichner den this-Zeiger. Die explizite Angabe der Basisklasse ist beispielsweise beim Zugriff auf Typen aus der Basisklasse notwendig. Um die Übersicht zu erhöhen, macht man üblicherweise die typedefs der Basisklasse, in einer abgeleiteten Klasse, wiederum mittels typedef, unter dem gleichen Namen verfügbar. Von den Änderungen sind in unseren beiden Proxyklassen die nachfolgenden Methoden betroffen. Ihre neuen Implementierungen sehen so aus:

public: // In row_const_proxy
    row_const_proxy(matrix_type const& matrix, size_type const& row):
        detail::line_const_proxy< matrix_type >(matrix, row){}

    size_type const pos()const{ return detail::line_const_proxy< matrix_type >::pos(); }

    size_type const columns()const{ return this->matrix_const().columns(); }

public: // In column_const_proxy
    column_const_proxy(matrix_type const& matrix, size_type const& column):
        detail::line_const_proxy< matrix_type >(matrix, column){}

    size_type const pos()const{ return detail::line_const_proxy< matrix_type >::pos(); }

    size_type const rows()const{ return this->matrix_const().rows(); }

Proxys für nicht-konstante Matrizen

Letztlich verwendete Vererbungshierarchie

Da wir uns nun schon mal die Mühe gemacht haben, Codeverdopplung durch die gemeinsame Basisklasse line_const_proxy zu vermeiden, werden wir natürlich auch für diese beiden Proxys eine gemeinsame Basisklasse schaffen. Da einige der Funktionen wiederum mit denen der Proxys für konstante Matrizen identisch sind, wäre es natürlich angenehm, wenn wir diesen Code wiederum verwenden könnten. Eine Ableitung der Klassen von ihren jeweiligen Äquivalenten für konstante Matrizen, würde uns zwar ein paar Vorteile bieten, aber auch einen unangenehmen Nachteil. Genaugenommen ist dieser Nachteil nicht einmal für uns unangenehm, sondern für den Nutzer unseres Codes. Wenn der Compiler nämlich eine Fehlermeldung bezüglich einer nicht möglichen Typumwandlung, wie in der oben gezeigten Funktion f3(), generiert, dann würde diese bei nicht-öffentlicher Vererbung sehr wahrscheinlich einen Hinweis, auf die nicht zugreifbare Basisklasse enthalten. Der Nutzer erwartet nicht, dass diese Klassen verwandt sind und wenn er noch unerfahren ist, dürfte ihn eine solche Fehlermeldung ziemlich verwirren. Daher sollten wir dies vermeiden.

Wir werden stattdessen eine Klasse line_proxy erstellen und unsere beiden Proxys von dieser ableiten. Die Klasse line_proxy soll natürlich von line_const_proxy abgeleitet werden. Im Gegensatz zur Vererbung der beiden Proxys für konstante Matrizen, muss die Vererbung diesmal geschützt (protected) erfolgen, denn wir wollen von line_proxy ja weitere Klassen ableiten.

line_proxy muss zwei Member besitzen. Zum Einen den üblichen Konstruktor, der eine Matrix und eine Position erhält und zum Anderen eine Zugriffsmethode, die uns eine nicht-konstante Referenz auf das referenzierte Matrixobjekt bietet. Wir werden in dieser Methode die Konstantheit der Matrix mittels const_cast entfernen. Dies ist allerdings nur sicher, wenn wir sicher wissen, dass die Matrix in Wahrheit gar nicht konstant ist. Um dies sicherzustellen, bedienen wir uns des ersten Parameters unseres Konstruktors. Im Gegensatz zum Konstruktor der Basisklasse, wird der Konstruktor von line_proxy eine nicht-konstante Referenz auf ein matrix-Objekt übernehmen. Somit ist es unmöglich, das Objekte von line_proxy eine Matrix referenzieren können, die konstant ist. Gleiches muss natürlich auch für alle Klassen gelten, die von line_proxy abgeleitet werden.

template < typename Matrix >
class line_proxy: protected line_const_proxy< Matrix >{
protected:
    typedef Matrix                      matrix_type;
    typedef typename Matrix::value_type value_type;
    typedef typename Matrix::size_type  size_type;

    line_proxy(matrix_type& matrix, size_type const& pos):
        detail::line_const_proxy< matrix_type >(matrix, pos){}

    matrix_type& matrix()const{ return const_cast< matrix_type& >(this->matrix_const()); }
};

In den abgeleiteten Klassen können wir nun ganz bequem die Methoden matrix() oder matrix_const() verwenden, je nachdem, ob wir Schreibzugriff benötigen oder nicht. Die Ableitung selbst erfolgt jetzt wieder privat. Die meisten Member entsprechen im Wesentlichen denen, der konstanten Proxyklasse und bedürfen daher keiner näheren Betrachtung.

Worüber wir uns noch einmal kurz Gedanken machen müssen, ist die Möglichkeit ein Proxyobjekt, für nicht-konstante Matrizen, implizit in ein entsprechendes Proxyobjekt, für konstante Matrizen, umzuwandeln. Wir können dies realisieren, indem wir den Proxys für nicht konstante Matrizen einen weiteren Konstruktor verpassen und diesen als friend der entsprechenden hiesigen Proxyklassen deklarieren, so dass dieser auf die protected-Methode matrix_const() zugreifen kann. Sehr viel einfacher und übersichtlicher ist es jedoch, wenn wir einfach einen entsprechenden Typcastoperator für die Proxys für konstante Matrizen definieren. Unsere Implementieren sieht somit folgendermaßen aus.

template < typename Matrix >
class row_proxy: private detail::line_proxy< Matrix >{
public:
    typedef Matrix                      matrix_type;
    typedef typename Matrix::value_type value_type;
    typedef typename Matrix::size_type  size_type;

    row_proxy(matrix_type& matrix, size_type const& row):
        detail::line_proxy< matrix_type >(matrix, row){}

    value_type& operator[](size_type const& column_number)const{ return column(column_number); }
    value_type& column(size_type const& number)const{ return *(begin() + number); }

    size_type const columns()const{ return this->matrix_const().columns(); }
    size_type const size()const{ return columns(); }

    size_type const pos()const{ return detail::line_proxy< matrix_type >::pos(); }

    operator row_const_proxy< matrix_type >(){
        return row_const_proxy< matrix_type >(this->matrix_const(), this->pos());
    }
};

template < typename Matrix >
class column_proxy: private detail::line_proxy< Matrix >{
public:
    typedef Matrix                      matrix_type;
    typedef typename Matrix::value_type value_type;
    typedef typename Matrix::size_type  size_type;

    column_proxy(matrix_type& matrix, size_type const& column):
        detail::line_proxy< matrix_type >(matrix, column){}

    value_type& operator[](size_type const& row_number)const{ return row(row_number); }
    value_type& row(size_type const& number)const{ return *(begin() + number); }

    size_type const rows()const{ return this->matrix_const().rows(); }
    size_type const size()const{ return rows(); }

    size_type const pos()const{ return detail::line_proxy< matrix_type >::pos(); }

    operator column_const_proxy< matrix_type >(){
        return column_const_proxy< matrix_type >(this->matrix_const(), this->pos());
    }
};

Elementweise tauschen

Wie bereits erwähnt wurde, werden wir die swap()-Funktion für unsere Proxys nicht selbst überladen. Allerdings wäre es durchaus Hilfreich, wenn wir eine Funktion zur Verfügung stellen würden, welche alle Elemente zweier Zeilen oder Spalten vertauscht. Wir werden diese Funktion element_swap() nennen. Das Vertauschen von Elemente ist natürlich nur für die beiden Proxys sinnvoll, die auf eine nicht-konstante Matrix verweisen. Daher benötigen wir zwei Überladungen, die ihrerseits natürlich Templates sein müssen, um mit allen Klasseninstanzen der jeweiligen Klassentemplats umgehen zu können. Der Quellcode für beide Funktionen ist jedoch identisch, daher wäre es schlechter Stiel, diesen zweimal einzugeben. Wie also lösen wir dieses Dilemma.

Wir können natürlich als Templateparameter einen Typ Proxy übergeben lassen. Dies hat allerdings den gewaltigen Nachteil, dass unsere Funktion dann kompatibel zu allen Typen ist, welche die in der Implementierung verwendeten Member unterstützen. Außerdem werden die Fehlermeldungen für inkompatible Typen sehr unübersichtlich und für unerfahrene Programmierer schwer zu interpretieren. Was wir wollen ist, diese allgemeine Funktion vor dem Nutzer zu verstecken. Die beiden auf die Proxys bezogenen Überladungen können dann diese allgemeine Funktion aufrufen. Wir packen die allgemeine Funktion daher in den Namensraum detail.

namespace detail{
    template < typename Proxy >
    inline void element_swap_template(Proxy const& lhs, Proxy const& rhs){
        typedef typename Proxy::iterator iterator;
        using std::swap;

        if(lhs.size() != rhs.size()){
            throw error::size_unequal("mitrax::element_swap_template<>()", lhs.size(), rhs.size());
        }

        for(
            iterator i = lhs.begin(), j = rhs.begin();
            i != lhs.end();
            ++i, ++j
        ){
            swap(*i, *j);
        }
    }
}

template < typename Matrix >
inline void element_swap(row_proxy< Matrix > const& lhs, row_proxy< Matrix > const& rhs){
    detail::element_swap_template(lhs, rhs);
}

template < typename Matrix >
inline void element_swap(column_proxy< Matrix > const& lhs, column_proxy< Matrix > const& rhs){
    detail::element_swap_template(lhs, rhs);
}

Zum eigentlichen Vertauschen verwenden wir selbstverständlich wieder das Iteratorinterface. Die Ausnahmeklasse error::size_unequal wird später behandelt. Sie ist von std::logic_error abgeleitet. Wie Ihnen vielleicht auffällt, müssen wir uns um den Namen oder die einfache Nutzung von element_swap_template viel weniger Gedanken machen als sonst. Denn außer uns und jenen Menschen, die unseren Code später möglicherweise warten müssen, wird nie jemand von dieser Funktion erfahren. Natürlich heißt dies nicht, dass Sie sich überhaupt keine Gedanken machen müssen. Eine kleine Anzahl von Leuten wird die Funktion schließlich immer noch zu Gesicht bekommen und diese sollten schon verstehen können, was vor sich geht.

Iteratoren für die Proxys

In diesem Kapitel werden wir uns mit der Erstellung eigener Iteratorklassen beschäftigen und die Schnittstellen der Proxyklassen vervollständigen. Der Nutzer von mitrax sollte mit den Iteratorklassen selbst, keinen direkten Kontakt haben, daher werden wir diese vollständig im Namensraum detail platzieren. Wir werden diese Tatsache im folgenden nicht jedes mal explizit wieder erwähnen. Sofern nicht anderes angegeben, gehören die Inhalte dieses Kapitels in die Datei proxy_iterator.hpp. Da alles in dieser Datei im Namensraum detail liegt, befindet sich proxy_iterator.hpp in einem Unterverzeichnis detail/.

Einführung zu Iteratoren

Ehe wir uns der Entwicklung unserer Iteratorklassen widmen, wollen wir uns ansehen, was Iteratoren eigentlich sind. Vielleicht ist Ihnen bekannt, dass jeder Zeiger auch ein Iterator ist. Jedoch ist nicht jeder Iterator auch ein Zeiger. Iteratoren sind abstrakte Objekte, die, je nachdem zu welcher Iteratorkategorie sie gehören, bestimmte Eigenschaften besitzen müssen. Jedes Objekt, das die Eigenschaften einer Iteratorkategorie erfüllt, ist ein Iterator der entsprechenden Kategorie. Zeiger erfüllen beispielsweise alle Eigenschaften, die ein Random-Access-Iterator besitzen muss.

C++ kennt standardmäßig fünf Iteratorkategorien. Die einfachsten sind Input- und Output-Iteratoren. Darüber stehen die Forward-Iteratoren, sie erfüllen alle Anforderungen, die an Input-Iteratoren gestellt werden. Die Bidirectional-Iteratoren erfüllen alle Anforderungen, die an Forward-Iteratoren gestellt werden und schließlich erfüllen Random-Access-Iteratoren alle Anforderungen, die an Bidirectional-Iteratoren gestellt werden. Jede dieser Kategorien macht natürlich noch zusätzlich Vorgaben, welche Ausdrücke nutzbar sein müssen. Iteratoren die zusätzlich die Anforderungen erfüllen, die an Output-Iteratoren gestellt werden, bezeichnet man als veränderliche Iteratoren, alle anderen werden als konstante Iteratoren bezeichnet. Jede dieser Iteratorkategorien wird durch ein sogenanntes Iterator-Tag repräsentiert. Die fünf Iterator-Tags, die in der Standard-Headerdatei iterator definiert sind, hängen wie folgt zusammen:

struct input_iterator_tag{};
struct output_iterator_tag{};
struct forward_iterator_tag: public input_iterator_tag{};
struct bidirectional_iterator_tag: public forward_iterator_tag{};
struct random_access_iterator_tag: public bidirectional_iterator_tag{};

Vielleicht fragen Sie sich, warum forward_iterator_tag nicht auch von output_iterator_tag abgleitet ist. Dies liegt daran, dass die Ausgabe auf einen Iterator, wie bereits erwähnt, zusätzlich zur Eingabe erfüllt sein kann. Nehmen wir als Beispiel die Iteratoren des Containers std::vector. Dieser bietet Random-Access-Iteratoren an. Iteratoren vom Typ std::vector< T >::iterator sind sowohl Input-, als auch Output-Iteratoren, wohingegen Iteratoren vom Typ std::vector< T >::const_iterator ausschließlich Input-Iteratoren sind. Obgleich es sich auch bei diesen um Random-Access-Iteratoren handelt, ist ein Schreiben über diese unmöglich. Eben deshalb werden diese Iteratoren auch als konstant bezeichnet, während es sich bei std::vector< T >::iterator um veränderliche Iteratoren handelt.

Für alle Iteratoren sind fünf Typen als sogenannte Iterator-Traits (auf Deutsch etwa Eigenschaften oder Charakteristika) definiert. Diese können über das Template std::iterator_traits< Iterator > abgefragt werden. value_type ist der Typ, der bei einer Dereferenzierung zurückgegeben wird. reference ist eine Referenz und pointer ein Zeiger auf diesen Typ. difference_type ist ein vorzeichenbehafteter ganzzahliger Datentyp, der eine Entfernung zwischen zwei Iteratoren aus dem gleichen Bereich beschreibt. iterator_category ist ein typedef auf eines der fünf Iterator-Tags. Wenn wir einen neuen Iterator entwerfen, müssen wir das Template std::iterator_traits nicht spezialisieren. Wir müssen diese fünf typedefs lediglich innerhalb unserer Iteratorklassen anbieten. Die allgemeine Implementation von std::iterator_traits sieht nämlich folgendermaßen aus:

template< typename Iterator >
struct iterator_traits{
    typedef typename Iterator::difference_type   difference_type;
    typedef typename Iterator::value_type        value_type;
    typedef typename Iterator::pointer           pointer;
    typedef typename Iterator::reference         reference;
    typedef typename Iterator::iterator_category iterator_category;
};

Ein Iterator b wird als, von einem Iterator a aus, erreichbar bezeichnet, wenn durch eine endliche Anwendung von ++a, die Bedingung b == a wahr wird. Die beiden Iteratoren befinden sich dann in der gleichen Sequenz. Jeder Iterator, für den der Ausdruck *a ein gültiges Objekt liefert, wird als dereferenzierbar bezeichnet. Für jede Sequenz von Iteratoren, muss ein Iterator existieren, der hinter das letzte Element zeigt. Dieser muss nicht dereferenzierbar sein.

Nun wollen wir uns noch die Eigenschaften ansehen, die Iteratoren der verschiedenen Kategorien erfüllen müssen. Alle Iteratoren müssen einen value_type besitzen, der kopierkonstruierbar, kopierzuweisbar und destruierbar ist. Außerdem müssen zwei Objekte von value_type mittels swap() vertauschbar sein. Beachten Sie, dass dies nicht zwingend std::swap() sein muss. Wenn iterator_type der Typ eines Iterators und a ein Objekt dieses Typs ist, dann muss der Ausdruck *a eine Referenz auf value_type zurückgeben, vorausgesetzt, der Iterator zeigt auf ein gültiges Objekt. Andernfalls ist das Verhalten, wie bei ungültigen Zeigern, undefiniert. Der Ausdruck ++a muss eine Referenz auf iterator_type zurückgeben.

Für zwei Input-Iteratoren a und b des gleichen Typs muss der Vergleichsoperator auf Gleichheit definiert sein. Der Vergleichsoperator auf Ungleichheit muss ebenfalls definiert sein und dem Verhalten des Ausdrucks !(a == b) entsprechen. Beide müssen einen Typ zurückgeben, der implizit in bool konvertiert werden kann. Der Ausdruck *a muss einen Typ zurückgeben, der implizit in value_type konvertierbar ist. Wenn a dereferenzierbar ist, müssen die Ausdrücke a->m und (*a).m identisch sein. Nach Anwendung des Ausdrucks ++a auf einen dereferenzierbaren Iterator a, muss a entweder wieder dereferenzierbar sein, oder hinter das letzte Element einer Sequenz zeigen. Die Ausdrücke (void)++a und (void)a++ müssen identisch sein. Der Ausdruck *a++ muss einen Typ zurückgeben, der implizit in value_type konvertiert werden kann. Außerdem muss er dem Verhalten von { value_type tmp = *a; ++a; return tmp;} entsprechen. Input-Iteratoren dürfen nur einmal gelesen werden und ihr value_type muss nicht kopierzuweisbar sein.

Ein Output-Iterator a vom Typ iterator_type muss den Ausdruck *a = value zulassen. Der Rückgabetyp dieses Ausdrucks ist nicht spezifiziert. Die übliche Konvention besagt natürlich, dass es sich um eine Referenz auf *a handeln sollte, dies ist aber keine Anforderung, die von Iteratoren gestellt wird. Der Ausdruck ++a muss eine Referenz auf iterator_type sein. Der Rückgabetyp des Ausdrucks a++ muss implizit nach iterator_type const& konvertierbar sein und der Ausdruck muss dem Verhalten von { iterator_type tmp = a; ++a; return tmp;} entsprechen. Der Ausdruck *a++ = value muss spezifiziert sein. Der Rückgabetyp dieses Ausdrucks ist wiederum nicht spezifiziert. Auf Output-Iterator darf nur einmal geschrieben werden.

Forward-Iteratoren dürfen beliebig oft gelesen und, sofern sie veränderlich sind, auch beschrieben werden. Sie müssen defaultkonstruierbar sein. Falls iterator_type ein veränderlicher Iterator ist, so ist reference äquivalent zu value_type&, andernfalls zu value_type const&. Für zwei dereferenzierbare Forward-Iteratoren a und b impliziert a == b gleich true, dass auch ++a == ++b wahr sein muss. Wenn a und b dereferenzierbar sind, so darf a == b ausschließlich dann wahr sein, wenn a und b zur gleichen Sequenz gehören. Der Typ des Ausdrucks a++ muss implizit in value_type const& konvertierbar sein und der Ausdruck muss dem Verhalten von { iterator_type tmp = a; ++a; return tmp;} entsprechen. Der Rückgabetyp des Ausdrucks *a++ muss vom Typ reference sein.

Mit Bidirectional-Iteratoren kann man eine Sequenz sowohl vorwärts, als auch rückwärts durchlaufen. Sie entsprechen Forward-Iteratoren und erfüllen weiterhin die nachfolgenden Bedingungen. --a gibt eine Referenz auf iterator_type zurück. Der Ausdruck ist anwendbar, wenn ein Iterator b existiert, für den a == ++b wahr ist. Wenn a dereferenzierbar ist, muss außerdem --(++a) == a wahr sein und wenn --a == --b wahr ist, muss auch a == b wahr sein. Der Ausdruck a-- muss einen Rückgabetyp besitzen, der implizit in iterator_type const& konvertierbar ist und er muss dem Verhalten von { iterator_type tmp = a; --a; return tmp;} entsprechen. Der Rückgabetyp des Ausdrucks *a-- muss reference sein.

Die umfangreichsten Ansprüche stellen Random-Access-Iterator, sie erfüllen alle Anforderungen der Bidirectional-Iteratoren und bieten einen wahlfreien Zugriff auf Elemente einer Sequenz. Wenn n vom Typ difference_type ist, muss der Ausdruck a += n eine Referenz auf iterator_type zurückgeben und dem Verhalten von { difference_type m = n; if(m >= 0) while(m--) ++a; else while(m++) --a; return a;} entsprechen. Die Ausdrücke a + n und n + a müssen ein Objekt vom Typ iterator_type zurückgeben und dabei dem Verhalten von { iterator_type tmp = a; return a += n;} entsprechen. Weiterhin muss a + n == n + a wahr sein. Der Ausdruck a -= n muss den Rückgabetyp iterator_type& besitzen und sich wie return a += -n; verhalten. Der Ausdruck a - n muss ein Objekt vom Typ iterator_type zurückgeben und dem Verhalten von { iterator_type tmp = a; return tmp -= n;} entsprechen. Vorausgesetzt es existiert ein Wert n vom Typ difference_type, für welchen a + n == b wahr ist, so muss der Ausdruck b - a ein Objekt vom Typ difference_type zurückgeben, welches dem Wert n entspricht. Der Ausdruck a[n] muss ein Objekt zurückgeben, das implizit in reference konvertiert werden kann und er muss dem Verhalten von *(a + n) entsprechen. Schließlich müssen die vier übrigen Vergleichsoperatoren für Random-Access-Iterator definiert sein. Alle vier müssen ein Objekt zurückgeben, das implizit in bool konvertiert werden kann. a < b muss dem Verhalten von b - a > 0 entsprechen. a > b muss dem Verhalten von b < a entsprechen. a >= b muss dem Verhalten von !(a < b) entsprechen und schließlich muss a <= b dem Verhalten von !(a > b) entsprechen.

Mit diesem Wissen, kennen Sie zwar noch nicht alle Details der C++-Iteratoren, aber Sie haben schon einen guten Überblick und sind gerüstet, um Ihre ersten eigenen Iteratorklassen zu schreiben. Wenn Sie dereinst tatsächlich selbst eine Iteratorklasse schreiben müsse, dann besorgen Sie sich am besten einen C++-Standard, in welchem Sie sämtlich Details noch einmal nachlesen können. Unter der Adresse http://www.open-std.org/JTC1/SC22/WG21/ finden Sie die Website der Arbeitsgruppe das C++-Standardkomitees. Den aktuellen Standard bekommen Sie dort zwar nicht, aber die Arbeitsentwürfe (Working Drafts) können frei eingesehen werden. Dies eröffnet ihnen übrigens auch die Möglichkeit, sich über die Pläne für kommende Standards auf dem laufenden zu halten, sofern Sie dies Wünschen.

Allgemeine Basis

Sie haben nun eine ganze Menge sehr trockener Theorie studiert. Sicher ist Ihnen dabei dennoch aufgefallen, dass viele der aufgeführten Ausdrücke direkt anhand der Ausdrücke implementiert werden können, deren Verhalten sie entsprechen sollen. Dies tatsächlich zu tun, hat für uns zwei wesentliche Vorteile. Zum Ersten haben wir weniger Schreibarbeit und zum Zweiten vermeiden wir dadurch auch Codeverdopplung. Da diese Operationen jedoch obendrein für alle Iteratoren den gleichen Quellcode besitzen, lohnt es sich, eine allgemeine Basisklasse zu schreiben, welche von den eigentlichen Iteratorklassen nur noch geerbt werden muss.

In dieser Basisklasse muss der Typ der abgeleiteten Klasse bekannt sein. Dies realisieren wir, indem wir diese, als Templateparameter an die Basisklasse hochreichen. Auf diese Weise ist auch gleich sichergestellt, dass jede dieser Basisklasseninstanzen zu genau einer Iteratorklasse gehört. Wie wir bereits festgelegt haben, werden wir Random-Access-Iteratoren für die Proxys bereitstellen. Da wir ja soeben die verschiedenen Iteratorkategorien durchgegangen sind, werden wir aber nicht einfach eine Basisklasse verwenden, sondern drei Klassen, in denen jeweils die Operatoren für Forward-Iteratoren, Bidirectional-Iteratoren und Random-Access-Iterator definiert sind. Auf diese Weise machen wir uns noch einmal klar, welche Operatoren zu welcher Kategorie gehören. Prinzipiell könnte man von den jeweiligen Klassen dann natürlich auch andere Iteratorklassen, als nur jene für unsere Proxys ableiten.

Für Forward-Iteratoren können wir den Post-Inkrement-Operator und den Ungleichheitsoperator verallgemeinert nutzen. Für den Ungleichheitsoperator haben Sie bereits gelernt, dass es schlechter Stiel ist, wenn nur der zweite Parameter eine implizite Typumwandlung unterstützt. Daher werden wir diesen als friend-Funktion innerhalb der Klasse definieren. Den Post-Inkrement-Operator würden wir auf den ersten Blick als Member deklarieren. Allerdings werden Sie spätestens nach der Definition des Pre-Inkrement-Operators innerhalb der abgeleiteten Iteratorklasse vor einem Problem stehen. Die Prefix- und Postfix-Versionen dieses Iterators werden durch einen ungenutzten int-Parameter unterschieden. Der Compiler behandelt Sie daher wie eine Funktionsüberladung und wie Sie sich sich hoffentlich erinnern werden, verdeckt die Redeklaration einer Methode in einer abgeleiteten Klasse, alle Deklarationen in den Basisklassen. Folglich wäre der Operator nicht mehr sichtbar, wenn wir ihn als Member implementieren. Nehmen wir die Deklaration als friend-Funktion innerhalb der Klasse vor, so besteht dieses Problem nicht. Um eine unerwünschte implizite Typumwandlung für den ersten Parameter müssen wir uns dabei nicht sorgen, denn dieser ist eine nicht-konstante Referenz auf die abgeleitete Iteratorklasse und für nicht-konstante Referenzen kann keine implizite Typumwandlung erfolgen. Dass die Funktionen mit der Basisklasse befreundet sind, muss uns kein Kopfzerbrechen bereiten, den Freundschaft wird ja nicht vererbt.

Somit bleibt noch die Frage zu klären, wie wir das direkte Erstellen von Objekten unserer Basisklassen verhindern. Die Antwort darauf lautet, wir Deklarieren die Konstruktoren im protected-Bereich. Die Klassen beinhalten keine Datenmember, daher müssen die Konstruktoren nichts tun. Im Grunde würde es daher genügen, den Standardkonstruktor zu definieren. Da unsere abgeleiteten Iteratorklassen jedoch den compilergenerierten Kopierkonstruktor benutzen könnten und dieser den Kopierkonstruktor der Basisklasse aufruft, ist auch die Deklaration des Kopierkonstruktors notwendig. An dieser Stelle sein noch einmal darauf hingewiesen, dass ein selbst definierter Kopierkonstruktor, sofern nicht anderes angegeben, den Standardkonstruktor der Basisklasse aufruft. Folglich wäre es also ausreichend, wenn wir die Definition des Kopierkonstruktors nur für unsere Random-Access-Iterator-Basisklasse angeben und in den anderen beiden, lediglich eine Deklaration verwenden. Da es jedoch, zumindest prinzipiell, möglich sein sollte, auch von den anderen beiden Basisklassen konkrete Iteratoren der entsprechenden Iteratorkategorie abzuleiten, werden wir auch hier eine Definition schreiben. Man weiß ja nie, was in einer späteren Version noch dazukommt. Außerdem besteht der zusätzliche Schreibaufwand in einem einzigen Zeichen. Statt eines Semikolons geben wir leere geschweifte Klammern an. Weiterhin schadet es auch nicht, wenn Sie explizit den Standard- oder Kopierkonstruktor der Basisklasse aufrufen. Je nach Compilereinstellung vermeiden Sie dadurch Warnungen. Wir werden dies hier aus Platzgründen jedoch nicht tun.

template < typename Derived >
class forward_iterator_base{
protected:
    forward_iterator_base(){}
    forward_iterator_base(forward_iterator_base const&){}

public:
    friend Derived const operator++(Derived& self, int){
        Derived tmp(self); ++self; return tmp;
    }

    friend bool operator!=(Derived const& lhs, Derived const& rhs){
        return !(lhs == rhs);
    }
};

Über die Basisklasse für Bidirectional-Iteratoren gibt es nicht viel zu sagen. Sie spezifiziert den Post-Dekrement-Operator in äquivalenter Weise zum Post-Inkrement-Operator von forward_iterator_base und ist natürlich von forward_iterator_base abgeleitet. Der Templateparameter wird dabei an die Basisklasse weitergegeben.

template < typename Derived >
class bidirectional_iterator_base: public forward_iterator_base< Derived >{
protected:
    bidirectional_iterator_base(){}
    bidirectional_iterator_base(bidirectional_iterator_base const&){}

public:
    friend Derived const operator--(Derived& self, int){
        Derived tmp(self); --self; return tmp;
    }
};

Die Basisklasse für Random-Access-Iteratoren erhält noch einen zweiten Templateparameter. Da wir die Plus- und Minus-Operatoren, welche mit einem Iterator und einer Differenz aufgerufen werden, implementieren möchten, benötigen wir den difference_type. Beachten Sie, dass Sie sich diesen nicht mittels typename aus dem Templateparameter Derived extrahieren können. Die abgeleitete Klasse Derived kann zum Zeitpunkt der Basisklasseninstantiierung noch nicht instantiiert sein. Folglich ist es unmöglich, auf deren Definition zuzugreifen. Die drei erwähnten Operatoren werden natürlich auch wieder als friend-Funktionen innerhalb der Klasse definiert. Ebenso die vier verbleibenden Vergleichsoperatoren. Anders sieht es beim operator-=() aus, diesen werden wir als Member implementieren, weil nichts dagegen spricht. Damit der genutzte operator+=(), in der abgeleiteten Klasse gefunden werden kann, muss der this Zeiger in diese Umgewandelt werden. Da wir mit Sicherheit wissen, dass das aktuelle Objekt in Wahrheit vom Typ der abgeleiteten Iteratorklasse ist, können wir die Umwandlung bedenktenlos mit static_cast vornehmen.

template < typename Derived, typename DifferenceType >
class random_access_iterator_base: public bidirectional_iterator_base< Derived >{
protected:
    random_access_iterator_base(){}
    random_access_iterator_base(random_access_iterator_base const&){}

public:
    friend bool operator<(Derived const& lhs, Derived const& rhs){
        return rhs - lhs > DifferenceType();
    }

    friend bool operator>(Derived const& lhs, Derived const& rhs){
        return rhs < lhs;
    }

    friend bool operator<=(Derived const& lhs, Derived const& rhs){
        return !(lhs > rhs);
    }

    friend bool operator>=(Derived const& lhs, Derived const& rhs){
        return !(lhs < rhs);
    }

    Derived& operator-=(DifferenceType const& difference){
        return static_cast< Derived& >(*this) += -difference;
    }

    friend Derived const operator+(Derived lhs, DifferenceType const& rhs){
        return lhs += rhs;
    }

    friend Derived const operator+(DifferenceType const& rhs, Derived lhs){
        return lhs += rhs;
    }

    friend Derived const operator-(Derived lhs, DifferenceType const& rhs){
        return lhs -= rhs;
    }
};

Somit haben wir eine Klasse, von der wir unsere vier Iteratorklassen ableiten können und die uns in der Folge eine menge Arbeit abnimmt. Wie ihnen sicher aufgefallen ist, verwenden wir in diesen Basisklassen sehr intensiv eine Abart der Technik, die im Kapitel über den Datentyp dimension vorgestellt wurde, um für Funktionstemplates eine implizierte Typumwandlung für beide Parameter zu ermöglichen. Mit der Verwendung bei den Postfix-Operatoren haben Sie ein weiteres Anwendungsfeld dieser Technik kennen gelernt. Dass die Rückgabetypen der Postfix-Inkrement- und -Dekrement-Operatoren, sowie der Plus- und Minus-Operatoren konstant sind, widerspricht zwar den Vorgaben, die für Iteratoren eigentlich im Standard gemacht werden, aber es wurde schon im Kapitel über die Proxyklassen gezeigt, dass wir uns auf diese Weise einiges an Ärger ersparen und real dürfte es wohl kaum einen Fall geben, in dem unsere konstanten Rückgabetypen ein Problem darstellen.

Basis der Iteratorklassen für konstante und nicht-konstante Matrizen

Bevor wir mit der Implementierung der konkreten Iteratorklassen beginnen, sollten wir uns noch kurz Gedanken darüber machen, zu welchem Objekt ein Iteratorobjekt gehört. Wir könnten jeden Iterator an ein Proxyobjekt binden, bedenken Sie jedoch, was dies bedeuten würde. Die Proxyobjekte sind meist selbst nur temporäre Objekte. Wenn wir einen Iterator intern auf einen Proxy verweisen lassen, dann wird es nicht selten passieren, dass dieser Proxy schneller wieder inexistent ist, als der erzeugte Iterator. In der Folge wäre der Iterator ungültig, obwohl die Zeile oder Spalte, auf die er sich bezieht, in der Matrix immer noch existiert. Außerdem wären die Iteratoren verschiedener Proxyobjekte, welche auf die gleiche Zeile oder Spalte verweise, nicht in der gleichen Sequenz. Beides macht uns deutlich, dass dieses Vorgehen eine sehr schlechte Idee wäre. Wir binden die Iteratoren stattdessen an die Matrizen, auf welche die Proxyklassen verweisen. Auf diese Weise umgehen wir beide Probleme.

Der zweite Punkt, über den wir uns vorweg Gedanken machen können, sind die Unterschiede zwischen den Iteratoren für konstante und nicht-konstante Proxys. Bei den Proxyklassen haben wir ja bereits festgestellt, dass sich die dortigen Versionen sehr ähnlich sind. Bei den Iteratorklassen ist dies noch mehr der Fall. Die Versionen für konstante Matrizen besitzen einen zusätzlichen Konstruktor für die implizite Typumwandlung aus den Versionen für nicht-konstante Matrizen. Alle übrigen Implementierungen unterscheiden sich lediglich im Typ, der auf das Matrixobjekt verweist. Quelltextmäßig ist die Implementierung völlig identisch. Folglich können wir diese in einem gemeinsamen Basisklassentemplate zusammenfassen, dem wir lediglich die Typen als Parameter übergeben, in denen sich die beiden Versionen unterscheiden.

Natürlich benötigt auch diese Basisklasse wieder die abgeleitete Klasse als Templateparameter. Wenn wir schließlich unsere Versionen für konstante und nicht konstante Matrizen öffentlich von dieser Klasse ableiten, dann müssen wir in diesen nur noch die Konstruktoren definieren und haben für alle benötigten Operatoren eine funktionsfähige Version geerbt.

Diese Technik hat eine ganze Reihe von Vorteilen. Offensichtlich ist natürlich, dass wir uns Schreibarbeit ersparen. Außerdem vermeiden wir Codeverdopplung, was die Wartbarkeit deutlich vereinfacht. Da der Compiler aufgrund des Templates sehr leicht erkennen kann, welche Teile der Klasseninstantiierung immer identisch sind, ermöglichen wir ihm eine gute Gelegenheit zu Optimierung. Letzten Endes verdeutlichen wir einem Leser unsere Quellcodes natürlich auch noch, dass sich diese beiden Versionen, bis auf die Datentypen, identisch verhalten.

Iteratoren für Zeilenproxys

Wir werden, unseren eben angestellten Überlegungen entsprechend, die eigentliche Implementierung der Operatoren innerhalb einer typunabhängigen Basisklasse vornehmen. Zunächst müssen wir uns jedoch darüber im klaren sein, welche Datenmember unsere Zeileniteratoren benötigen. Da alle Elemente einer Zeile im Datenfeld der Matrix hintereinander liegen, können wir die Iteratoren einer Zeile auf eine Teilsequenz der Iteratoren des Datenfeldes abbilden. Wir werden also einen Datenmember vom Typ der Iteratoren der Matrixklasse benötigen, denn diese reicht ja einfach die Iteratoren ihres Datenfeldes durch. Dies allein genügt anscheinend bereits für die Implementierung der Member.

Allerdings wird an den Gleichheitsoperator noch die Bedingung gestellt, dass das Ergebnis für zwei dereferenzierbare Iteratoren dann und nur dann true sein darf, wenn diese auch zur gleichen Sequenz gehören. Wir müssen also prüfen, ob wir möglicherweise auch noch einen Vergleich für die Zeile durchführen müssen, auf die sich die beiden Operatorargumente beziehen, denn diese Information ist im Iterator der Matrix ja nicht enthalten. Glücklicherweise kommt uns hier die Vorbedingung dieser Anforderung zu gute. Die Iteratoren müssen beide dereferenzierbar sein und wir geben keine Garantie dafür, dass ein Iterator, der außerhalb der Zeile liegt, für die er erzeugt wurde, dereferenzierbar ist. Das Verhalten des Ausdrucks *iter ist somit undefiniert und damit ist der Iterator iter per Definition nicht dereferenzierbar, auch wenn das Zufallsbedingt klappen kann. Wenn wir also in unserem Vergleichsoperator nur auf die Gleichheit der Matrixiteratoren prüfen und dieser für zwei Iteratoren, aus unterschiedlichen Zeilen true ergibt, so war mindestens einer der beiden Iteratoren außerhalb seines gültigen Bereichs und somit per Definition nicht dereferenzierbar. Unter diesen Umständen ist auch die Rückgabe des Vergleichsoperators nicht definiert. Wir können völlig beliebig true oder false zurückgeben oder das Programm mit einem Ausnahmefehler beenden oder abstürzen lassen, wenn wir dies wünschen würden. Dieses Verhalten ist übrigens äquivalent zu dem, gewöhnlicher Zeiger. Auch dort kann ein Zeiger ja ohne weiteres ein Element hinter einem Array referenzieren. Was bei der Dereferenzierung passiert ist allerdings dem Zufall überlassen.

Es bleibt also bei dieser einen Membervariable. Die Konstruktoren werden wir so gestalten, dass ein Matrixiterator übergeben wird. Die Proxymethoden begin() und end() können dann die korrekte Position des entsprechenden Matrixiterators berechnen und aus diesen, ein Zeileniteratorobjekt erzeugen. Für den zwar unwahrscheinlichen, aber nicht unmöglichen Fall, dass der Matrixiteratortyp ein eingebauter Datentyp ist, werden wir ihn explizit durch ein standardkonstruiertes Objekt initialisieren. Da wir nicht wollen, dass von dieser Klasse direkt Objekte erzeugt werden können, werden wir die Konstruktoren wiederum in protected-Bereich deklarieren. Da wir von dieser Klasse öffentlich ableiten wollen, müssen wir auch den Kopierkonstruktor im protected-Bereich deklarieren. Leider hat dies zur Folge dass wir ihn diesmal tatsächlich selbst schreiben müssen, denn die compilergenerierte Version würde im öffentlichen Bereich stehen. Da die Basisklassen dieser Basisklasse keine Datenmember besitzen, müssen wir uns zumindest nicht die Mühe machen, deren Kopierkonstruktoren aufzurufen. Genau wie wir es in diesen Basisklassen bereits getan haben, wird unser Kopierkonstruktor einfach implizit den Standardkonstruktor der unmittelbaren Basisklasse aufrufen.

Natürlich müssen wir für unsere Iteratoren die fünf typedefs bereitstellen, die für die Iterator-Traits benötigt werden. Die Iteratorkategorie ist natürlich Random-Access. Für die anderen vier Typen bedienen wir uns bei den Iteratoren der Matrixklasse. Da wir unsere Zeileniteratoren auf diese abbilden ist es nur folgerichtig, wenn wir auch deren Iterator-Traits übernehmen.

Unsere Basisklasse muss somit zwei Templateparameter besitzen. Zum Ersten die konkrete abgeleitete Iteratorklasse und zum Zweiten natürlich den konkreten Iteratortyp der Matrixklasse. Dieser kann ja sowohl matrix< T >::iterator, als auch matrix< T >::const_iterator sein und wie an anderer Stelle schon erwähnt, kann auf Informationen aus der abgeleiteten Klasse, zum Zeitpunkt der Basisklasseninstantiierung, noch nicht zugegriffen werden. Wir müssen diese Information daher zwingend als Templateparameter übergeben.

Die Implementierung der übrigen Operatoren enthält keine großen Überraschungen, im wesentlichen reichen Sie alle ihre Parameter an die entsprechende Operation des Matrixiterators weiter. Der Datenmember ist im protected-Bereich deklariert, damit die abgeleitete Iteratorklasse darauf zugreifen kann. Das <ganze sieht somit wie Folgt aus:

template < typename Derived, typename MatrixIterator >
class row_iterator_base:
    public random_access_iterator_base< Derived, typename MatrixIterator::difference_type >
{
public:
    typedef typename MatrixIterator::value_type      value_type;
    typedef typename MatrixIterator::difference_type difference_type;
    typedef typename MatrixIterator::pointer         pointer;
    typedef typename MatrixIterator::reference       reference;
    typedef std::random_access_iterator_tag          iterator_category;

    reference operator*()const{return *pos_;}
    pointer operator->()const{return pos_;}

    Derived& operator++(){ ++pos_; return static_cast< Derived& >(*this); }
    Derived& operator--(){ --pos_; return static_cast< Derived& >(*this); }

    friend bool operator==(Derived const& lhs, Derived const& rhs){ return lhs.pos_ == rhs.pos_; }

    Derived& operator+=(difference_type const& difference){
        pos_ += difference; return static_cast< Derived& >(*this);
    }

    friend difference_type const operator-(Derived const& lhs, Derived const& rhs){
        return lhs.pos_ - rhs.pos_;
    }

    reference operator[](difference_type const& index)const{ return *(pos_ + index); }

protected:
    row_iterator_base(): pos_(MatrixIterator()){}
    row_iterator_base(MatrixIterator const& pos): pos_(pos){}
    row_iterator_base(row_iterator_base const& iter): pos_(iter.pos_){}

    MatrixIterator pos_;
};

Alles, was wir jetzt noch tun müssen, ist unsere konkreten Iteratorklassen jeweils von einer Klasseninstanz des Templates row_iterator_base öffentlich abzuleiten und in den abgeleiteten Klassen die benötigten Konstruktoren, sowie für row_iterator den operator row_const_iterator() zu definieren. Sämtliche Operatoren und Typen werden aus dieser Klasseninstanz geerbt. Unsere beiden konkreten Iteratorklassen, sehen somit folgendermaßen aus.

template < typename Matrix >
class row_const_iterator:
    public row_iterator_base< row_const_iterator< Matrix >, typename Matrix::const_iterator >
{
private:
    typedef row_iterator_base< row_const_iterator< Matrix >, typename Matrix::const_iterator > base;

public:
    row_const_iterator(){}
    row_const_iterator(typename Matrix::const_iterator const& pos): base(pos){}
};

template < typename Matrix >
class row_iterator:
    public row_iterator_base< row_iterator< Matrix >, typename Matrix::iterator >
{
private:
    typedef row_iterator_base< row_iterator< Matrix >, typename Matrix::iterator > base;

public:
    row_iterator(){}
    row_iterator(typename Matrix::iterator const& pos): base(pos){}

    operator row_const_iterator< Matrix >()const{
        return row_const_iterator< Matrix >(this->pos_);
    }
};

Die privaten base-typedefs dienen lediglich der besseren Übersicht, da der Basisklassenname sehr lang wird.

Iteratoren für Spaltenproxys

Das Vorgehen für die Spaltenproxys ist vom Prinzip her vollkommen äquivalent. Allerdings können wir diesmal nicht einfach eine Teilsequenz durchreichen. Wir müssen uns stattdessen selbst Gedanken über eine einigermaßen effiziente Implementierung machen. Wir könnten intern beispielsweise eine Variable verwalten, welche eine Position speichert, die vom Anfang des in matrix enthaltenen Datenfeldes aus gemessen wird. Wenn wir diese nach der Initialisierung immer nur noch genau um ein vielfaches der Zeilenlänge, also der Anzahl der Spalten, verschieben, so erreichen wir genau alle gültigen Positionen innerhalb einer Spalte.

Falls Sie nun auf die Idee kommen, einen Matrixiterator dafür zu verwenden, dann denken Sie noch einmal darüber nach, wie dieser sich verhält, wenn er über das Ende seiner gültigen Sequenz hinaus verschoben wird. Da es sich um einen Random-Access-Iterator handelt, stehen die Chancen nicht schlecht, dass das Addieren eines Wertes, mit anschließendem wieder Abziehen, exakt wieder die Position erreicht, die der Iterator zuvor hatte. Das muss aber nicht zwingen so sein. betrachten wir das Ganze mal an einem Beispiel. Nehmen Sie an, sie hätten einen Iterator, der auf das letzte Element einer Sequenz zeigt. Wenn Sie mittels operator++() eins addieren, dann wird der Iterator auf das erste gedachte Element hinter der Sequenz zeigen und dieses ist das einzige Element, das zwingend nach der Sequenz existieren muss. Addieren Sie noch einmal eins, dann wird ein Random-Access-Iterator in den meisten Fällen auf ein zweites gedachtes Element hinter der gültigen Sequenz verweisen. Bei einem Bidirectional-Iterator wäre es hingegen sehr wahrscheinlich, dass er weiterhin auf das erste Element hinter der gültigen Sequenz zeigt. Wenn Sie also wieder eins abziehen, dann würde der Random-Access-Iterator anschließend wahrscheinlich auf das erste gedachte Element hinter der Sequenz zeigen. Wenn dem so ist, könnten wir eine solche Implementierung ins Auge fassen. Leider darf sich aber auch ein Random-Access-Iterator so verhalten, wie es ein Bidirectional-Iterator wahrscheinlich tun würde. Diese würde nämlich anschließend auf das letzte Element zeigen und bei einem derartigen Verhalten, wären wir plötzlich in der falschen Spalte. Da das Verhalten hier nicht sicher definiert ist, können wir diese Variante auch nicht guten Gewissens verwenden.

Wir speichern die Position stattdessen als ganzzahligen Wert, welchen wir bei einer angeforderten Dereferenzierung einfach zum Anfangsiterator des matrix-Objekt addieren. Auf dieses Weise ist sichergestellt, dass sich unser Iterator so verhält, wie es ein Random-Access-Iterator üblicherweise tun würde. Insbesondere ist aber auch sichergestellt, dass niemals versehentlich ein Objekt, aus einer anderen Spalte, referenziert werden kann, auch wenn unser Iterator zuvor schon einmal auf das erste Element hinter der Sequenz gezeigt hat, welches ja bezüglich den Matrixiteratoren auch mehrere Elemente hinter dessen letztem Element liegen kann. Hätten wir beispielsweise eine Matrix der Dimension 3, dann würden die Positionen, die für die zweite Spalte zwingend existieren müssen, bezüglich das Datenfeldes aus Matrix so aussehen:

123456789xxx Datenfeld
 ^  ^  ^  ^  Spalteniteratorpositionen

Wir benötigen für unsere Implementierung also einen Verweis auf das zugehörige matrix-Objekt und eine ganzzahlige Variable. Wie schon bei den Zeilenproxys werden wir diese beiden Datenmember gemeinsam mit den drei Konstruktoren, im protected-Bereich platzieren. Die ganzzahlige Variable wird vom Typ difference_type sein, da wir eine Entfernung ausdrücken wollen und bei einigen Berechnungen, innerhalb der Implementierung, können auch negative Werte entstehen. So etwa beim Subtrahieren zweier Iteratoren. Hierbei müssen intern die Positionen subtrahiert werden. Das matrix-Objekt kann entweder konstant oder nicht konstant sein, entsprechend werden wir dessen Typ als Templateparameter Matrix übergeben lassen. Der Member matrix_ ist dann vom Typ Matrix*, so dass der Zuweisungsoperator für die Klasse erzeugt werden kann. Außerdem benötigen wir für die typedefs wieder den passenden Iteratortyp der Matrixklasse. Diesen können wir leider nicht aus dem Templateparameter Matrix extrahieren, da der typedef iterator für matrix und matrix const immer noch identisch ist, wir benötigen für konstante Matrizen aber explizit matrix::const_iterator. Daher müssen wir uns auch diesen als Templateparameter übergeben lassen.

Für den Zugriff auf die Zeilenlänge werden wir uns eine Helfermethode im privaten Bereich anlegen, welche die Anzahl der Spalten aus dem matrix-Objekt zurückgibt. Da dies die Schrittweite für unsere Positionsvariable ist, werden wir die Methode step_width() nennen. Der Inkrement- bzw. Dekrement-Operator erhöht bzw. verringert unsere Positionsvariable um step_width(). Der operator+=() erhöht die Position um seinen Parameter mal step_width(). Der Gleichheitsoperator prüft, ob die Position und das matrix-Objekt übereinstimmen. Die Position wird hierbei zuerst geprüft, da es sehr wahrscheinlich ist, dass diese nicht übereinstimmt und dann muss die zweite Prüfung nicht mehr durchgeführt werden. Der Subtraktionsoperator für zwei Iteratoren bildet die Positionsdifferenz und teilt diese durch step_width(). Die Ganzzahldivision geht dabei immer genau auf. Der Indexoperator ruft den Plusoperator auf und gibt anschließend das dereferenziert Ergebnis zurück. Unsere Implementierung sieht somit wie Folgt aus:

template < typename Derived, typename Matrix, typename MatrixIterator >
class column_iterator_base:
    public random_access_iterator_base< Derived, typename MatrixIterator::difference_type >
{
public:
    typedef typename MatrixIterator::value_type      value_type;
    typedef typename MatrixIterator::difference_type difference_type;
    typedef typename MatrixIterator::pointer         pointer;
    typedef typename MatrixIterator::reference       reference;
    typedef std::random_access_iterator_tag          iterator_category;

    reference operator*()const{ return *(matrix_->begin() + pos_); }
    pointer operator->()const{ return matrix_->begin() + pos_; }

    Derived& operator++(){
        pos_ += step_width();
        return static_cast< Derived& >(*this);
    }
    Derived& operator--(){
        pos_ -= step_width();
        return static_cast< Derived& >(*this);
    }

    friend bool operator==(Derived const& lhs, Derived const& rhs){
        return lhs.pos_ == rhs.pos_ && lhs.matrix_ == rhs.matrix_;
    }

    Derived& operator+=(difference_type const& difference){
        pos_ += difference * step_width();
        return static_cast< Derived& >(*this);
    }

    friend difference_type const operator-(Derived const& lhs, Derived const& rhs){
        return (rhs.pos_ - lhs.pos_) / lhs.step_width();
    }

    reference operator[](difference_type const& index)const{
        return *(static_cast< Derived const& >(*this) + index);
    }

protected:
    column_iterator_base():
        matrix_(0), pos_(difference_type()){}

    column_iterator_base(Matrix& matrix, difference_type const& pos):
        matrix_(&matrix), pos_(pos){}

    column_iterator_base(column_iterator_base const& iter):
        matrix_(iter.matrix_), pos_(iter.pos_){}

    Matrix*         matrix_;
    difference_type pos_;

private:
    difference_type const step_width(){ return matrix_->columns(); }
};

Die Definition der abgeleiteten Proxyklassen ist komplett analog zu jener, die wir für die Iteratoren für konstante Matrizen vorgenommen haben.

template < typename Matrix >
class column_const_iterator:
    public column_iterator_base<
        column_const_iterator< Matrix >, Matrix const, typename Matrix::const_iterator
    >{
private:
    typedef column_iterator_base<
        column_const_iterator< Matrix >, Matrix const, typename Matrix::const_iterator
    > base;

public:
    column_const_iterator(){}
    column_const_iterator(Matrix const& matrix, typename base::difference_type const& pos):
        base(matrix, pos){}
};



template < typename Matrix >
class column_iterator:
    public column_iterator_base<
        column_iterator< Matrix >, Matrix, typename Matrix::iterator
    >{
private:
    typedef column_iterator_base<
        column_iterator< Matrix >, Matrix, typename Matrix::iterator
    > base;

public:
    column_iterator(){}
    column_iterator(Matrix& matrix, typename base::difference_type const& pos):
        base(matrix, pos){}

    operator column_const_iterator< Matrix >()const{
        return column_const_iterator< Matrix >(*this->matrix_, this->pos_);
    }
};

Schnittstellen der Proxyklassen

Jetzt müssen wir die Iteratorklassen nur noch in den Proxyklassen benutzten. Für alle vier Proxyklassen werden jetzt die typedefs iterator, const_iterator und difference_type eingeführt. Zum Erstellen von Iteratorobjekten gibt es jeweils die Methoden begin() und end(), die einen Iterator auf den Anfang, beziehungsweise hinter das Ende einer Sequenz erstellen. Die Berechnungen für konstante und nicht-konstante Matrizen sind immer identisch, die Methoden unterscheiden sich hier lediglich im Datentyp. Daher können wir diese wieder in einem entsprechenden Template zusammenfassen. Somit benötigen wir also vier Funktionstemplates zur Erstellung unserer Iteratorobjekte. Diese vier Funktionstemplates werden wir natürlich wieder im Namensraum detail deklarieren. Da sie zu den Proxyklassen gehören, stehen sie auch in der Datei proxy.hpp.

Die vier Funktionstemplates bekommen jeweils eine Referenz auf das matrix-Objekt und die Zeile bzw. Spalte, für die der jeweilige Iterator erstellt werden soll. Das matrix-Objekt kann konstant oder nicht-konstant sein. Der Iteratortyp muss entsprechend ein iterator oder const_iterator sein. Leider können wir den zu erstellenden Iteratortyp nicht vom Typ der Matrix ableiten, daher müssen wir beides als Templateparameter übergeben.

template < typename Matrix, typename Iterator >
inline Iterator const create_begin_row_iterator(
    Matrix& matrix, typename Matrix::size_type const& row
){
    return Iterator(matrix.begin() + (matrix.columns() * row));
}

template < typename Matrix, typename Iterator >
inline Iterator const create_end_row_iterator(
    Matrix& matrix, typename Matrix::size_type const& row
){
    return Iterator(matrix.begin() + (matrix.columns() * (row + 1)));
}


template < typename Matrix, typename Iterator >
inline Iterator const create_begin_column_iterator(
    Matrix& matrix, typename Matrix::size_type const& column
){
    return Iterator(matrix, column);
}

template < typename Matrix, typename Iterator >
inline Iterator const create_end_column_iterator(
    Matrix& matrix, typename Matrix::size_type const& column
){
    return Iterator(matrix, column + matrix.columns() * matrix.rows());
}

Die Iteratorinterfacemethoden sollen sich gegenseitig aufrufen, wenn Sie die gleiche Bedeutung haben. Nur wenn dies nicht der Fall ist, greifen wir auf die passende Funktionsinstanz des entsprechenden, eben definierten, Funktionstemplates zurück. Wie schon beim Iteratorinterface der Matrix, werden wir auch hier wieder konstante Iteratorobjekte zurückgeben um unsinnige Operationen explizit zu verbieten. Die Ergänzungen in den Proxyklassen sehen so aus:

template < typename Matrix >
class row_const_proxy: private detail::line_const_proxy< Matrix >{
public:
    typedef detail::row_const_iterator< matrix_type > const_iterator;
    typedef const_iterator                            iterator;
    typedef typename const_iterator::difference_type  difference_type;

    // ...

    const_iterator const begin()const{ return cbegin(); }
    const_iterator const end()const{ return cend(); }

    const_iterator const cbegin()const{
        return detail::create_begin_row_iterator< matrix_type const, const_iterator >(
            this->matrix_const(), pos()
        );
    }

    const_iterator const cend()const{
        return detail::create_end_row_iterator< matrix_type const, const_iterator >(
            this->matrix_const(), pos()
        );
    }
};

template < typename Matrix >
class column_const_proxy: private detail::line_const_proxy< Matrix >{
public:
    typedef detail::column_const_iterator< matrix_type > const_iterator;
    typedef const_iterator                               iterator;
    typedef typename const_iterator::difference_type     difference_type;

    // ...

    const_iterator const begin()const{ return cbegin(); }
    const_iterator const end()const{ return cend(); }

    const_iterator const cbegin()const{
        return detail::create_begin_column_iterator< matrix_type const, const_iterator >(
            this->matrix_const(), pos()
        );
    }

    const_iterator const cend()const{
        return detail::create_end_column_iterator< matrix_type const, const_iterator >(
            this->matrix_const(), pos()
        );
    }
};


template < typename Matrix >
class row_proxy: private detail::line_proxy< Matrix >{
public:
    typedef typename row_const_proxy< matrix_type >::const_iterator  const_iterator;
    typedef detail::row_iterator< matrix_type >                      iterator;
    typedef typename row_const_proxy< matrix_type >::difference_type difference_type;

    // ...

    iterator const begin()const{
        return detail::create_begin_row_iterator< matrix_type, iterator >(
            this->matrix(), pos()
        );
    }

    iterator const end()const{
        return detail::create_end_row_iterator< matrix_type, iterator >(
            this->matrix(), pos()
        );
    }

    const_iterator const cbegin()const{
        return detail::create_begin_row_iterator< matrix_type const, const_iterator >(
            this->matrix_const(), pos()
        );
    }

    const_iterator const cend()const{
        return detail::create_end_row_iterator< matrix_type const, const_iterator >(
            this->matrix_const(), pos()
        );
    }
};

template < typename Matrix >
class column_proxy: private detail::line_proxy< Matrix >{
public:
    typedef typename column_const_proxy< matrix_type >::const_iterator  const_iterator;
    typedef detail::column_iterator< matrix_type >                      iterator;
    typedef typename column_const_proxy< matrix_type >::difference_type difference_type;

    // ...

    iterator const begin()const{
        return detail::create_begin_column_iterator< matrix_type, iterator >(
            this->matrix(), pos()
        );
    }

    iterator const end()const{
        return detail::create_end_column_iterator< matrix_type, iterator >(
            this->matrix(), pos()
        );
    }

    const_iterator const cbegin()const{
        return detail::create_begin_column_iterator< matrix_type const, const_iterator >(
            this->matrix_const(), pos()
        );
    }

    const_iterator const cend()const{
        return detail::create_end_column_iterator< matrix_type const, const_iterator >(
            this->matrix_const(), pos()
        );
    }
};

Somit haben wir das Kapitel Proxyklassen abgeschlossen und verfügen über ein vollständiges Iteratorinterface für die gesamte Matrix, sowie deren Zeilen und deren Spalten. Als nächstes werden wir uns der Ein- und Ausgabe von Matrizen widmen. Auch hier werden wir wieder eine Ein- und Ausgabe für einzelne Zeilen uns Spalten anbieten und dabei von unseren Iteratorinterfaces Gebrauch machen.

Ein- und Ausgabe

	Dieses Kapitel ist leider noch nicht vorhanden…
	Wenn Sie Lust haben können Sie das Kapitel [[C++-Programmierung/ {{{Name}}}/ {{{Kapitel}}}|{{{Kapitel}}}]] selbst schreiben oder einen Beitrag dazu leisten.

Klassen für die Ausnahmebehandlung

	Dieses Kapitel ist leider noch nicht vorhanden…
	Wenn Sie Lust haben können Sie das Kapitel [[C++-Programmierung/ {{{Name}}}/ {{{Kapitel}}}|{{{Kapitel}}}]] selbst schreiben oder einen Beitrag dazu leisten.

Operationen

	Dieses Kapitel ist leider noch nicht vorhanden…
	Wenn Sie Lust haben können Sie das Kapitel [[C++-Programmierung/ {{{Name}}}/ {{{Kapitel}}}|{{{Kapitel}}}]] selbst schreiben oder einen Beitrag dazu leisten.

Verzögerte Berechnung

	Dieses Kapitel ist leider noch nicht vorhanden…
	Wenn Sie Lust haben können Sie das Kapitel [[C++-Programmierung/ {{{Name}}}/ {{{Kapitel}}}|{{{Kapitel}}}]] selbst schreiben oder einen Beitrag dazu leisten.

Zusammenfassung

	Zu diesem Abschnitt existiert leider noch keine Zusammenfassung…
	Wenn Sie Lust haben können Sie die [[C++-Programmierung/ {{{Name}}}/ Zusammenfassung|Zusammenfassung zum Abschnitt {{{Name}}}]] selbst schreiben oder einen Beitrag dazu leisten.