Einsteins Welt

Dieses Buch steht im Regal Physik.

Die Welt der Speziellen Relativitätstheorie

Fakten und Phänomene

Die Vakuum-Lichtgeschwindigkeit ist konstant

Grundlage der Speziellen Relativitätstheorie ist die Beobachtung, dass die Vakuum-Lichtgeschwindigkeit für jeden Beobachter denselben Wert hat – 299 792 km/s.

Auf den ersten Blick scheint diese Beobachtung völlig harmlos und unspektakulär zu sein, in Wirklichkeit gründet sich darauf die radikalste Umgestaltung des physikalischen Weltbildes mindestens seit Kopernikus. Und tatsächlich zeigt schon der zweite Blick auch dem physikalischen Laien, dass hier Ungeheuerliches behauptet wird, nämlich etwas, das dem so genannten gesunden Menschenverstand absurd erscheint.

Stellen wir uns vor, wir beobachteten eine Folge von Lichtimpulsen, die von links nach rechts über den Bildschirm laufen. Ferner bewege sich ein Raumschiff mit der Geschwindigkeit 200 000 km/s in derselben Richtung. Für uns neutrale Beobachter nähern sich die Lichtimpulse dem Raumschiff, das sich vor ihnen her bewegt, in jeder Sekunde um 100 000 km (also mit der Geschwindigkeit 100 000 km/s). Nachdem ein Lichtimpuls das Raumschiff überholt hat, entfernt er sich von ihm mit derselben Geschwindigkeit.

In der animierten Abbildung 1 (benutzen Sie zur Betrachtung bitte eine nicht zu antike Version des Internet Explorers) ist dies anschaulich dargestellt. Die Abbildung zeigt außerdem ein zweites Raumschiff, das sich mit gleicher Geschwindigkeit wie das erste, aber von rechts nach links bewegt, also den Lichtimpulsen entgegenläuft. Offenkundig nähern sich die Lichtimpulse diesem Raumschiff in jeder Sekunde um 500 000 km. Nach der Begegnung entfernen sie sich mit der gleichen Geschwindigkeit (500 000 km/s) von ihm.

Zur Veranschaulichung klicke auf Abb. 1: (bevorzugte Schrifteinstellung Ihres Browsers: Verdana, Schriftgrad: Sehr groß) Spezielle Relativitätstheorie

Diese beiden Beobachtungen sind auch in der Speziellen Relativitätstheorie nach wie vor richtig. Dagegen behauptet die Theorie – und sie wird darin durch unbezweifelbare Messergebnisse bestätigt – dass für einen Beobachter in jedem der beiden Raumschiffe die Geschwindigkeit der Lichtimpulse relativ zum jeweiligen Gefährt 300 000 km/s beträgt – nicht mehr und nicht weniger. Das heißt, die Lichtimpulse nähern sich dem Beobachter zunächst in jeder Sekunde um 300 000 km und entfernen sich nach der Überholung oder Begegnung genau so schnell von ihm.

Wie ist so etwas möglich? – Nun, für den „gesunden Menschenverstand“, das heißt hier: für unsere gängigen Vorstellungen (die sich auf Erfahrungen mit Geschwindigkeiten gründen, die sehr viel kleiner als die Lichtgeschwindigkeit sind), anders gesagt, für die klassische Newtonsche Mechanik, ist dieses Phänomen tatsächlich unmöglich. (Erstaunlich und wahrlich genial, dass Einstein nicht bereits hier die Flinte „Konstanz der Lichtgeschwindigkeit“ ins Korn geworfen hat.) Es ist nun also ein völliges Umdenken nötig, der schmerzliche Abschied von tief verwurzelten Vorstellungen, von als selbstverständlich geltenden Überzeugungen, die sich als naive Vorurteile erweisen werden. Denn es kommt alles noch viel, viel schlimmer. Wenn wir das Prinzip der Konstanz der Lichtgeschwindigkeit auf weitere Konsequenzen hin untersuchen, werden wir auf noch viel erstaunlichere Überraschungen treffen.

„Gleichzeitig“ ist relativ

Wieder machen wir ein einfaches Gedankenexperiment: Wir befinden uns auf einem sehr langen Bahnsteig (unserem „Bezugssystem“ S, siehe Abbildung 2). In zwei Punkten A und B, die sich links und rechts von uns in gleicher Entfernung (z. B. 300 m) befinden, schlagen gleichzeitig zwei Blitze ein. Die Gleichzeitigkeit dieser beiden Ereignisse können wir mit synchron gehenden Uhren in den Punkten A und B kontrollieren aber auch einfach daran erkennen, dass die Lichtsignale der beiden Blitze genau gleichzeitig bei uns eintreffen.

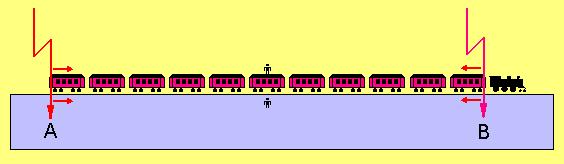
Abbildung 2: Ein auf dem Bahnsteig ruhender und ein mit dem Zug bewegter Beobachter beurteilen die „Gleichzeitigkeit“ zweier Ereignisse unterschiedlich.

Ferner nehmen wir an, ein sehr langer Zug bewege sich mit großer Geschwindigkeit auf dem Gleis neben dem Bahnsteig vorbei. Die beiden Blitze schlagen, bevor sie auf den Bahnsteig treffen, durch den Zug. Auf dem Dach des Zuges (dem Bezugssystem S’) stehe ebenfalls ein Beobachter, der sich im Moment des Blitzeinschlags gerade auf unserer Höhe befindet. Dieser Beobachter fährt mit dem Zug dem rechten Blitz entgegen und vor dem linken Blitz davon. Folglich wird das Lichtsignal von rechts ihn früher erreichen als das Lichtsignal von links. Da aber die Geschwindigkeiten der beiden Lichtsignale für den Beobachter – unabhängig von seiner Bewegung relativ zu uns – gleich sind, kommt der Beobachter zu dem Schluss, dass der rechte Blitz früher eingeschlagen hat als der linke.

Fazit: Zwei „gleichzeitige“ Ereignisse sind nur für Beobachter in demselben Bezugssystem tatsächlich gleichzeitig, nicht aber auch für Beobachter in einem Bezugssystem, das sich relativ zum ersten bewegt. Je nach der Bewegungsrichtung des zweiten Bezugssystems kann für einen Beobachter in diesem System das Ereignis in A vor oder auch nach dem Ereignis in B eingetreten sein.

Kritik am Beispiel: s. Diskussionsseite

Die Länge eines Körpers hängt von der Relativgeschwindigkeit des Beobachters ab

Die Länge eines Körpers zu messen ist eine simple Aufgabe, wenn der Körper relativ zu dem Beobachter ruht, der die Messung ausführt. Anders sieht es aus, wenn die Länge eines Körpers bestimmt werden soll, der sich am Beobachter vorbeibewegt. Jetzt kommt es darauf an, dass die Position des Anfangs- und die des Endpunktes genau gleichzeitig auf einem Maßstab markiert wird.

Abbildung 3: Messung der Länge des Zuges, der sich von links nach rechts bewegt, durch Beobachter am Bahnsteig.

1. Die Position der Spitze des Zuges und die des Zug-Endes werden gleichzeitig markiert (rot).Zuglänge: l₀

2. Die Position des Zug-Endes wird später markiert als die Position des Zug-Anfangs (grün). So ergibt sich für die Zuglänge der zu kleine Wert l.

Was aber, wenn zwischen einem Beobachter, der mit dem Körper mitreist, und dem anderen, der den vorüberbewegten Körper ausmessen will, Uneinigkeit darüber besteht, was „gleichzeitig“ ist? Dann werden die beiden Beobachter zu unterschiedlichen Ergebnissen kommen, und zwar wird – wie sich zeigen lässt – der Beobachter, an dem sich der Körper vorbeibewegt, stets einen kleineren Wert ermitteln als der andere. Der Grund dafür ist nicht das Messverfahren (man könnte die Messung auch photographisch vornehmen), sondern die Relativität der Gleichzeitigkeit, die wiederum auf der Konstanz der Lichtgeschwindigkeit beruht.

Dazu ein beliebtes Beispiel:

Durch einen Carport von 8 m Länge fliegt eine Rakete von 10 m „Ruhelänge“ (das ist die Länge, wie sie vor dem Start oder von einem mit der Rakete fliegenden Beobachter gemessen wurde).

Frage: Bei welcher Geschwindigkeit passt die Rakete unter das Dach des Carports, sodass zu irgendeinem Zeitpunkt weder vorn noch hinten etwas von ihr übersteht?

Aus der einschlägigen Formel kann man berechnen, dass die Rakete vollständig unter das Carport passt, wenn sie mit einer Geschwindigkeit von mindestens 240 000 km/s fliegt.

Dauer ist nicht gleich Dauer (Das „Zwillingsparadoxon“)

Max und Moritz sind Zwillingsbrüder sehr unterschiedlichen Charakters. Max liebt die Beständigkeit und bleibt am liebsten immer zu Hause. Moritz dagegen ist reise- und abenteuerlustig. So bucht er eines Tages eine längere Reise auf einem sehr schnellen Raumschiff. Nach 8 Jahren Reisezeit (gemessen mit den Präzisionsuhren im Raumschiff) kehrt er nach Hause zurück und stellt fest, dass sein Bruder Max inzwischen um 10 Jahre gealtert ist und dass auf der Erde insgesamt seit dem Start des Raumschiffs 10 Jahre vergangen sind.

Das Paradoxe an diesem Paradoxon besteht allerdings darin, dass der fortreisende Moritz in der Anfangsphase seiner Reise beim Blick zurück die Zeit für seinen daheim gebliebenen Bruder langsamer verstreichen sieht, aus seiner Sicht also - vorerst - Max jünger bleibt. Das löst sich allerdings auf, denn Moritz kann seinen Heimatplaneten nicht erreichen ohne zu beschleunigen! Und wenn er sich wieder auf seine Heimat zu bewegt sieht er Max umso schneller altern. Dieses Phänomen lässt sich aber nur zum Teil mit dem Dopplereffekt erklären; der andere Teil entstammt der Zeitdilatation, die mit Moritz' Beschleunigung entsteht. Wenn die Brüder einander wieder treffen, so ist für beide wieder die gleiche Situation hergestellt: Max ist älter als Moritz.

Dieses Phänomen lässt sich mathematisch beweisen und auch experimentell bestätigen (zum Beispiel an µ-Mesonen, die in der oberen Atmosphäre entstehen und manchmal in Richtung Erdoberfläche auf die Reise gehen, deren Lebensdauer aber an sich nicht ausreicht, um die Erdoberfläche zu erreichen, das jedoch trotzdem tun). Aber es lässt sich nicht ohne weiteres plausibel machen und „begreifen“. Dies ist nur möglich – und dann sogar recht einfach – aus der Struktur der Welt Einsteins heraus, die so ganz anders ist als die Struktur der Welt Newtons.

Problem: In der SRT geht es nicht um Beschleunigungen, sondern um Inertialsysteme. Einstein hat selbst gesagt (mit der Aufklärung dieses Paradoxons in der ART), daß der Altersunterschied nur durch die Beschleunigung des "Reisenden" hervorgerufen wird und nicht durch die Geschwindigkeit, die er zuvor hatte.

Energie ist träge, und Masse ist „eingefrorene“ Energie

Dieses Phänomen nennt man auch – nicht ganz korrekt –, die „Äquivalenz von Masse und Energie“. Streng genommen geht es darum, dass Energie – gleich welcher Art – genau wie eine Masse Trägheit besitzt und dass umgekehrt aus Masse Energie entstehen kann. Konkret bedeutet das, dass bei Erwärmung des Wassers in einem Teekessel seine Masse zunimmt, es also sowohl träger als auch schwerer wird. Ferner: Aus Energie können körperliche Teilchen entstehen („Paarerzeugung“) und körperliche Teilchen können zu Energie „zerstrahlt“ werden. Bei allen Prozessen, bei denen Wärme oder andere Formen von Energie entstehen, verschwindet ein (meist sehr kleiner) Teil der beteiligten Masse. Dies ist der Fall bei allen Verbrennungsvorgängen und bei der Spaltung schwerer Atomkerne sowie bei der Verschmelzung leichter Atomkerne zu schwereren Kernen. Masse m und Energie E sind jedoch nicht gleich, sondern proportional, wobei das Quadrat der Lichtgeschwindigkeit c der Proportionalitätsfaktor ist:

$E=m\cdot c^{2}$

Die Trägheit der Energie ist auch die Ursache dafür, dass die Masse eines Körpers mit der Geschwindigkeit (relativ zu einem Beobachter) zuzunehmen scheint. Der tatsächliche Grund für die Zunahme der Trägheit mit der Geschwindigkeit ist jedoch die Trägheit der kinetischen Energie, die der Körper besitzt. Die Vorstellung der »relativistischen Massenzunahme« oder »Relativität der Masse« wird unter Physikern mehr und mehr aufgegeben zugunsten der (beweisbaren) Annahme, dass die Masse eine immanente, vom Bezugssystem unabhängige Größe ist, genau wie die elektrische Ladung.

Die Struktur der Welt

Newtons Welt (die Welt des „gesunden Menschenverstandes“)

Wir haben wiederholt festgestellt: die von der Speziellen Relativitätstheorie beschriebenen Phänomene – einschließlich der Konstanz der Lichtgeschwindigkeit – seien letztlich nur aus einer neuen Sicht der Struktur der Welt zu verstehen, genauer: aus einer neuen Sicht der Struktur des Raumes und des Wesens der Zeit. Sie sind ganz und gar unverständlich, ja geradezu absurd in der Welt, wie Newton und nach ihm die klassische Physik sie verstand.

Newtons Welt bestand im Prinzip aus einem „absoluten“, dreidimensionalen euklidischen Raum und einer darin ablaufenden „absoluten“ Zeit. Über beide schrieb Newton:

Der absolute Raum bleibt vermöge seiner Natur und ohne Beziehung auf einen äußeren Gegenstand stets gleich und unbeweglich.

Die absolute, wahre und mathematische Zeit verfließt an sich und vermöge ihrer Natur gleichförmig und ohne Beziehung auf irgendeinen äußeren Gegenstand. (Philosophiae naturalis principia mathematica, 1687)

Ein euklidischer Raum ist ein Raum, in dem die Gesetze gelten, wie sie von der Euklidischen Geometrie beschrieben werden. Zwei davon sollen als Beispiele genannt werden:

Die Summe der Winkel eines (ebenen) Dreiecks beträgt 180°.

Das Quadrat über der Diagonale d eines Quaders ist gleich der Summe der Quadrate über seiner Länge a, seiner Breite b und seiner Höhe c:

a² + b² + c² = d²

Letzteres ist die räumliche Version des Lehrsatzes von Pythagoras.

Die Welt nach Einstein

Die Welt, in der die Gesetze gelten und die Phänomene auftreten, wie sie von der Speziellen Relativitätstheorie beschrieben werden, hat folgende Merkmale:

1. Der Raum hat vier Dimensionen. Drei davon bilden den euklidischen Raum, wie wir ihn täglich erfahren. Nennen wir ihn unseren Erfahrungsraum E₃. Er ist identisch mit dem absoluten Raum Newtons.

2. Der Erfahrungsraum E₃ bewegt sich mit Lichtgeschwindigkeit c in Richtung der vierten Dimension des Raumes der Speziellen Relativitätstheorie.

3. Die vierte Dimension ist – genau wie die drei Dimensionen des Erfahrungsraumes – von der Art „Länge“ (einer eindimensionalen räumlichen Ausdehnung), und nicht, wie Minkowski und seine Schüler geglaubt haben bzw. noch immer glauben, von der Art „Zeit“.

4. Während der Erfahrungsraum, wie oben gesagt, euklidisch ist, bildet die vierte Dimension zusammen mit diesem euklidischen Raum einen vierdimensionalen Raum von einer anderen Struktur, die als „pseudoeuklidisch“ bezeichnet wird. Aus dieser pseudoeuklidischen Struktur ergeben sich zwanglos und notwendig alle von der Speziellen Relativitätstheorie beschriebenen Phänomene. Anders gesagt: In diesem Raum können sich physikalische Vorgänge gar nicht anders abspielen, als die Spezielle Relativitätstheorie es beschreibt; Körper und Uhren können sich in diesem Raum gar nicht anders verhalten, ihr Verhalten ist gleichsam das natürliche und einzig mögliche.

5. Die oben beschriebene Bewegung des Erfahrungsraumes in Richtung der vierten Dimension ist für uns natürlich nicht vorstellbar, weil unsere Wahrnehmung und unser Vorstellungsvermögen von Natur aus auf drei Dimensionen beschränkt sind. Statt dieser Bewegung registrieren wir etwas, das wir den Ablauf der Zeit nennen. Anders gesagt: Alle Veränderungen in unserem Erfahrungsraum, die wir mit dem Ablauf der Zeit in Verbindung setzen (und ohne Veränderungen gäbe es keine Zeit), hängen in Wirklichkeit mit der Bewegung des Erfahrungsraumes in Richtung der vierten räumlichen Dimension zusammen.

Diese Gedankengänge sind in einem Aufsatz des Autors genauer ausgeführt, der auf http://home.vrweb.de/~si.pe/Wesen%20der%20Zeit/Wesen.htm zu finden ist.

Wie gesagt, ist es uns unmöglich, uns einen vierdimensionalen Raum vorzustellen. Daher müssen wir, wenn wir uns näher damit beschäftigen wollen, auf eine der drei Dimensionen unseres Erfahrungsraumes (zum Beispiel die Höhe) verzichten. Wir stellen uns also vor, wir lebten in einer zweidimensionalen Welt („Flachland“), in der es nur Länge und Breite, aber keine Höhe gibt. Der Erfahrungsraum ist also eine Ebene (die XY-Ebene) und alle „Körper“ in ihm sind zweidimensional, flach. Dann können wir die dritte Dimension – die Höhe – zur Darstellung der vierten Dimension W benutzen. Das sieht dann so aus:

Abbildung 4: Ein zweidimensionaler (ebener) Zug, der in einem zweidimensionalen Erfahrungsraum ruht.

Man stelle sich nun vor, dass sich die XY-Ebene und mit ihr der Zug mit Lichtgeschwindigkeit nach oben (in Richtung der W-Achse) bewegt.

Als nächstes stellen wir uns vor, der Zug bewege sich relativ zur XY-Ebene mit großer Geschwindigkeit v nach rechts. Er stellt nun ein relativ zum Bezugssystem S (das ist die XY-Ebene) bewegtes Bezugssystem S’ dar. Wir erweitern dieses Bezugssystem zu einer mit dem Zug bewegten X’Y’-Ebene.

Wie die Spezielle Relativitätstheorie zeigt, werden durch die Bewegung des Bezugssystems die X’-Achse und die W’-Achse um einen bestimmten Winkel α nach links (also gegen den Uhrzeigersinn) gedreht, der von der Geschwindigkeit v abhängt. Die Y’-Achse fällt weiterhin mit der Y-Achse zusammen, und die W’-Achse steht weiterhin auf der X’-Achse senkrecht.

Doch nun gibt es eine Schwierigkeit. Die XW-Ebene und die X’W’-Ebenen sind pseudoeuklidische Ebenen, also Ebenen mit einer anderen „Metrik“ als unsere Zeichenebene (das ist hier die Bildschirmebene). Die Eigenarten und Gesetze der pseudoeuklidischen Ebene aber lassen sich nicht ohne weiteres in einer euklidischen Ebene darstellen. Das macht sich dann deutlich und störend bemerkbar, wenn wir das zweite, gedrehte X’W’-Koordinatensystem gleichzeitig zusammen mit dem XW-Koordinatensystem abbilden wollen. (Und zwar stimmen dann die von der Theorie ermittelten Zusammenhänge zwischen den X- und W-Koordinaten eines Punktes einerseits und seinen X’- und W’-Koordinaten andererseits nicht mehr.) Zum Glück lässt sich diese Schwierigkeit beheben, wenn wir dafür eine kleine Komplikation in Kauf nehmen. Diese besteht darin, dass das X’W’-Koordinatensystem nicht mehr rechtwinklig (und gedreht), sondern schiefwinklig abgebildet wird. (Außerdem müssen die Einheitsstrecken auf den Achsen in bestimmter Weise verändert werden, was uns hier aber nicht weiter interessiert.) Dann sieht der bewegte Zug zusammen mit seinem und dem anderen Bezugssystem so aus:

Abbildung 5: Ein bewegter Zug in seinem Bezugssystem zur Zeit t’ = 0

Wie oben gesagt wurde, bewegt sich der Erfahrungsraum (hier die XY-Ebene) mit Lichtgeschwindigkeit in Richtung der W-Achse. Der Nullpunkt der X-Achse und der Y-Achse gleitet dabei auf der W-Achse nach oben. (Der Nullpunkt der W-Achse bleibt dabei unverändert.) Entsprechendes gilt auch für den bewegten Erfahrungsraum (die X’Y’-Ebene): Der Nullpunkt der X’Y’-Ebene bewegt sich mit Lichtgeschwindigkeit auf der W’-Achse nach oben. Die nächste Abbildung zeigt eine Anzahl von Momentaufnahmen des bewegten Zuges, der sich mit seiner X’Y’-Ebene nach oben bewegt, und zwar auch für Zeiten t’ < 0. (Die XY-Ebene ist dabei nur für t = 0 abgebildet.)

Abbildung 6: Die Lage des Zuges in der X’Y’-Ebene zu verschiedenen Zeiten t’. (t’ ist die im Bezugssystem S’ geltende Zeit, die sich von t unterscheidet.)

Ein Beobachter in der XY-Ebene nimmt in seinem Erfahrungsraum (das ist die XY-Ebene) natürlich den ganzen Zug wahr. Aber: In verschiedenen Punkten (einige davon sind grün hervorgehoben) der X-Achse beobachtet er Teile des Zuges, die aus ganz verschiedenen Ebenen stammen und damit aus ganz verschiedenen Zeiten t’. Lediglich im Nullpunkt der X-Achse wird ein Punkt des Zuges beobachtet, für den t’ = 0 ist; für alle anderen gezeichneten Punkte ist t’ < 0.

Wenn aber die verschiedenen Punkte des Zuges vom Beobachter in S gleichzeitig wahrgenommen werden können, dann müssen sie dort auch existieren. Das bedeutet aber, dass der bewegte Zug nicht nur in einer einzigen Lage existiert, sondern gleichzeitig überall vorhanden ist. Der von uns als eben (das heißt: zweidimensional) angesehene Zug ist also in Wirklichkeit ein räumliches (das heißt: dreidimensionales) Gebilde, von dem ein Beobachter in S – genau so wie ein Beobachter in S’ – nur jeweils einen ebenen Ausschnitt wahrnimmt.

Auf unseren dreidimensionalen Erfahrungsraum übertragen bedeutet das: Alle Gegenstände (einschließlich unseres eigenen Körpers) sind in Wirklichkeit vierdimensionale Gebilde, von denen wir jeweils nur einen dreidimensionalen Ausschnitt wahrnehmen. Der Grund dafür ist, dass unser Vorstellungsvermögen und unser Bewusstsein auf drei Dimensionen beschränkt sind und wir zeitlich nacheinander wahrnehmen, was in Wirklichkeit gleichzeitig im vierdimensionalen Raum vorhanden ist. Unsere „vergangenen“ Wahrnehmungen liegen also im vierdimensionalen Raum „unterhalb“ unseres Erfahrungsraumes, die künftigen Wahrnehmungen liegen „oberhalb“ dessen, wobei sich „unterhalb“ und „oberhalb“ auf die Lage in der vierten Dimension beziehen.

Erinnern wir uns, dass sich unser dreidimensionaler Erfahrungsraum mit Lichtgeschwindigkeit in Richtung der vierten Dimension bewegt. Genau genommen bewegt sich nur der momentan von uns wahrgenommene Ausschnitt aus der vierdimensionalen Wirklichkeit so. Man kann also sagen, dass sich lediglich unser Bewusstsein und das, was es momentan wahrnimmt, mit Lichtgeschwindigkeit durch die vierdimensionale Realität bewegen. Weil unser Bewusstsein nur dreidimensionale Körper wahrnehmen kann, ist ihm die vierdimensionale Realität nicht zugänglich. Dafür betrachtet es sich zeitlich nacheinander dreidimensionale Schichten der Realität, die in Wirklichkeit über einander angeordnet sind. Es wandert gleichsam wie der Besucher einer Gemäldeausstellung von Bild zu Bild und betrachtet sich nacheinander, was in Wirklichkeit gleichzeitig an verschiedenen Orten anwesend ist.

Aus dieser Sicht sind die Relativitäten der Länge und der Gleichzeitigkeit unmittelbar verständlich. Dass in dieser so ganz anderen Welt die Energie träge ist und zwei Personen unterschiedlich altern können, erschließt sich allerdings nicht direkt der Anschauung, sondern nur einer mathematischen Durchdringung.