Formelsammlung Chemie/ Berechnung des pH-Wertes
Vernachlässigt man die konzentrations- und ladungsabhängigen Aktivitätskoeffizienten der bei ihrer Dissoziation freigesetzten und einander beeinflussenden Anionen und Kationen, kann der pH-Wert einer in Wasser gelösten Säure oder Base näherungsweise über die Konzentration an Oxoniumionen [H3O+] der betreffenden Lösung berechnet werden.
Eine exakte Berechnung dagegen ist meist wesentlich aufwändiger, wenn nicht gar gänzlich unmöglich. Dennoch sind für verschiedene Standardfälle brauchbare Näherungsformeln entwickelt worden, die im folgenden vorgestellt werden, wobei stets berücksichtigt werden sollte, dass diese Formeln strenggenommen nur für bestimmte Konzentrationsbereiche und/oder pKA/pKB-Werte ausgelegt sind und auch, was „stark“, „mittelstark“ oder „schwach“ genannt wird, sich von Quelle zu Quelle bzw. Autor zu Autor unterscheiden kann.
Weitgehende Übereinstimmung dagegen besteht darin, dass man die Näherungsformeln grob danach unterteilen kann, ob die betreffende Säure bzw. Base in wässriger Lösung als praktisch vollständig dissoziiert bzw. protoniert angenommen wird oder aber außer ihrer Ausgangskonzentration c0 auch noch ihre Säure-Konstante KA bzw. Basen-Konstante KB eine Rolle spielt.
Ausgehend davon werden auch im nachfolgenden Text die verschiedenen Näherungsformeln nach ihrer jeweiligen Ausgangssituation geordnet sowie abschließend in einer Übersichtstabelle für diejenigen, die lediglich die Formeln selbst suchen, zusammengefasst.
Einprotonige Systeme
[Bearbeiten]Stark dissoziierte Säuren
[Bearbeiten]Traditionell „stark“ genannte Säuren mit pKA-Werten um -2 und darunter sind schon in hoher Konzentration in wässriger Lösung praktisch vollständig deprotoniert bzw. dissoziiert, Säuren mit höheren pKA-Werten dagegen erst bei stärkerer Verdünnung.
Als Richtwert, ab wann von „starker“ Dissoziation gesprochen werden kann, gilt dabei eine mindestens 99%-ige Dissoziation beziehungsweise die Bedingung:
Ist sie erfüllt, gilt damit für eine solche Lösung näherungsweise folgende Ladungsbilanz:
Stellt man diese Gleichung nach der Oxoniumionen-Konzentration [H3O+] um, ergibt sich die nachstehende, per p/q-Formel lösbare quadratische Gleichung:
- .
Ausgehend davon findet sich als allgemeine Lösung dieser Gleichung die Formel
in der, wie man sieht, über das Ionenprodukt des Wassers KW auch die aus der Autoprotolyse des Lösungsmittels Wasser stammenden Ionen mit in die Berechnung einfließen.
Ist die Säure nicht allzu stark verdünnt (Ausgangskonzentration c0 > 10-6 mol/l [1]) und das Ionenprodukt des Wassers KW damit dem Ausdruck (c0/2)² gegenüber vernachlässigbar klein, kann og. Gleichung in sehr guter Näherung zu folgender noch einfacheren Formel verkürzt werden:
Setzt man die so erhaltene Oxoniumionen-Konzentration [H3O+] anstelle ihrer Aktivität in die Definitionsgleichung des pH-Werts, ergibt sich dieser wie folgt:
Beispiel: pH-Wert einer 0,1 M Salzsäure
Achtung: Die in diesem Abschnitt vorgestellten Näherungsformeln für „stark“ dissoziierte Säuren gelten damit ausdrücklich nicht nur für sogen. „starke“ Säuren mit entsprechend niedrigen pKA-Werten, sondern auch für entsprechend stark verdünnte „mittelstarke“ und „schwache“ Säuren - Kriterium der Anwendbarkeit og. Formeln ist allein die eingangs aufgestellte Beziehung zwischen c0 und KA!
Mittelstark dissoziierte Säuren
[Bearbeiten]Anders als bei traditionell „stark“ genannten Säuren mit pKA-Werten um -2 oder darunter, die selbst in vergleichsweise hoher Konzentration noch praktisch vollständig dissoziiert bzw. deprotoniert sind, liegt das Dissoziationsgleichgewicht in wässrigen Lösungen „mittelstarker“ Säuren nicht mehr überwiegend auf Seiten der dissoziierten, aber auch noch nicht wieder vorwiegend auf Seiten der undissoziierten Form.
Für HA als die undissoziierte Säure kann dieses Gleichgewicht dann gemäß MWG durch folgende Gleichung mit KA als zugehöriger Säurekonstante beschrieben werden:
Soll daraus die aktuelle Oxoniumionen-Konzentration [H3O+] berechnet werden, ergibt sich unter Einbeziehung der Ladungsbilanz zunächst einmal die nachstehende, allenfalls mittels der cardanischen Formeln exakt lösbare Gleichung dritten Grades
beziehungsweise
- .
Ist das Produkt KA⋅KW gegenüber den vorausgehenden Termen vernachlässigbar klein, die Lösung also nicht allzu stark verdünnt, lässt diese Gleichung sich jedoch auf die wesentlich einfachere, weil per p/q-Formel lösbare quadratische Gleichung
reduzieren, deren allgemeine Lösung
die Oxoniumionen-Konzentration [H3O+] in Abhängigkeit von der Ausgangskonzentration c0 sowie den beiden Konstanten KA und KW liefert. Als Richtwert einer nicht allzu starken Verdünnung gilt dabei eine Konzentration von
Achtung: Da diese Näherungsformel die Säurekonstante KA mit berücksichtigt, kann sie als allgemeinste der drei hier vorgestellten Näherungsformeln für einprotonige Säuren - solange das Kriterium nicht allzu starker Verdünnung erfüllt bleibt! - gleichgut auch für „stärkere“ und „schwächere“ Säuren eingesetzt werden!
Ist die betreffende Säure dagegen stärker verdünnt, gewinnt das zuvor vernachlässigte Produkt KA⋅KW zunehmend an Bedeutung, so dass auch die Oxoniumionen-Konzentration gemäß obiger Näherungsformel mit zunehmendem KA tendenziell zu tief ausfällt, sich also für c0 = 0 nicht mehr der Neutralwert von 10-7 mol/l einstellt.
Ist schließlich auch noch das Ionenprodukt des Wassers KW gegenüber dem Produkt KA⋅c0 vernachlässigbar klein (wovon man ab einem Verhältnis von KA⋅c0 ≥ 100⋅KW = 10-12 mol²/l² ausgeht), vereinfacht sich die obige Formel noch einmal weiter zu:
Beispiel: pH-Wert einer 0,1 M Dichloressigsäure (pKA = 1,3)
Schwach dissoziierte Säuren
[Bearbeiten]So wie das Dissoziationsgleichgewicht bei traditionell „stark“ genannten Säuren selbst in vergleichsweise hoher Konzentration noch praktisch vollständig auf Seiten ihrer dissoziierten bzw. deprotonierten Form liegt, liegt es umgekehrt bei traditionell „schwach“ genannten Säuren mit pKA-Werten über 4,5 selbst in vergleichweise niedriger Konzentration noch vorwiegend auf Seiten ihrer undissoziierten bzw. protonierten Form, bei Säuren mit niedrigeren pKA-Werten dagegen erst ab höherer Konzentration.
Als Richtwert, bis wohin von „schwacher“ Dissoziation gesprochen werden kann und damit nachfolgend vorgestellte Näherungsformel Anwendung findet, gilt eine höchstens 1%-ige Dissoziation, wie sie im Fall nachstehender Bedingungen angenommen wird:
Gelten sie (oder auch nur eine von beiden), vereinfacht sich die og. Formel für „mittelstarke“ Säuren dadurch, dass nun der Ausdruck KA/2 als vernachlässigbar klein gegenüber KA⋅c0 ignoriert wird, noch einmal weiter zu der Näherung
wobei es auch hier üblich ist, die aus der Autoprotolyse des Wassers stammenden Ionen bei nicht allzu starker Verdünnung zu ignorieren:[2]
Setzt man die so erhaltene Oxoniumionen-Konzentration [H3O+] anstelle ihrer Aktivität in die Definitionsgleichung des pH-Werts, ergibt sich dieser wie folgt:
Beispiel: pH-Wert einer 0,1 M Ammoniumchlorid-Lösung (pKA = 9,244}
Stark protonierte Basen
[Bearbeiten]In Umkehrung dessen, was eingangs zu „stark“ genannten Säuren gesagt wurde, können „starke“ Basen mit pKB-Werten ≤ 0, z. B. Hydroxylionen, auch schon in hoher Konzentration in wässriger Lösung als praktisch vollständig protoniert, d.h. „undissoziiert“ betrachtet werden, Basen mit höheren pKB-Werten dagegen erst bei stärkerer Verdünnung.
Als Richtwert, ab wann von „starker“ Protonierung gesprochen werden kann, gilt dabei eine mindestens 99%-ige Protonierung beziehungsweise die Bedingung:
Ist sie erfüllt, ergibt sich für eine solche Lösung - wieder über die Ladungsbilanz - zunächst einmal folgende allgemeine Näherungslösung:
Beispiel: pH-Wert einer 10-8 M Kalilauge
Ein limitierender Faktor kann dabei allerdings z. B. die Löslichkeit des betreffenden Hydroxids sein, etwa bei Erdalkalihydroxiden wie Calcium- oder Magnesiumhydroxid, die zwar kraft ihrer Hydroxylionen gleichfalls zu den „starken“ Basen gezählt werden müssen, aufgrund ihrer Schwerlöslichkeit und damit niedrigen Maximalkonzentration jedoch nur eine schwache Basenwirkung entfalten, verbunden mit dementsprechend niedrigen pH-Werten.
Ist die Base hingegen nicht allzu stark verdünnt und das Ionenprodukt des Wassers KW damit dem Ausdruck (c0/2)² gegenüber vernachlässigbar klein (was ab Ausgangskonzentrationen c0 von ca. 2⋅10-6 mol/l der Fall ist), kann og. Gleichung in sehr guter Näherung weiter zu folgender noch einfacheren Formel verkürzt werden:
Setzt man die so erhaltene Oxoniumionen-Konzentration [H3O+] anstelle ihrer Aktivität in die Definitionsgleichung des pH-Werts, ergibt sich dieser nun wie folgt:
Achtung: Die in diesem Abschnitt vorgestellten Näherungsformeln für „stark“ protonierte Basen gelten damit ausdrücklich nicht nur für sogen. „starke“ Basen mit entsprechend niedrigen pKB-Werten, sondern auch für entsprechend stark verdünnte „mittelstarke“ und „schwache“ Basen - Kriterium der Anwendbarkeit og. Formeln ist allein die eingangs aufgestellte Beziehung zwischen c0 und KB!
Mittelstark protonierte Basen
[Bearbeiten]Anders als bei „stark“ genannten Basen mit pKB-Werten um 0 oder darunter, die selbst in vergleichsweise hoher Konzentration noch praktisch vollständig protoniert sind, liegt das Protolysegleichgewicht in wässrigen Lösungen „mittelstarker“ Basen nicht mehr überwiegend auf Seiten der protonierten, aber auch noch nicht wieder vorwiegend auf Seiten der deprotonierten Form.
Bezeichnet B dabei die deprotonierte Base, wird dieses Gleichgewicht gemäß MWG durch die folgende Gleichung mit KB als zugehöriger Basenkonstante beschrieben:
Soll daraus die aktuelle Hydroxidionen-Konzentration [OH-] berechnet werden, ergibt sich unter Einbeziehung der Ladungsbilanz auch hier eine nicht ohne weiteres lösbare Gleichung dritten Grades
- ,
die sich, falls das Produkt KB⋅KW gegenüber den vorausgehenden Termen vernachlässigbar klein, die Lösung also nicht allzu stark verdünnt ist, auf die wesentlich einfachere, weil per p/q-Formel lösbare quadratische Gleichung
reduzieren lässt und - analog der obigen - die allgemeine Lösung
beziehungsweise
liefert. Als Richtwert einer nicht allzu starken Verdünnung gilt dabei wiederum eine Konzentration von
Achtung: Da diese Näherungsformel die Basenkonstante KB mit berücksichtigt, kann sie als allgemeinste der drei hier vorgestellten Näherungsformeln für einprotonige Basen - solange das Kriterium nicht allzu starker Verdünnung erfüllt bleibt! - gleichgut auch für „stärkere“ und „schwächere“ Basen eingesetzt werden!
Ist die betreffende Base hingegen stärker verdünnt, gewinnt das zuvor vernachlässigte Produkt KB⋅KW zunehmend an Bedeutung, so dass auch die Oxoniumionen-Konzentration gemäß obiger Näherungsformel mit zunehmendem KB tendenziell zu hoch ausfällt, sich also für c0 = 0 nicht mehr der Neutralwert von 10-7 mol/l einstellt.
Ist schließlich auch noch das Ionenprodukt des Wassers KW gegenüber dem Produkt KB⋅c0 vernachlässigbar klein (wovon man ab einem Verhältnis von KB⋅c0 ≥ 100⋅KW = 10-12 mol²/l² ausgeht), vereinfacht sich obige Formel noch einmal weiter zu:
Schwach protonierte Basen
[Bearbeiten]So wie das Protolysegleichgewicht bei traditionell „stark“ genannten Basen selbst in vergleichsweise hoher Konzentration noch praktisch vollständig auf Seiten ihrer protonierten Form liegt, liegt es umgekehrt bei traditionell „schwach“ genannten Basen mit pKB-Werten über 4,5 selbst in vergleichweise niedriger Konzentration noch vorwiegend auf Seiten ihrer deprotonierten Form, bei Basen mit niedrigeren pKB-Werten dagegen erst ab höherer Konzentration.
Als Richtwert, bis wohin von „schwacher“ Protonierung geprochen werden kann und damit die nachfolgend vorgestellte Näherungsformel Anwendung findet, gilt dabei eine höchstens 1%-ige Protonierung, wie sie im Fall nachstehender Bedingungen angenommen wird:
Gelten sie (oder auch nur eine von beiden), vereinfacht sich die og. Formel für „mittelstarke“ Basen dadurch, dass der Ausdruck KB/2 nun als vernachlässigbar klein gegenüber KB⋅c0 ignoriert wird, noch einmal weiter zu der Näherung
wobei es auch hier üblich ist, die aus der Autoprotolyse des Wassers stammenden Ionen bei nicht allzu starker Verdünnung zu ignorieren:
Beispiel: pH-Wert einer 0,5 M Kaliumcyanid-Lösung (pKB = 4,6)
Setzt man die so erhaltene Oxoniumionen-Konzentration [H3O+] anstelle ihrer Aktivität in die Definitionsgleichung des pH-Werts, ergibt sich dieser wie folgt:
Beispiel: pH-Wert einer 1,0 M Natriumchlorit-Lösung (pKB = 12,05)
Die Näherungsformeln im Vergleich
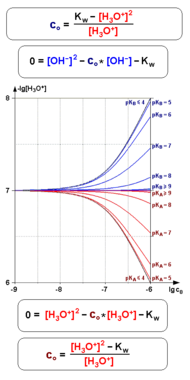
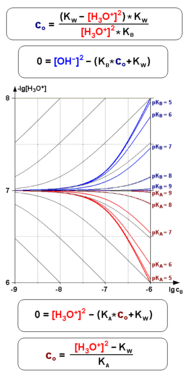
[Bearbeiten]Die nachstehenden Grafiken geben einen Überblick über die Abhängigkeit der Oxoniumionen-Konzentration [H30+] einprotoniger Säuren und Basen von ihrer Ausgangskonzentration c0 und der jeweiligen Säure- bzw. Basenkonstante, zum einen berechnet nach den exakten kubischen Gleichungen (ganz links), zum anderen nach den drei bislang vorgestellten Näherungformeln für „starke“, „mittelstarke“ sowie „schwache“ Säuren und Basen. Wie zu sehen, liefern dabei die Formeln für „mittelstarke“ Säuren und Basen (2. v.r.) die mit Abstand beste Übereinstimmung mit den von den exakten Formeln erbrachten Zahlenwerten, allerdings nur für nicht allzu starke Verdünnungen mit Ausgangskonzentrationen c0 ≥ 10-6 mol/l:
Darunter dagegen liefern allenfalls die beiden Näherungsformeln für „starke“ Säuren bzw. Basen (2. v.l.) bei pK-Werten ≤ 4 sowie für „schwache“ Säuren bzw. Basen (ganz rechts) bei pK-Werten ≥ 8 brauchbare Resultate - für Säuren und Basen mit pK-Werten zwischen 4 und 8 sowie einer Ausgangskonzentration c0 < 10-6 mol/l hingegen exisitieren, wie sich zeigt, einstweilen keine verlässlichen Näherungsformeln:
Zweiprotonige Systeme
[Bearbeiten]Anders als bei den bisher diskutierten einprotonigen Säuren der allgemeinen Formel HA, die in wässriger Lösung lediglich in dieser „Säureform“ HA sowie als korrespondierende Base A- vorkommen, gibt es für zweiprotonige Säuren der allgemeinen Formel H2A gleich drei in wässriger Lösung miteinander im Gleichgewicht stehende Formen: besagte „Säureform“ H2A sowie außerdem die „Ampholyt-“ oder „Intermediatform“ HA- und schließlich die „Basenform“ A2-, mit der Folge, dass nun statt einer Säurekonstante KA zwei solche Konstanten, KA1 und KA2 genannt, in die pH-Wert-Berechnung einfließen.
Saure Form H2A
[Bearbeiten]Soll die Oxoniumionen-Konzentration [H3O+] einer in Wasser gelösten zweiprotonigen Säure H2A mittlerer Stärke exakt, d. h. unter Einbeziehung aller sich dabei einstellenden Gleichgewichte bestimmt werden, läuft dies - ausgehend von der Ladungsbilanz - auf die Lösung nachfolgender nichtrivialen Gleichung vierten Grades hinaus:
Für die meisten Anwendungsfälle jedoch ist es hinreichend, die Säure - eine nicht allzu starke Verdünnung vorausgesetzt - wie eine mittelstarke einprotonige Säure mit KA = KA1 zu behandeln und ihre Oxoniumionen-Konzentration gemäß folgender Näherungsformel zu berechnen:
Wie sich zeigen lässt, liefert diese Vorgehensweise selbst für nahe beieinander liegende Säurekonstanten KA1 und KA2 noch brauchbare Näherungswerte. So ergibt sich selbst für den Fall KA1 = 10·KA2 lediglich ein Fehler von ΔpH = 0,01[3], was angesichts der Genauigkeit gängiger pH-Meter für praktische Zwecke völlig ausreichend ist.
In den meisten Fällen nämlich kommt es durch die Vernachlässigung der Aktivitätskoeffizienten (s.o.) sowie andere Ungenauigkeiten wie die Abhängigkeit der verwendeten Konstanten von Temperatur, Ionenstärke usw. zu wesentlich größeren Abweichungen, weshalb man die berechneten pH-Werte in der Praxis nur als Richtwert verwenden, d. h. anschließend stets noch einmal nachmessen sollte.
Beispiel: pH-Wert einer 0,1 M Oxalsäure (pKA1 = 1,252)
Wird auch die in dieser Rechnung unberücksichtigt gebliebene zweite Dissoziationsstufe mit einbezogen, ergibt sich der annähernd gleiche, weil erst in der vierten Nachkommastelle abweichende Wert von .
Analog kann eine nicht allzu stark verdünnte mittelstarke zweiwertige Base in erster Näherung wie eine einwertige Base mit KB = KB1 behandelt werden.
Ampholyt- oder Intermediatform HA-
[Bearbeiten]Bringt man die Ampholyt- oder Intermediatform einer zweiprotonigen Säure mittlerer Stärke, z. B. ihr Natriumsalz NaHA, in Lösung, kann diese ähnlich wie es Pufferlösungen oder Zwitterionen, z.B. Aminosäuren, tun, sowohl Protonen abgeben wie Protonen binden, d.h. sowohl als Säure wie als Base reagieren.
Stoffe, die dies vermögen, werden Säure-Base-Amphotere oder Ampholyte genannt, und so stehen auch in diesem Fall drei verschiedene Formen derselben Säure miteinander im Gleichgewicht: die „Säureform“ H2A, die „Intermediatform“ HA- und die „Basenform“ A2-.
Soll die Oxoniumionen-Konzentration [H3O+] einer solchen Lösung exakt, d. h. unter Einbeziehung aller sich einstellenden Gleichgewichte bestimmt werden, läuft dies - ausgehend von der Ladungs- und Stoffmengenbilanz - auf die Lösung nachfolgender nichtrivialen Gleichung vierten Grades hinaus:
Liegen die beiden pKA-Werte hinreichend weit auseinander, dominiert die Intermediatform HA- allerdings so sehr, dass ihre Gleichgewichtskonzentration [HA-] näherungsweise der Ausgangskonzentration c0 gleichgesetzt werden kann, was eine erhebliche Vereinfachung der Berechnung mit sich bringt und - wieder vorausgesetzt, die Ausgangskonzentration c0 ist weder zu hoch noch zu niedrig - zu folgender Näherungsformel für die Oxoniumionen-Konzentration führt:
Beispiel: pH-Wert einer 0,01 M Glycin-Lösung (pKA1 = 2,350, pKA2 = 9,778)
Anmerkung: Dass im Fall des Glycins die Intermediatform [HA] ungeladen, die vollständig protonierte „Säureform“ [H2A+] dagegen einfach positiv und die vollständig deprotonierte „Basenform“ [A-] einfach negativ geladen ist, spielt für die Berechnung keine Rolle. Eine genaue Bestimmung der Konzentrationen der drei Formen bei og. pH-Wert ([H2A+] = 1,6·10-6 mol/l, [HA] = 9,996·10-3 mol/l, [A-] = 2,3·10-6 mol/l) bestätigt im übrigen, dass die näherungsweise Gleichsetzung der Ausgangs- und Gleichgewichtskonzentration der Intermediatform in diesem Beispiel vollauf gerechtfertigt ist.
Sind sowohl KA1 gegenüber c0 als auch KW gegenüber KA2· c0 vernachlässigbar klein, vereinfacht sich diese Formel noch einmal weiter zu der zumal im Schulunterricht verbreiteten sogen. „Ampholytgleichung“, in der der pH-Wert eines Ampholyts sich als konzentrationsunabhängiger Mittelwert seiner beiden Säurekonstanten darstellt:
Eine weitere, ebenfalls verbreitete Schreibweise dieser stark vereinfachten Näherungsformel schließlich verwendet anstelle der zweiten Säurekonstante die korrespondierende Basenkonstante, was zu folgenden, ebenfalls häufig anzutreffenden Formeln führt:
Achtung: Da der pH-Wert in diesen Fällen unabhängig von der Ausgangskonzentration c0 der Intermediatform HA- – selbst für den Grenzfall c0→0! – stets derselbe bleibt, kann diese Formel nur als sehr grobe Näherung für nicht allzu stark verdünnte Lösungen (c0 ≥ 0,1 mol/l) von Ampholyten dienen, deren Säurekonstanten dazu außerdem, wie bereits eingangs gesagt, hinreichend weit auseinander liegen sollten!
Basische Form A2-
[Bearbeiten]Analog dazu, dass zweiprotonige Säuren bei der Berechnung des pH-Werts ihrer „Säureform“ H2A in erster Näherung wie einprotonige Säuren behandelt werden können, kann man auch die „Basenform“ zweiprotoniger Säuren A2- rechnerisch als quasi einwertige Basen mit KB = KB2 behandeln. Für den pH-Wert einer nicht allzu stark verdünnten mittelstarken zweiwertigen Base A2- gilt dann näherungsweise:
Beispiel: pH-Wert einer 0,1 M Natriumsulfit-Lösung (pKB2 = 6,82)
Gemischte Systeme
[Bearbeiten]Werden zwei verschiedene Säuren oder eine (schwache) Säure mit einem ihrer Salze gemischt, gibt es für die Oxoniumionen-Konzentrationen der resultierenden Mischungen eine Reihe weiterer Näherungsformeln.
Zwei schwache Säuren
[Bearbeiten]Für die Mischung zweier einprotoniger schwacher Säuren mit hinreichend weit auseinander liegenden pKA-Werten und außerdem nicht allzu großer Verdünnung gilt näherungsweise:
Eine schwache und eine starke Säure
[Bearbeiten]Ist dagegen nur die erste der beiden Säuren schwach, die zweite dagegen stark, gilt unter den genannten Randbedingungen näherungsweise:
Beispiel: pH-Wert einer 2/3 M Essigsäure (pKA1 = 4,76) und 1/300 M HCl
Eine schwache Säure und ihr Salz
[Bearbeiten]Mischt man die nicht allzu stark verdünnte Lösung des Salzes einer einprotonigen schwachen Säure (z.B. Natriumacetat) mit dieser Säure selbst oder einer starken Säure (die einen Teil der eingesetzten Anionen zur undissoziierten Säure HA protoniert), kann die Oxoniumionen-Konzentration der resultierenden Mischung (und damit deren pH-Wert) mit Hilfe der sogen. Puffer– oder Henderson-Hasselbalch-Gleichung geschätzt werden:
Begrenzt wird die Einsetzbarkeit dieser Formel dabei allerdings durch die zusätzliche Forderung, dass das Konzentrationsverhältnis von Säure zu Salz [HA]/[A-] im Bereich zwischen 1:10 und 10:1 liegen sollte, da sie außerhalb dieses Bereichs schnell ihre Gültigkeit verliert.
Gültigkeitsgrenzen der vorgestellten Näherungsformeln
[Bearbeiten]Gemeinsamer Ausgangspunkt aller vorstehend diskutierten Näherungsformeln ist die Gültigkeit des Massenwirkungsgesetzes, also namentlich die bei seiner kinetischen Ableitung gemachte „Voraussetzung einer ungestörten regellosen Bewegung der Moleküle“[4], die jedoch in Elektrolytlösungen schon ab relativ niedrigen Konzentrationen nicht mehr gegeben ist.
So erreichen die Ionenkonzentrationen bei schwachen Elektrolyten bereits ab einer Konzentration von ca. 0,1 mol/l, bei mittelstarken ab ca. 0,01 mol/l und bei starken schon ab 0,001 mol/l Werte, bei denen og. Voraussetzung „infolge der gegenseitigen Anziehung der Ionen [...] nicht mehr zutrifft ('reale Lösungen')“ und die Anziehungskräfte der Ionen sich nach außen hin so auswirken, „als wäre die Konzentration der Ionen geringer, als sie es in Wirklichkeit ist.“ [4]
Um das MWG gleichwohl auch auf solche Situationen anwenden zu können, muss – wenn man es genau nehmen will - jede Ionenkonzentration ci noch einmal mit einem von der Gesamtionenstärke als auch der Konzentration und Ladung des betreffenden Ions selbst abhängigen Aktivitätskoeffizienten fi multipliziert werden, um so statt mit der stöchiometrischen Konzentration ci mit der tatsächlich wirksamen „effektiven“ Ionenkonzentrationen fi·ci rechnen zu können, aus der sich schließlich durch Entdimensionalisierung die dimensionslose Aktivität ai des betreffenden Ions i ergibt.
Das gilt auch – und im Zusammenhang dieses Artikels insbesondere - für den pH-Wert, der exakterweise nicht als negativer dekadischer Logarithmus der Oxoniumionen-Konzentration, sondern Oxoniumionen-Aktivität definiert ist.[5][6]
Bis zu welcher Grenze man den pH-Wert gleichwohl ohne größeren Fehler aus der Oxoniumionen-Konzentration berechnen darf, wird dabei in der Literatur unterschiedlich und zum Teil widersprüchlich angegeben. So erlauben etwa die Chemischen Tabellen und Rechentafeln für die analytische Praxis, sofern „die Lösung - bezogen auf die Gesamtkonzentration an Elektrolyten - nicht stärker als 0,1 n ist“, „für praktische Zwecke“ eine Gleichsetzung der Oxoniumionen-Konzentration mit der Oxoniumionen-Aktivität,[6] während dieselbe Quelle, wenn es genauer sein soll, die Grenze, bis zu der man die Zahlenwerte von Aktivität und Konzentration gleichsetzen darf, schon bei einer Ionenstärke von I ≤ 0,0001 mol/l zieht. [7]
Für alle höher konzentrierten Säuren bzw. Basen dagegen muss strengenommen stets das Debye-Hückel-Grenzgesetz herangezogen werden, mit dem sich aus der Konzentration einer Elektrolytlösung die Aktivitätskoeffizienten fi ihrer einzelnen Ionen berechnen lassen.[7][8]
Zusammenfassung
[Bearbeiten]| Gültig für | Bedingungen | Oxoniumionen-Konzentration |
|---|---|---|
| Stark dissoziierte Säuren [9] | c0 ≤ KA/102 | |
| dto., vereinfacht [9][10] | dto., KW ≪ (c0/2)² |
|
| Mittelstark dissoziierte Säuren | c0 ≥ 10-6 mol/l | |
| dto., vereinfacht [9][10] | dto., KW ≪ KA⋅c0 |
|
| Schwach dissoziierte Säuren | c0 ≥ KA⋅104 oder KA ≤ 10-8 mol/l |
|
| dto., vereinfacht [9] | dto., KW ≪ KA⋅c0 |
|
| Eine schwache (1) und eine starke (2) Säure, vereinfacht [9][10] |
- | |
| Zwei schwache Säuren, vereinfacht [10] | - | |
| Eine schwache Säure und ihr Salz, vereinfacht [9][10] | - | mit |
| Ampholyte | - | |
| dto., vereinfacht [9][10] | c0 ≫ KA1, KA2⋅c0 ≫ KW |
|
| dto., vereinfacht | c0 ≪ KA1 | |
| Schwach protonierte Basen | c0 ≥ KB⋅104 oder KB ≤ 10-8 mol/l |
|
| dto., vereinfacht | dto., KW ≪ KB⋅c0 |
|
| Mittelstark protonierte Basen | c0 ≥ 10-6 mol/l | |
| dto., vereinfacht | dto., KW ≪ KB⋅c0 |
|
| Stark protonierte Basen [9] | c0 ≤ KB/102 | |
| dto., vereinfacht [9][10] | dto., KW ≪ (c0/2)² |
Weblinks
[Bearbeiten]Einzelnachweise
[Bearbeiten]- ↑ Gary D. Christian: Analytical Chemistry - 6th Ed., John Wiley & Sons Inc. (2004)
- ↑ Jander/Jahr: Maßanalyse, 15. Auflage, de Gruyter, Berlin 1989, S. 83-90.
- ↑ Daniel C. Harris: Lehrbuch der quantitativen Analyse, Vieweg (1997)
- ↑ 4,0 4,1 Hollemann/Wiberg: Lehrbuch der Anorganischen Chemie; Berlin 1956, S.107.
- ↑ Lothar Kolditz [Hrsg.]: Anorganikum. Lehr- und Praktikumsbuch der anorganischen Chemie mit einer Einführung in die physikalische Chemie; Berlin 1970, S. 297.
- ↑ 6,0 6,1 K.Rauscher, J.Voigt, I.Wilke, K.-Th.Wilke: Chemische Tabellen und Rechentafeln für die analytische Praxis; Leipzig 1968, S.144.
- ↑ 7,0 7,1 K.Rauscher, J.Voigt, I.Wilke, K.-Th.Wilke: Chemische Tabellen und Rechentafeln für die analytische Praxis; Leipzig 1968, S.146.
- ↑ Lothar Kolditz [Hrsg.]: Anorganikum. Lehr- und Praktikumsbuch der anorganischen Chemie mit einer Einführung in die physikalische Chemie; Berlin 1970, S. 192, 326, 420.
- ↑ 9,0 9,1 9,2 9,3 9,4 9,5 9,6 9,7 9,8 Nesper, Reinhard Friedrich. Skript zur Vorlesung Allgemeine Chemie I. Text: Säuren und Basen. ETH Zürich, Laboratorium für Anorganische Chemie (2001), S.46-58.
- ↑ 10,0 10,1 10,2 10,3 10,4 10,5 10,6 Nesper, Reinhard Friedrich. Skript zur Vorlesung Allgemeine Chemie I. Folie 3: Säuren und Basen. ETH Zürich, Laboratorium für Anorganische Chemie (2001), S.13-23.


![{\displaystyle \mathrm {\ [H_{3}O^{+}]=[A^{-}]+[OH^{-}]\approx c_{0}+[OH^{-}]=c_{0}+K_{W}/[H_{3}O^{+}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d66dd23b7d765ba90dee7ebe466171701519fbc)
![{\displaystyle \ \mathrm {[H_{3}O^{+}]^{2}-c_{0}\cdot [H_{3}O^{+}]-K_{W}=0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/35976879b69d50c5e2031b834281277dac026c37)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{W}+\left({\frac {c_{0}}{2}}\right)^{2}}}+{\frac {c_{0}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d153ca46421da033168403b289195d4dbe439a3)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {{\xcancel {K_{W}\ +}}\ \left({\frac {c_{0}}{2}}\right)^{2}}}+{\frac {c_{0}}{2}}\ =\ c_{0}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/38786388e4dfe6f9dc81a7716acc28d86003b5f8)
![{\displaystyle \mathrm {\!\ pH\approx -\log _{10}[H_{3}O^{+}]=-\log _{10}\left(c_{0}\cdot {\frac {l}{mol}}\right)} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/91d37b1f7ad4c91cb517ff390688877cadf1f1e9)
![{\displaystyle \mathrm {\ [H_{3}O^{+}]=c_{0}=0{,}1\ mol/l\quad \Rightarrow \quad pH\approx 1} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/87ec638f4337a1e67a167a308cb806d39406f5b9)
![{\displaystyle \mathrm {K_{A}={\frac {[H_{3}O^{+}]\cdot [A^{-}]}{[HA]}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10bc60d5a79e28534f8407fedbfac0eee00b6ef)
![{\displaystyle \mathrm {[H_{3}O^{+}]-{\frac {K_{A}\cdot c_{0}}{[H_{3}O^{+}]+K_{A}}}-{\frac {K_{W}}{[H_{3}O^{+}]}}=0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a0cf75bec69ce31030a18f7adf9b6aeaf8e692c)
![{\displaystyle \mathrm {[H_{3}O^{+}]^{3}+K_{A}\cdot [H_{3}O^{+}]^{2}-(K_{A}\cdot c_{0}+K_{W})\cdot [H_{3}O^{+}]-K_{A}\cdot K_{W}=0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3ee5d1e03caf3c14ad172a672e13027a420c28)
![{\displaystyle \mathrm {[H_{3}O^{+}]^{2}+K_{A}\cdot [H_{3}O^{+}]-(K_{A}\cdot c_{0}+K_{W})=0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed80d7f4a7831012fe0b3f49c8aa3f2da8c9e223)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{W}+K_{A}\cdot c_{0}+\left({\frac {K_{A}}{2}}\right)^{2}}}-{\frac {K_{A}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1497e20c5868fb4b1cf075d9f3f34864118a5ee)

![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {{\xcancel {K_{W}\ +}}\ K_{A}\cdot c_{0}+\left({\frac {K_{A}}{2}}\right)^{2}}}-{\frac {K_{A}}{2}}\ =\ {\sqrt {K_{A}\cdot c_{0}+\left({\frac {K_{A}}{2}}\right)^{2}}}-{\frac {K_{A}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a587c269f2bd441b75cf6d4e78322141747fd7c)
![{\displaystyle \mathrm {[H_{3}O^{+}]={\sqrt {10^{-1{,}3}\ M\cdot 0{,}1\ M+\left({\frac {10^{-1{,}3}\ M}{2}}\right)^{2}}}-{\frac {10^{-1{,}3}\ M}{2}}\quad \Rightarrow \quad pH\approx 1{,}3} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7126b89f70cacbb27d133cdf087d4459a397729)

![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{W}+K_{A}\cdot c_{0}\ {\xcancel {+\left({\frac {K_{A}}{2}}\right)^{2}}}}}\;\;{\xcancel {-{\frac {K_{A}}{2}}}}\ =\ {\sqrt {K_{W}+K_{A}\cdot c_{0}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/07f7256d90b6b77f502fb3be7998ee59c09bb8f0)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {{\xcancel {K_{W}+}}\ K_{A}\cdot c_{0}\ }}={\sqrt {K_{A}\cdot c_{0}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d66dc317edad1ddbf74b7433dced7805337cc72c)
![{\displaystyle \mathrm {pH\approx {\frac {1}{2}}\left[pK_{A}-log_{10}\left(c_{0}\cdot {\frac {l}{mol}}\right)\right]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/92b08bbfea07a7492bd547c11b4802dff38bd078)
![{\displaystyle \mathrm {pH\approx {\frac {1}{2}}\left[9{,}244-log_{10}\left(0{,}1\right)\right]=5{,}12} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/11d8b70ba5ebb71e6bae917a4974488f3cc6e381)

![{\displaystyle \mathrm {\ [H_{3}O^{+}]=K_{W}\ /\ [OH^{-}]\ \approx \ K_{W}\ /\ \left({\sqrt {K_{W}+\left({\frac {c_{0}}{2}}\right)^{2}}}+{\frac {c_{0}}{2}}\right)={\sqrt {K_{W}+\left({\frac {c_{0}}{2}}\right)^{2}}}-{\frac {c_{0}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/faf1aeaff4050355879f37a7dd8305a372883141)
![{\displaystyle \mathrm {[H_{3}O^{+}]={\sqrt {10^{-14}\ M^{2}+\left({\frac {10^{-8}\ M}{2}}\right)^{2}}}-{\frac {10^{-8}\ M}{2}}\quad \Rightarrow \quad pH\approx 7{,}02} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/21b191d510632dd7d47a8a459e082b6431b8f351)
![{\displaystyle \mathrm {\ [H_{3}O^{+}]=K_{W}\ /\ [OH^{-}]\ \approx \ K_{W}\ /\ ({\sqrt {{\xcancel {K_{W}\ +}}\ \left({\frac {c_{0}}{2}}\right)^{2}}}+{\frac {c_{0}}{2}})\ =\ K_{W}/c_{0}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/502e0dd9e154dd17ed00f5f75ab0f80b790cbfe2)

![{\displaystyle \mathrm {K_{B}={\frac {[BH^{+}]\cdot [OH^{-}]}{[B]}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/be620f93fb5f369629fdd77370a183e6b990411c)
![{\displaystyle \mathrm {[OH^{-}]^{3}+K_{B}\cdot [OH^{-}]^{2}-(K_{B}\cdot c_{0}+K_{W})\cdot [OH^{-}]-K_{B}\cdot K_{W}=0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/30049e057af675215d228bea55928ad39704077d)
![{\displaystyle \mathrm {[OH^{-}]^{2}+K_{B}\cdot [OH^{-}]-(K_{B}\cdot c_{0}+K_{W})=0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8101fcb7e755970682c090162a96af5fbd7e4503)
![{\displaystyle \mathrm {[OH^{-}]\approx {\sqrt {K_{W}+K_{B}\cdot c_{0}+\left({\frac {K_{B}}{2}}\right)^{2}}}-{\frac {K_{B}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/28ab9ccdfc6dd1f900a03c9c3e74dc0fc25fb8d7)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}\ /\ \left({\sqrt {K_{W}+K_{B}\cdot c_{0}+\left({\frac {K_{B}}{2}}\right)^{2}}}-{\frac {K_{B}}{2}}\right)} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/71d6c7f33fbdba579227182e4d54701093c7d0dd)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}/\left({\sqrt {{\xcancel {K_{W}\ +}}\ K_{B}\cdot c_{0}\ +\left({\frac {K_{B}}{2}}\right)^{2}}}-{\frac {K_{B}}{2}}\right)=K_{W}/\left({\sqrt {K_{B}\cdot c_{0}+\left({\frac {K_{B}}{2}}\right)^{2}}}-{\frac {K_{B}}{2}}\right)} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e954905e920c79bdb4a20abcc5888654cbd6c8fb)

![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}/({\sqrt {K_{W}+K_{B}\cdot c_{0}\ {\xcancel {+\left({\frac {K_{B}}{2}}\right)^{2}}}}}\;\;{\xcancel {-{\frac {K_{B}}{2}}}})\ =\ K_{W}/{\sqrt {K_{W}+K_{B}\cdot c_{0}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/133b1964d47cfaa829e74fef2ee03c93895fd456)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}/{\sqrt {{\xcancel {K_{W}+}}\ K_{B}\cdot c_{0}\ }}\ =\ K_{W}/{\sqrt {K_{B}\cdot c_{0}}}={\sqrt {\frac {K_{W}\cdot K_{A}}{c_{0}}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2665b8af30e06936480b8d025f1045ee56b30f6c)
![{\displaystyle \mathrm {[H_{3}O^{+}]=10^{-14}\ M^{2}\ /\ {\sqrt {10^{-4{,}6}\ M\cdot 0{,}5\ M}}\quad \Rightarrow \quad pH\approx 11{,}55} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f3320fa99ef44c641466f20de6343f48798050f)
![{\displaystyle \mathrm {pH\approx 14-{\frac {1}{2}}\left[pK_{B}-log_{10}\left(c_{0}\cdot {\frac {l}{mol}}\right)\right]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a0ddbd9a816bb254f9ab21cc5e4ae92fafbae96)
![{\displaystyle \mathrm {pH\approx 14-{\frac {1}{2}}\left[12{,}05-log_{10}\left(1{,}0\right)\right]=7{,}98} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/52b18e2c4d6d3ce9bad056edff86555378399b1e)






![{\displaystyle \mathrm {[H_{3}O^{+}]-c_{0}\cdot {\frac {K_{A1}\cdot [H_{3}O^{+}]+2\cdot K_{A1}\cdot K_{A2}}{[H_{3}O^{+}]^{2}+K_{A1}\cdot [H_{3}O^{+}]+K_{A1}\cdot K_{A2}}}-{\frac {K_{W}}{[H_{3}O^{+}]}}=0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a375d76e770d5e4ec5cfaa7922a790d0bcda5938)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{A1}\cdot c_{0}+\left({\frac {K_{A1}}{2}}\right)^{2}}}-{\frac {K_{A1}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab26101bb6b5bf833cfbec1c253a6c3730f92394)
![{\displaystyle \mathrm {[H_{3}O^{+}]={\sqrt {10^{-1{,}252}\ M\cdot 0{,}1\ M+\left({\frac {10^{-1{,}252}\ M}{2}}\right)^{2}}}-{\frac {10^{-1{,}252}\ M}{2}}\quad \Rightarrow \quad pH\approx 1{,}28_{49}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1ec4dfec75d908fc8f4bc1d913520541e39971c)

![{\displaystyle \mathrm {[H_{3}O^{+}]+c_{0}\cdot {\frac {[H_{3}O^{+}]^{2}-K_{A1}\cdot K_{A2}}{[H_{3}O^{+}]^{2}+K_{A1}\cdot [H_{3}O^{+}]+K_{A1}\cdot K_{A2}}}-{\frac {K_{W}}{[H_{3}O^{+}]}}=0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/950742d8bed91f9511f7bca955b0f2ab55e6b0af)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {\frac {K_{A1}\cdot (K_{A2}\cdot c_{0}+K_{W})}{K_{A1}+c_{0}}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/19356d011856815757a7d14ddd3b2ac08dfeef44)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {\frac {10^{-2{,}350}\ M\cdot (10^{-9{,}778}\ M\cdot 0{,}01\ M+10^{-14}\ M^{2})}{10^{-2{,}350}\ M+0{,}01\ M}}}\quad \Rightarrow \quad pH\approx 6{,}14} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf733ce5eb9b203f1e62823333448b1c8cc43dbf)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {\frac {K_{A1}\cdot (K_{A2}\cdot c_{0}\ {\xcancel {+\ K_{W}}})}{{\xcancel {K_{A1}\ +}}\ c_{0}}}}={\sqrt {K_{A1}\cdot K_{A2}}}\quad \Rightarrow \quad pH\approx {\frac {1}{2}}\left(pK_{A1}+pK_{A2}\right)} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1949a9e4e897ca28cd4e75b95cf10f4a561c4453)

![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}\ /\ ({\sqrt {K_{B2}\cdot c_{0}+({\frac {K_{B2}}{2}})^{2}}}-{\frac {K_{B2}}{2}})} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab1b2393610917b2c879d3fe05ee9e5b21d0b04d)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}\ /\ ({\sqrt {10^{-6{,}82}\ M\cdot 0{,}1\ M+\left({\frac {10^{-6{,}82}\ M}{2}}\right)^{2}}}-{\frac {10^{-6{,}82}\ M}{2}})\quad \Rightarrow \quad pH\approx 10{,}09} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae3e173fabfaac0a97b0281c2af2603ca3fdef3d)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {c_{0_{\text{Säure1}}}\cdot K_{\text{Säure1}}+c_{0_{\text{Säure2}}}\cdot K_{\text{Säure2}}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7872a1e662470661a3af79458cd7c4b2a850db0)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {c_{0_{\text{Säure1}}}\cdot K_{\text{Säure1}}+\left({\frac {c_{0_{\text{Säure2}}}}{2}}\right)^{2}}}+{\frac {c_{0_{\text{Säure2}}}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f00401d58224ac6e4a752bc098df61df563755a)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {2/3\ M\cdot 10^{-4{,}76}\ M+\left({\frac {1\ M}{600}}\right)^{2}}}+{\frac {1\ M}{600}}\quad \Rightarrow \quad pH\approx 2{,}26} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/781cf41dba2b898e7ce8e0f0e706e3ece8ceba8b)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{A}\cdot {\frac {[HA]}{[A^{-}]}}\quad \Rightarrow \quad pH\approx pK_{A}-log_{10}\left({\frac {[HA]}{[A^{-}]}}\right)} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/90a0b1ec62ceddea4b2e6f98c6548bb81b394c21)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{W}+\left({\frac {c_{0}}{2}}\right)^{2}}}\ +{\frac {c_{0}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a7c579ffeb7bb7d92fcb05c4351a2b5b4f4f442)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {{\xcancel {K_{W}+}}\ \left({\frac {c_{0}}{2}}\right)^{2}}}\ +{\frac {c_{0}}{2}}\ =\ c_{0}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/884a3811651eca4a78d6f70dd190bf0f5a5a2247)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{W}+K_{A}\cdot c_{0}+({\frac {K_{A}}{2}})^{2}}}\ -{\frac {K_{A}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b3702f961d0597c56b96b373338322e7f0e249a)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{A}\cdot c_{0}+\left({\frac {K_{A}}{2}}\right)^{2}}}\ -{\frac {K_{A}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/220c08757af8bbb3435946432b393d8771428235)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{W}+K_{A}\cdot c_{0}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/de1ba99cdac052ca5058553f318f57ba11ead9ce)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{A}\cdot c_{0}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/db72a8c10337e97358febf83d5a5dfe5fb721f93)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{A1}\cdot c_{0_{1}}+\left({\frac {c_{0_{2}}}{2}}\right)^{2}}}+{\frac {c_{0_{2}}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/61c3e9e394c4c253df9339bd6678548fbb315109)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {K_{A1}\cdot c_{0_{1}}+K_{A2}\cdot c_{0_{2}}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9e2b0a8764e81a9c51edac34d106ace6f6115be)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{A}\cdot {\frac {[HA]}{[A^{-}]}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c6482b91b85e204e069c18a474ed9a98b1a20ca)
![{\displaystyle 0{,}1<{\frac {[HA]}{[A^{-}]}}<10}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2ca59c86138a5d8b62db10722b4f296d07e657f)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {\frac {K_{A1}\cdot (K_{A2}\cdot c_{0}\ {\xcancel {+K_{W}}})}{{\xcancel {K_{A1}+}}\ c_{0}}}}\approx {\sqrt {K_{A1}\cdot K_{A2}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1bf7deba675bb8912f328ba529c7651b09979c9)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx {\sqrt {\frac {K_{A1}\cdot (K_{A2}\cdot c_{0}+K_{W})}{K_{A1}\ {\xcancel {+c_{0}}}}}}\approx {\sqrt {K_{A2}\cdot c_{0}+K_{W}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/988aea3cba296924754f32eaebe4a7088e4f4ed7)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}/{\sqrt {K_{W}+K_{B}\cdot c_{0}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b92d977707d42d3bb03bce115f721ac36db7f17)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}/{\sqrt {K_{B}\cdot c_{0}}}={\sqrt {\frac {K_{W}\cdot K_{A}}{c_{0}}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b54bbc99597532e38ebcf6ad27d675c1592d2122)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}/\left({\sqrt {K_{W}+K_{B}\cdot c_{0}+\left({\frac {K_{B}}{2}}\right)^{2}}}-{\frac {K_{B}}{2}}\right)} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e56dfc7e3febd13b3d553be6879e9461f7c8ee1)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}/\left({\sqrt {K_{B}\cdot c_{0}+\left({\frac {K_{B}}{2}}\right)^{2}}}-{\frac {K_{B}}{2}}\right)} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/85b55fcd096556741d76996edabbaa8d66ad9f54)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}/\left({\sqrt {K_{W}+\left({\frac {c_{0}}{2}}\right)^{2}}}+{\frac {c_{0}}{2}}\right)={\sqrt {K_{W}+\left({\frac {c_{0}}{2}}\right)^{2}}}-{\frac {c_{0}}{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3652602acc4d56b3fc3f57f673c59cbd966ff5bd)
![{\displaystyle \mathrm {[H_{3}O^{+}]\approx K_{W}/\left({\sqrt {{\xcancel {K_{W}+}}\ \left({\frac {c_{0}}{2}}\right)^{2}}}+{\frac {c_{0}}{2}}\right)\ =\ {\frac {K_{W}}{c_{0}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/91e55b678dc6344f523c88555c5dc0c27994f7d6)