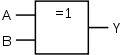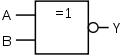Umrechnung Dezimalzahlen in andere Zahlensysteme [ Bearbeiten ] Umwandlung Dual - Dezimal - Hexadezimal - Oktal [ Bearbeiten ]
Dual in Dezimal
1010
=
1
⋅
2
3
+
0
⋅
2
2
+
1
⋅
2
1
+
0
⋅
2
0
=
1
⋅
2
3
+
1
⋅
2
1
=
8
+
2
=
10
{\displaystyle 1010=1\cdot 2^{3}+0\cdot 2^{2}+1\cdot 2^{1}+0\cdot 2^{0}=1\cdot 2^{3}+1\cdot 2^{1}=8+2=10}
Dezimal in Dual
Beispiel mit Dezimalzahl 41
41
:
2
=
20
R
e
s
t
1
20
:
2
=
10
R
e
s
t
0
10
:
2
=
5
R
e
s
t
0
5
:
2
=
2
R
e
s
t
1
2
:
2
=
1
R
e
s
t
0
1
:
2
=
0
R
e
s
t
1
↑
{\displaystyle \left.{\begin{matrix}41&:2&=&20&\mathrm {Rest} \ \ \mathbf {1} \\20&:2&=&10&\mathrm {Rest} \ \ \mathbf {0} \\10&:2&=&5&\mathrm {Rest} \ \ \mathbf {0} \\5&:2&=&2&\mathrm {Rest} \ \ \mathbf {1} \\2&:2&=&1&\mathrm {Rest} \ \ \mathbf {0} \\1&:2&=&0&\mathrm {Rest} \ \ \mathbf {1} \end{matrix}}\ \right\uparrow }
Ergebnis: 101001
Hexadezimal in Dezimal
4
F
E
=
4
⋅
16
2
+
15
⋅
16
1
+
14
⋅
16
0
=
1278
{\displaystyle 4FE=4\cdot 16^{2}+15\cdot 16^{1}+14\cdot 16^{0}=1278}
Dezimal in Hexadezimal
Beispiel mit Dezimalzahl 1278
1278
:
16
=
79
R
e
s
t
14
79
:
16
=
4
R
e
s
t
15
4
:
16
=
0
R
e
s
t
4
↑
{\displaystyle \left.{\begin{matrix}1278&:16&=&79&\mathrm {Rest} \ \ \mathbf {14} \\79&:16&=&4&\mathrm {Rest} \ \ \mathbf {15} \\4&:16&=&0&\mathrm {Rest} \ \ \mathbf {4} \\\end{matrix}}\ \right\uparrow }
Ergebnis: 4FE
Oktal in Dezimal
172
=
1
⋅
8
2
+
7
⋅
8
1
+
2
⋅
8
0
=
122
{\displaystyle 172=1\cdot 8^{2}+7\cdot 8^{1}+2\cdot 8^{0}=122}
Dezimal in Oktal
Beispiel mit Dezimalzahl 122
122
:
8
=
15
R
e
s
t
2
15
:
8
=
1
R
e
s
t
7
1
:
8
=
0
R
e
s
t
1
↑
{\displaystyle \left.{\begin{matrix}122&:8&=&15&\mathrm {Rest} \ \ \mathbf {2} \\15&:8&=&1&\mathrm {Rest} \ \ \mathbf {7} \\1&:8&=&0&\mathrm {Rest} \ \ \mathbf {1} \\\end{matrix}}\ \right\uparrow }
Ergebnis: 172
Y
=
A
∧
B
{\displaystyle Y=A\wedge B}
Y
=
A
⋅
B
{\displaystyle Y=A\cdot B}
Y
=
A
B
{\displaystyle Y=A\,B}
A
B
Y
0
0
0
0
1
0
1
0
0
1
1
1
weitere Bildinformationen über Formelsammlung Elektrotechnik: AND-Glied
Y
=
A
∨
B
{\displaystyle Y=A\vee B}
Y
=
A
+
B
{\displaystyle Y=A+B\,}
A
B
Y
0
0
0
0
1
1
1
0
1
1
1
1
weitere Bildinformationen über Formelsammlung Elektrotechnik: OR-Glied
Y
=
A
∧
B
¯
{\displaystyle Y={\overline {A\wedge B}}}
Y
=
A
∧
¯
B
{\displaystyle Y=A{\overline {\wedge }}B}
Y
=
A
B
¯
{\displaystyle Y={\overline {A\,B}}}
A
B
Y
0
0
1
0
1
1
1
0
1
1
1
0
weitere Bildinformationen über Formelsammlung Elektrotechnik: NAND-Glied
Y
=
A
∨
B
¯
{\displaystyle Y={\overline {A\vee B}}}
Y
=
A
∨
¯
B
{\displaystyle Y=A{\overline {\vee }}B}
Y
=
A
+
B
¯
{\displaystyle Y={\overline {A+B}}}
A
B
Y
0
0
1
0
1
0
1
0
0
1
1
0
weitere Bildinformationen über Formelsammlung Elektrotechnik: NOR-Glied
Y
=
A
∨
_
B
{\displaystyle Y=A\,{\underline {\lor }}\,B}
Y
=
A
⊕
B
{\displaystyle Y=A\oplus B}
A
B
Y
0
0
0
0
1
1
1
0
1
1
1
0
weitere Bildinformationen über Formelsammlung Elektrotechnik: XOR-Glied
Y
=
A
∨
_
B
¯
{\displaystyle Y={\overline {A\,{\underline {\lor }}\,B}}}
Y
=
A
∨
_
¯
B
{\displaystyle Y=A\,{\overline {\underline {\lor }}}\,B}
Y
=
A
⊕
B
¯
{\displaystyle Y={\overline {A\oplus B}}}
A
B
Y
0
0
1
0
1
0
1
0
0
1
1
1
weitere Bildinformationen über Formelsammlung Elektrotechnik: XNOR-Glied
[ Bearbeiten ]
Beispiel an einer UND-Verknüpfung:
Y
=
A
∧
B
∧
C
=
A
∧
C
∧
B
=
B
∧
A
∧
C
=
C
∧
B
∧
A
{\displaystyle Y=A\wedge B\wedge C=A\wedge C\wedge B=B\wedge A\wedge C=C\wedge B\wedge A}
Beispiel an einer ODER-Verknüpfung:
Y
=
A
∨
B
∨
C
=
A
∨
C
∨
B
=
B
∨
A
∨
C
=
C
∨
B
∨
A
{\displaystyle Y=A\vee B\vee C=A\vee C\vee B=B\vee A\vee C=C\vee B\vee A}
Beispiel an einer UND-Verknüpfung:
Y
=
A
∧
B
∧
C
=
(
A
∧
B
)
∧
C
=
(
B
∧
C
)
∧
A
=
(
A
∧
C
)
∧
B
{\displaystyle Y=A\wedge B\wedge C=(A\wedge B)\wedge C=(B\wedge C)\wedge A=(A\wedge C)\wedge B}
Beispiel an einer ODER-Verknüpfung:
Y
=
A
∨
B
∨
C
=
(
A
∨
B
)
∨
C
=
(
B
∨
C
)
∨
A
=
(
A
∨
C
)
∨
B
{\displaystyle Y=A\vee B\vee C=(A\vee B)\vee C=(B\vee C)\vee A=(A\vee C)\vee B}
Beispiel in konjunktiver Form:
Y
=
(
A
∧
B
)
∨
(
A
∧
C
)
=
A
∧
(
B
∨
C
)
{\displaystyle Y=(A\wedge B)\vee (A\wedge C)=A\wedge (B\vee C)}
Beispiel in disjunktiver Form:
Y
=
(
A
∨
B
)
∧
(
A
∨
C
)
=
A
∨
(
B
∧
C
)
{\displaystyle Y=(A\vee B)\wedge (A\vee C)=A\vee (B\wedge C)}
[ Bearbeiten ]
Umwandlung einer NAND-Verknüpfung in eine ODER-Verknüpfung
A
∧
B
¯
=
A
¯
∨
B
¯
{\displaystyle {\overline {A\wedge B}}={\overline {A}}\vee {\overline {B}}}
Umwandlung einer NOR-Verknüpfung in eine UND-Verknüpfung
A
∨
B
¯
=
A
¯
∧
B
¯
{\displaystyle {\overline {A\vee B}}={\overline {A}}\wedge {\overline {B}}}
Bild 1 Bild 2
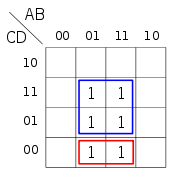
Vereinfachung einer Funktion mit einen KV-Diagramm [ Bearbeiten ] Übetrage aus der Wertetabelle alle Kombinationen mit Hilfe der Disjunktive Normalform (DNF) X = 1 oder der Konjunktive Normalform (KNF) X = 0 in das KV-Diagramm
Fasse die benachbarten Felder zu Blöcken zusammen.
Bild 4
Lese bei X = 1 die UND-Terme, bei X = 0 die ODER-Terme ab.
Beim Beispiel lautet die Vereinfachung bei X = 1
Y
=
(
C
∧
D
)
∨
(
C
∧
D
¯
)
{\displaystyle Y=(C\wedge D)\vee (C\wedge {\overline {D}})}