Formelsammlung Mathematik: Logik

↑ Formelsammlung Mathematik

Aussagenlogik

Boolesche Algebra

UND	ODER
$A\land B\Leftrightarrow B\land A$	$A\lor B\Leftrightarrow B\lor A$	Kommutativgesetze
$A\land (B\land C)\Leftrightarrow (A\land B)\land C$	$A\lor (B\lor C)\Leftrightarrow (A\lor B)\lor C$	Assoziativgesetze
$A\land A\Leftrightarrow A$	$A\lor A\Leftrightarrow A$	Idempotenzgesetze
$A\land 1\Leftrightarrow A$	$A\lor 0\Leftrightarrow A$	Neutralitätsgesetze
$A\land 0\Leftrightarrow 0$	$A\lor 1\Leftrightarrow 1$	Extremalgesetze
$A\land {\overline {A}}\Leftrightarrow 0$	$A\lor {\overline {A}}\Leftrightarrow 1$	Komplementärgesetze
${\overline {A\land B}}\Leftrightarrow {\overline {A}}\lor {\overline {B}}$	${\overline {A\lor B}}\Leftrightarrow {\overline {A}}\land {\overline {B}}$	De Morgansche Gesetze
$A\land (A\lor B)\Leftrightarrow A$	$A\lor (A\land B)\Leftrightarrow A$	Absorptionsgesetze

Distributivgesetze:

1. $A\land (B\lor C)\Leftrightarrow (A\land B)\lor (A\land C)$
2. $A\lor (B\land C)\Leftrightarrow (A\lor B)\land (A\lor C)$

Involution:

${\overline {\overline {A}}}\Leftrightarrow A$

Zweistellige Funktionen

A	B	Wert
0	0	a
0	1	b
1	0	c
1	1	d

Nr.	dcba	Fkt.	Name
0	0000	$0$	Kontradiktion
1	0001	${\overline {A\lor B}}$
2	0010	${\overline {B\Rightarrow A}}$
3	0011	${\overline {A}}$
4	0100	${\overline {A\Rightarrow B}}$
5	0101	${\overline {B}}$
6	0110	$A\oplus B$	Kontravalenz
7	0111	${\overline {A\land B}}$
8	1000	$A\land B$	Konjunktion
9	1001	$A\Leftrightarrow B$	Äquivalenz
10	1010	$B$
11	1011	$A\Rightarrow B$	Implikation
12	1100	$A$
13	1101	$B\Rightarrow A$
14	1110	$A\lor B$	Disjunktion
15	1111	$1$	Tautologie

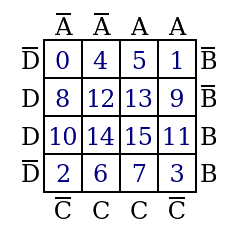
Darstellung mit Negation, Konjunktion und Disjunktion

1. $A\Rightarrow B\iff {\overline {A}}\lor B$
2. $(A\Leftrightarrow B)\iff ({\overline {A}}\land {\overline {B}})\lor (A\land B)$
3. $A\oplus B\iff ({\overline {A}}\land B)\lor (A\land {\overline {B}})$

Vorlagen für KV-Diagramme

Tautologien

Modus ponens:

$(A\Rightarrow B)\land A\implies B$

Modus tollens:

$(A\Rightarrow B)\land {\overline {B}}\implies {\overline {A}}$

Modus tollendo ponens:

$(A\lor B)\land {\overline {A}}\implies B$

Modus ponendo tollens:

${\overline {A\land B}}\land A\implies {\overline {B}}$

Kontraposition:

$A\Rightarrow B\iff {\overline {B}}\Rightarrow {\overline {A}}$

Beweis durch Widerspruch:

$({\overline {A}}\Rightarrow B\land {\overline {B}})\implies A$

Zerlegung einer Äquivalenz:

$(A\Leftrightarrow B)\iff (A\Rightarrow B)\land (B\Rightarrow A)$

Kettenschluss:

$(A\Rightarrow B)\land (B\Rightarrow C)\implies (A\Rightarrow C)$

Ringschluss:

$(A\Rightarrow B)\land (B\Rightarrow C)\land (C\Rightarrow A)$

$\implies (A\Leftrightarrow B)\land (A\Leftrightarrow C)\land (B\Leftrightarrow C)$

Ringschluss, allgemein:

$(A_{1}\Rightarrow A_{2})\land \ldots \land (A_{n-1}\Rightarrow A_{n})\land (A_{n}\Rightarrow A_{1})$

$\implies \forall i,j\,[A_{i}\Leftrightarrow A_{j}]$

Regeln zum Tableaukalkül

φ∧ψ φ ψ

¬(φ∧ψ) ¬φ ¬ψ

φ∨ψ φ ψ

¬(φ∨ψ) ¬φ ¬ψ

φ→ψ ¬φ ψ

¬(φ→ψ) φ ¬ψ

φ↔ψ φ ψ ¬φ ¬ψ

¬(φ↔ψ) φ ¬ψ ψ ¬φ

Schlussregeln

Modus ponens:

$\{\varphi ,\varphi \rightarrow \psi \}\vdash \psi$

Metatheoreme

Sei $M=\{\varphi _{1},\ldots ,\varphi _{n}\}$ eine endliche Menge von Formeln.

Korrektheit der Aussagenlogik.

Es gilt:

$(M\vdash \psi )\implies (M\models \psi ).$

Vollständigkeit der Aussagenlogik.

Es gilt:

$(M\models \psi )\implies (M\vdash \psi ).$

Deduktionstheorem (syntaktisch).

Es gilt:

$(M\cup \{\varphi \}\vdash \psi )\iff (M\vdash \varphi \rightarrow \psi ).$

Infolge gilt auch:

$(\{\varphi _{1},\ldots ,\varphi _{n}\}\vdash \psi )\iff (\vdash \varphi _{1}\land \ldots \land \varphi _{n}\rightarrow \psi ).$

Deduktionstheorem (semantisch).

Es gilt:

$(M\cup \{\varphi \}\models \psi )\iff (M\models \varphi \rightarrow \psi ).$

Infolge gilt auch:

$(\{\varphi _{1},\ldots ,\varphi _{n}\}\models \psi )\iff (\models \varphi _{1}\land \ldots \land \varphi _{n}\rightarrow \psi ).$

Einsetzungsregel.

Sei v eine logische Variable. Ist φ eine tautologische Formel, dann ergibt sich wieder eine tautologische Formel, wenn man jedes Vorkommen von v in φ durch eine Formel ψ ersetzt. Formal:

$(\models \varphi )\implies (\models \varphi [v:=\psi ]).$

Das gilt auch für die simultane Substitution:

$(\models \varphi )\implies (\models \varphi [v_{1}:=\psi _{1},\ldots ,v_{n}:=\psi _{n}]).$

Beispiel. Man überzeugt sich z. B. mittels einer Wahrheitstabelle von

$\models A\land (A\rightarrow B)\rightarrow B.$

Unter Anwendung der Einsetzungsregel lassen sich die zwei Variablen simultan gegen Formeln austauschen:

$\models \varphi \land (\varphi \rightarrow \psi )\rightarrow \psi .$

Zieht man nun die Vollständigkeit und das Deduktionstheorem heran, ergibt sich der Modus ponens:

$\{\varphi ,\varphi \rightarrow \psi \}\vdash \psi .$

Syntax der Aussagenlogik

Definition. Formale Sprache der Aussagenlogik.

Sei $V=\{A_{1},A_{2},A_{3},\ldots \}$ die Menge der logischen Variablen.

Die Menge der wohlgeformten Formeln ist durch die folgende formale Grammatik definiert:

1. Bei 0 und 1 handelt es sich um Formeln.
2. Jede Variable aus V ist eine Formel.
3. Sind φ und ψ Formeln, dann sind es auch $(\neg \varphi ),(\varphi \land \psi ),(\varphi \lor \psi ),(\varphi \rightarrow \psi ),(\varphi \leftrightarrow \psi )$.

Die Menge der wohlgeformten Formeln ist die formale Sprache der Aussagenlogik.

Bemerkung:

1. Für die Praxis wird $V=\{A,B,C,\ldots \}$ definiert.
2. Außerdem können Klammernpaare wie bei Punktrechnung-vor-Strichrechnung weggelassen werden, wobei die Bindungsstärke in absteigender Reihenfolge $\neg ,\land ,\lor ,\rightarrow ,\leftrightarrow$ ist.
3. Anstelle von $\neg \varphi$ wird auch ${\overline {\varphi }}$ geschrieben.

Formales System der Aussagenlogik

Definition. Formales System der Aussagenlogik.

Einzige Schlussregel. Modus ponens:

(MP) $\{\varphi ,\varphi \rightarrow \psi \}\vdash \psi .$

Axiome.

(A1) $\varphi \rightarrow (\psi \rightarrow \varphi )$,

(A2) $(\varphi \rightarrow (\psi \rightarrow \chi ))\rightarrow ((\varphi \rightarrow \psi )\rightarrow (\varphi \rightarrow \chi ))$,

(A3) $(\neg \varphi \rightarrow \neg \chi )\rightarrow (\chi \rightarrow \varphi )$.

Hierbei ist:

• $\varphi \lor \psi$ definiert als $\neg \varphi \rightarrow \psi$,
• $\varphi \land \psi$ definiert als $\neg (\varphi \rightarrow \neg \psi )$,
• $\varphi \leftrightarrow \psi$ definiert als $(\varphi \rightarrow \psi )\land (\psi \rightarrow \varphi )$.

Es folgen historische Axiomatisierungen.

Axiome (Rosser, 1953).

(R1) $\varphi \rightarrow \varphi \land \varphi$,

(R2) $\varphi \land \psi \rightarrow \varphi$,

(R3) $(\varphi \rightarrow \psi )\rightarrow (\neg (\psi \land \chi )\rightarrow \neg (\chi \land \psi ))$.

Axiome (Principia Mathematica, 1910).

(P1) $\varphi \lor \varphi \rightarrow \varphi$,

(P2) $\psi \rightarrow \varphi \lor \psi$,

(P3) $\varphi \lor \psi \rightarrow \psi \lor \varphi$,

(P4) $\varphi \lor (\psi \lor \chi )\rightarrow \psi \lor (\varphi \lor \chi )$,

(P5) $(\psi \rightarrow \chi )\rightarrow (\varphi \lor \psi \rightarrow \varphi \lor \chi )$.

Das Axiom (P4) ist redundant.

Semantik der Aussagenlogik

Definition. Interpretation.

Eine Interpretation $I\colon V\to \{0,1\}$ ist eine Abbildung, die jeder logischen Variablen einen Wahrheitswert zuordnet.

Der Definitionsbereich der Interpretation wird wie folgt auf die Menge der Formeln erweitert:

$I(0)=0$,

$I(1)=1$,

$I(\neg \varphi )=(\neg I(\varphi ))$,

$I(\varphi \land \psi )=(I(\varphi )\land I(\psi ))$,

$I(\varphi \lor \psi )=(I(\varphi )\lor I(\psi ))$,

$I(\varphi \rightarrow \psi )=(I(\varphi )\rightarrow I(\psi ))$,

$I(\varphi \leftrightarrow \psi )=(I(\varphi )\leftrightarrow I(\psi ))$.

Die rechte Seite der Zeile wird hierbei jeweils nach ihrer Wahrheitstabelle ausgewertet.

Definition. Modell.

Eine Interpretation $I$ heißt Modell von $\varphi$, wenn $I(\varphi )=1$ gilt. Kurz:

$(I\models \varphi )\;:\Longleftrightarrow \;I(\varphi )=1.$

Sei $M=\{\varphi _{1},\ldots ,\varphi _{n}\}$ eine Menge von Formeln. Eine Interpretation $I$ heißt Modell von M, wenn $I$ ein Modell jeder Formel aus M ist. Kurz:

$(I\models M)\;:\Longleftrightarrow \;\forall \varphi {\in }M\;(I(\varphi )=1).$

Definition. Modellrelation.

Eine Formelmenge M modelliert eine Formel ψ, wenn jedes Modell von M auch ein Modell von ψ ist. Kurz:

$(M\models \psi )\;:\Longleftrightarrow \;\forall I[(I\models M)\implies (I\models \psi )].$

Definition. Tautologie.

Eine Formel wird tautologisch (allgemeingültig) genannt, wenn jede Interpretation für sie auch ein Modell ist. Kurz:

$(\models \varphi )\;:\Longleftrightarrow \;\forall I(I(\varphi )=1).$

Eine Formel ist genau dann tautologisch, wenn sie durch die leere Menge modelliert wird:

$(\models \varphi )\iff (\{\}\models \varphi ).$

Definition. Erfüllbare Formel.

Eine Formel wird erfüllbar genannt, wenn sie ein Modell besitzt. Kurz:

$\operatorname {erf} [\varphi ]\;:\Longleftrightarrow \;\exists I(I(\varphi )=1).$

Definition. Unerfüllbare Formel.

Eine Formel wird unerfüllbar genannt, wenn sie kein Modell besitzt. Kurz:

$\neg \operatorname {erf} [\varphi ]\iff \forall I(I(\varphi )=0).$

Definition. Erfüllbarkeitsäquivalenz.

Zwei Formeln φ und ψ heißen erfüllbarkeitsäquivalent, wenn gilt:

$\operatorname {erf} [\varphi ]\iff \operatorname {erf} [\psi ].$

Das Modell der ersten Formel braucht dabei nicht mit dem Modell der zweiten Formel übereinzustimmen.

Prädikatenlogik

Rechenregeln

Verneinung (De Morgansche Gesetze):

1. $\neg \forall x[P(x)]\iff \exists x[\neg P(x)]$
2. $\neg \exists x[P(x)]\iff \forall x[\neg P(x)]$

Verallgemeinerte Distributivgesetze:

1. $P\land \exists x[Q(x)]\iff \exists x[P\land Q(x)]$
2. $P\lor \forall x[Q(x)]\iff \forall x[P\lor Q(x)]$

Verallgemeinerte Idempotenzgesetze:

1. $\exists x{\in }M\,[P]\iff (M\neq \{\})\land P\iff {\begin{cases}P&{\text{wenn}}\;M\neq \{\}\\0&{\text{wenn}}\;M=\{\}\end{cases}}$
2. $\forall x{\in }M\,[P]\iff (M=\{\})\lor P\iff {\begin{cases}P&{\text{wenn}}\;M\neq \{\}\\1&{\text{wenn}}\;M=\{\}\end{cases}}$

Äquivalenzen:

1. $\forall x\forall y[P(x,y)]\iff \forall y\forall x[P(x,y)]$
2. $\exists x\exists y[P(x,y)]\iff \exists y\exists x[P(x,y)]$
3. $\forall x[P(x)\land Q(x)]\iff \forall x[P(x)]\land \forall x[Q(x)]$
4. $\exists x[P(x)\lor Q(x)]\iff \exists x[P(x)]\lor \exists x[Q(x)]$
5. $\forall x[P(x)\Rightarrow Q]\iff \exists x[P(x)]\Rightarrow Q$
6. $\forall x[P\Rightarrow Q(x)]\iff P\Rightarrow \forall x[Q(x)]$
7. $\exists x[P(x)\Rightarrow Q(x)]\iff \forall x[P(x)]\Rightarrow \exists x[Q(x)]$

Implikationen:

1. $\exists x\forall y[P(x,y)]\implies \forall y\exists x[P(x,y)]$
2. $\forall x[P(x)]\lor \forall x[Q(x)]\implies \forall x[P(x)\lor Q(x)]$
3. $\exists x[P(x)\land Q(x)]\implies \exists x[P(x)]\land \exists x[Q(x)]$
4. $\forall x[P(x)\Rightarrow Q(x)]\implies (\forall x[P(x)]\Rightarrow \forall x[Q(x)])$
5. $\forall x[P(x)\Leftrightarrow Q(x)]\implies (\forall x[P(x)]\Leftrightarrow \forall x[Q(x)])$

Endliche Mengen

Sei $M=\{x_{1},\ldots ,x_{n}\}$.

1. $\forall x{\in }M\,[P(x)]\iff P(x_{1})\land \ldots \land P(x_{n})$
2. $\exists x{\in }M\,[P(x)]\iff P(x_{1})\lor \ldots \lor P(x_{n})$

Beschränkte Quantifizierung

1. $\forall x{\in }M\,[P(x)]\,:\Longleftrightarrow \,\forall x[x\notin M\vee P(x)]\iff \forall x[x\in M\Rightarrow P(x)]$
2. $\exists x{\in }M\,[P(x)]\,:\Longleftrightarrow \,\exists x[x\in M\wedge P(x)]$
3. $\forall x{\in }M{\setminus }N\,[P(x)]\iff \forall x{\in }M\,[x\notin N\Rightarrow P(x)]$

Quantifizierung über Produktmengen

1. $\exists (x,y)\,[P(x,y)]\iff \exists x\exists y\,[P(x,y)]$
2. $\forall (x,y)\,[P(x,y)]\iff \forall x\forall y\,[P(x,y)]$

Analog gilt

1. $\exists (x,y,z)[P(x,y,z)]\iff \exists x\exists y\exists z\,[P(x,y,z)]$
2. $\forall (x,y,z)[P(x,y,z)]\iff \forall x\forall y\forall z\,[P(x,y,z)]$

usw.

Alternative Darstellung

Sei $P\colon G\to \{0,1\}$ und $M\subseteq G$. Mit $P(M)$ ist die Bildmenge von $P$ bezüglich $M$ gemeint.

1. $\forall x{\in }M\,[P(x)]\iff P(M)=\{1\}\iff M\subseteq \{x{\in }G\mid P(x)\}$
2. $\exists x{\in }M\,[P(x)]\iff \{1\}\subseteq P(M)\iff M\cap \{x{\in }G\mid P(x)\}\neq \{\}$

Substitution

Sei $g\colon M\to N$ eine Injektion. Es gilt:

1. $\forall x{\in }M\,[P(x)]\iff \forall y\in g(M)\,[P(g^{-1}(y))]$
2. $\exists x{\in }M\,[P(x)]\iff \exists y\in g(M)\,[P(g^{-1}(y))]$

Ist $g$ eine bijektive Selbstabbildung auf $M$, so gilt speziell:

1. $\forall x{\in }M\,[P(x)]\iff \forall x{\in }M\,[P(g^{-1}(x))]$
2. $\exists x{\in }M\,[P(x)]\iff \exists x{\in }M\,[P(g^{-1}(x))]$

Eindeutigkeit

Quantor für eindeutige Existenz:

$\exists !x\,[P(x)]$

$:\Longleftrightarrow \;\exists x\,[P(x)\land \forall y\,[P(y)\Rightarrow x=y]]$

$\iff \exists x\,[P(x)]\land \forall x\forall y[P(x)\land P(y)\Rightarrow x=y]$