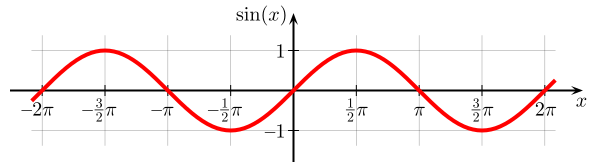
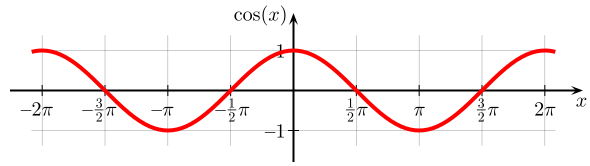

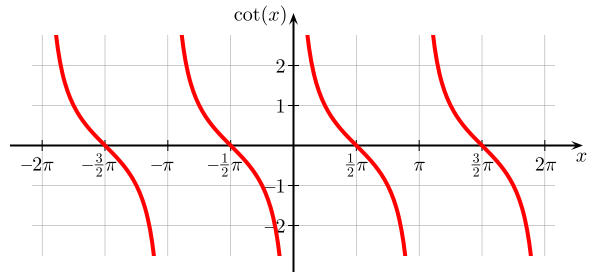


| Punktsymmetrie
|
Achsensymmetrie
|
|

|

|
Definition der Winkel- und Hyperbelfunktionen durch die e-Funktion
[Bearbeiten]

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Gegenseitige Darstellbarkeit von Winkelfunktionen
[Bearbeiten]
|
|
sin
|
cos
|
tan
|
cot
|
sec
|
csc
|
| sin2(x)
|

|

|

|

|

|

|
| cos2(x)
|

|

|

|

|

|

|
| tan2(x)
|

|

|

|

|

|

|
| cot2(x)
|

|

|

|

|

|

|
| sec2(x)
|

|

|

|

|

|

|
| csc2(x)
|

|

|

|

|

|

|
Die Gleichungen gelten für alle  mit Ausnahme der Polstellen. Stetig hebbare Definitionslücken können entsprechend ergänzt werden.
mit Ausnahme der Polstellen. Stetig hebbare Definitionslücken können entsprechend ergänzt werden.
Man beachte, dass die Gleichungen nach dem Wurzelziehen nur betragsmäßig gültig sind, da beim Quadrieren die Vorzeichen verloren gehen.
Winkelfunktionen mit verschobenem Argument
[Bearbeiten]
|
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|











Winkelfunktionen für weitere Vielfache
[Bearbeiten]









Rekursionsformeln mit  :
:

 für
für ![{\displaystyle x\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cedb963595290bb4f2f9e0b1e140ba8432ccd8b)
 für
für ![{\displaystyle x\in [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1d5b7c7f8c8190cb14884785f2aa663f27feff)
 für
für ![{\displaystyle x\in ]-\pi ,\pi [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2dfb61908ceb5f8087682d464288f2f87b5ff5f)
 für
für ![{\displaystyle x\in ]-\pi ,\pi [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2dfb61908ceb5f8087682d464288f2f87b5ff5f)
Aus den Additionstheoremen lassen sich Identitäten ableiten:









![{\displaystyle \sin x\;\sin y\;\sin z={\frac {1}{4}}\left[\sin(x+y-z)+\sin(y+z-x)+\sin(z+x-y)-\sin(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d8ebb9b49c3d0eef86b75f53db923afd399af8)
![{\displaystyle \cos x\;\cos y\;\cos z={\frac {1}{4}}\left[\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)+\cos(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2531ad917e8fd506876febc9afec3be9cfe7e685)
![{\displaystyle \sin x\;\sin y\;\cos z={\frac {1}{4}}\left[-\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)-\cos(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d89dfcd5f8887d058fc58d149fa9a3aca21a32a)
![{\displaystyle \sin x\;\cos y\;\cos z={\frac {1}{4}}\left[\sin(x+y-z)-\sin(y+z-x)+\sin(z+x-y)+\sin(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4742f0e8097b1d543dc9230d0244ab81b5f37888)




























































































































![{\displaystyle x\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cedb963595290bb4f2f9e0b1e140ba8432ccd8b)

![{\displaystyle x\in [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1d5b7c7f8c8190cb14884785f2aa663f27feff)

![{\displaystyle x\in ]-\pi ,\pi [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2dfb61908ceb5f8087682d464288f2f87b5ff5f)










![{\displaystyle \sin x\;\sin y\;\sin z={\frac {1}{4}}\left[\sin(x+y-z)+\sin(y+z-x)+\sin(z+x-y)-\sin(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d8ebb9b49c3d0eef86b75f53db923afd399af8)
![{\displaystyle \cos x\;\cos y\;\cos z={\frac {1}{4}}\left[\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)+\cos(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2531ad917e8fd506876febc9afec3be9cfe7e685)
![{\displaystyle \sin x\;\sin y\;\cos z={\frac {1}{4}}\left[-\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)-\cos(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d89dfcd5f8887d058fc58d149fa9a3aca21a32a)
![{\displaystyle \sin x\;\cos y\;\cos z={\frac {1}{4}}\left[\sin(x+y-z)-\sin(y+z-x)+\sin(z+x-y)+\sin(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4742f0e8097b1d543dc9230d0244ab81b5f37888)



