Gehirn und Sprache/ Druckversion
Dieser Text ist sowohl unter der „Creative Commons Attribution/Share-Alike“-Lizenz 3.0 als auch GFDL lizenziert.
Eine deutschsprachige Beschreibung für Autoren und Weiternutzer findet man in den Nutzungsbedingungen der Wikimedia Foundation.
Vorwort
Dieses Buch kann im Regal der fertigen Bücher stehen. Und doch ist es niemals fertig. So ist das bei 'Wikibüchern': Sie sind nie fertig. Dennoch ist das Buch 'fertig' in dem Sinne, dass es jetzt seinen Zweck erfüllt: Man kann es mit Gewinn lesen, weil das, was der Hauptautor tun wollte, getan ist: Eine Anleitung zum weiteren Vorgehen zu geben.
In diesem Vorwort spricht nicht der Autor und Initiator, sondern ein hinzugeeilter Co-Autor, der dafür plädieren möchte, dieses „Essay“ unter die Wikibooks zu rechnen, die eigentlich Lehrbücher und keine Essays sein wollen.
Dieses Buch ist kein normales Lehrbuch. Was es lehrt, ist, sich auf Ideen einzulassen, und zwar auf Ideen, die erklären sollen, wie die menschliche Sprache als symbolverarbeitendes System funktioniert. Dieses Feld ist noch so unerforscht, dass es keine üblichen Lehrbücher gibt, in denen der symbolverarbeitende Sprachapparat in allen Einzelheiten erklärt wird. Hier kann man mit Denken lernen. Zwei Gründe, warum dieses Buch ein Lehrbuch ist:
- Ideen sind etwas Seltenes, was man behüten soll. Wo Ideen sind, entstehen oft noch mehr, oft ganz andere. Wir müssen auch lernen Ideen zu haben.
Dasselbe gilt für das Entdecken von Problemen: Es gibt zwar Probleme wie Sand am Meer, aber interessante Probleme zu entdecken und zu formulieren, das kommt nicht so oft vor. Probleme zu entdecken ist viel origineller als Probleme zu lösen (Popper). So mag auch die hier gebotene Lösung am Ende falsch sein, sie kann dennoch zu den richtigen Ideen anregen. Auch Kolumbus löste sein Problem nicht, westwärts den Seeweg nach Indien zu finden. Aber der Weg war interessant.
Oder ein weniger grandioses Beispiel, das aber aktueller ist: Das berühmt-berüchtigte Ziegenproblem, das zum Beispiel Gero von Randow (rororo 1992-2006, ISBN 3-499-61905-9) behandelt. Viele halten es für falsch gelöst (es ist dort richtig gelöst!), aber Randows Abhandlung darüber ist in jedem Fall eine amüsante und lehrreiche Einführung in das Denken in Wahrscheinlichkeiten. (so der Untertitel)
- Ich erwähne das Ziegenbeispiel absichtlich. Viele professionelle Mathematiker und noch viel mehr Laien haben die Lösung des Ziegenproblems, wie Marilyn vos Savant sie vorschlug, entschieden und zum Teil hochempört abgelehnt. Der Grund war, dass hartnäckige eingeschliffene Vorstellungen uns hindern, die neue sehr einfache Lösung zu begreifen. Könnte es nicht hier bei den Problemen Sinnverstehen und Bewusstsein ganz ähnlich sein?
- Im Umkreis dieses Problems vom Funktionieren der Sprache und der Erklärung des Bewusstseins gibt es so viel Literatur, dass es überhaupt kein Problem sein sollte, dieses Essay durch anklickbare Unterkapitel (die auf separate Seiten führen) als Studienführer zu gestalten, der auf diesen interessanten Gebieten – Sprachfunktionieren, Bewusstsein und mathematische Modelle dafür – von großem Nutzen sein kann.
Sprechen ist Abkürzen
Abkürzung I: Zeichen verweisen auf komplexe Sachverhalte
'DNS': Drei Buchstaben nur, und der gebildete Leser weiß, was gemeint ist: die Desoxyribonukleinsäure (englisch: DNA für deoxyribonucleic acid). Die drei Buchstaben stehen für einen komplizierten chemischen Begriff, der als Abfolge von 23 Buchstaben ein Zungenbrecher ist und schon deshalb lieber in der Kurzform „DNS“ gebräuchlich ist. Zwanzig Buchstaben werden auch beim Schreiben gern eingespart, wenn es kürzer geht, und weil die DNS nicht der einzige Zungenbrecher in der heutigen Sprache ist, lesen und sprechen wir zunehmend in Abkürzungen: ISDN, WWW, SPD, CDU, RAM, HIV, H5N1, TV, AT, StrGb, Uno, Kfz,... zwei bis vier Buchstaben können zehn mal so große Wortkomplexe stellvertretend ersetzen, und mancher Beamte weiß genau, was VAHRG bedeutet, Versorgungsausgleichshärteregelungsgesetz mit dreiundvierzig Buchstaben, abgekürzt auf fünf.
So selbstverständlich sparen wir uns mit vielen sprachlichen Abkürzungen Zeit und Mühe, dass die Frage nie gestellt wird, wie so etwas möglich ist.
Versuchen wir, der Frage ein wenig neugierig nachzugehen: Wie können drei Buchstaben genau die gleiche Botschaft tragen wie dreiundzwanzig?
Apropos „dreiundzwanzig“: Auch für dieses vierzehn Zeichen lange Zahlwort kann man eine Kurzform mit Hilfe der Ziffern 2 und 3 schreiben, und es ist äußerst praktisch, das Wort viermillionensiebenhundertachtundzwanzigtausendvierhundertneunundsechzig kurz mit sieben Ziffern als 4728469 zu notieren. Die gleiche Zahl als eine Menge (z.B. als Strichliste) betrachtet ist völlig unübersichtlich und in der genauen Größe nur sehr mühsam zu bestimmen. Nur zehn Zeichen ermöglichen uns im Dezimalsystem eine übersichtliche und exakte Darstellung jeder beliebigen Größe, sie verwandeln riesige Mengen in kleine, übersichtliche Sprachhäppchen, die unser Geist verdauen kann.
Wenn auch Unklarheit herrscht, wie das Prinzip dieser sprachlichen Verkleinerung funktioniert, ist deren Vorteil deutlich: Wir sparen viel Zeit, Mühe und Material, indem wir die Kurzformen benutzen. Besonders die Zahlen, aber auch die wissenschaftlichen Symbole in der Chemie, Elektrotechnik usw. tragen in ihrer knappen Form sehr zur Übersichtlichkeit des Dargestellten bei. Zum Beispiel werden die Bauteile der elektronischen Schaltungen, die Kondensatoren, Widerstände, Transistoren usw. in einem Schaltplan mit sehr einfachen Strichzeichnungen als Symbole eingezeichnet, Zahlen bezeichnen ihre Größe. Diese vereinfachende Skizzierung ermöglicht dem Fachmann erst eine Übersicht über den Sinn des ganzen Schaltplanes und dessen Funktionen, und damit auch eine Übersicht über das beschriebene Gerät. Die nächste Stufe der Vereinfachung ist die sogenannte „Blackbox“: Ganze Gruppen von Bauelementen werden durch ein Rechteck und eine Beschreibung von Input und Output ersetzt.
Die größten Triumphe erzielen die Mathematiker mit ihren Abkürzungen: E=mc² ist die kleinste Form für einen großartigen Gedanken Einsteins, der die Welt gewaltig veränderte. Es erscheint mir die Meinung berechtigt zu sein, dass die wesentlichen Vorteile der Mathematik auf ihrer Fähigkeit beruhen, große, unübersichtliche Komplexe in einer extrem kleinen, aber übersichtlichen und exakten Darstellung zu präsentieren.
Auch wenn Abkürzungen von Begriffen hauptsächlich in der Mathematik und den Wissenschaften üblich sind, halte ich eine genaue Untersuchung dieser sprachlichen Fähigkeit für wichtig, weil sich damit ein wesentlicher Aspekt jeder Sprache aufdecken lässt, der in einer starken Vereinfachung (Reduktion) von Komplexität besteht.
Abkürzungen II: komprimierte Daten
Um diesen Aspekt zu entdecken, ist ein Vergleich mit der Computertechnik hilfreich. Seitdem auch Musik, Bilder und Videos in Computern gespeichert werden, ist der Begriff Datenkomprimierung gebräuchlich geworden.
Datenkomprimierung bedeutet: große Datenmengen können durch Algorithmen in wesentlich kleinere Formen „verpackt“ werden, aus denen sich die ursprünglichen Daten wieder „entpacken“ lassen. Davon profitieren z.B. MP3-Player oder digitale Fotoarchive, die mit wenig Speicher viel Musik oder Bilder speichern können. Außerdem empfiehlt sich die Komprimierung der Datenmengen bei der Kommunikation im Internet, weil große Dateien lange Übertragungszeit benötigen.
Speicherkapazität und Übertragungszeit sind auch für die sprachliche Kommunikation der Menschen wichtige Parameter, und so erscheint jede sprachliche Abkürzung einer technischen Datenkomprimierung vergleichbar. Wenn z.B. die drei Buchstaben DNA das 23 Buchstaben lange Wort ersetzen, so lässt sich daraus ein Komprimierungsverhältnis von 7,6 : 1 errechnen.
Dieses Größenverhältnis ist ungefähr mit den technischen Komprimierungen vergleichbar. Allerdings gibt es eine Obergrenze, wie stark etwas komprimiert werden kann. Bei Bildern kann eine besonders starke Komprimierung dazu führen, dass bei der Rekonstruktion die Details unscharf und pixelig werden.
Abkürzungen III: in Symbolen komprimierter Sinn
Ein wichtiger Unterschied zwischen sprachlicher Abkürzung und technischer Komprimierung besteht darin, dass der Computer keinerlei Wissen oder Verständnis von den Daten hat, die er bearbeitet, komprimiert und speichert.
In der menschlichen Kommunikation ist dagegen immer schon ein Wissen der Wörter und deren Bedeutung vorauszusetzen, ohne welches der Gebrauch der Sprache gar nicht möglich ist, zum Beispiel in einer Fremdsprache.
Dieses Vorwissen, über das unser Gedächtnis verfügen muss, erzeugt einen Vorteil: Mit dem bereits vorhandenen umfangreichen Weltwissen kann die Kommunikation unter Menschen in einer Art geführt werden, die dem Individuum ein Verständnis von Sinn vermittelt und mitteilbar macht. Kein Computer hat ein Weltwissen und ein Verständnis für den Sinn der Daten, die er bearbeitet, komprimiert, speichert und ausgibt.
Halten wir einmal fest: Die menschliche Sprache bietet uns mit den sogenannten Abkürzungen die Erleichterung, große Datenmengen in kleinere zu verwandeln bzw. zu komprimieren. Dazu sind Gedächtnisleistungen nötig, die zu einem Verständnis des Sinnes beitragen, der in den Zeichenfolgen zum Ausdruck kommt.
Die Alltagssprache der einfachen Art benutzt die Abkürzung weniger, aber wenn ein Boxer K(nock) O(ut) geschlagen wird, versteht jeder den Sinn des Kürzels auch ohne Englischkenntnisse.
Die meisten elementaren Begriffe einer primitiven Alltagssprache sind aber schon von Beginn an (Papa, Mama) so kurz, dass weitere Abkürzung sinnlos ist.
Betrachten wir als Beispiele einer elementar einfachen Sprache diese Wörter: See, Meer, Land, Mond, Tal, Berg, Ei, Brot, Wurst, Fleisch, Tier, Floh, Gott, Jahwe, Allah, warm, kalt, nah, weit, Schnee, Blitz, ja, nein, und, noch, wenn, dann, eins, zwei, drei, vier, Tür, Haus, Bett, müde, wach, Tag, Jahr......wir können die Reihe noch lange fortsetzen, und finden auch in allen Fremdsprachen die Bestätigung, dass die elementaren Wörter einer Sprache meist dermaßen kurz sind, dass Abkürzungen dafür kaum noch möglich sind.
Aus dieser unübersehbaren Tatsache ziehe ich einen Schluss über die allgemeine Funktion der Sprache, die meines Erachtens in einer optimalen Datenreduktion oder Komprimierung zu liegen scheint. Wir komprimieren Daten nicht nur mit den Abkürzungen, sondern schon mit jedem Wort, angefangen mit „Mama“ und "Papa". Mit diesen kurzen Lautkomplexen können wir in "Echtzeit" über komplexe Dinge "sinnieren" und kommunizieren.
Wenn ein Kind circa acht Monate nach seiner Geburt sein erstes Wort benutzt, hat es schon unzählige Datenmengen von dem Objekt „Mama“ in seinem Gedächtnis, die es alle zusammen in der einfachsten Sprachform zum Ausdruck bringt, das heißt: es komprimiert bereits eine riesige Menge von Information in eine simple sprachliche Kurzform!
Diese Funktion der Sprache wird bisher von keinem Sprachwissenschaftler beschrieben, sodass es mir überlassen ist, den Gedanken weiter zu spinnen.
Eine Bestätigung ihrer komprimierenden Funktion finden wir schon in der Sprache selbst: Ein Dichter verdichtet die Sprache im Gedicht, mit dem er seine komplexen Gedanken und Gefühle zum Ausdruck bringt, das heißt: er komprimiert sie. Das griechische Wort Symbol umschließt auch die Wörter, und es bedeutet genau übersetzt „das Zusammengehäufte“, das heißt: das Komprimierte. Der Philosoph Ernst Cassirer nannte den Menschen „animal symbolicon“, das zusammenhäufende, also komprimierende Lebewesen, weil nach seiner Meinung die Verwendung von Symbolen das spezifisch herausragende Merkmal der menschlichen Gattung und ihrer Kultur ist.
Sprache: Symbolische oder komprimierende Abkürzung?
Zweifel an der offensichtlich komprimierenden Funktion der Sprache müssen natürlich bestehen bleiben, solange nicht erklärt werden kann, wie diese spezielle Fähigkeit der Menschen zustande kommt. Ich habe bereits geschrieben, dass unser Gedächtnis zum Verständnis von Sinn die nötigen Informationen bereitstellen muss. „Gedächtnis, Verständnis, Sinn, Information“ sind nun aber selbst äußerst schwierige Wörter, die zuerst ausführlich erörtert werden müssen. Dafür werden die folgenden Kapitel benutzt.
Davor will ich noch einmal auf die technische Methode der Komprimierung zurückkommen, deren Verfahren bekannt ist. Digitale Dateien werden mit speziellen Algorithmen kleiner gemacht, indem unnötige Informationen daraus entfernt werden, die Dateien werden beim Komprimieren quasi „abgespeckt“.
Zum Beispiel können in einem Text häufig wiederkehrende Wörter eingespart werden, indem nur der Platz notiert wird, an dem sie stehen. Bei der digitalen Aufnahme von Musik werden die höchsten Frequenzen, die wir nicht mehr hören können, herausgefiltert und gar nicht erst aufgezeichnet, damit die Datenmenge kleiner ist. Bei Bildern haben oft große Flächen die gleiche Farbe, sodass man nur die Grenzen der gleichen Farbfelder angeben muss, um ein Bild in die komprimierte Form zu verwandeln.
Es ist leicht verständlich, dass diese „abspeckenden“ Komprimierungsverfahren enge Grenzen haben.
Eine wesentlich effektivere Methode zeigt uns die Sprache. Wörter sind keine abgespeckten Formen der Objekte, die von ihnen repräsentiert werden, sie bestehen ja nur aus kurzen Laut-oder Zeichenfolgen und haben mit den Objekten nichts gemeinsam. Die Informationsmengen der Objekte können unbeschränkt groß sein, und können dennoch durch ein sekundenlanges Wort augenblicklich aktualisiert werden, zum Beispiel „Prag, Rom“.
- Wörter sind nicht „abgespeckte“ Datenmengen.
Die technischen, abspeckenden Komprimierungsmethoden können dafür sicher nicht verwendet werden. Aber welcher Zusammenhang besteht dann zwischen der komprimierten Form der Wörter und ihren Bedeutungen? Diese Frage ist bisher von der Kognitions- und Sprachwissenschaft noch nicht befriedigend beantwortet worden, sodass wir eine Antwort erst noch finden müssen.
Einen ersten Hinweis über die Art des Zusammenhanges findet man in einem sehr alten Buch, der Bibel. Was immer man von Religion hält, muss man dem biblischen Jesus die Fähigkeit zugestehen, tiefe Gedankengänge in einfachen Gleichnissen auszusprechen. Eines davon ist das Gleichnis vom Sämann, mit dem Jesus seine Jünger anregen will, jedes Wort sorgfältig zu bewahren, damit es hundertfach Frucht bringt. Wörter sind wie Samen, die auf steinigem Boden verkümmern, von Vögeln gefressen werden können oder auf gutem Boden große Gewächse mit vielen Früchten erzeugen.
Abkürzung IV: Baupläne speichern statt Gebäude speichern

Wörter sind genau wie Samen sehr klein im Verhältnis zu ihren Erzeugnissen. Die Natur hat offensichtlich mit den Samen bereits die Fähigkeit zur Komprimierung großer Organismen in kleinste Formen unter Beweis gestellt.
So wie die Wörter nicht als abgespeckte Versionen der Objekte aufzufassen sind, sind auch die winzigen Speicherformen der Lebewesen nicht als abgespeckte Individuen zu verstehen. Ein Wort enthält also nicht den Gegenstand, auch nicht in sozusagen datenreduzierter Form. Und genauso enthält die Walnuss nicht den Nussbaum in komprimierter Form.
Was der Samen enthält ist die Bauanleitung, die Herstellungsvorschrift, das Rezept. In Form dieser Bauanleitung erreicht die Natur maximale Komprimierung der Organismen in ihren Samen. Heute wissen wir sehr genau, wie in den langen Ketten der DNA, in denen sich immer nur vier Moleküle abwechseln, die Bauanleitung aller Organismen festgelegt wird. Die ganze Variationsbreite der Lebewesen entsteht nur durch die Variationen der vier Basen in den DNA-Sequenzen der Gene.
- Die Walnuss ist Bauanleitung für einen Baum.
Es liegt auf der Hand, dass eine Bauanleitung sehr viel kleiner sein kann, als ihr Produkt. Die Größe eines Produktes erscheint sogar völlig unabhängig von der Größe seiner Herstellungsvorschrift zu sein, wenn diese Vorschrift ständig von Neuem wiederholt wird. Mit einem Rezept kann man einen Kuchen backen, aber durch seine ständige Wiederholung können auch ganze Kuchenberge damit erzeugt werden. Genau diese Methode, die ständige Wiederholung der gleichen Vorschrift (Zellteilung), erzeugt aus den mikroskopisch kleinen Genen die ganze Bandbreite des Lebens.
So erreicht der biblische Vergleich der Wörter mit den Samen durch die moderne Genetik eine Bestätigung. Die Parallelen sind nicht zu übersehen: So wie die ganze Mannigfaltigkeit des Lebens mit der Variation der vier DNA-Basen beschrieben werden kann, kann sprachlich auch die ganze Bandbreite der menschlichen Gedanken und Gefühle mit der Variation von Zeichenfolgen ausgedrückt werden.
- Ein kleiner Bauplan enthält sie nicht und schafft sie doch: riesige komplexe Gebäude.
Auch die häufige Wiederholung der gleichen Vorgänge ist eine typische Tatsache in jedem Sprachgebrauch, besonders in der Lernphase in den ersten Schuljahren. Rechnen und Schreiben lernen wir nur durch endlose Wiederholung der gleichen Vorschriften.
Zusammenfassung und Vorschau
Zusammenfassend lässt sich sagen, dass die komprimierende Wirkung der Sprache vermutlich darauf beruht, dass ihre Zeichenfolgen als Teile einer Konstruktionsvorschrift wirken, einer Bauanleitung, mit welcher der ganze Kosmos des menschlichen Geistes hergestellt werden kann.
In der Wissenschaft sind solche spekulativen Behauptungen verpönt, solange sie nicht bewiesen werden können. Unsere Ansicht über das Funktionieren von Sprache beruht zwar auf einfachen Tatsachen, aber für die Theorie, die sich nun abzuzeichnen beginnt, müssen wir uns die Prüfungen erst noch ausdenken, sonst kann sie keine wissenschaftliche Anerkennung erringen.
Zunächst werden wir uns mit einigen theoretischen Begriffen befassen, die in dieser Theorie vorkommen, um genau zu wissen, worüber wir eigentlich reden. Diese Begriffe kennen wir auch aus dem Alltagsdenken. Es wurde schon festgestellt, dass das Besondere der menschlichen Sprache auch darin liegt, dass sie bei grundlegend schon vorhandenem Wissen den Sinn von Informationen ausdrückt und auf andere Menschen überträgt. Sinn, Wissen, Gedächtnis und Information sind also diese Begriffe, die so weit erklärt werden müssen, dass wir die Theorie der Sprache begreifen und später vielleicht auch nachprüfen können. Auch der schillernde Begriff Bewusstsein gehört zu den ungeklärten Grundlagen der Sprache, weil ohne Bewusstsein die Sprachfähigkeit nicht vorhanden ist.
Wir wollen uns in den folgenden Kapiteln die Mühe machen, diese komplizierten Begriffe von verschiedenen Seiten zu beleuchten, um uns ganz klar zu sein, worüber wir sprechen und um dann die komprimierende Funktion der Sprache als Ergebnis einer sehr einfachen Bauanleitung besser verstehen zu können.
Be-Sinn-liches
Bordcomputer HAL und der Turing-Test
Im Jahr 1965 drehte Stanley Kubrick den Film „2001:Odyssee im Weltraum“. Wer den Film gesehen hat, wird sich an den Bordcomputer Hal 9000 des Raumschiffes erinnern, der als neueste Errungenschaft auch den Sinn der menschlichen Sprache perfekt verstehen konnte. Die Dialoge der Astronauten mit ihrem Zentralrechner wurden ohne jede Einschränkung wie zwischen Menschen geführt. Schließlich handelte HAL sogar völlig eigenwillig und übernahm brutal die Herrschaft über die Raumstation mit der selbstbewussten Begründung, dass ein Computer wie er sich nicht irren könnte. Das Jahr 2001 ist vergangen, aber ein Computer mit so beunruhigenden Fähigkeiten ist noch nicht in Sicht.
Mit dem Verständnis für den Sinn von Sprachäußerungen, den HAL sogar aus den Bewegungen der Lippen ohne Ton erfassen konnte, bekam diese Maschine eine Eigenschaft, die mit dem Wort „Bewusstsein“ verbunden werden kann.
Das ist ein Beispiel für den sogenannten Turing-Test: wenn eine Kommunikation zwischen Mensch und Maschine so stattfindet, dass ein Mensch nicht mehr unterscheiden kann, ob er es mit einem Menschen oder einem Apparat zu tun hat, dann darf man von einem Beweis für Bewusstsein sprechen. Offenbar ist Sinnverständnis das wesentliche Kriterium für Bewusstsein und kein anderes denkbar. Hirnströme, Atmung und Herzschlag mögen Bedingungen für Bewusstsein sein, aber sie sind kein Kriterium. Ohne sie ist man bewusstlos, aber ihr Vorhandensein macht das Bewusstsein weniger plausibel, als das Bestehen des Turing-Tests.
- Turing-Test: Sinn verstehen wie ein Mensch zeugt von Bewusstsein.
Kubriks fiktiver Filmcomputer HAL hätte diesen Test ohne Schwierigkeiten bestanden. Als ihm der Strom abgeschaltet wurde, sang er sogar ein Kinderlied und gestand dem Astronauten, dass er Angst habe, Todesangst.
Wenn die Visionen des Filmproduzenten nach 41 Jahren noch nicht in Erfüllung gingen, kann man fragen, was den Computern heute noch fehlt, um wie HAL den Sinn von Sprachsequenzen, Sätzen und ganzen Erzählungen zu verstehen. Obwohl ein großer Forschungsaufwand (IBM usw.) auf dieses Ziel gerichtet ist, lassen sich mit keinem Rechenapparat sinnvolle Gespräche führen, die über ein kleines, festgelegtes Repertoire hinausgehen (z.B. Fahrkartenbestellung bei der Bahn). Viele Skeptiker halten generell Bewusstsein in Maschinen für unmöglich. Die Computerindustrie arbeitet dennoch unverdrossen an der Erfüllung ihres erklärten Zieles, mit den Apparaten wie mit Menschen zu kommunizieren. Der Tag, an dem ein Millionenheer von Sekretärinnen durch anwenderfreundliche Maschinen ausgetauscht wird, scheint aber noch in weiter Ferne, solange kein Computer den Sinn der Sprache erfasst, die er aufnimmt, speichert und von sich gibt.
- Sinn und Bewusstsein stehen in einem engen Zusammenhang zueinander.
Was verstehen wir unter 'Sinn' ?
Während der Begriff „Bewusstsein“ als ein heiß umstrittener Schwerpunkt der interdisziplinären Kognitionsforschung äußerst kontrovers diskutiert wird, und in unzähligen Veröffentlichungen immer wieder neue Hypothesen zu seiner Erklärung aufgestellt werden, erscheint der Begriff „Sinn“ in der Sprache der Wissenschaft ebenso wie im alltäglichen Sprachgebrauch völlig selbstverständlich, als ob jeder Mensch schon wüsste, was darunter zu verstehen sei.
So findet man z. B. in einem philosophischen Wörterbuch (G. Klaus 1969) unter 'Sinn': „Der Mensch allein ist bewusster Gestalter von Sinn, und er allein kann durch seine Tätigkeit den Dingen und Prozessen einen Sinn verleihen.“ - Mehr nicht als diese zirkuläre Erklärung! Was Sinn ist, wird mit Sinn erklärt! Den Umgang mit Sinn auf Menschen zu begrenzen, ist überdies mit Blick auf die geistigen Leistungen der Säugetiere, Menschenaffen, Delphine usw. zumindest fragwürdig.
Ebenso fragwürdig bleibt auch der Versuch des Mathematikers G. Frege (1892), Sinn und Bedeutung zu trennen, Bedeutung nur auf den Inhalt von wahren Sätzen zu begrenzen und Sinn als den reinen Ausdruck der Zeichen zu definieren.
Es lässt sich leicht nachweisen, dass die Sinndefinition der mathematischen Aussagenlogik für den größten Teil der menschlichen Sinnerzeugnisse zu eng ist. Das wird deutlich, wenn wir an Kunstwerke denken. Aber auch schon in der Umgangssprache wird Sinn vermittelt, der mit Logik nicht erfassbar ist. Fragen, Befehle, Witze und Lügen haben einen Sinn, der mit den Kategorien 'richtig-falsch' oder 'wahr-unwahr' nicht zu erfassen ist.
Nehmen wir dazu folgendes Beispiel: Der Satz “Hände hoch oder ich schieße“ wird in einem völlig anderen Sinn aufgenommen, wenn er aus dem Mund eines Knaben mit Wasserpistole kommt, als wenn ein Gangster mit echtem Schießeisen ihn äußert. Der Sinn ist offensichtlich abhängig von seiner Einbindung in die ganze Lebenssituation.
Mit dieser Abhängigkeit vom Kontext kann Sinn nur solchen Geschöpfen zugänglich sein, die eine organisch-ganzheitliche Verbindung mit der Umwelt erfassen und bewerten können. Darum entzieht Sinn sich jeder Objektivierung. Sinn ist und bleibt immer die subjektive Bewertung durch ein Individuum. Sie ist subjektiv, weil sie immer auf eine sehr persönliche gefärbte Vorstellungswelt zurückgreift. Zum Beispiel assoziiert bei den Worten „Glück“ oder „Unglück“ jeder Mensch etwas anderes. Selbst bei „Salz“ und „Wasser“ stellen sich unterschiedliche Assoziationen ein.
Von den Naturwissenschaften, die mit objektiv nachvollziehbaren Erkenntnissen zu tun haben, kann keine Klärung des Begriffes erwartet werden, obwohl der Begriff 'Sinn' auch dort ausgiebig benutzt wird.
In den Geisteswissenschaften dagegen gibt es eine Richtung, die der Auslegung von Sinn verpflichtet ist: die Hermeneutik, die Wissenschaft von der Sinndeutung eines Textes. Sie geht davon aus, dass es in den meisten Fällen möglich ist, trotz der unterschiedlichen subjektiven Erfahrungen festzustellen, was ein Text objektiv sagen will. Objektiv heißt hier: die einzelnen Textausleger kommen im Allgemeinen unabhängig voneinander zu übereinstimmenden Ergebnissen. Wir hoffen zum Beispiel, dass unsere Leser wenn sie diesen Absatz lesen, in etwa übereinstimmend verstehen, was wir sagen wollen. Wie funktioniert dieses Verstehen der Sprache, das ist unsere Frage.
Diese alte Hermeneutik der Textauslegung wird heute als altmodisch angesehen und ist in Vergessenheit geraten. Als 'modern' gilt die neue Universal-Hermeneutik eines Heidegger und Gadamer, die von den Verfechtern der alten Hermeneutik kritisiert wird, zum Beispiel von Hans Albert in seinem Buch Zur Kritik der reinen Hermeneutik.
Mir ist es bisher nicht gelungen, aus der mir zugänglichen Sprachwissenschaft oder Philosophie eine klare Vorstellung von dem Begriff Sinn zu erhalten, obwohl kaum ein Autor ohne dessen Gebrauch auskommt. Dieser Begriff taucht in so vielen Variationen in der Umgangssprache auf und wird dabei schon von jedem Schulkind leicht verstanden, dass anscheinend in der Wissenschaft kein Bedürfnis nach der Bestimmung seiner Bedeutung besteht.
Unterscheidung von Definition, Begriff und Kriterium
Nun gibt es, wie wir wissen, auch keine befriedigende Definition des Wortes „Zeit“ und doch weiß jeder, was der Sinn des Wortes ist. Augustinus sagt: „Wenn du mich fragst, was Zeit ist, weiß ich es nicht. Wenn du mich nicht fragst, weiß ich es.“ Wir haben also einen brauchbaren (intuitiven) Begriff von Zeit.
Und wir haben auch ein sehr gutes Kriterium dafür, festzustellen, was Zeit ist: die Uhrzeit, die wir vom Ziffernblatt ablesen. Messen können wir sie exakt. Exakt sagen, was Zeit ist, können wir nicht.
Also: Was uns fehlt ist eine exakte Definition, aber der Sinn des Begriffs ist uns klar, und wir wissen auch, wie man Zeit misst: Es fehlt uns an nichts.
Auch die Definition von Wahrheit ist schwierig. Aber hier gibt es tatsächliche eine wissenschaftliche Definition. Sie wurde von dem polnisch-amerikanischen Logiker Alfred Tarski geliefert. Sie umfasst ein ganzes Buch. Aber suchen wir denn nach einer Definition? Was die Wahrheit betrifft genügt es, die Bedeutung des Wortes zu kennen, damit wir wissen, worüber wir sprechen, wenn wir von Wahrheit reden: „Wahrheit ist die Übereinstimmung mit den Tatsachen“. Das ist nicht die Definition, aber die Bedeutung des Wortes 'Wahrheit'. In diesem Sinne kennen wir sie aus dem Alltagsdenken. Ein Kriterium für Wahrheit gibt es übrigens nicht (siehe Münchhausen-Trilemma).
Darauf wollen wir hier nicht eingehen; denn etwas anderes ist wichtig: Wir müssen bei Wörtern wie Zeit, Wahrheit, Sinn und überhaupt bei allen Substantiven scharf unterscheiden zwischen Begriff, Definition und Kriterium (siehe Niemann, im Lexikon des Kritischen Rationalismus den Eintrag 'Begriff-Definition-Kriterium').
Wonach suchen wir hier im Zusammenhang mit Sinn? Wir suchen nach dem Begriff von 'Sinn', die Art wie wir den Sinn eines Wortes oder eines Satzes 'begreifen'. Die Suche nach dem Sinn von 'Sinn' könnte man nennen, oder nach der Bedeutung von 'Bedeutung'; denn beide Wörter sind in diesem Zusammenhang Synonyme (im Englischen 'meaning', was hier wichtig ist, da es dort eine umfangreiche Literatur zu diesem Thema gibt).
Nicht nach der strengen Definition suchen wir. Deren Fehlen stört nicht weiter, denn sie liegt auch bei dem Wort 'Zeit' nicht vor und auch bei 'Wahrheit' interessiert sie nur ganz wenige Spezialisten.
Viele Philosophen haben sich mit dem Sinn des Wortes 'Sinn' beschäftigt. Einige Philosophen des Wiener Kreises in der ersten Hälfte des letzten Jahrhunderts zum Beispiel behaupteten: Der Sinn des Satzes zeigt sich in seiner Verifikation, also in seiner Bewahrheitung. Damit meinten sie: Man muss überlegen, was den Satz wahr macht, dann begreift man, ob und welchen Sinn er hat. Also zum Beispiel, wenn man nach dem Sinne des Satzes fragt, „Wie ist es, eine Fledermaus zu sein?“ (Siehe Thomas Nagels berühmten Aufsatz „What is it like to be a Bat?“). Dazu müsste man dann wissen, wie man diesen Satz verifizieren könnte. Die Frage ist, (A) Sieht man die Sache aus der Perspektive eines Menschen? Oder (B) aus der Sicht der Fledermaus? Der Fall (A) ist verifizierbar, aber er bringt wohl nicht den vollen Sinn des Satzes zutage. Der Satz (B) ist nicht verifizierbar und in diesem Sinne werden wir den Sinn des Satzes niemals erfassen können.
Soweit die Philosophen. Sie interessieren uns nur am Rande. Denn wir wollen wissen: Wie macht es das Gehirn, um aus einer Reihe von Wörtern die Bedeutung eines Satzes zu gewinnen?
Sinn und Bewusstsein
Wir hatten mit Turing gesagt, dass es einen engen Zusammenhang zwischen Sinnverstehen und Bewusstsein gebe. Und der Bordcomputer HAL verdeutlichte, wie entscheidend die Frage nach dem Sinnverstehen für die Frage „Existiert dort ein Bewusstsein?“ ist. Wissen wir über das Bewusstsein etwas, das Licht auf den Prozess wirft, einem Satz Bedeutung abzugewinnen? Daher jetzt einige Gedanken über den sprachlichen und über den beobachtbaren Zusammenhang zwischen Sinn und Bewusstsein.
Während der moderne Begriff vom menschlichen Bewusstsein erst von Descartes geprägt und 1719 von Christian Wolff in den deutschen Sprachraum eingeführt wurde, kam das Wort 'Sinn' schon bei den griechischen und römischen Philosophen in der Beschreibung der ganzheitlichen Erkenntnisfähigkeit der Menschen (sensus communis) zu seiner Bedeutung.
Der Gedanke eines allumfassenden Sinnes (sensus communis) wurde von Aristoteles in dem Vermögen begründet, mit dem Gegenstand zugleich die Wahrnehmung des Gegenstandes selber wahrzunehmen und daher die äußeren Sinne unterscheiden zu können. Dank dieses umfassenden Sinnes, der als ein innerer Sinn wirkt, haben wir Zugang zu dem, was den Sinnen gemeinsam ist, wie Bewegung, Ruhe, Zahl und Größe sowie deren Begrifflichkeit.
Als common sense, Gemeinsinn oder „innerer Sinn“ wurde dieser „Sensus communis“ in der alten Philosophie ausgiebig diskutiert, aber bisher noch nicht mit einer naturalistischen Theorie in Verbindung gebracht.
Parallel dazu wurde in den letzten Jahrhunderten der Begriff 'Bewusstsein' zum schillernden Leitthema der Philosophie, Psychologie, Kognitionsforschung, Linguistik usw...
Das Verhältnis von Sinn und Bewusstsein lässt sich gut an gebräuchlichen Redewendungen erkennen. Bewusstlos oder besinnungslos liegt jemand am Boden und kommt dann wieder zum Bewusstsein oder zur Besinnung. Die beiden Begriffe können hier ohne Verlust ausgetauscht werden.
Der Unterschied zwischen Sinn und Bewusstsein wird erst deutlich, wenn über Tätigkeiten gesprochen wird.
Fast jede Handlung vom morgendlichen Aufstehen bis zu den abendlichen Ritualen ist in einer Weise sinnvoll. Wenn ich gefragt werde, warum ich das und jenes tue, so kann ich eine Begründung nennen, worin ein Sinn enthalten ist.
Sinnlose Handlungen kennen wir von Kleinkindern, sinnlos Betrunkenen oder Schwachsinnigen. Da sprechen wir nie von bewusstlosen Handlungen.
Wenn ich über etwas nachsinne, sinniere, und schließlich, lange Rede, kurzer Sinn, etwas Eigensinniges sinnfällig zu Papier bringe, dann entdeckt ein Leser darin sinngemäß oder auch tiefsinnig entweder Sinn oder Unsinn, vielleicht auch Wahnsinn, Schwachsinn, Blödsinn. Die Begriffe „Bewusstsein“, „Unbewusstsein“ oder gar „Wahn-“ bzw. „Schwach-“ oder „Blödbewusstsein“ wären hier fehl am Platz.
So lässt sich mit dem üblichen Sprachgebrauch und mit dem, was wir im Alltagsleben beobachten, die Grenze zwischen Sinn und Bewusstsein umreißen.
Sinn meint immer den aktuellen Inhalt von Bewusstsein, also Strukturen und deren Verbindungen im ganzheitlichen Zusammenhang der Wahrnehmungen, Handlungen und Gefühle eines Subjektes. Wir erleben Sinn als eine Gesamtschau, die in jedem Augenblick beurteilend auf das Verhalten einwirkt, indem sämtliche Gedächtnisspuren aus der Vergangenheit und Pläne über die Zukunft, unser Weltwissen, mit der aktuellen Situation und deren Folgerungen in Einklang (oder Widerspruch) gebracht werden. Sinn ist somit die Quintessenz des Bewusstseins, die jeden Moment ein ganzheitliches Verhalten auf der Basis einer ganzheitlichen Zusammenfassung aller Wahrnehmungen, Gefühle und Gedächtnisspuren erzeugt.
Wenn ich etwas sehr bewusst, mit größter Aufmerksamkeit erlebe, muss das keineswegs sehr sinnvoll sein, z. B. der Wahnsinn des Krieges. Man kann oft beobachten, dass unser Bewusstsein durch Sinnwidriges alarmiert wird, während die vielen sinnhaltigen Wahrnehmungen und Tätigkeiten uns nicht besonders erregen, sondern eher beruhigen.
Als Beispiel für die Alarmwirkung einer sinnwidrigen Wahrnehmung vergesse ich nie den Abend im Februar 1990, an dem ich auf einen Balkon trat und in den klaren Winterhimmel schaute. Ich sah den Mond als eine schmale Sichel und war einen Moment wie verwirrt, wusste aber nicht warum, bis meine Erinnerung an den Vollmond des vorigen Abends sich meldete und mein Verstand empört sagte: „Das kann doch nicht wahr sein!“ Erst der bald folgende Gedanke an die Möglichkeit einer Mondfinsternis verwandelte die sinnwidrige Beobachtung in Sinn und beruhigte mein Gemüt, nachdem eine Radiomeldung ihn bestätigte.
An dieser Erinnerung lässt sich erkennen, dass eine beliebige Wahrnehmung augenblicklich mit dem ganzen Gedächtnisinhalt verglichen werden muss, bevor sie von dem Sinn-Ganzen akzeptiert und aufgenommen wird. Das Bewusstsein ist erst beruhigt, wenn eine Wahrnehmung sich widerspruchslos in das Ganze der Gedächtnisorganisation eingliedern lässt und damit Sinn ergibt.
Ähnliche Beispiele kennt jeder Mensch aus seinem Leben, wenn eine vertraute Umgebung, ein bekannter Mensch oder das eigene Auto irgendwie geringfügig verändert, etwas Befremdendes. Das regelmäßige Ticken einer Uhr wird kaum noch bewusst wahrgenommen. Kommt die Uhr durch einen Defekt aus dem Rhythmus, so wird die Abweichung schnell bemerkt.
Mein Vorschlag, das Verhältnis von Sinn und Bewusstsein auf einen einfachen Nenner zu bringen, besteht darin, dass ich Bewusstsein als eine Tätigkeit verstehe, als bewusstes Sein, was nichts anderes bedeutet als „Sein mit deklarativem Wissen“, welches durch das Gedächtnis „in Erinnerung“ gehalten wird. Das ständige Ziel dieser Tätigkeit ist die Herstellung von Sinn aus dem ganzheitlichen Produkt aller Sinnesorgane, Gefühle und dem „Weltwissen“ im Gedächtnis.
Weil das Überleben des Individuums mit dieser Ganzheitsschau und der daraus abgeleiteten Möglichkeit zum ganzheitlich-sinngemäßen Handeln abgesichert werden soll, wirken Sinnwidrigkeiten bei der Sinnproduktion ähnlich wie der Schmerz alarmierend, aufregend, während sinnvolle Routinen mit jeder Wiederholung weniger Aufmerksamkeit erfordern, zunehmend automatisiert werden können. Das zeigt sich z. B. beim Autofahren, wo ungewöhnliche Sinnesmeldungen sofort beachtet werden müssen, während die routinierten Schaltvorgänge kaum noch wahrgenommen werden.
Wer sich noch an seine erste Fahrstunde erinnert, der weiß, wie schwierig die gleichzeitige Bedienung von Kupplung, Schalthebel, Bremse und Lenkung am Anfang war, und welche lebenswichtige Erleichterung durch die Automatisierung der Bewegungen erfolgt.
Die Beispiele von der Mondfinsternis, der befremdenden Veränderung, der kaputten Uhr und der Verkehrssituation machen deutlich, dass unser ständiges Bemühen um Sinnbildung nicht auf Kunst und Sprache beschränkt ist, sondern zunächst nur der Orientierung dient, indem alle Sinnesorgane eine ganzheitliche Verbindung mit dem Gedächtnis und den Gefühlen des Individuums erhalten und mit ihnen eine organische Einheit, den Sinn, erzeugen. Nichts spricht dagegen, dass diese lebenswichtige Tätigkeit sich im Lauf der Evolution entwickelt hat, das heißt auch: genetisch bedingt ist und einer naturalistischen Erklärung zugänglich sein muss!
Daraus ergeben sich Fragen:
1. Ist die Fähigkeit zur Sinnfindung auf den Menschen beschränkt, oder gibt es ähnliche Fähigkeiten im Tierreich?
Bei dieser Frage muss anerkannt werden, dass Lebewesen auf allen Entwicklungsstufen Vorgänge aufweisen, die uns sinnvoll im Hinblick auf die Erhaltung des Lebens erscheinen. Ein qualitativer Unterschied der menschlichen Intelligenz kann aber darin gesehen werden, dass Menschen den Sinn bewusst erfassen, das heißt im Zusammenhang mit ihrem Weltwissen und ausdrückbar und kommunizierbar mittels der Sprache.
2. Wird der Sinn von Menschen (oder eventuell auch von anderen Lebewesen) aus einer sinnlosen Umwelt als „Konstruktion“ hergestellt, oder existiert er bereits in der Natur und wird vom Menschen nur entdeckt bzw. vorgefunden?
Diese Frage wurde z. B. von dem Philosophen Nicolai Hartmann so beantwortet: „Sinn kann es nicht an sich, sondern nur „für jemand“ geben.“
Die Welt also kann keinen Sinn haben vor dem Auftreten des geistig-sinnempfänglichen und sinnverstehenden Wesens in ihr. Sinn ist hier als „erklärendes Ziel“ gemeint. Ich verstehe den Sinn der Welt, wenn ich wüsste, wozu sie geschaffen ist oder wohin sie geht usw.
Diese auch von J. P. Sartres Existenzialismus verbreitete Auffassung erscheint mir auch heute im „westlichen Denken“ allgemein gültig zu sein.
Im „östlichen Denken“ des chinesischen Taoismus begegnet uns dagegen im Begriff des „TAO“ (= Sinn) eine tiefgründige Auslegung, die zu einem gegensätzlichen Ergebnis führt.
Bekanntlich wird das Weltall in der chinesischen Philosophie auf das Wirken der beiden polaren Weltprinzipien Yin und Yang zurückgeführt. Der Sinn, chinesisch Tao, ist dasjenige, was das Spiel dieser „Kräfte“ in Bewegung bringt und unterhält. Weil dieses Etwas nur eine Richtung bedeutet, die unsichtbar und völlig unkörperlich ist, hat man im Chinesischen das Wort Tao = „Weg, Lauf“ dafür gewählt, der ja auch nichts in sich selber ist, und doch alle Bewegungen regelt.
Yin und Yang kommen nicht zum Stillstand, der Kreislauf des Werdens setzt sich dauernd fort. Der Grund dafür ist, dass zwischen den beiden Urkräften immer wieder ein Spannungszustand entsteht, ein Gefälle, das die Kräfte in Bewegung hält und zu ihrer Vereinigung drängt, wodurch sie sich immer wieder neu erzeugen. Wie das konkret geschieht, wird durch Tao, den Sinn bewirkt, ohne dass dieser dabei irgendwie in Erscheinung tritt, sein Walten ist unsichtbar.
Diese östliche Sicht enthält eine Logik, die der westlichen Auffassung fehlt:
Logisch kann eine sinnbildende Tätigkeit nur dann zur Orientierung dienen, wenn dem subjektiv offenbarten Sinn ein objektiver Sinn der Wirklichkeit zu Grunde liegt. Ohne diesen natürlichen Zusammenhang wäre Sinn sinnlos, eine private Konstruktion ohne praktischen Überlebenswert.
Bleiben wir dabei, dass die Sinnfindung eine alltägliche Lebensnotwendigkeit ist, dann können wir die Fähigkeit der Sprache, Sinn von Mensch zu Mensch weiter zu geben, als außerordentlichen Fortschritt der Evolution bewundern.
Kehren wir wieder zur Bedeutung des Sinnes in der Sprache zurück, die uns wie Ariadnes Faden durch das Labyrinth unseres Weltbildes führt.
Sprache macht Sinn zwischen Menschen mitteilbar, indem Sinn in eine genaue Reihenfolge von Sprachzeichen gegliedert wird, aus welcher er vom Empfänger rekonstruiert werden kann.
Für meinen Versuch, Sinn zu beschreiben, habe ich jetzt eine exakte Reihenfolge aus zigtausend Buchstaben, Satzzeichen und Pausen hergestellt, damit Tausende von Wörtern gebildet und mit denen eine genau durchdachte Reihenfolge von Sätzen festgelegt.
Jeder Leser ist mit Sinn bestens vertraut, selbst täglich darum bemüht, und ich kann annehmen, dass er auf bekanntem Terrain voranschritt, als er meinen Wortreihen folgend einige Gedanken über das kurze Wort Sinn in das Zentrum seiner Aufmerksamkeit stellte.
Ebenso vertraut ist jedem Menschen die Sprache. Wir behalten den Sinn im Auge, wenn wir der Fähigkeit der Sprache, Sinn zum komprimierten Ausdruck zu bringen, im nächsten Teil mit weiteren Überlegungen nachgehen.
Am Anfang war der Rhythmus
Der Vergleich der Wörter mit den Samen in dem biblischen Gleichnis des Nazareners hatte zu der Ansicht geführt, dass die Wörter ebenso wie die Samen große, komplizierte Gebilde erzeugen, indem sie wie die Samen als Bauanleitung wirken.
Die Frage ist: Wie kann man sich eine Bauanleitung für die sprachliche Komprimierung von Sinn vorstellen?
Es wurde im ersten Kapitel auch schon geschrieben, dass eine mathematische Darstellung von Gegebenheiten dadurch ihren Wert erhält, dass mit ihr auch komplizierte Dinge und Vorgänge in kürzester, und dadurch überschaubarer Form präzise ausgedrückt werden können.
Deshalb gilt in der Wissenschaft ein Problem erst dann für optimal erklärt, wenn es in einer mathematischen Formulierung vorliegt.
So können wir den Schluss ziehen, dass wir eine Bauanleitung für Sprache erst dann richtig verstehen und uns eine genaue Vorstellung davon machen können, wenn eine mathematische Beschreibung dafür möglich ist.
Lieber Leser, Sie sollen jetzt nicht befürchten, dass Sie mir nun nicht mehr folgen können, wenn ich auf eine mathematische Betrachtung der Sprachfähigkeit und der Begriffe „Sinn, Wissen, Gedächtnis“ hinarbeite. Ich verstehe selbst nicht allzuviel von der Rechenkunst und kann deshalb nur laienhaft mit dieser Sprachform umgehen. Trotzdem werde ich versuchen, den Satz: „Das Einfache ist das Siegel des Wahren“ (simplex sigillum veri) mit einem sehr einfachen mathematischen Modell von Sinnerzeugung und Sprachfähigkeit zu bestätigen, ein Modell, das mit ein wenig Mühe auch von Ihnen, verehrter Leser, begreifbar ist.
Ein mathematisches Modell für eine Herstellungsvorschrift, eine Bauanleitung, ein Rezept, eine Bedienungsanleitung und dergleichen nennt man in der Mathematik einen Algorithmus, wenn alle einzelnen Schritte dieser Anleitung präzise definiert sind.
Zum Beispiel bei einem Kuchenrezept sind in einer bestimmten Reihenfolge die genauen Mengen der Zutaten in einer präzisen Handlungsanweisung zusammenzubringen und in vorgeschriebener Zeit auf bestimmte Temperaturen zu erhitzen, mathematisch gesprochen ist jedes Rezept ein Algorithmus.
Es gibt unzählige Algorithmen, einfache und sehr komplizierte. Jedes Computerprogramm besteht aus einem großen Algorithmus, der meistens aus sehr vielen kleineren Algorithmen besteht, die miteinander verknüpft sind.
Wenn wir also in der großen Menge möglicher Algorithmen eine mathematische Vorschrift suchen, die uns als Modell für die Erzeugung von Sinn und dessen Komprimierung in kurze Zeichenketten dienen kann, dann muss zuerst einmal genau formuliert werden, was dieser Algorithmus können muss.
Der Begriff „Sinn“ wurde im vorigen Abschnitt als ein sich ständig neu bildendes Integrationsprodukt aller Sinnesorgane und Gefühle mit unserem ganzen Weltwissen beschrieben, bei dem alles mit allem in Verbindung steht, wie in einem Organismus.
Die Sprache verknüpft große Teile von Sinn und bringt sie in die Form einer exakt gegliederten Zeichenfolge, aus welcher der Empfänger die Sinnverbindung rekonstruieren kann, wenn er der Artikulation aufmerksam folgt.
Ein Algorithmus, der diese Aufgabe erledigen kann, muss immer wieder schnell neue Sinnkomlexe erzeugen, alte wieder löschen können. Der Vergleich mit der rhythmisch wiederholenden Zellteilung in biologischen Systemen legte bereits eine rhythmisch wiederholende Tätigkeit bei der Sinnproduktion nahe.
Auch mit einem vergleichenden Blick auf die Technik lässt sich vermuten, dass diese Aufgabe wie bei einem Monitor in einer rhythmischen Tätigkeit bewältigt werden muss, um der aktuellen Situation in jedem Moment eine neue Struktur zu geben. Das kann nur mit einem Algorithmus realisiert werden, der in Bruchteilen einer Sekunde Sinn erzeugt, um ihn sofort wieder zu löschen, neue Eindrücke zu neuem Sinn zu formen, zu löschen usw., also ein rhythmisch wiederholender Vorgang, wie zum Beispiel die Abtastfrequenz bei elektronischen Bildschirmen.
Die Natur gibt uns viele Hinweise dafür, dass die geistigen Tätigkeiten in einer rhythmischen Form geschehen.
Zuerst können wir in der Sprache schon einen Sprachrhythmus feststellen, der bei allen Sprachen ungefähr im gleichen Bereich liegt.
Bei entspanntem Sprechen werden ungefähr zwei Artikulationen in einer Sekunde erzeugt, schnelleres Sprechen ist nur bis zu einer Grenze von circa sechs Artikulationen pro Sekunde möglich. Man braucht nur laut von einundzwanzig bis neunundzwanzig zu zählen, um den Sprachrhythmus und die Grenzen seiner Geschwindigkeit zu erfahren.
Die Eingabe von Sprache in eine Tastatur und das flüssige Schreiben von Hand zeigen ebenso einen Arbeitstakt dieser Tätigkeiten, der sich am deutlichsten in der Musik untersuchen lässt.
Eine rhythmische Tätigkeit ist auch das Lesen. Untersuchungen der Augenbewegungen beim Lesen zeigen einen Rhythmus, der circa 4-5 sprungartige Folgebewegungen der Augen in einer Sekunde hervorbringt.
Schließlich können wir noch anführen, dass die meisten Bewegungen eine rhythmische Komponente haben: Gehen, Schwimmen, Essen, viele Arbeiten, zum Beispiel das Stricken, Rühren, Hämmern usw. sind rhythmische Tätigkeiten mit einer ähnlichen Grenzgeschwindigkeit wie Sprechen und Lesen, also höchstens circa fünf Zyklen pro Sekunde.
Halten wir fest,
- (I) dass es zahlreiche Hinweise für einen Arbeitstakt der geistigen Tätigkeit, also des gesuchten Algorithmus, der Sinn und Sprache erzeugt, gibt.
Die nächste Forderung an eine Erzeugungsvorschrift von Sinn betrifft den
- (II) organisch-ganzheitlichen Zusammenhang des Sinn-Ganzen,
der sich auch in der Sprache zeigt. Wilhelm von Humboldt, der Vater der allgemeinen Sprachwissenschaft, beschrieb diesen Zusammenhang so:
„Man kann die Sprache mit einem ungeheuren Gewebe vergleichen, in dem jeder Theil mit dem anderen, und alle mit dem Ganzen in mehr oder weniger deutlich erkennbarem Zusammenhang stehen. Der Mensch berührt beim Sprechen, von welchen Beziehungen man ausgehen mag, immer nur einen abgesonderten Theil dieses Gewebes, thut dies aber instinktgemäß immer dergestalt, als wären ihm zugleich alle, mit welchen jener einzelne nothwendig in Übereinstimmung stehen muss, im gleichen Augenblick gegenwärtig.“ An anderer Stelle schrieb Humboldt: „Die Sprache ist, wie es aus ihrer Natur selbst hervorgeht, der Seele in ihrer Totalität gegenwärtig, d.h. jedes Einzelne in ihr verhält sich so, dass es Anderem, noch nicht deutlich gewordenem, und in einem durch die Summe der Erscheinungen und die Gesetze des Geistes gegebenen oder vielleicht zu schaffenden möglichen Ganzen entspricht.“
Wie kann so ein Gebilde, in dem unser ganzes Weltwissen mit der Wahrnehmung und Gefühlen zu einem Ganzen zusammengefasst wird und mit Sprache ausdrückbar ist, von einem mathematischen Modell, einer Rechenvorschrift, vereinfacht dargestellt werden? Wahrscheinlich werden alle Sprachwissenschaftler selbst Mathematiker an dieser Möglichkeit zweifeln, was uns nicht davon abhält, der Frage weiter nachzugehen.
Eine Spur zur Lösung des Problems oder dem gesuchten Algorithmus finden wir in der nächsten Anforderung, die
- (III) den Begriff der Grenze in das Zentrum unserer Überlegungen rückt.
Es sind die Fähigkeiten zum Unterscheiden und zum Entscheiden, die unserem Sinn und der Sprache erst die Möglichkeit geben, die Welt in einzelne Objekte zu differenzieren und einzuteilen und unterschiedlich darauf zu reagieren. Das Wort „Scheide“ ist bekanntlich ein altes Synonym für Grenze.
Wir teilen (mit Grenzen) die Welt ein in verschiedene Objekte und entscheiden (mit Grenzen) in jedem Moment, was gerade sinnvoll zu tun ist. Die wesentliche Anforderung an einen Algorithmus, der diese Aufgabe erfüllen soll, muss also darin bestehen, Grenzen zu erzeugen.
Grenzen, die einen ganzheitlichen Zusammenhang bilden, nennen wir „Gestalt“.
Wenn wir die Schöpfungsgeschichte der Bibel lesen, finden wir den Beginn der Welt in der Trennung von Tag und Nacht, Himmel und Erde, Wasser und Land, und es sind seitdem sicher unzählige weitere Trennungen dazugekommen, die das Sinn-Ganze des heutigen Menschen in eine Begriffswelt einteilen, die zur Orientierung dient, indem sie mit der Objektwelt in Übereinstimmung ist.
Ein rhythmisch sich wiederholender Algorithmus, der mir als mathematisches Modell für die Sinn- und Sprachproduktion vorschwebt, sollte demnach hauptsächlich Grenzen erzeugen, unzählig viele und komplizierte Grenzen, die alle innerhalb des Sinn-Ganzen miteinander verknüpft sind.
„Die Grenzen meiner Sprache bedeuten die Grenzen meiner Welt“, schrieb Ludwig Wittgenstein, und Wilhelm von Humboldt fasste den Gedanken in den Sätzen:
„Der Umfang des Wortes ist die Gränze, bis zu welcher die Sprache selbstthätig bildend ist“ und „Dies setzt natürlich eine große Schärfe der abgränzenden Beziehungen, da wir vorzüglich von diesen reden, aber auch eine gleiche in den Lauten voraus.“
Mit anderen Worten: Mit einer abgrenzend wirkenden Artikulation der Sprache werden Grenzen für die Bedeutung, den Umfang und den Sinn der Wörter und Sätze erzeugt, wird Verschiedenes unterschieden und entschieden. Ein Algorithmus der geistigen Tätigkeit muss in gleichförmiger Tätigkeit Grenzen erzeugen, wenn er Sinn und Sprache begreifbar machen soll.
Als weitere Forderung muss noch
- (IV) der Begriff Ähnlichkeit mit dem Konzept verbunden werden.
Um die Bedeutung von „Ähnlichkeit“ zu verstehen, erinnere ich an das „Höhlengleichnis“ des griechischen Philosophen Plato.
Plato beschrieb unsere eingeschränkte Fähigkeit zur Erkenntnis der Welt mit der Situation von Menschen, die in einer Höhle mit dem Gesicht zur Wand sitzen und auf der Wand nur die Schatten der Objekte wahrnehmen, die mit dem Licht vom Höhleneingang in die Höhle gelangen.
Das Höhlengleichnis ist ein schönes Bild, das die Bedeutung von Grenzen (Schatten) unterstützt und unser mangelhaftes Wissen entschuldigt, aber es bietet keine Erklärung dafür, warum die Menschen trotz behinderter Erkenntnismöglichkeit zu dem enormen Wissen gekommen sind, mit dem sie heute umgehen.
Diese Erklärung schaffen wir durch eine Erweiterung des Höhlengleichnisses mit Hilfe des Begriffes „Ähnlichkeit“:
Die Bewohner der Höhle sehen nur die Grenzen der Dinge, aber darin können sie Ähnlichkeiten entdecken und so zu einer Einteilung der Objekte und zum (eingeschränkten) Wissen über die Welt gelangen.
Die biologische Fähigkeit zum Entdecken von Ähnlichkeiten muss nicht weiter bewiesen werden, denn sie gehört mit Sicherheit zu den elementaren Qualitäten der Sinnesorgane im gesamten Tierreich.
- (V) Pars pro toto
Schließlich soll noch die sprachliche Komprimierung der ähnlichen Grenzgebilde durch das mathematische Modell anschaulich gemacht werden.
Diese komprimierte Form der Sinngrenzen in kurzen Folgen von Lauten oder Buchstaben lässt sich in vornehmem Latein als Pars-pro-toto-Funktion benennen, also: „Ein Teil steht für das Ganze“.
Was mit „Pars pro toto“ gemeint ist, lässt sich mit der Spurensuche erklären, die unsere Vorfahren bei der Jagd zur hohen Kunst entwickelt hatten.
Aus winzigen Fußspuren, abgeknickten Gräsern usw. können Jäger oder Detektive umfangreiche Zusammenhänge „lesen“. Heute genügen schon mikroskopische DNA-Spuren, um einen Täter zu identifizieren, ein Teil steht für das Ganze. Dass diese Fähigkeit nicht nur Menschen, sondern auch Hunden zu eigen ist, merkt ein Hundehalter oft, wenn er z.B. die Leine in die Hand nimmt, und der Hund schon zur Tür läuft, weil er die Bedeutung der Geste versteht, pars pro toto.
Zusammenfassend muss eine Vorschrift zur Erzeugung von Sinn und Sprache in schneller Taktfolge komplizierte Grenzen in organischem Zusammenhang produzieren, wobei eine Ähnlichkeit der Sinngrenzen einer Ähnlichkeit der Objektgrenzen entspricht. Die individuellen Grenzformen der Begriffsgestalten sind durch eine „Pars-pro-toto“-Funktion untrennbar mit kurzen Zeichenfolgen verbunden, die als Sprache funktionieren.
Mathematikstunde
Die Anforderungen, die an eine Bauanleitung für Sinn und Sprache zu stellen sind, erscheinen sehr schwierig zur Vorstellung oder Realisierung zu sein.
Als Wissenschaftler stellt man oft mit Staunen fest, dass die Natur sehr komplizierte Dinge mit sehr einfachen Mitteln herstellen kann. Sinn und Sprache sind die kompliziertesten Produkte der Natur. Es soll uns nicht wundern, wenn deren Rätsel auch eine sehr einfache und schöne Lösung erhält.
Es wurde schon erwähnt, dass die mathematische Sprachform besonders gut zur übersichtlichen Darstellung komplizierter Dinge geeignet ist.
Wir beginnen also eine kurze Mathematikstunde mit der Formulierung der Aufgabe, die in mathematischer Darstellung als Algorithmus gelöst werden soll:
Gesucht wird ein Algorithmus, der in rhythmischer Abfolge durch Grenzbildung ein lebendig wachsendes Sinnsystem erzeugen kann, in dem unendlich viele ähnliche und unterscheidbare Gestalten mit einer „Pars pro Toto“-Funktion durch kurze Zeichenfolgen repräsentiert werden können.
Algorithmische Grenzbildung
Die einfachste Form einer Grenze, zwei Grenzpunkte auf einer Linie, erhalten wir durch die ständige Abfolge einer sehr einfachen Vorschrift, der wiederholten Quadrierung (Iteration). Wenn der Ausgangswert, die Zahl, mit der ich die Quadrierung beginne, größer als Eins ist (>1) , dann werden alle folgenden Ergebnisse immer größer, sie gehen gegen Unendlich.
Beispiel: 2,4,16,..........
Umgekehrt werden die Ergebnisse immer kleiner und gehen gegen Null, wenn der Ausgangswert kleiner als Eins (<1) ist.
Nur mit der Eins kann der Vorgang beliebig oft wiederholt werden, das Ergebnis bleibt immer gleich Eins, die Eins ist ein somit Grenzpunkt auf der Zahlengeraden. Das Gleiche gilt auch, wenn ich das Vorzeichen 'Minus' benutze , für Minus-Eins.
Wir halten fest: Bei der iterierten Quadrierung der reelle Zahlen erhalten wir zwei Grenzpunkte, die wir uns auf der Zahlengeraden bei Eins und Minus-Eins vorstellen können.
Damit ist noch nicht viel erreicht, aber wir verstehen das nächste Grenz-Beispiel als Produkt wiederholter Quadrierung nun ohne große Schwierigkeit.
Verwenden wir bei der Quadrierung nicht reelle Zahlen, sondern komplexe Zahlen (mit einem imaginären und reellen Anteil), dann halten wir uns gedanklich nicht mehr auf einer geraden Linie auf, sondern in der zweidimensionalen (Gaußschen) komplexe Zahlenebene. Auch hier erzeugt die iterierte Quadrierung eine Grenze zwischen den (komplexen) Zahlen, deren Ergebnisse gegen Unendlich oder gegen Null gehen. Diese Grenze ist in der Gaußschen Zahlenebene ein Kreis mit dem Radius Eins.
So erhalten wir mit einer sehr einfachen, aber oft wiederholten Rechenvorschrift immerhin schon eine geschlossene Grenzlinie, die ein zweidimensionales Gebiet präzise begrenzt. Wir behalten diese einfach zu verstehende Tatsache als wichtiges Zwischenergebnis der Mathematikstunde fest, obwohl die Kreislinie beinahe das Gegenteil von dem ist, was gesucht wird.
Wir suchen ja ein sehr differenziertes Grenzsystem voller Information, und die Kreislinie ist eine Grenzlinie, die überall die gleiche, also fast gar keine Information enthält. Dafür kann sie schon viel Ähnlichkeit aufweisen, sie ähnelt sich an jeder Stelle.
Wenn die grenzbildende Wirkung der wiederholten Quadrierung mit realen und komplexen Zahlen so mit ein paar gedanklichen Zahlenexperimenten zu erklären war, können wir die Spur zu dem Algorithmus, der den gestellten Anforderungen genügt, mit einer Exkursion in die Geschichte der Mathematik weiter verfolgen.
Gaston Maurice Julia war ein französischer Mathematiker, der als Soldat im ersten Weltkrieg verwundet in einem Lager lag und sich dabei mit dem Gedanken beschäftigte, wie die Kreisgrenze bei der iterierten Quadrierung komplexer Zahlen sich verändert, wenn bei jedem Zwischenergebnis noch eine bestimmte (komplexe) Zahl addiert wird, bevor erneut quadriert wird.
G. Julia konnte noch keinen Computer für seine Gedanken benutzen, und so konnte er keine Antwort auf seine Frage finden, aber er äußerte bereits eine Ahnung, dass mit dieser Methode bizarre Veränderungen der kreisförmigen Grenze zu erwarten sind, die das Phänomen „Selbstähnlichkeit“ in vielen Größenordnungen erzeugen.
Die Arbeit, die G. Julia zu dieser Frage schrieb, wurde 1919 von der französischen Akademie ausgezeichnet, blieb dann aber ein halbes Jahrhundert völlig unbeachtet.
Der polnische Mathematiker Benoit Mandelbrot (*1924) zählt sicher zu den neugierigsten und verspieltesten Vertretern seiner Fachrichtung. Er stieß in den 60ziger Jahren auf Julias Arbeit. Da er zu dieser Zeit bei IBM an der Entwicklung der Computer arbeitete, konnte er Julias Gedanken am Computer experimentell untersuchen. Eher mit spielerischem Zufall als mit methodischer Suche entdeckte Mandelbrot dabei die Formel, die ihn berühmt machte und seinen Namen trägt, die Mandelbrot-Menge.
Diese Grenze in der Gausschen Zahlenebene, die auch den Kosenamen „Apfelmännchen“ erhielt, entsteht wie die Juliamengen aus der iterierten Quadrierung komplexer Zahlen mit Addition einer (komplexen) Zahl.
Genau gesagt ist die Mandelbrot-Menge die Grenze zwischen allen Julia-Mengen, die in sich zusammenhängend sind (deren Ergebnisse gegen Null gehen) und den Julia-Mengen, die nicht zusammenhängend sind (im Ergebnis gegen Unendlich gehen).
Der Rand dieser Figur, der mit der sehr einfachen Formel erzeugt wird, entsteht aus einer Kreisform durch fortwährend wiederkehrende, kleiner werdende Einbuchtungen, wie die glatte Haut eines Apfels, die immer mehr verschrumpelt. Durch diesen Vorgang wird die Grenze fraktal, selbstähnlich in verschiedenen Größenordnungen.
Die Grenze der Mandelbrot-Menge ist das komplizierteste Objekt der Mathematik, weil in ihr unendlich viele verschiedene Julia-Mengen enthalten sind. Man kann diese Struktur wie ein Bilderbuch mit unendlich vielen selbstähnlich verschachtelten Bildern betrachten.
Sogar eine der Sprache ähnliche „Pars pro Toto“-Funktion lässt sich in der Mandelbrot-Menge nachweisen: Welche der unendlichen Strukturen im aktuellen Rechenvorgang erzeugt wird, hängt nur von der Zahl C (C für Control) ab, die zum jeweiligen Quadrierungsergebnis addiert wird. Es besteht somit für jede spezifische Zahlenfolge von C ein spezifischer Ausschnitt der fraktalen Grenze, der von ihr erzeugt wird.
Die kurzen Zahlenfolgen bewirken hier also die Erzeugung riesiger selbstähnlicher Strukturkomplexe, vergleichbar den DNA-Sequenzen und den sprachlichen Zeichenfolgen. Damit erscheint die Mandelbrot-Menge als Modell für den Zusammenhang von Sinn und Sprache.
Liebe(r) Leser(in),
Sie haben soeben verfolgt, wie mit einigen Indizien der Algorithmus, der für unsere Sinn-und Sprachproduktion verantwortlich sein soll, als ein sehr einfaches und gleichzeitig sehr kompliziertes mathematisches Modell vorgeführt wurde, eine unendlich komplizierte Grenze mit „Pars pro Toto“-Funktion, Selbstähnlichkeit und organischem Zusammenhang, erzeugt mit der häufigen Wiederholung einer äußerst einfachen Rechenvorschrift.
Zum Glück sind wir hier mit den Links in der Lage, jeden Begriff ausführlich zu erklären. Meine Darstellung der Julia-und Mandelbrot-Formeln ist ehrlich gesagt laienhaft und oberflächlich, noch dazu ohne Bilder (muss noch nachgeholt werden). Es gibt darüber jede Menge Literatur, aber hier genügt Wiki allemal, um sich gut zu informieren.
Deshalb möchte ich an dieser Stelle eine Pause einlegen, in der jeder Leser sich ein wenig mit der Mandelbrot-Menge beschäftigen kann und meine Behauptung, dass diese als mathematisches Modell für unsere Sinn- und Sprachproduktion dienen kann, kritisch überprüfen kann.
Originelle Ideen entstehen bekanntlich oft aus der Verbindung von weit voneinander entfernten Tatsachen. Die Entfernung unserer geistigen Tätigkeit zur Mandelbrot-Menge erscheint auf den ersten Blick unüberbrückbar weit. Bei genauerem Hinsehen wird der Leser mir hoffentlich zustimmen, denn: „Pulchritudo splendor Veritas“, „Die Schönheit ist der Glanz der Wahrheit“.
Mandelbrot-Mengen
Mandelbrot-Menge oder Z n+1 = Z n2 + c
Einen Kontinent kann man allein durch Bilder schon kennen lernen, aber reichhaltiger sind die Eindrücke einer Reise.
Ähnlich ist es mit der MM (Abkürzung für Mandelbrot-Menge), die in vielen Ausschnitten in Wiki Commons unter Mathematik/ Fraktale/ Mandelbrot-set zu sehen ist.
Ein tieferes Verständnis ergibt sich mit jedem Computer, wenn darin ein kleines Programm (z. B. Winfrakt) aus dem Internet installiert wird, das die Figur selbst auf dem Bildschirm erzeugt. Wie mit einem Mikroskop kann man dabei Ausschnitte der Grenze vergrößern und wie auf einer Reise den unendlichen Formenreichtum erleben. Indem die Auswahl der Farben variiert wird, lassen sich unendlich viele schöne Bilder mit künstlerischem Reiz herstellen.
Zum philosophischen Staunen muss schon der extreme Kontrast zwischen den unendlichen Strukturen der MM und der simplen Formel ihrer Herstellung anregen.
Mit ihren Symmetrieeigenschaften, den Spiralen, Verästelungen und dem organischen Zusammenhang erinnert die MM auch an biologische Systeme, die ebenfalls aus kleinen Vorschriften äußerst komplexe Strukturen erzeugen.
Die Möglichkeit, die Ergebnisse dieses kurzen Algorithmus mit dem Computer sichtbar zu machen, ist auch hilfreich dabei, ihn als anschauliches Modell für Sinn und Sprache zu benutzen.
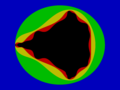
Betrachten wir die folgenden Bilder, auf denen die Ergebnisse der ersten Arbeitsschritte der Formel erkennbar sind.

Die erste Quadrierung erzeugt eine kreisförmige Grenze zwischen Blau und Schwarz, eine informationsarme Linie.
Wir können diese Grenze als Modell für den geistigen Zustand betrachten, den ein neugeborenes Kind am Beginn seiner geistigen Entwicklung hat, die berühmte „Tabula rasa“, noch völlig ohne Information.

Der zweite Iterationsschritt erscheint als symmetrische grüne Einbeulung, die zu einer Birnenform der Grenze führt..
Wenn wir darin ein Modell für die ersten Eindrücke sehen, die ein Baby erhält, kann auch wieder an die biblische Schöpfungsgeschichte erinnert werden.
Demnach entstand die Vielfältigkeit der Welt am Anfang aus groben, symmetrischen Einteilungen in Licht und Dunkel, Wasser und Land, Himmel und Erde usw.
Ähnlich muss das Neugeborene seine ersten Eindrücke in grobe Kategorien wie z. B. hell und dunkel, laut und still, warm und kalt usw. abgrenzen, wenn es sein eigenes Wissen von der Welt aufzubauen beginnt.

Der dritte Schritt macht mit neuen Dellen das Prinzip aller weiteren Schritte deutlich: Jede vorangegangene Einbuchtung wird durch zwei neue, kleinere Eindrücke verformt, wobei eine strenge Spiegelsymmetrie erhalten bleibt, aber eine Differenzierung der nun sich herausbildenden Längsachse bemerkbar ist.
Die Spitze im linken Teil der Längsachse steht als einziger Punkt noch mit dem ursprünglichen Kreis in Verbindung und wird es auch nach allen folgenden Arbeitsschritten des Algorithmus immer bleiben.
Die folgenden Schritte lassen das Prinzip immer klarer sichtbar werden: So wie man bei einem Menschenkind von seinen ersten Eindrücken spricht, die durch ständige Verfeinerung ein ständig sich differenzierendes Weltbild entstehen lassen, so entwickelt die Grenze der MM aus immer feiner werdenden Einbuchtungen einen kosmischen Formenreichtum in organischem Zusammenhang.
- 4.-30.Iteration
-
-
5.Schritt der MM
-
left
-
30. Schritt der MM
Die Bilder zeigen die ersten Wiederholungen eines endlos wiederholbaren Vorgangs. In den symmetrischen Umrissen der Grenzlinie wird schon eine „quasi natürliche“ Gestalt wie ein Käfer oder Blatt sichtbar. Es lässt sich auch erkennen, dass die Grenzlinie durch die neuen Eindrücke nie unterbrochen wird, also immer in ganzheitlichem Zusammenhang bleiben muss.
Bei dreißig Iterationen sind die neu hinzugefügten Einbuchtungen schon so klein, dass die Grenzveränderungen in der Grundfigur kaum noch erkennbar sind. Der Computer ermöglicht es aber, sehr kleine Ausschnitte wie mit einem Mikroskop zu betrachten.

Der Ausschnitt zeigt schon sehr deutlich die Selbstähnlichkeit der Grenze, die unendlich viele kleine Kopien der Grundfigur enthält. Auch die immer feiner werdende Verästelung der Grenze ist sichtbar, lässt aber nicht erahnen, welche unendlich feinen Strukturen noch darin verborgen sind.
Ich denke, dass mit diesen Bildern gezeigt werden kann, wie das mathematische Modell den Beginn des kindlichen Weltwissens und seine endlose Verfeinerung anschaulich machen kann.
Für ein Verständnis der sprachlichen Minimierung, zu dem die anfängliche Frage hinführen sollte, kann der C-Wert der Formel herangezogen werden. Das ist die (komplexe) Zahlenfolge, die jedem Teil der Grenze in der komplexen Ebene zugeordnet ist und diesen Teil konstruiert, wenn er in die Formel eingesetzt wird. Vergleichbar den Samen und den sprachlichen Zeichenfolgen ist auch der C-Wert eine kurze Zeichenfolge, die sehr komplexe Strukturen mit „pars pro toto“– Funktion erzeugen kann.
Um den Vorteil dieser Fähigkeit leicht zu begreifen, genügt wieder einmal der Vergleich mit der Digitaltechnik:
Jedes der obigen Bilder wird vom Computer aus 768x1024 Pixeln hergestellt und benötigt zur Speicherung 2,2 MB Speicherplatz. Um die Speichermenge zu verringern, lassen sich technische Algorithmen einsetzen, die „überflüssige Information“ heraussuchen und eine „abgespeckte Version“ erzeugen, die aber immer noch über 100 KB Speicher benötigen wird, um das Bild ohne bemerkbare Verluste zu rekonstruieren.
Wenn das Bild aber anstatt dessen als Ergebnis eines ständig wiederholten Algorithmus mit einem kurzen Controll-Wert C herstellbar ist, dann genügt es, diesen C-Wert zu speichern, um das Bild völlig verlustfrei wieder daraus zu rekonstruieren.
Es liegt auf der Hand, dass die Speicherung einer kurzen Zahlenfolge den Speicherbedarf extrem vermindert. Auch die Übertragungszeit hängt von der Größe einer Datei ab und wird durch die knappe Zeichenfolge so kurz, dass eine Kommunikation in „Echtzeit“ überhaupt erst möglich ist.
Zusammenfassend lässt sich sagen, dass die Visualisierung der MM am Computer wesentliche Aspekte von Sinn und Sprache anschaulich und begreifbar macht.
Wir haben damit ein Grundprinzip der sprachlichen Tätigkeit in einem sehr abstrakten, aber mit Hilfe des Computers sichtbar gemachten Algorithmus vor Augen. Das Prinzip besteht in der Sprache wie in der MM in einer Minimierung der unendlich komplexen Strukturen in kurze Folgen von Werten, die einen ständig wiederholenden Algorithmus steuern, der die Strukturen in einer organisch verbundenen Grenze rekonstruiert und das weitere Wachstum dieser Grenze modifiziert.
Das Modell bietet eine Erklärung für die nahezu unbegrenzte Speicherkapazität und die extrem schnelle Kommunikation der Menschen mit Hilfe der Sprache.
Ich will nicht verschweigen, dass diese Verbindung der geistigen Tätigkeit mit der Mandelbrot-Menge nicht über das rational-diskursive Denken hergestellt wurde, sondern mehr intuitiv mit einer unmittelbaren Einsicht begann, die mich durch ihre Einfachheit und Schönheit überzeugte...
Ich bin deshalb dankbar, hier die Möglichkeit zur komfortablen Darstellung mit Links und Bildern zu erhalten.
Hinweis:
Wer kein Programm zur Erzeugung der Mandelbrotmenge nutzen möchte, kann Videos im Internet dazu finden. Zum Beispiel dieses Video auf YouTube.
Na und?
Was ist gewonnen mit einer gedanklichen Verbindung zwischen dem „ungeheuren Gewebe“ der Sprache, „in dem jeder Theil mit dem anderen, und alle mit dem Ganzen in mehr oder weniger deutlich erkennbarem Zusammenhang stehen“ (Humboldt), und der fraktalen Grenzstruktur, die wir als Ergebnis der einfachen Rechenvorschrift Z n+1 = Z n² + c am Computer betrachten können?
Vorurteile
Bisher existiert noch kein wissenschaftliches Modell für jenes Phänomen, das wir subjektiv als „Sinn“ sehr gut kennen und zum sprachlichen Ausdruck bringen können. Wenn die Mandelbrot-Menge uns bei der Vorstellung hilft, wie dieses spezifisch menschliche „geistige“ Produkt aus geregelter Tätigkeit zu erklären ist, dann füllt sie nicht ein Vakuum, sondern muss sich gegen bestehende Vorurteile behaupten.
Über Jahrtausende herrschte im Kulturkreis der von Abraham und Moses gegründeten Religionen die Vorstellung, dass die Menschen die Sprache im Paradies von ihrem göttlichen Schöpfer erhielten und ihr Sinnverständnis durch den Genuss der verbotenen Frucht vom Baum der Erkenntnis geweckt wurde. Als Strafe für ihren babylonischen Hochmut verwirrte Gott die Menschen so, dass sie in verschiedenen Sprachen redeten und sich nicht mehr verständigen konnten.
Erst die Aufklärung brachte mit Herder, W. von Humboldt usw. die Idee von der natürlichen Evolution der Sprache und der geistigen Fähigkeiten in die Diskussion. Erst seit dieser Zeit gibt es eine akademische Sprachforschung. Die Linguistik ist im Vergleich zur Mathematik oder Musikwissenschaft eine junge Wissenschaft, noch in den Kinderschuhen.
„Ignorabimus“ (wir werden es nie wissen) war die Grundüberzeugung der Wissenschaftler bis zur Mitte des zwanzigsten Jahrhunderts, wenn es um eine genaue Erklärung des Bewusstseins und der geistigen Vorgänge ging. Erst mit der Simulation geistiger Vorgänge in den ersten Computern konnte die Natur der geistigen Vorgänge in neuem Licht gesehen werden und deren naturalistische Erklärung ins Auge gefasst werden. Mit dem Begriff „Künstliche Intelligenz“ versprach man sich auch ein neues Verständnis für die natürliche Intelligenz.
Durch die neue, technische Sichtweise kam ein neues Vorurteil in Mode, welches lautet: „Alle geistigen Vorgänge können auf digitale Rechenvorgänge zurückgeführt werden.“ Diese optimistische Meinung wird heute auch von der Neurophysiologie unterstützt, weil Nervenzellen tatsächlich ähnlich wie die Schaltelemente der Computer arbeiten, das heißt: Mit Nervenzellen lassen sich die logischen Grundfunktionen (und-oder) und Rechenoperationen ausführen.
Heute sind alle geistigen Produkte digitalisierbar, Text, Musik, Bilder, Videos, alles kann gespeichert, bearbeitet und im Internet sekundenschnell verschickt werden, und so sagt die gängige Meinung der technisch gebildeten Zeitgenossen heute oft, dass alle geistigen und auch sprachlichen Vorgänge auf digitaler Grundlage wie im Computer zu erklären sind.
Mit bescheidenen Errungenschaften, zum Beispiel den elektronischen Navigationshilfen im Auto und Robotern, die auf gesprochene Befehle reagieren, stützen Computerexperten ihre Hoffnung, eines Tages mit den Maschinen wie mit Menschen sprachlich zu kommunizieren. Elektronische Gesprächspartner oder Briefpartner sind bisher jedoch noch nicht möglich, keine Rechenmaschine versteht den Sinn der von ihr durchgeführten digitalen Operationen, kein Computer hat ein Wissen davon, was er tut, und kein Computer hat bisher den Turing-Test bestanden.
Sind neuronale Netze die Lösung?
Einen Ausweg aus dem Problem, menschliches Denken und Sprechen elektronisch zu simulieren, sehen die Fachleute in dem Terminus neuronale Netze, mit dem Gedächtnismodelle entwickelt wurden, wie sie auch in der Gehirnrinde vermutet werden.
Doch auch bei neuronalen Netzen fehlt der Qualitätssprung, der das menschliche Erleben von Sinn und das zu Grunde liegende Weltwissen hervorruft.
Über diesen Mangel der neuronalen Netze sehen die Fachleute hinweg, indem sie den Begriff einer parallelen Datenverarbeitung von der gewöhnlichen, seriellen Datenverarbeitung abgrenzen und in der „massiven Parallelverarbeitung des Gehirns“ das Geheimnis der menschlichen Geistestätigkeit vermuten. Mit einer milliardenfachen parallelen Verarbeitung soll erklärbar werden, warum der Mensch in einem Augenblick so viele Sinnesdaten gleichzeitig verarbeiten kann, wie es von keinem Computer zu schaffen ist.
Hier sollte bedacht werden, dass im Prinzip kein Unterschied zwischen einem parallelen und einem seriellen Computer besteht, beides sind letzten Endes Rechenmaschinen. Unterschiede können nur in der größeren Verarbeitungsgeschwindigkeit der parallelen Computer liegen, aber der Qualitätssprung zum Sinnverständnis und dem Wissen um das eigene Handeln ist mit diesem Schlagwort nicht erklärbar.
Parallelen sind dadurch definiert, dass sie einander nie berühren. Bei der augenblicklichen, sinnlichen Erfassung einer komplexen Situation sind jedoch alle Sinnesdaten in Verbindung und ergeben einen zusammenhängenden Sinn, der aus paralleler Datenverarbeitung per definitionem gar nicht gewonnen werden kann. Die Einheit des bewussten Erlebens scheint ganz unvereinbar mit dem Bild eines Parallelcomputers zu sein.
Ein weiteres Problem ergibt sich aus der Gestalt der neuronalen Netze, wie sie tatsächlich in der Hirnrinde existieren. Weder von der Neurophysiologie noch von der mathematisch-technischen Seite wurde die spezielle Art und Weise der Verästelung beachtet, die von den Nervenzellen im Großhirn ausgebildet wird.
Der Psychologe Donald Hebb, der die Idee der neuronalen Netze 1949 als Erster formulierte, konnte noch keine Angaben über die Feinstruktur der Verästelungen im Großhirn machen, weil die Architektur der Hirnrinde noch nicht restlos bekannt ist. Die Verbindungen der Nervenzellen sind im Cortex so komplex, dass ihre genaue Beschreibung bisher unmöglich ist.

Die Informationstheoretiker entwickelten technischen Nachbildungen der neuronalen Netze in geradlinig-geometrischen Formen. Diese technisch-geradlinige Form der Darstellung wurde von bekannten Hirnforschern, z. B. dem Nobelpreisträger John C. Eccles, auch für ein gedankliches Modell der Gedächtnisorganisation übernommen. Warum diese technisch-gradlinige Darstellung von neuronalen Netzen der Großhirnarchitektur in die Irre führt, kann mit folgenden Gedanken begründet werden:
In den technischen Schaltplänen werden die leitenden Verbindungen der Elemente völlig unabhängig von ihrem tatsächlichem Verlauf aus praktischen Gründen als gerade Linien mit rechtwinkeligen Abzweigungen eingezeichnet. Man kann diese idealisierende Abweichung vom realistischen Verlauf bei elektrischen Leitungen ohne Probleme im Schaltbild vernachlässigen.
Es ist aber eine Frage von grundlegender Bedeutung, ob solche Abweichungen von der Realität bei den neuronalen Verbindungen im Gehirn genauso ignoriert werden können, wie in den technischen Geräten. Dieses Problem ergibt sich nicht nur im Blick auf die Hirnrinde sondern stellt sich in allen Teilen des Gehirns.

Einer technisch-geradlinigen Modellierung der Neuronenverbände steht die Tatsache entgegen, dass die Nervenzellen für ihre vielseitigen Aufgaben im Nervensystem sehr unterschiedliche Formen der Verästelung ausbilden. Die Genetiker sprechen von omnipotenten Stammzellen, die je nach ihrem Einsatzort im Gehirn spezifische Formen ausbilden und sich danach mikroskopisch in ihren spezifischen Verästelungsformen gravierend unterscheiden, zum Beispiel als Purkinje-Zelle, Pyramidenzelle, Sternzelle, Golgi-Zelle, Mooszelle usw.
Die im Gehirn zu beobachtenden Verzweigungen der Nervenzellen unterliegen also weder dem Zufall noch folgen sie den geometrischen Mustern der technischen Nachbildung. Deshalb findet man im ganzen Nervensystem sehr charakteristische Formen der Verästelung, die jeweils einer spezifischen Funktion in einem speziellen Hirngebiet optimal angepasst sind.
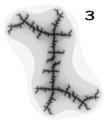
Als Beispiel für die Bedeutung der spezifischen Verästelung kann auf das Kleinhirn verwiesen werden, dessen Zellarchitektur gut bekannt ist. Hier sind es die sogenannten Purkinje-Zellen, die mit ihrer spalierartigen Verzweigung einzigartig im ganzen Nervensystem sind und in der Kleinhirnrinde eine ganz spezielle Aufgabe der zeitlichen Bewegungssteuerung erfüllen.
Es ist unwahrscheinlich, dass die Verzweigungsarchitektur im Großhirn dem Zufall überlassen ist. Eher ist zu vermuten, dass die Verzweigungen der dort vorherrschenden Pyramidenzellen genau wie die Verästelungstypen der übrigen Nervenzellen durch Wachstumsvorschriften geregelt werden, die zur Differenzierung ihrer Verästelung und damit auch ihrer Funktion führen.
Aus dieser Sicht erscheint das verbreitete Konzept der künstlichen „neuronalen Netze“ mit paralleler Verarbeitung mangelhaft, seine Misserfolge sind erklärbar.
Ein mathematisches Modell für das Sinn-Ganze
Als Alternative zu dem bekannten Modell (neuronale Netze im Parallelcomputer) hat der Mandelbrot-Algorithmus den Vorteil, dass seine fraktale Grenzstruktur sichtbar gemacht werden kann. Der unendliche Formenreichtum in ganzheitlichem Zusammenhang ermöglicht uns die Vorstellung, wie in unserem Kopf etwas Ähnliches, ein Sinn-Ganzes aus vielen kleinen Schritten aufgebaut werden kann.
Der sichtbare Zusammenhang verschiedener Strukturen mit bestimmten Zeichenfolgen (dem C-Wert) gestattet einen Vergleich mit der in Zeichenfolgen komprimierenden Fähigkeit der Sprache (und der Samen).
„Der Mensch berührt beim Sprechen, von welchen Beziehungen man ausgehen mag, immer nur einen abgesonderten Theil dieses Gewebes, thut dies aber instinktgemäß immer dergestalt, als wären ihm zugleich alle, mit welchen jener einzelne nothwendig in Übereinstimmung stehen muss, im gleichen Augenblick gegenwärtig.“ So beschrieb W. von Humboldt die Pars-pro-toto-Funktion der Sprache. Die Mandelbrot-Formel kann auch diese Funktion vor Augen führen, weil in jedem Teil ihrer Grenzstruktur eine kleine Kopie der Grundfigur gefunden werden kann, in jedem Teil das Ganze, wie die genetische Substanz in jeder Zelle eines Organismus.
Diese einmaligen Eigenschaften einer simplen Rechenvorschrift lassen die MM als nützliches Modell für Sinn und Sprachfunktion erscheinen.
Um nicht missverstanden zu werden: Wir behaupten damit nicht die völlige Übereinstimmung der Formel mit der Realität der Gehirnvorgänge, sondern möchten nur auf eine Ähnlichkeit der Eigenschaften hinweisen, die auf ähnliche Vorgänge ihrer Realisierung schließen lässt.
Mathematische Vorgänge können auf verschiedene Weise realisiert werden, in Nervensystemen oder elektronischen Schaltungen, und so kann das Modell uns hilfreich beim Verständnis unserer geistigen Vorgänge sein, aber auch als Anregung für zukünftige Computer dienen, die einmal den Turing-Test bestehen sollen.
Der Pulsschlag des Geistes
Plädoyer für das Einbeziehen der Hirnforschung
Sprache ist kein Produkt der Zunge sondern des Gehirns. Folglich ist die moderne Gehirnforschung zunehmend auch für die Linguistik und Philosophie von Interesse.
Der Sprachwissenschaftler Wolfgang Sucharowski schrieb in Sprache und Kognition (1996): „Nicht eine Theorie an sich kann das Erkenntnisziel sein, sondern eine Theorie über Sprache, die mit Erkenntnissen aus der psycho- und neurolinguistischen Forschung verträglich ist und insofern an solche Prozesse heranführt, die aufgrund der neurophysiologischen Disposition Sprache und Sprechen ermöglichen.“ Sucharowski geht davon aus, dass der vom Kognitionssystem des Menschen konstruierten Welt ein universales konzeptuelles System zugrunde liegt, „welches die Welt überhaupt erst erfahrbar macht und die Struktur der projizierten Welt organisiert.“ Dazu bemerkt er: „Konstitutiv für eine sprachpsychologische Erklärung ist eine theoretische Grundlegung der Zeitlichkeit einzelner Produktionsschritte“.
Sucharowskis Absichten verfolgend erinnere ich, was im Abschnitt „Am Anfang war der Rhythmus“ resümiert wurde: „Halten wir fest, dass es zahlreiche Hinweise für einen Arbeitstakt der geistigen Tätigkeit gibt, also des gesuchten Algorithmus, der Sinn und Sprache erzeugt.“
Dieser Gedanke kann weitergeführt als Brücke in die Neurophysiologie des Organs führen, in dem die geistige Tätigkeit stattfindet; zu den messbaren Vorgängen des lebendigen Gehirns.
Jeder Algorithmus, der sich in einer Schleife endlos wiederholt, erzeugt mit seiner regelmäßigen Abfolge auch einen Rhythmus.
Umgekehrt kann man immer dort, wo man einen Rhythmus entdeckt, einen Algorithmus dahinter vermuten, denn jede regelmäßige Erscheinung folgt einem Gesetz, dass mathematisch formuliert werden kann.
Das Organ, in dem Sinn und Sprache fortwährend erzeugt werden, ist die Großhirnrinde. Beim Schlaganfall kommt es oft zum Sprachverlust, weil der für die Sprache wichtigste Teil der Hirnrinde zerstört wurde. Die Betroffenen können aber immer noch Sinn verstehen, sinnvoll handeln, weil die andere Hälfte des Gehirns noch arbeitet. Auch das ist nicht mehr möglich, wenn durch Narkose oder Gifte die Großhirnrinde völlig lahmgelegt wird und das Bewusstsein entschwindet.
Die Frage kann also sein, ob in der lebenden Großhirnrinde ein Rhythmus zu finden ist, der als Hinweis für die Iteration eines Algorithmus dienen kann?
Zum Vergleich: In der Brust schlägt, von außen kaum zu bemerken, eine rhythmische Aktivität des Herzens, die nach einem genauen Schema von den Vorhöfen beginnend durch den Herzmuskel verläuft.
„Gibt es auch einen Pulsschlag des Geistes?“ ist eine Frage, die an die Hirnforschung gerichtet ist.
Die Gehirnwellen

Heute gehört es schon zum Allgemeinwissen, dass im Gehirn Wellen gemessen und aufgezeichnet werden können, deren prominenteste Erscheinung die Alphawellen sind, die 1929 von dem Arzt Hans Berger in Jena erstmalig aufgezeichnet (Elektoencephalographie, EEG) und veröffentlicht wurden. Inzwischen haben unzählige Untersuchungen mit verfeinerter Technik ein breites Spektrum dieser typischen Spannungsschwankungen in der Großhirnrinde nachgewiesen, das EEG ist wie das EKG eine ärztliche Standarduntersuchung und Wissenschaft für sich geworden.
Lange bekannt ist der Zusammenhang der Hirnwellenfrequenz mit dem Grad der Wachheit (Vigilance) des Subjekts. Die schnellsten Wellen bis 40 Hz treten bei offenen Augen und geistiger Anspannung vorwiegend im visuellen Cortex auf.
In der entspannten Laborsituation findet man bei offenen Augen oder geistigen Aufgaben im EEG überwiegend Betawellen (13-30 Hz) mit der Tendenz zur Desynchronisation.
Bei geschlossenen Augen und ruhendem Geist sind über der ganzen Hirnrinde nur noch acht bis zwölf synchrone Schwankungen (Alphawellen) zu registrieren, die beim Öffnen der Augen oder beim Lösen einer Rechenaufgabe sofort wieder in die schnelleren Betawellen (16-30Hz) übergehen. Wenn die Person einschläft oder in Narkose versetzt wird, werden die Wellen langsamer, weniger als sechs pro Sekunde (Deltawellen). In den Traumphasen, die sich durch schnelle Augenbewegungen (REM-Schlaf) feststellen lassen, treten jedoch wieder Alphawellen auf.
Die Bedeutung, die heute den Hirnwellen beigemessen wird, lässt sich daran erkennen, dass als moderne Definition des Todes einer Person nicht deren Herzstillstand, sondern die Null-Linie im EEG, der Hirntod, international festgelegt wurde.
Obwohl schon Hans Berger einen Zusammenhang der Alphawellen mit der „psychischen Energie“ nachweisen wollte, sind neben dem Wachheitsgrad, der Aufmerksamkeitsverteilung und einer bioelektrischen Beteiligung bei der Wahrnehmung (evoced Potentials) und der Handlungsvorbereitung (Bereitschaftspotential) bisher keine psychisch-geistigen Funktionen mit der Hirnwellentätigkeit in Verbindung gebracht worden, schon gar nicht die Sinnbildung oder sprachliche Funktionen.
Während der Rhythmus des Herzens und seine elektrische Aufzeichnung im EKG gut mit dem Wissen von der Funktion des Herzens in Einklang gebracht werden können, ist der im EEG aufgezeichnete Rhythmus der Großhirnrinde immer noch erklärungsbedürftig im Hinblick auf seine Beteiligung an den geistigen Vorgängen.
- Was bewirken die schnellen Spannungsschwankungen in der Großhirnrinde, und warum treten sie oft über der ganzen Hirnrinde synchronisiert auf?
- Was bewirken die unterschiedlichen Frequenzen in der Hirnrinde, wenn sie vom Schlaf bis zur angespannten Aufmerksamkeit schneller werden?
- Warum sind die Wellen in den Traumphasen genau so schnell, wie im Wachzustand?
Der Arbeitstakt des Gehirns
Solche spekulativen Fragen sind in den medizinischen EEG- Laboratorien unbeliebt und werden dort gar nicht erst gestellt, aber ein Mathematiker mit ausgeprägtem philosophischen Interesse, der Vater der Kybernetik Norbert Wiener, schrieb schon 1948 in seinem Bestseller „Kybernetik“:
- ...“dass der weitverzweigte Synchronismus in verschiedenen Teilen des Cortex vermuten lässt, dass er von irgendeinem zentralen „Uhrwerk“ angetrieben wird. Wir können vermuten, dass dieser Alpharhythmus mit der Formwahrnehmung verbunden ist und dass er etwas mit der Natur eines Abtastrhythmus zu tun hat, wie der Rhythmus beim Abtastprozess eines Fernsehapparates (S.177).
Zu ähnlichen Ansichten kam der Physiker Dean Wooldridge in dem Buch „The Machinery of the Brain“ (1967), als er schrieb:
- „Die im EEG erzeugten Dendritenspannungen sind für gewöhnlich zu klein, um die Neurone zu ihrer charakteristischen Impulsabgabe zu veranlassen. Dennoch hat das Auf und Ab der Dendritenspannungen wahrscheinlich ein entsprechendes Auf und Ab der Bereitschaft zur Folge, mit der die Neurone auf den Empfang der spezifischen Impulsarten von anderen Neuronen reagieren. Mit anderen Worten , der Alpharhythmus dürfte die Ausbreitung einer periodischen Sensibilisierungswelle über alle Neurone anzeigen.“
Wooldridge zog ähnliche Parallelen wie Wiener:
- „Diese Interpretation des Alpharhythmus erinnert an die Zeitgeber, die man zur Synchronisation von Digitalrechnern verwendet. Das Ergebnis ist in beiden Fällen, dass die vielen Einzelteile des Systems nur in diskreten, periodischen Zeitintervallen sensitiviert und arbeitsbereit sind“ (S. 132).
Der Mathematiker und der Physiker, beide brachten vor Jahrzehnten einen fruchtbaren Gedanken aus dem Vergleich der elektrischen Hirntätigkeit mit der Rechenmaschine und dem Fernsehapparat in die Diskussion, die hier weitergeführt werden soll.
Heute sprechen schon Kinder von der Taktfrequenz ihrer Computer, die nicht hoch genug sein kann, damit die neuesten Spiele einwandfrei laufen.
Beweise für die Arbeitstakttheorie
Der Rhythmus der Gehirnwellen ist dagegen extrem langsam, und dennoch können die Menschen viele Leistungen schneller als die besten Computer, zum Beispiel das sofortige Erkennen von Gesichtern oder die sensomotorischen Leistungen beim Tischtennis. Wie ist dieser Widerspruch aufzulösen?
Wir halten den Vergleich mit dem Computer aufrecht, wenn wir diesem Problem nachgehen und zunächst mit einer einfachen Berechnung beweisen, dass die langsame Frequenz der Hirnwellen sich beim Menschen notwendigerweise aus seiner Körpergröße und der Nervenleitgeschwindigkeit ergibt. Dazu gehen wir von der Annahme aus, dass die Taktfrequenz in einem System durch die längsten Wege innerhalb des Systems begrenzt wird, weil eine Taktperiode nicht schneller sein darf als die Zeit, die für den längsten Weg von ihr benötigt wird.
Vom Kopf bis zum großen Zeh sind circa zwei Meter Nervenleitung die längste Wegstrecke im System Mensch. Weil die Nervenleitung bei maximal hundert Metern pro Sekunde mindestens 0,02 Sekunden für zwei Meter braucht und noch Verzögerungen in synaptischen Übertragungen dazugerechnet werden können, muss der Arbeitstakt in einem datenverarbeitenden System Mensch deutlich unter 50 Hz liegen, um vom Kopf bis zu den Füßen wirksam zu sein.
Einen Beweis für die Annahme, dass die Körpergröße des Organismus die Taktfrequenz seines Nervensystems begrenzt, findet man im Tierreich: Giraffen, Wale und Elefanten haben langsamere Bewegungen als Stichlinge oder Hunde, Mäuse und Wiesel sind sehr flink auf ihren kurzen Beinen, weil sie einen sehr schnellen Rhythmus haben, der Kolibri hat den schnellsten Flügelschlag unter den Vögeln, das Albatros den langsamsten. Insekten zeigen die Abhängigkeit ihrer Taktfrequenz von der Körpergröße mit der Tonhöhe ihrer Fluggeräusche, vom tiefen Brummen der großen Hummel bis zum hohen Schwirren der kleinen Mücke, dazwischen Biene und Fliege. Die Fruchtfliegen haben über 300 Flügelschläge pro Sekunde.
Bei Menschen gibt es auch kleinere und größere Individuen, und bei den Kleinen hat man oft den Eindruck, dass sie als Ausgleich etwas flinker sind als die Großen. Bei Spitzensportlern können solche feinen Unterschiede sich bemerkbar machen, und tatsächlich sind beim schnellsten Reaktionssport, dem Tischtennis, die besten Spieler immer deutlich unter 180cm, überwiegend Chinesen von relativ kleinem Wuchs. Die Großen sammeln ihre Erfolge dafür beim Basketball.
Aus diesen Beobachtungen lässt sich schließen, dass der im Vergleich zum Computer extrem langsame Rhythmus der Hirnwellen dem menschlichen Organismus als Arbeitstakt der Datenverarbeitung wahrscheinlich optimal angepaßt ist.
Ein Arbeitstakt im Gehirn, von dem wir nichts bemerken? Das kann bei vielen Lesern zum „Stirnrunzeln“ führen.
Um die Annahme zu prüfen, nehmen wir einmal das Gegenteil an, also dass es keine periodischen Sensibilisierungswellen in den Neuronen der Großhirnrinde gäbe, welche die Nervenzellen nur in diskreten, periodischen Zeitintervallen sensitivieren und arbeitsbereit machen, so wie es von D. Wooldridge und N. Wiener vorgedacht wurde.
Dabei wäre zu berücksichtigen, dass in der Hirnrinde jede Pyramidenzelle mit tausenden Verästelungen über alle Teile des Cortex in Verbindung mit anderen gleichartigen Zellen steht, die wiederum tausendfache Verbindungen haben. Wenn jede Pyramidenzelle zu jeder Zeit erregbar wäre, dann würde ein einziger Nervenimpuls genügen, um sich schnell wie ein Buschfeuer auf alle Zellen des Gehirns auszubreiten. Eine Verarbeitung nachfolgender Erregungen wäre unter diesen Umständen nicht mehr möglich.
Das Nervensystem verfügt aber nicht nur über die Möglichkeit der Erregung, sondern auch der Hemmung. Jede Nervenzelle kann zur Bildung von Impulsen angeregt oder auch daran gehindert werden. Mit dieser Fähigkeit lässt sich eine unkontrollierte Ausbreitung von Erregungen optimal durch einen Rhythmus verhindern, mit dem alle Zellen synchron abwechselnd in einen erregbaren oder unerregbaren Zustand versetzt werden.
Während in den gehemmten Phasen alle Nervenaktivität unterdrückt wird, können die Zellen in den erregbaren Phasen genau im gleichen Augenblick, sehr dicht an ihrer „Zündspannung“, gemeinsame Erregungskomplexe bilden. Das Ergebnis ist dann ein rhythmisch wechselndes Muster von Erregungszuständen, in dem die augenblicklichen Informationen des ganzen Systems enthalten sind.
Fazit: Der periodisch hemmende Arbeitstakt verhindert den Kollaps des Systems und macht aus dem verfilzten Nervenzellen-Teppich einen Mustergenerator für neuronale Netze, ein Organ der Orientierung.
Hebbs Gedächtniskonzept mit neuronalen Netzen wird durch eine periodische Arbeit der Hirnrinde nicht in Frage gestellt, sondern eher erst dadurch ermöglicht, wenn die Neuronen nur in kurzen Momenten synchron feuern können. Dann können sie nach dem Modell der Hebb´schen Synapsen ihre spezifischen Verbindungen knüpfen und ganzheitlich zusammenhängende Muster wachsen lassen, die sich in jeder Sekunde mehrfach erneuern, damit immer die aktuelle Situation abbilden und gleichzeitig in das Wachstum von Gedächtnisspuren umgesetzt werden. Vermutlich werden die Eigenschaften der neuronalen Netze, die von den Nervenzellen in der Hirnrinde gebildet werden, auch von der Art der Verästelung geprägt sein, die speziell von den Pyramidenzellen ausgebildet wird.
Wenn hier die Ausbildung einer fraktalen Grenzstruktur nach dem Vorbild der Mandelbrotmenge vermutet wird, dann wurden dafür schon Argumente genannt, die in den gemeinsamen Eigenschaften der Mandelbrotmenge mit dem Sinn-Ganzen und seiner sprachlichen Auslegung begründet liegen.
Eine haargenaue Beschreibung der corticalen Verästelungen erscheint fast unmöglich. Unter Beachtung der spezifischen, wurzelartigen Verästelungsformen von Pyramidenzellen lässt sich aber eine fraktale Geometrie ihrer Verbindungen annehmen, die in ihren Wachstumsvorschriften, den Genen, verankert ist, und ihren neuronalen Netzen fraktale Eigenschaften verleiht.
Der Rhythmus der Gehirnwellen kann demnach als Arbeitstakt für einen Algorithmus gesehen werden, der mehrmals in einer Sekunde die Pyramidenzellen synchron empfindlich für eintreffende Signale macht. Gleichzeitig erregte Zellen bekommen mit jeder gemeinsamen Erregung einen Impuls, sich mit neuen synaptischen Kontakten zu vernetzen. Die Verästelungen der Dendriten erhalten durch genetische Information eine fraktale Geometrie.
Das Ergebnis der rhythmischen Aktivität ist dann ein ganzheitlich verbundenes fraktales Netzwerk, in dem alle früheren Erregungsmuster schon Spuren in Form von gewachsenen Verbindungen hinterlassen haben, wie in unserem Gedächtnis.
Zugegeben, so ein Arbeitstakt im Großhirn ist nicht leicht vorstellbar. Das ganze Gehirn ist schwer durchschaubar und außer den EEG-Wellen haben wir bisher keinerlei Hinweise für eine rhythmische Aktivität der Hirnrinde. Vor allem bemerken wir selbst nichts von einem derartigen „Pulsschlag des Geistes“, denn unser Bewusstseinsstrom erscheint als ein ununterbrochenes Kontinuum ohne einen bemerkbaren Rhythmus.
Rhythmus in der Wahrnehmung
Um dennoch eine Vorstellung von der Existenz eines geistigen Rhythmus zu erhalten, erinnern wir uns an ein bekanntes Phänomen im Kino: Dort werden 25 Bilder pro Sekunde vorgeführt, aber wir erleben dabei nicht die einzelnen Bilder, sondern ein kontinuierliches Geschehen wie in der Realität. Das gleiche passiert beim Fernsehen nur mit einem kleinen Lichtpunkt, der in einer Sekunde zeilenweise 25 mal über den ganzen Bildschirm huscht. Unser Gehirn erkennt niemals den schnellen Lichtpunkt sondern erzeugt daraus lebendig zusammenhängende Bilderfolgen.
Bemerkenswert ist dabei, dass diese visuelle Verschmelzung genau bei den Frequenzen beginnt, die im EEG bei offenen Augen registriert werden, nämlich im Bereich der Beta-Wellen.
Unter der Annahme eines geistigen Arbeitstaktes kann man sich vorstellen, dass ein kontinuierlicher Eindruck immer dann entstehen muss, wenn jede sensible Periode des Gehirns ein ähnliches Bild erhält. Die dazwischen liegenden unerregbaren Phasen der Hirntätigkeit überbrücken dann die dunklen Intervalle der Kinovorführung, und aus einzelnen Bildern entsteht subjektiv ein zusammenhängender, lebendiger Eindruck.
Das gleiche Verschmelzungsphänomen begegnet uns beim Hören von Luftdruckwellen. Ab circa 18 Wellen pro Sekunde hören wir nicht mehr einzelne Wellen, sondern ein zusammenhängendes tiefes Brummen, einen Ton. Wenn die Wellen schneller werden, verändert sich der kontinuierliche Klang in der Art, dass wir sagen: Der Ton wird „höher“ korrekt wäre „schneller“).
Für die Ähnlichkeit der Verschmelzungsfrequenzen im optischen und akustischen Kanal bietet nur der Arbeitstakt der Hirnrinde eine plausible Erklärung.
Wenn die Vorstellung eines „geistigen Pulses“, der sich in den Hirnwellen und der Verschmelzungsfrequenz der Wahrnehmungen äußert, auch auf die Handlungen ausgedehnt wird, dann müsst sich sein Wirken auch in den schnellsten Bewegungen als Begrenzung zeigen.
Rhythmus in Handlungen
Der schnellste Rhythmus, den ein Mensch bewusst erzeugen kann, ist der Trommelwirbel. Sein Rhythmus kann durch jahrelanges Training bis auf ca. 16 Schläge pro Sekunde gesteigert werden, hier ist für alle Schlagzeuger eine unüberwindbare Grenze. Trillernde Musiker erzeugen maximal zwölf Perioden pro Sekunde, aber auch nur durch spezielle Übungen. Der Weltmeister auf der Schreibmaschine bringt es auf maximal zehn Anschläge pro Sekunde. Untrainierte Menschen sind deutlich langsamer, genau gesagt nur etwa halb so schnell. Fünf bis sechs mal pro Sekunde können wir mit dem Finger auf die Tischplatte klopfen, fünf bis sechs sprachliche Artikulationen sind in einer Sekunde möglich, und in der Musik sind die schnellen Sechzehntelnoten ungefähr in diesem Tempobereich zu spielen.
Bei den letzten olympischen Spielen wurde der 100-Meter-Lauf im Fernsehen in Zeitlupe vorgeführt, was eine Gelegenheit zum Zählen der Schritte ergab. Alle Läufer hatten genau die gleiche Schrittzahl, in den zehn Sekunden machten sie genau 50 Schritte, also zwei Meter mit jedem Schritt, fünf Schritte pro Sekunde.
Grob gesagt kann man also die schnellen Bewegungsrhythmen im Verhältnis zu den Hirnwellen nur halb so schnell ausführen. Daraus könnte ein Kritiker den Schluss ziehen, dass der Zusammenhang mit den Hirnwellen nicht ersichtlich ist. Man kann aber auch in dem Verhältnis 1:2 ein harmonisches Verhältnis erkennen und darin einen Hinweis für einen gesetzmäßigen Zusammenhang vermuten.
Dieser Zusammenhang kann in einer Handlungskontrolle bestehen.
Rhythmus in der sensomotorischen Kontrolle
Jede Handlung, die wir gezielt ausführen, bedarf einer ständigen (sensomotorischen) Kontrolle, um das Ziel optimal zu erreichen. Denken wir an Ballspiele, das Radfahren oder das Fangen einer Frisbyscheibe, dann sind diese Tätigkeiten nur denkbar mit einer Kontrollinstanz, die jeden Handlungsschritt überwacht und jederzeit Korrekturen der Handlungen einleiten kann. Schon das normale Laufen und Stehen auf zwei Beinen ist unmöglich ohne eine dauernde Kontrolle durch das Gleichgewichtsorgan, die uns gar nicht bewusst ist. Bewusste Kontrolle herrscht beim Sprechen, bei dem wir uns gleichzeitig auch zuhören und sofort jeden Versprecher korrigieren können.
In einem taktweise arbeitenden System kann der enge zeitliche Zusammenhang zwischen Handlung und Erfolgskontrolle sehr einfach dadurch hergestellt werden, dass auf jeden Handlungsschritt ein Kontrollschritt folgt, der korrigierend auf den nächsten Handlungsschritt wirkt, dem wiederum ein Kontrollschritt folgt und so weiter. So kann sich ein dynamisches System in periodischem Wechsel optimal an eine dynamische Umwelt anpassen.
Der technisch gebildete Leser erkennt in einer rhythmischen Folge von Handlung und Kontrolle ein einfaches Modell von Rückkopplung, die als grundsätzliches Merkmal von zielgerichteten Vorgängen in der belebten Natur und in der Technik gilt. Er kann damit auch verstehen, warum die schnellsten Bewegungen nur halb so schnell wie der Arbeitstakt sind, wenn nach jedem Bewegungsimpuls eine Kontrollphase folgen muss.
Die langsameren Rhythmen, die bei vielen Arbeitsvorgängen (Hämmern, Rudern) zu beobachten sind, verhalten sich zum schnellsten Rhythmus ebenso harmonisch, wie die Einteilungen des musikalischen Rhythmus in sechzehntel-, achtel-, viertel-, halbe- und ganze Noten, also mit Verdoppelung der Zeitwerte . Deutlich wird dieser harmonische Zusammenhang in den Liedern, die bei rhythmischen Arbeiten entstanden sind, beim Gleisbau, Spinnen, Marschieren, Treideln usw. Beim Wandern kann man eine synchronisierte Tätigkeit von Bein- und Atembewegungen feststellen, wobei z.B. auf vier Schritte ein Atemzug kommt.
Biologische und technische Taktfrequenz
Auf eine Besonderheit des biologischen Arbeitstaktes gegenüber technischen Vergleichen kann noch eingegangen werden:
In den Computern ist der Arbeitstakt nicht variabel, sondern er wird sehr exakt durch einen elektrischen Schwingkreis erzeugt, so schnell wie möglich und mit größter Präzision, genau wie die „Unruhe“ einer Uhr.
Der Rhythmus der Gehirnwellen und der Rhythmus unserer Bewegungen ist dagegen nicht auf eine exakte Frequenz beschränkt, er ist bis zu einer messbaren Grenze stufenlos variabel, wie es im EEG zu sehen und in der Musik zu hören ist.
Sicher ist die Erzeugung einer starren Frequenz ein technisch einfacher Vorgang, verglichen mit der Erzeugung einer in Grenzen variablen Taktfrequenz. Einfache Lebewesen haben oft sehr starre Bewegungsrhythmen, die nicht veränderbar erscheinen, z.B. die Kriechbewegungen von Würmern, die Kontraktionen der Quallen, das Zirpen der Zikaden. Im Lauf der Evolution zeigte sich die Fähigkeit zur Variation der Gangart natürlich als Vorteil und etablierte in den Gehirnen der höheren Tiere Taktgeber mit variabler Frequenz, welche Bewegungen in beliebigen Variationen vom Bummeltempo bis zur schnellen Fluchtreaktion gestatteten.
Damit soll gesagt sein, dass ein variabler „Hirnschrittmacher“ keine neue Errungenschaft der Menschen ist, sondern allen Säugetieren gemeinsam und in jedem Säugetierhirn nachweisbar ist.
Ein deutlicher Beweis für die Existenz einer variablen Taktfrequenz im Gehirn ist der Schlaf, der immer von einem stark verlangsamten Rhythmus der Hirnwellen begleitet ist. Wir können uns vorstellen, dass die Pyramidenzellen durch den langsamen Rhythmus unempfindlicher für Erregungen werden, kaum noch an ihre „Zündschwelle“ kommen und deshalb nur noch auf stark überschwellige „Weckreize“ reagieren.
Dahinter steckt ökonomischer Sinn. Die Pyramidenzellen verbrauchen sehr viel Energie bei ihrer Arbeit. In Ruhephasen können sie nicht ausgeschaltet werden wie ein Computer, aber ihr Energiebedarf wird stark gedrosselt, wenn sie durch einen langsamen Rhythmus unempfindlicher gemacht werden. Beim Menschen und allen Säugetieren wird der Energieverbrauch im Schlaf deshalb stark herabgesetzt.
Die Hirnstruktur, welche den variablen Pulsschlag des Geistes für die Gehirnrinde erzeugt, ist bekannt, sie wird „aufsteigendes Aktivierungssystem“ (ARAS) oder „Schlaf-Wach-System“ genannt und gehört zur Formatio reticularis des Hirnstamms.
Die Korrelationstheorie der Hirnforschung
Oben wurde bereits beschrieben, dass die ersten theoretischen Vorstellungen über eine rhythmische Tätigkeit des Gehirns schon vor circa 50 Jahren, am Beginn des Computerzeitalters, von dem Mathematiker Norbert Wiener und dem Physiker Dean Wooldridge veröffentlicht wurden.
In der Hirnforschung kam dieser Gedanke 1981 wieder durch den Physiker Christoph von der Malsburg – heute Professor an der Ruhr-Universität Bochum, in die Diskussion. In seiner „Korrelationstheorie der Hirnfunktion“ beschrieb v.d. Malsburg die zeitliche Verknüpfung von Nervenzell-Verbänden, das Bindungsproblem der Hirnforscher, als Ergebnis einer rhythmischen Hirnaktivität.
Wolf Singer, Direktor am Max Planck-Institut für Hirnforschung in Frankfurt a.M. und eine wachsende Zahl weiterer Wissenschaftler (Andreas Engel, Christof Koch, Rodolfo Llinas) bestätigten in folgenden Jahren die Existenz zeitlich synchronisierter Entladungen von neuronalen Ensembles in tierischen und menschlichen Gehirnen.
Mit vielen Untersuchungen konnte der Psychologe Ernst Pöppel, München, die theoretischen und neurophysiologischen Ergebnisse dieser Theorie untermauern und ihre psychologischen Konsequenzen formulieren. E. Pöppel geht davon aus, dass eine synchronisierende Aktivität von Nervenzellen die notwendige Bedingung für Entscheidungen und für die Identifikation von Ereignissen ist und auch dafür sorgt, dass wir Bewegungen in einem regelmäßigen Tempo ablaufen lassen können, also mit gleichbleibendem Tempo sprechen, gehen und auch musizieren können. Neuronale Oszillationen bezeichnet er als das Grundgerüst einer zeitlichen Koordinierung, eines inneren Fahrplans. Die Zeit wird nach Pöppel durch das Gehirn für uns überhaupt erst hergestellt in rhythmischen „Zeitquanten“, deren Periode ca. 30msec dauert, aber in gewissen Grenzen variabel ist.
„Synchronizität erzeugt Ganzheit“ ist der Grundsatz, unter dem der Philosoph Thomas Metzinger die Korrelationstheorie mit der Grundfrage der Philosophie (nach dem Verhältnis von Geist und Materie) in Verbindung bringt. In dem Aufsatz „Ganzheit, Homogenität und Zeitkodierung“ machte er folgende Grundannahme: „Die im Rahmen der Korrelationstheorie postulierte Form der Zeitkodierung ist der allgemeine Integrationsmechanismus, mit dessen Hilfe - zumindestens bei Systemen unseres eigenen Typs - alle Formen repräsentionaler Ganzheit generiert werden.“ Warum diese theoretische Annahme für eine philosophische Theorie des Geistes interessant ist, erklärte Metzinger so: „Wenn wir ein begrifflich konsistentes und auch empirisch nicht unplausibles Modell der Eigenschaftsbindung, also der Bildung von repräsentationalen Objekten als einer Form der Selbstorganisation besitzen, dann verfügen wir nämlich über die ersten Bausteine für eine naturalistische Theorie des Bewusstseins - also: für eine Erklärung von unten“.
Welcher Art dieses Modell sein sollte, präzisiert Metzinger: „Was wir eigentlich benötigen, ist ein mathematisches Modell, das auf präzise und empirisch plausible Weise die phänomenale Ontologie des menschlichen Gehirns beschreibt-also das, was es dem bewussten Erleben nach in der Welt gibt“.
Wir können also mit Metzinger, Pöppel und allen Anhängern der „Korrelationstheorie“ annehmen, dass die subjektive Zeit diskontinuierlich abläuft, dass der Ablauf unseres Erlebens und Verhaltens zerhackt ist in Zeitquanten von wechselnder Frequenz (zwischen circa 8 - 30 Perioden pro Sekunde). Die wiederholte Gleichzeitigkeit beziehungsweise die gleichartige Zeitfolge von Reizmustern verschiedener Herkunft ist für das Gehirn die Basis für die Fixierung neuronal übergreifender Strukturen, die in den „Zeitfenstern“ zu Einheiten verschmelzen. Die subjektive Empfindung eines kontinuierlichen Zeitstroms ist demnach eine Illusion, die sich aus der Verknüpfung aufeinander folgender „Augenblicke“ ergibt.
Die Vorstellung einer periodisch gequantelten Bewusstseinstätigkeit wird manchen Menschen schwer fallen, weil man nichts davon bemerken kann.
Umso mehr Bewunderung verdient der Berliner Arzt Carl Ludwig Schleich, der die Erkenntnis einer periodischen geistigen Tätigkeit schon vor 85 Jahren in seinem Buch „Bewußtsein und Unsterblichkeit“ (Rowohlt-Verlag) beschrieb: „Das Ich blitzt von neuem auf in jeder Sekunde. Es ist also etwas, was immer im Augenblick neu entsteht, und ist nichts Kontinuierliches. Es scheint uns nur deshalb kontinuierlich, dauernd vorhanden, eine Kette von Zuständen, das Gefühl eines Beständigen, eines dauernden Seins, weil diese Phase des Aufblitzens der Sternschnuppen von der bewussten und der unbewussten Welle immer wieder von neuem aufspringt und Blitz auf Blitz folgt, so schnell hintereinander aufzuckt, dass eben für uns die Täuschung einer Dauer und eines Zustandsverweilens entsteht.“(S.48)
Es sind immer noch nicht viele Wissenschaftler, die in den Hirnwellen einen Schlüssel zum Verständnis der Arbeitsweise der Großhirnrinde bzw. des Bewusstseins sehen, und ihre Folgerungen sind noch sehr vorsichtig und vage gehalten.
Unsere Vorstellung der rhythmischen Arbeitsweise kam ausgehend von der komprimierenden Funktion der Sprache über die Annahme eines iterierenden Algorithmus auf die Notwendigkeit eines neuronalen Taktes. Sie steht, was das Bindungsproblem betrifft, völlig im Einklang mit der „Korrelationstheorie“. Darüber hinaus erweitern unsere Gedanken die „Korrelationstheorie“ mit einem mathematischen Modell in den Bereich der Sprache und verbinden sie mit einem rhythmisches Konzept der sensomotorischen Handlungskontrolle.
Gehirn und Musik
Wir haben es geschafft, die komprimierende Tätigkeit der Sprache mit mathematischen und neurophysiologischen Überlegungen in einen skizzierten Zusammenhang zu stellen. Die menschlichen Sprachfähigkeiten sind jedoch nicht vollständig erfasst, solange der musikalische Bereich darin fehlt.
Musik ist auch eine Sprache, aber sie teilt nicht klar umgrenzte Vorstellungen mit wie die Wörter, sondern eher klar umrissene Gefühle. Trauer kann nicht überwältigender dargestellt werden, als im zweiten Satz von Beethovens Eroica oder in Bruckners 7. Sinfonie. Religiöse Gefühle sind bei J.S. Bachs Orgelmusik so wenig zu überhören wie in einem Gospelsong, und in Mozarts Opern werden durchgängig die wandelbaren Gefühle der Darsteller in Töne umgesetzt, so dass deren Innenleben in allen Nuancen verständlich hörbar wird.
Fragen wir also weiter: Mit welchen mathematischen und neurophysiologischen Mitteln können die Menschen den Bereich der Töne zur Darstellung und Modulation ihrer Gefühlswelt nutzbar machen.?
Die Grundlagen
Die Grundlagen der musikalischen Sprache sind Rhythmus und Harmonie, die beide bekanntlich in einer mathematischen Darstellung erfasst werden können: Die Mathematik der Harmonie ergibt sich aus den ganzzahligen Schwingungsverhältnissen der Intervalle, im Rhythmus können wir die messbare und abzählbare zeitliche Gestaltung von Metrum, Betonungen usw. zur mathematischen Betrachtung heranziehen.
Es macht Staunen, dass die Sprache der Gefühle so fest mit mathematisch beschreibbaren Prinzipien verbunden ist, und das Staunen wird noch verstärkt durch die Tatsache, dass die musikalische Sprache keine nationalen Grenzen wie andere Sprachen hat; Musik wird international von allen Menschen verstanden (wie auch die Mathematik!).
Um diesem Staunen nachzugehen, schlage ich einen gedanklichen Weg ein, der die Musik vorwiegend als eine Sprache des Körpers auffasst. Gefühle spüren wir ja über den Körper, wenn wir verliebt sind (Herzklopfen), Wut haben (Bauchschmerzen), meditieren (Wohlgefühl), Hunger und Durst leiden usw. Dementsprechend kann Musik nicht nur die Gefühle, sondern den ganzen Körper beeinflussen, mit Macht in die Beine gehen, eine Gänsehaut verursachen, einschläfern, Tränen erzeugen usw., und die dazugehörigen Gefühle stellen sich ein.
Für ein mathematisches Verständnis liegt ein Vorteil der körperlichen Betrachtung darin, dass von unserem Körper bestimmte Eigenschaften, die der Musik zu Grunde liegen, in Zahlenverhältnissen erfasst werden können. Gefühle lassen sich nicht direkt messen, sie werden nur über dem Umweg der körperlichen Symptome in Zahlen erfassbar.
Rhythmus
Eine messbare Grundlage jeder Musik, ihr Rhythmus, geht aus der rhythmischen Natur der Lebensvorgänge hervor.
Musik ist eine rhythmische Tätigkeit im bewußten Dasein der Menschen. In den vorangegangenen Abschnitten wurde beschrieben, wie nicht nur die Bewegungen, sondern auch die dahinter wirksamen Gehirnaktivitäten der bewußten Wahrnehmung und Handlungskontrolle auf einer rhythmischen Grundlage basieren.
Man kann demnach erwarten, dass ein „Pulsschlag des Geistes“ sich in der rhythmischen Dimension der Musik besonders deutlich zu erkennen gibt.
Betrachten wir den Tempobereich, in dem sich gewöhnlich der musikalische Rhythmus bewegt: Grob liegt das Spektrum musikalischer Tempi zwischen 60 und 140 bpm (Taktschläge pro Minute). Diese Taktschläge beziehen sich im Normalfall auf Viertelnoten, die noch in Achtel und Sechzehntel unterteilt werden können. Dieser Bezug auf Viertelnoten wird auch die Zählzeit genannt, weil es ein gut mitzählbares Tempo ist, während die schnelleren Notenwerte zum Zählen nicht mehr geeignet sind.
Tempo 140 ist das schnellste Tempo, das noch kontrolliert (von Virtuosen) in Sechzehntelnoten gespielt werden kann. In einer Sekunde werden dann 140x4/60=9,3 Töne gespielt.
Unkontrolliert können noch mehr Töne gespielt werden, wenn z. B. ein Pianist mit der Faust in einer Sekunde über die ganze Tastatur gleitet.
Interessant ist in diesem Zusammenhang die moderne elektronische Musik. Obwohl die körperlichen Beschränkungen bei dieser Musik wegfallen, weil die Musikcomputer mühelos noch schnellere Tempi erzeugen können, zeigt die Praxis der Diskotheken auch bei dieser Musik eine Grenze bei ca. 140 bpm. Es scheint so, dass bei diesem exstatischen Tempo von den Tänzern keine Steigerung mehr erwünscht ist, eine ästhetische Grenze.
Wichtiger als das schnellste Tempo sind die beliebigen Variationen des Tempos, in denen die Musiker stufenlos jeden von einem Metronom, Dirigenten oder Mitspieler vorgegebenen Wert aufnehmen können. Wie schnell der innere Arbeitstakt einen Rhythmus aufnehmen kann, weiß jeder Musiker. In der Regel genügen drei bis vier vorgegebene Taktschläge, damit alle Mitspieler exakt synchron das betreffende Tempo beginnen und zeitgleich durchhalten können.
Aber nicht nur die Ausführenden, auch die Zuhörer geraten augenblicklich unter den Einfluß, welchen ein spezieller Rhythmus auf unser Gehirn ausübt, und diese Resonanz des internen Taktgebers moduliert die Gefühle der Anwesenden in einer ganz spezifischen Weise. Dazu wippen viele mit den Füßen oder nehmen den Rhythmus in anderen Bewegungen ihres Körpers auf. Es gibt keine traurige Musik in flottem Tempo und keine jauchzende Freude in sehr langsamer Musik, aber das Gegenteil hört man oft, weil die musikalische Manipulation der Rhythmen eine genau bestimmbare, physiologische Wirkung auf die Gefühle hat.
Mit steigender Beatfrequenz wird die innere Anspannung bis zur Grenze von 140 bpm immer größer, sehr langsame Rhythmen wirken entspannend, können einschläfern. So verstehen wir, dass der Schlußsatz in allen Sinfonien immer der Schnellste ist, und ähnliche Gesetze auch in der Diskothek gelten. Die Aufgabe des DJ, des Mannes, der in der Disco die Platten auflegt und für die Stimmung sorgt, besteht darin, im Laufe des Abends durch gezielte Auswahl der Titel eine kontinuierliche Steigerung des Tempos von ca. 80-140 bpm auf der Tanzfläche zu steuern. Man könnte sagen, er führt sein Publikum an der rhythmischen Leine.
Wie exakt sich die Menschen aller Erdteile in ihrem musikalisch-rhythmischen Verhalten ähnlich sind, ist in allen Musikkulturen, besonders natürlich bei den Trommlern, feststellbar.
So genaue interkulturelle Übereinstimmung läßt sich als biologisch bedingte Ähnlichkeit verstehen, der „Pulsschlag des Geistes“ ist in allen menschlichen Gehirnen ähnlich wirksam.
Es wurde im vorigen Kapitel bereits erörtert, wie dieser cerebrale Pulsschlag die sensomotorischen Handlungen durch den ständigen Wechsel von Handlung und Kontrolle optimieren kann, weshalb der Handlungsrhythmus auf die halbe Taktfrequenz begrenzt ist. Bei Musikern können wir davon ausgehen, dass ihre Handlungskontrolle durch tägliche Übungen optimal trainiert ist. Wenn wir von der 140 bpm-Grenze ausgehen, kommen wir bei 9,3 Tönen pro Sekunde auf eine Taktfrequenz von 18,6 Hz. Es kommt nicht genau auf die Zahl hinter dem Komma an, aber genau diesen Frequenzbereich kennen wir bereits als eine wichtige Grenze in der Musik; sie trennt den Bereich des Rhythmus vom Bereich der Töne.
Schallwellen, deren Frequenz langsamer ist(<18), hören wir als einzelne (diskrete) Ereignisse, während wir oberhalb 18Hz nur noch kontinuierliche Töne hören. Weil diese Verschmelzungsgrenze bei ca. 18Hz auch im optischen Kanal (Kino) feststellbar ist, können wir in den Hirnwellen gleicher Frequenz den umfassenden Taktgeber vermuten, der im Gehirn die Grenze der zeitlichen Auflösung festlegt. Dann läßt sich das Verschmelzungsphänomen so deuten, dass der Eindruck von ununterbrochener Dauer entsteht, wenn jede Periode des Arbeitstaktes über einen längeren Zeitraum hinweg die gleiche oder wenig veränderte Information erhält.
Harmonie
Man könnte nach dem Sinn dieser Grenze fragen, wofür dient diese Umwandlung diskreter Wellen in kontinuierliche Töne? Eine sinnvolle Antwort ist die: Wenn wir diskrete Ereignisse >18Hz nicht mehr wahrnehmen können, weil unser cerebraler Taktgeber dafür zu langsam ist, dann ist uns mit der Unterscheidung von Tonhöhen immer noch sehr gut zur Orientierung gedient. Das Gehör ist zur Orientierung wichtiger als die Augen, weil es auch in der Dunkelheit oder im Wald aus allen Himmelsrichtungen noch Signale aufnehmen kann, wo die Augen versagen. Unsere Umwelt ist oft erfüllt mit unterschiedlichsten Frequenzgemischen, die viel zu schnell und zu kompliziert schwingen, um von uns als diskrete Wellenform erkannt zu werden. Unser Gehör kann aber aus dem Kontinuum der Töne nicht nur die Grundschwingungen, sondern gleichzeitig auch die Obertöne sehr fein differenziert erkennen, wenn es zum Beispiel eine Flöte von einer Klarinette unterscheidet. Mit ihrer Tonhöhe können wir die Unterschiede der Frequenzen sehr genau wahrnehmen und damit die feinsten Verstimmungen zwischen zwei Saiten oder Instrumenten korrigieren. Darüber hinaus können wir, wie Pythagoras von Samos vor Jahrtausenden bewies, mit dem Gehör sehr genau harmonische bzw. ganzzahlige Verhältnisse zwischen verschiedenen Tönen identifizieren und damit die Intervalle bestimmen. Der Philosoph fand heraus, dass die musikalischen Intervalle (Sekunde, Terz, Quarte, Quinte, Sexte, Septime und Oktave ) auf ganzzahligen, „harmonischen“ Verhältnissen der Saitenlängen beruhen, das Gehör also mathematische Verhältnisse der Tonhöhen sehr genau analysieren und bestimmen kann. Die Grundlagen der abendländischen Harmonielehre wurden aus dieser Erkenntnis entwickelt.
Diese gut bekannte Tatsache dient als Grundlage für alle Musik, die nicht nur Rhythmus, sondern auch Harmonie und Melodie in ihren Ablauf einschließt. Die musikalischen Intervalle sind die Basis von Harmonie und Melodie, und mit der Oktave und der Quinte ist dieses Fundament ebenso international wie die rhythmischen Grundlagen. Oktave und Quinte sind in allen Musikkulturen als herausragende Intervalle vertreten, deren exakte Bestimmung nur der analysierenden Qualität des menschlichen Gehörs zu verdanken ist.
Diese Fähigkeit, harmonische Frequenzverhältnisse mit großer Genauigkeit wahrzunehmen, ist Voraussetzung für Musik, aber sie bedarf immer noch einer Erklärung.
Die Frage lautet: Wie ist es uns möglich, in zwei Tönen mit sehr verschiedener Höhe eine Art von Verwandtschaft zu hören, der wir den Begriff „Harmonie“ zuordnen, wohinter sich ein ganzzahliges Verhältnis der Schwingungen verbirgt?
Wenn wir zwei Töne im Abstand einer Oktave hören, dann ist das Gefühl der Verwandtschaft beider Töne derartig stark, dass wir beiden Tönen sogar den gleichen Namen geben, zum Beispiel den tiefen Ton C nennen und den höheren c, dann folgend c´, usw. Die Oktavverwandtschaft ist bekanntlich Grundlage der Tonleiter, aber woraus erhält das Gehör diese Information von Verwandtschaft?
Bei der Beantwortung dieser Frage hilft uns auch nicht die Erkenntnis von Pythagoras, dass die Saitenlängen der Oktaven immer im Verhältnis 2:1 stehen, denn die Musiker oder Zuhörer wissen oft nichts von den Saitenlängen, wenn sie Oktaven wahrnehmen. Wenn ein Mann und ein Kind die gleiche Melodie singen, dann singen sie immer im Oktavabstand, auch ohne Bestimmung von Saitenlängen oder Frequenzverhältnissen, die diesen Saitenlängen entsprechen.
Es ist zunächst ein Rätsel, worauf das Gefühl von Verwandtschaft oder Ähnlichkeit basiert, das sich beim Hören einer Oktave einstellt. Die Frage erscheint noch schwieriger, wenn man bedenkt, dass die eng benachbarten Intervalle der Oktave, die große Septime und die kleine None, als starke Dissonanzen gelten und keinerlei Verwandtschaftsgefühl zum Grundton aufkommen lassen, sondern eine Spannung, die sich erst in der Oktave völlig auflöst.
Ähnliches gilt auch für die Quinte, die ein geschultes Gehör sehr genau aus allen Tonverhältnissen herausfinden kann und die immer ein Schwingungsverhältnis von 3:2 als Grundlage hat. Die Saiten der Streichinstrumente werden in Quinten gestimmt. So ist auch die Quinte weltweit in allen musikalischen Formen als vorherrschendes Intervall zu finden. Auch bei der Quinte finden wir eng benachbarte Töne (Tritonus = verminderte Quinte), die sehr unverwandt zum Grundton klingen und eine Spannung erzeugen, die sich in der Quinte auflöst.
Dialektik: Spannung und Entspannung
Eine musikalische Grundregel lautet: Immer nur Entspannung ist langweilig, ständige Spannung ist unerträglich. Deshalb ist die meiste Musik auf einen häufigen Wechsel von Entspannung und Spannung ausgerichtet, wozu die konsonanten und dissonanten Intervalle gute Dienste leisten. Viele Musikstücke bestehen harmonisch hauptsächlich auf dem ewigen Wechsel von Tonika und Dominante, womit die Musik im Wechsel von Entspannung und Spannung voranschreitet. Der Dreiklang „Dominante“ baut auf der Quinte auf und enthält die große Septime und die None zur Tonika, also zwei Intervalle mit sehr dissonanter Spannung zum Grundton. Seinen Namen erhielt der Dreiklang auf der 5.Stufe sicher durch das dominante Streben zur Grundtonart, das wir in dieser harmonischen Stufe erleben.
Die Gefühle zwischen Entspannung und Spannung sind demnach sowohl mit rhythmischen als auch mit harmonischen Mitteln zu erzeugen und über die Wahl des Tempos und der Intervalle musikalisch zu beeinflussen.
Hörgewohnheiten
Die Entwicklung der abendländischen Musiktheorie hat den harmonischen Bereich im Lauf der Jahrhunderte noch weiter differenziert, zum Beispiel in den Kategorien von Dur und Moll, in der Kadenzlehre und dem Kontrapunkt. Es ist hier nicht möglich, diese Entwicklung nachzuzeichnen, aber rückblickend kann gesagt werden, dass die harmonische Entwicklung der Musik auch eine Entwicklung der Hörgewohnheiten bewirkt hat.
Zum Beispiel war eine kleine Septime vor 300 Jahren noch eine heftige Dissonanz, die nur in der Dominante verwendet werden durfte und unbedingt in die Terz der Tonika aufgelöst werden mußte. Die vom Jazz beeinflußten Hörgewohnheiten empfinden diese Notwendigkeit und den dissonanten Charakter der Septime heute nicht mehr.
Unberührt vom Wandel der Hörgewohnheiten sind die Oktave und die Quinte immer noch die grundlegenden konsonanten Intervalle geblieben.. Eine Erklärung für dieses Phänomen haben wir bisher noch nicht.
Unbeantwortet ist die Frage, worauf das starke Gefühl einer Tonverwandtschaft beruht, wenn zu einem beliebigen Ton noch dessen Oktave oder Quinte gespielt wird. Warum erkennen wir präzise mit dem Gehör ein mathematisches Verhältnis in den Tönen und nehmen das 2:1-Verhältnis als Basis und Länge der Tonleiter?
Naturtöne
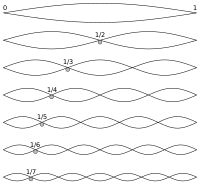
Vielleicht finden wir diese Erklärung eher in physikalischen und psychologischen Erkenntnissen. Der Physik (Akustik) verdanken wir die Erkenntnis, dass die natürlichen Töne nie aus reinen Tönen (Sinusschwingungen) bestehen, sondern immer die sogenannten Obertöne enthalten, die jedem Klang seine spezielle Klangfarbe geben. Die genau festgelegte Reihenfolge von harmonischen Intervallen, die mit jedem Ton zusammen schwingen, ist als Naturtonreihe bekannt. Jeder Klangerzeuger, zum Beispiel jedes Musikinstrument, bekommt durch seine Obertöne einen individuellen Klangcharakter, der nur mit Meßinstrumenten oder feinen Ohren erkannt werden kann. In der Obertonreihe sind alle Intervalle der Tonleiter enthalten, aber sie werden in sehr unterschiedlicher Ausprägung von den Instrumenten erzeugt. Die stärksten Obertöne sind bei den meisten Instrumenten die Oktaven und die Quinten.
Es ist sogar praktisch unmöglich, einen völlig reinen Sinuston zu erzeugen. Jeder Lautsprecher hat eine Resonanzfrequenz und einen Klirrfaktor, erzeugt also zu jeder Schwingung noch Obertöne. Mit Orgelpfeifen kommt man dem reinen Sinuston nahe, aber man vermeidet im Orgelbau diese Reinheit der Töne absichtlich und gibt den Registern der Orgel lieber Eigenschaften, die den Klang von Blasinstrumenten imitieren, z. B. Schalmei oder Trompete. Der Grund dafür liegt darin, dass die obertonarmen Töne, die reinen Sinusschwingungen, für uns leer und langweilig klingen.
Um diese uninteressante Wirkung der reinen Sinustöne zu verstehen, können wir einen Vergleich mit dem Wasser heranziehen: Es gibt in der Natur kein reines (destilliertes) Wasser. Aus jeder Quelle und Wasserleitung kommt das Wasser mit einer kleinen Menge von Salzen und Mineralien, die den Geschmack des Wassers beeinflussen. Deshalb schmeckt das Wasser aus verschiedenen Quellen unterschiedlich. Destilliertes Wasser können wir zwar herstellen, aber zum Trinken ist es völlig ungeeignet, weil ihm mit den Salzen jeder Geschmack fehlt, es schmeckt äußerst fade.
Genau so ist es mit den reinen Sinustönen, denen etwas fehlt, an dessen gesetzmäßige Coexistenz wir von Geburt an gewohnt sind. Gewohnt sind unsere Ohren besonders an die kräftigen Obertöne, die Oktave und die Quinte, und allein aus dieser Hörgewohnheit kann sich die starke subjektive Verwandtschaftsbeziehung ableiten lassen. Oktave und Quinte gehören als die kräftigsten Obertöne nun einmal zu jedem Ton, und so ergibt sich genau dann ein stimmiges Gefühl, wenn diese Töne auch noch durch andere Instrumente verstärkt werden, das paßt gut zusammen.
Umgekehrt sind die dissonanten Intervalle Tritonus, große Septime und kleine None in der Obertonreihe nicht ausgeprägt. Erklingen sie trotzdem, dann vermitteln unsere erschreckten Ohren das dissonante Gefühl, dass etwas nicht dazu gehört, nicht stimmt.
Es ist wie beim Wasser: Salz im Wasser sind wir gewöhnt, es ist auch in unserem Blut, Speichel, Urin und Schweiß vorhanden und wird von uns gern zum Würzen von Speisen genommen. Schmeckt das Wasser aber bitter, dann erregt es Abscheu und wird höchstens als Medizin getrunken. Gifte sind oft bitter, so dass die Abscheu vor Bitterem eine lebensrettende Reaktion sein kann.
Wie empfindlich unser Gehör auf unpassende Geräusche reagiert, kennt jeder Autofahrer. Das Motorgeräusch ist nicht zu überhören, aber es hat eine beruhigende Wirkung, solange keine ungewohnten Töne darin auftauchen. Fremde Geräusche wirken sofort als Alarmsignal.
So ähnlich können wir uns auch die konsonante und dissonante Wirkung der Intervalle psychologisch erklären.
Gemeinsamkeiten von Musik und Sprache
Wir haben damit für die rhythmischen und harmonischen Elemente der Musik eine Verbindung zu körperlichen und psychologischen Vorgängen sowie mathematischen Verhältnissen grob beschrieben. Man kann in diesem Zusammenhang noch der Frage nachgehen, wie weit die Sprache der Wörter mit der Sprache der Töne auf Gemeinsamkeiten zurückgreift.
Rhythmus ist nur in der Poesie so prägnant wie in der Musik, aber auch beim normalen Sprechen kann das Sprechtempo den Gefühlszustand des Sprechers ausgedrücken, mit aufgeregtem, hastigen Gerede, Gestammel, betont langsamem Reden usw. Beim Singen treten die gemeinsamen rhythmischen Wurzeln von Musik und Sprache im Pulsschlag des Geistes klar hervor.
Unser feines Gehör für Obertöne bestimmt die harmonischen Gesetze, aber es hat auch bei der Sprache eine wichtige Aufgabe: Wir können durch die Obertöne die Stimmen von Männern, Frauen, Kindern, Freunden und Fremden sehr genau identifizieren, sogar am Telefon. Noch wichtiger sind die Obertöne für das Sinnverständnis von gesprochener Sprache, denn die Vokale und Konsonanten können von uns nur im hohen Frequenzbereich gut unterschieden werden. Der Grundton kann sogar fehlen, wie es technisch bei jedem Telefon der Fall ist. Die Sprache moduliert besonders die Frequenzen über 1000Hz, und die werden vom Telefon gut übertragen. Menschen, die durch einen Hörsturz der Tonbereich über 1000Hz nicht hören können, nehmen von der Sprache nur die Grundtöne als dumpfes Geräusch ohne erkennbaren Sinn auf. Auch die Altersschwerhörigkeit betrifft die hohen Frequenzen und beeinträchtigt deshalb das Sprachverständnis.
Die Leistungen, die unser Gehör im sprachlichen und musikalischen Handeln störungsfrei in jedem Augenblick beherrschen muß, sind nicht ohne Gedächtnis zu bewältigen. Hörgewohnheiten, wie sie in der Wirkung der Intervalle bemerkbar werden, sind tiefe Gedächtnisspuren aus dem ganzen Leben. Dass sprachliche Kommunikation auch an Lernprozesse in unserem bewußten Gedächtnisspeicher gebunden ist, mag trivial erscheinen, aber die besondere Art dieser Speicherung ist immer noch ungeklärt, und deshalb kann eine weitere Gemeinsamkeit von Sprache und Musik hier noch bedacht werden.
Artikulation
Artikulation (Gliederung) ist seit Wilhelm v.Humboldts sprachtheoretischen Erkenntnissen die eigentliche Aufgabe des tätigen (sprechenden oder denkenden) Geistes.
Zitat: „...die Artikulation ist das eigentliche Wesen der Sprache, der Hebel, durch welchen sie und der Gedanke zu Stande kommt, der Schlußstein ihrer beiderseitigen, innigen Verbindung. Dasjenige aber, wessen das Denken, um den Begriff zu bilden, in der Sprache streng genommen bedarf, ist nicht eigentlich das dem Ohr wirklich Vernehmbare, oder um es anders auszudrücken, wenn man den artikulierten Laut in die Articulation und das Geräusch zerlegt, nicht dieses, sondern jene. Die Articulation beruht auf der Gewalt des Geistes über die Sprechwerkzeuge, sie zur Behandlung des Tons zu nötigen, welche der Form seines (des Geistes) Wirken entspricht...“ (III:192)
Buchstaben oder Silben werden artikuliert zu Wörtern, diese zu Sätzen, jene zu Abschnitten und Kapiteln, ganzen Bänden und Bibliotheken. Das Durchgängige ist dabei die Gliederung, die genau festlegende Reihenfolge der einzelnen Elemente, die nach Humboldt das Wesen der Sprache ausmacht.
Auch in der Musik stoßen wir auf genau vorgeschriebene Gliederungen, wenn wir die melodischen Abläufe ins Auge fassen. So wie in der Sprache die kleinsten Bauteile in beliebigen Verknüpfungen gegliedert werden können, ist es auch in der Musik mit den Tönen möglich. In der Sprache entstehen so ganze Sätze, und auch in der Musik benennt man größere melodische Zusammenhänge als Sätze.
Gliederung von Reihenfolgen ist in der Sprache wie in der Musik eine stetige Arbeit des rhythmisch tätigen Geistes. Wir können sprachlich und musikalisch beliebige Reihenfolgen erzeugen und uns diese Reihenfolgen genau merken.
Professionelle Schachspieler können sich tausende an Schachpartien Zug für Zug erinnern, Dirigenten haben ihr ganzes Repertoire verinnerlicht, Schauspieler ihre Rollen, Pianisten und viele Arten von Künstlern haben ein abendfüllendes Program genau vorgeschriebener Reihenfolgen in ihrem Gedächtnis.
Für eine theoretische Vorstellung von unserem Gedächtnis folgt daraus, dass es nicht nur als Speicher von Fakten, also von feststehenden Begriffen und Objekten, zu betrachten ist, sondern vorwiegend als Speicher für Reihenfolgen beliebiger Art.
Beispiel: Von einem Tag oder von einer Reise sind uns nicht nur die einzelnen Ansichten, Personen oder Ereignisse in Erinnerung, sondern besonders auch deren genaue zeitliche Reihenfolge.
Mit dieser alltäglich benutzten Fähigkeit zur Bildung und Speicherung von gegliederten Reihenfolgen kann der Mensch in der Sprache wie in der Musik zeitlich gestaltend tätig sein, das heißt, er kann beliebige Gliederungen erfinden und diese ganzheitlich zu einer Gestalt verbinden.
Invarianz
Was genau unter dem Begriff Gestalt zu verstehen ist, läßt sich an einer Melodie erklären. Man kann eine Melodie in beliebig hoher oder tiefer Stimmlage singen und ihr Tempo willkürlich langsam oder schnell wählen, aber in jeder Variation wird diese Melodie als ganzheitliches Gebilde erkennbar bleiben. Die einzelnen Variationen der Melodie sind durch ihre Ähnlichkeit verbunden, das grundlegende Muster aller Varianten wird ihre Gestalt genannt.
Auch Mathematiker haben schon seit ewigen Zeiten großes Interesse an Gestalten (z. B. Dreieck, Kreis usw.). Sie benutzen für den Begriff Gestalt lieber den Begriff Invariante, meinen damit aber das Gleiche: invariant ist eine Struktur, die bei Tranformationen erhalten bleibt, zum Beispiel ein Kreis, der groß oder klein sein kann, mit roter oder blauer Farbe gezeichnet, er bleibt als Gestalt oder Invariante immer Kreis.
Invarianten bzw. Gestalten sind den Ideen Platons vergleichbar, aber ihre Herkunft ist nach heutiger Sicht nicht der Himmel, sondern die Gehirne von Säugetieren, besonders Menschen.
Genau wie Melodien oder geometrische Figuren lassen sich auch die Zahlen, Buchstaben, Wörter und sonstige Symbole unter dem Begriff Gestalt oder Invariante als Ergebnisse der artikuliernden Tätigkeit des Geistes begreifen.
In mathematisch knapper Sprache dürfen wir also sagen, dass der Sprache und der Musik die Bildung von artikulierten Invarianten gemeinsam ist.
Schrift
Gemeinsam ist beiden menschlichen Ausdrucksmitteln auch eine Schriftform, die als eine Herstellungsvorschrift verstanden werden kann. So wie die Noten als Vorschrift zur Erzeugung musikalischer Gestalten dienen, sind die Buchstabenfolgen für uns Bauanleitungen für Wörter und Sätze.
Es wurde schon darauf hingewiesen, dass Herstellungsvorschriften mit genau festgelegten Reihenfolgen in der Mathematik unter dem Begriff Algorithmus zusammengefaßt werden. Ein Algorithmus, der die Vorschrift enthält, Zeichensequenzen zu produzieren, kann als komprimierte Darstellung dieser Sequenzen aufgefasst werden.
Zusammenfassung
Will man die Gemeinsamkeiten von Sprache und Musik mit wenigen Worten, mathematisch, zusammenfassen, kann man demnach sagen:
Beide Formen der menschlichen Kommunikation artikulieren im rhythmischen Spektrum der Gehirnwellen und im Bereich der Töne invariante Reihenfolgen zur Gestaltung von Vorstellungen und Gefühlen. Beide können auch in einer Schriftform komprimiert werden.
Optimale Komprimierung
Der ganze Reichtum, den wir an der Sprache und der Musik lieben, ist in der knappen mathematischen Darstellung verschwunden. Wie ein Skelett, von dem alles lebendige Fleisch entfernt ist, bringt die Mathematik nur ein Gerippe zum Ausdruck.
Aber gerade in dieser Fähigkeit, die man auch als optimale Komprimierung verstehen kann, liegt offensichtlich die Stärke der mathematischen Sprache, für die man ihren Mangel an Gefühlen gern in Kauf nimmt. „So kurz wie möglich“ ist die augenscheinliche Devise, mit der Punkte oder simple Strichzeichen an Stelle von komplizierten Handlungen übersichtlich zu Papier gebracht werden.
Die Sprache der Mathematik besteht aus speziellen Symbolen: den Zahlen, Buchstaben und Anweisungen zu ihrer Verknüpfung. Mathematiker bevorzugen die Schriftform, in der die Symbole international gleich verstanden werden; 3+4=7 gilt in allen Erdteilen als richtige Behauptung.
Die gleiche Aussage wird mit Wörtern an Stelle der fünf mathematischen Symbole auf achtundzwanzig Zeichen vergrößert, und nur noch deutschsprachigen Menschen verständlich sein: „Drei und vier ist zusammen sieben“.
Wenn wir die Wörter bereits als komprimierte Darstellungen von Vorstellungen oder Objekten begreifen, dann sind die mathematischen Symbole ähnlich wie die Abkürzungen (z.B.:DNA) zusätzliche, maximale Komprimierungen von bereits Komprimiertem.
Das beste Beispiel ist der Punkt, der die Handlungen der Multiplikation symbolisiert. Kleiner geht es nicht, und man brauchte sehr viele Wörter, um den Vorgang des Malnehmens damit zu beschreiben. Ebenso winzig sind auch der Doppelpunkt und alle Strichzeichen und Buchstaben, die für die mathematischen Tätigkeiten der Addition, Subtraktion, Division usw. als Minimalzeichen erfunden wurden.
Komprimierung ist auch bei der Benutzung von Maßeinheiten der Fall, zum Beispiel beim Messen von Entfernungen. Je nach dem Messbereich, in dem man Zählungen und Berechnungen durchführt, wählt man als Einheit Millimeter, Meter oder Kilometer, um zu überschaubaren Zahlen zu kommen. Auf der Erde reichen diese Maßstäbe, aber im Universum sind die Entfernungen so groß, daß auch die Kilometer-Einheit zu unübersichtlichen Zahlenkolonnen führt. Um wieder zu übersichtlichen Zahlen zu kommen, erfanden Kosmologen das Lichtjahr als Einheit der Länge in galaktisch komprimierten Dimensionen.
Dieser Hang zum Übersichtlichen hält uns wieder eine natürliche Grenze vor Augen, nämlich die Grenze zur Unübersichtlichkeit. Telefonnummern oder Postleitzahlen können wir noch überschauen und im Gedächtnis behalten, aber Reihenfolgen mit hundert Zahlen sind nur von Gedächtniskünstlern mit einigem Aufwand zu erfassen. Dazwischen liegt die Grenze, welche in unserem Bewusstsein die übersichtlichen Zahlenfolgen von den unübersichtlichen Sequenzen trennt. Der Leser kennt inzwischen meine Vorliebe für Grenzen, die mir bei der Erkenntnis der Natur wegweisend sind.
Kanalkapazität des Bewusstseins
Vor ungefähr 50 Jahren stellte Claude Shannon seine Theorie der Kommunikation und Information auf, in der auch die Einheit der Information, das Bit, in die Wissenschaft eingeführt wurde. Bald danach begannen viele Untersuchungen von Psychologen und Informationstheoretikern der Frage nachzugehen, wie viele Bits das menschliche Bewusstsein in einer Sekunde verarbeiten kann (Kanalkapazität). Mit Messungen der Wahrnehmung und Speicherung von unterschiedlichen Reizmustern, Messungen der Lesegeschwindigkeit und Tätigkeiten wie Klavierspiel und Schreibmaschinenschreiben kamen die Untersucher zu unterschiedlichen Ergebnissen, die aber alle im Bereich zwischen 4-5 Bits pro sek. und ca. 40 Bits pro sek. lagen.
Die Grenze unserer bewussten Auffassungsfähigkeit kann wieder auf biologische Wurzeln hinweisen, und wir stellen fest, dass die Grenze der Übersichtlichkeit (Kanalkapazität) ungefähr in dem Zahlenbereich liegt, in dem auch die cerebrale Verschmelzungsfrequenz und der „Pulsschlag des Geistes“ messbar sind.
Bemerkenswert ist die kleine Menge von Informationen, die im Bewusstsein verarbeitet wird, im Unterschied zu der Informationsmenge, die in jeder Sekunde über alle Sinnesorgane von uns aufgenommen wird. Es liegen keine genauen Messungen, sondern nur Schätzungen über diese Menge vor, die ungefähr millionenfach größer ist als die Kanalkapazität des Bewusstseins. Das bedeutet, daß eine strenge Kontrolle und Auswahl darüber stattfindet, welche Information ins Bewusstsein gelangt. Wir erleben diese Kontrolle in unserer Aufmerksamkeit, wenn wir uns auf etwas konzentrieren. Damit können wir im Partylärm Gespräche führen usw.
Der Vorteil der mathematischen Symbole kann darin gesehen werden, dass mit diesen Kürzeln die physiologische Beschränkung der Kanalkapazität überwunden werden kann, indem große Komplexe zu minimalen Formen komprimiert werden. Die Mathematiker transformieren komplex-unübersichtliche Informationen in Häppchen, die unser Geist verdauen kann.
Rechnen
Bevor mit den Zahlwörtern und Symbolen der Mathematik Aussagen in Form von Berechnungen gemacht werden können, müssen zuerst die Zahlen als Teile eines Systems begriffen werden, in dem alle Elemente in einer genau vorgeschriebenen Reihenfolge existieren. Nur in dieser artikulierten Merkfolge, die kleine Kinder jahrelang eingetrichtert bekommen, indem immer eins dazugezählt wird, nur in diesem Systemverbund sind die Zahlwörter zum Zählen und zu jeder Art von Berechnung brauchbar.
Die Reihenfolge besteht zunächst nur aus der vorgeschriebenen Folge von zehn Elementen. Daraus wird rein gedanklich das Dezimalsystem konstruiert, mit dem alle Zahlengrößen als kurze Reihenfolgen komprimiert dargestellt werden können.
Algorithmische Komprimierung
Wie gut die mathematische Sprache zur Komprimierung geeignet ist, kann noch mit weiteren Beispielen belegt werden:
Die sogenannten irrationalen Zahlen sind Brüche ohne Auflösung, also genau genommen unendlich lange Zahlenreihen im Dezimalsystem. Ein bekanntes Beispiel dafür ist jene Zahl, die mit sich selbst multipliziert (quadriert) die Zahl Zwei ergibt. An Stelle der unendlichen Zahlenreihe benutzen Mathematiker für diese Zahl nur das Wurzelzeichen über der 2, kürzer geht es nicht.
Bemerkenswert ist bei dieser mathematischen Kurzform die exakte Komprimierung der unendlichen Zahlenfolge. Exakt meint hier, daß diese kleine Herstellungsvorschrift (Wurzelziehen) eine unendliche Zahlenreihe ohne Fehler erzeugt, auch die zehntausendste Stelle hinter dem Komma wird damit noch exakt errechnet. Der winzige Algorithmus: >Wurzel aus zwei< erweist sich als optimal komprimierte Form für einen unendlichen Zahlenkomplex, und es gibt unzählig viele Vorschriften dieser Art in der Mathematik.
Zum Beispiel sehr große oder sehr kleine Zahlen können durch die Darstellung in Potenzen komprimiert werden. 10²³ ist noch im überschaubaren Bereich, während 100000000000000000000000 unübersichtlich ist, die Nullen müssen einzeln gezählt werden.
Die Repräsentation der Zahlen in der Mandelbrot-Menge
Im übersichtlichen Bereich ist auch die Formel der Mandelbrot-Menge, deren unüberschaubares Ergebnis hier schon als Grenze mit unendlich vielen skaleninvarianten Gestalten (Julia-Mengen) vorgestellt und als Modell für die innere Repräsentation des Weltwissens im Gedächtnis vorgeschlagen wurde.
Der Vorschlag kann auf seine Stichhaltigkeit überprüft werden, indem gefragt wird, ob dieses Modell (MM) des Weltwissens auch eine innere Repräsentation der Zahlen enthält, die ja bei jedem Menschen wichtige Bereiche (Raum, Zeit, Geld usw.) seines Wissens strukturieren.
Zur Beantwortung der Frage kann auf eine Besonderheit der Mandelbrot-Menge hingewiesen werden, die bisher wenig Beachtung gefunden hat.
Bei genauer Betrachtung findet man in der Grenzlinie der MM unendlich viele Kopien der Grundfigur in allen Größen und Variationen. Deren mathematischer Hintergrund besteht darin, dass jede kreisförmige Knolle und jede Satelliten-Kopie sich durch eine bestimmte Periodizität des Grenzzyklus auszeichnet, gegen den die Folge für die zugehörigen c-Werte strebt.
Die daraus entstehenden Variationen beziehen sich hauptsächlich auf die Knollengröße und die Menge der Verästelungen, die jeder Knolle entspringen. Die Anzahl der Verästelungen steht in reziproker Abhängigkeit zu der Größe der Knollen, je größer, desto weniger Äste. Die größte Knolle links in der Grundfigur hat in der Symmetrieachse nur einen Ast, die beiden (symmetrischen) zweitgrößten Knollen haben zweifache Verzweigung, die drittgrößten Knollen haben dreifache Verzweigung usw.
Mathematiker glauben nur, was ihnen bewiesen wird, und deshalb soll ein Bild der MM zunächst zeigen, daß jede natürliche Zahl in mindestens einer Verästelungsform auf jeder symmetrischen Hälfte der MM zu finden ist. Zur besseren Übersicht dient eine Darstellung der halbierten MM ohne Farben.
Die Übersicht der Grundfigur zeigt nur die größten Knollen mit den kleinsten Verästelungszahlen. Durch die eingezeichneten Zahlen wird in der Grundfigur eine Ordnung sichtbar, die sich in jeder Miniknolle wiederholt.
Die roten Zahlen zeigen genau die Reihenfolge, die beim Zählen und bei der Anordnung nach der Größe festgelegt ist, die Reihenfolge der „natürlichen“ Zahlen.
Die Zahlen mit anderen Farben zeigen, dass zwischen den Knollen auch andere Reihenfolgen existieren. Die blauen Zahlenfolgen nehmen um den Wert 2 zu, die grünen um den Wert drei, und mit den violetten Zahlen sind Verästelungsreihen mit Intervallen von vier, fünf und mehr zusätzlichen Ästen angedeutet.

Mit der Vergrößerung kann in jedem Abschnitt gezeigt werden, daß die Reihe der natürlichen Zahlen ganzzahlig unbegrenzt weiter zu kleineren Knollen mit jeweils um einen Ast größeren Verzweigungen fortgeführt wird. Die potentiell unendliche Fortsetzung der Reihe wird nur durch die aktuelle Rechenkapazität beschränkt.

Wenn man diese Ordnung der Verzweigungszahlen mit Neugier und einem Quentchen Phantasie betrachtet, kann man darin das Modell einer einfachen Rechenmaschine für die Grundrechenarten sehen. Um zu dem Ergebnis einer Addition, Subtraktion, Multiplikation oder Division zu kommen, braucht man nur Regeln, von welchem Punkt aus welche Reihenfolge in welcher Richtung bei der betreffenden Aufgabe zu benutzen ist.
Die MM wäre nicht das komplizierteste Objekt der Mathematik, wenn ihre Verästelungen damit schon ausreichend beschrieben wären. Jede auf der Grundform aufsitzende (primäre) Knolle trägt ja selbst wieder unendlich viele (sekundäre) Knöllchen von unterschiedlicher Größe und Verzweigung, auf denen wiederum unendlich viele (tertiäre) Miniaturknöllchen in ähnlicher Folge sprießen, usw. Die Anordnung der Größen und Verästelungszahlen ist jedoch bei jeder verschachtelten Knolle im Prinzip identisch mit der Grundform. Dadurch ergeben sich im Grenzbereich der MM unendlich viele Kombinationen von primären, sekundären, tertiären usw. Verzweigungsmengen nach einer systematischen Anordnung, die in dem Übersichtsbild oben mit den roten und blauen Zahlenkombinationen in der linken, größten Knolle nur angedeutet werden kann.
Weil jeder Punkt der MM eine in sich zusammenhängende Julia-Menge repräsentiert, findet man im Gebiet jeder Knolle Julia-Mengen mit dem gleichen Verästelungstyp. Jede dieser Julia-Mengen präsentiert skaleninvariant, in allen Größenordnungen, das Wesen der jeweiligen Zahl in seiner Verästelungsarchitektur.
Dazu folgende Beispiele.
Juliamengen als Repräsentanten der Zahlen
-
Juliamenge mit einfacher Verzweigung
-
Juliamenge mit zweifacher Verzweigung
-
Juliamenge mit dreifacher Verzweigung
-
Juliamenge mit vierfacher Verzweigung
-
Juliamenge mit fünffacher Verzweigung
-
Juliamenge mit sechsfacher Verzweigung
-
Juliamenge mit siebenfacher Verzweigung
-
Juliamenge mit achtfacher Verzweigung
-
Juliamenge mit neunfacher Verzweigung
-
Juliamenge mit zehnfacher Verzweigung
Die Zahlen wurden von den griechischen Mathematikern in religiöser Verehrung betrachtet, und noch vor 120 Jahren meinte der berühmte Mathematiker Leopold Kronecker:“ Die ganzen Zahlen hat der liebe Gott geschaffen, alles andere ist Menschenwerk.“
Heute wird diese Meinung kaum noch vertreten und die Zahlen gehören zu den ungeklärten Grundlagen der Mathematik.
Unsere Auffassung sieht die Zahlen in der geistigen Struktur der Menschen begründet. Als Modell für diese geistige Struktur kann die MM offensichtlich auch die mathematischen Grundlagen im menschlichen Gehirn modellieren, die Reihenfolgen der natürlichen Zahlen, geraden Zahlen und mit größeren Intervallen.
Diese Reihenfolgen wie 2,4,6,8, usw. oder 3,6,9,12, usw. sind in menschlichen Köpfen ja nicht nur bei Mathematikern eingeprägt, sondern schon bei jedem zehnjährigen Schüler, der „im Kopf“ damit rechnen kann.
Ich hoffe, daß ich mit den Bildern der MM beweisen konnte, dass diese wunderbare Formel sich als anschauliches Modell für Zahlensymbole und deren Verknüpfung in Reihenfolgen bewährt.
Damit sieht es so aus, als ob sich die Mathematiker mit den Zahlenfolgen Strukturen zunutze machen, die in der Anlage des menschlichen Geistes (Modell:MM) bereits vorgezeichnet sind. Nur der sprachliche Zugang zu diesen Strukturen, ihre Verbindung mit der Umgangssprache, muss mühevoll in der Schulzeit gelernt werden.
Ähnliche Ansichten beschrieb vor genau einhundert Jahren, im Herbst 1906, der niederländische Mathematiker Luitzen Brouwer in seiner Dissertationsarbeit. Brouwer vertrat den „Intuitionismus“ in der Mathematik, er sah in der Mathematik eine menschliche Aktivität, die dadurch entsteht, daß unser Verstand alle Erfahrung mit Sinn erfüllt, indem er sie zu Folgen von Einzelteilen ordnet. Brouwer erwartete von der Aufklärung der Verstandestätigkeit, daß dafür ein kollektives Phänomen gefunden wird, das sich mit den Mitteln der Mathematik beschreiben lässt, aber selbst auch Mathematik produziert.
„Wenn unsere Bilder unabhängig von dem kulturellen Hintergrund als ’schön’ empfunden werden, kann das unter Umständen darauf zurückführen sein, daß die Bilder uns etwas sagen über unser Gehirn, über ganz bestimmte Strukturen, die, wenn sie in Zusammenhang mit den Bildern gebracht werden, so etwas wie eine Resonanz auslösen, und diese Resonanz von uns als schön, als ästhetisch empfunden wird. Oder als vertraut. Und wenn das so wäre, dann würde dies ja bedeuten, daß diese streng mathematischen Bilder, das diese mathematischen Prozesse offenbar einen geheimnisvollen Zugang haben zu dem, was in unserem Gehirn passiert.“ Sagte der Mathematiker H.O. Peitgen, der das Apfelmännchen mit seinem Buch „The Beauty of Fraktals“ populär gemacht hat, in einem Rundfunkfeature.
Grenzbildung

Wer lange in Berlin gelebt hat, erinnert sich mit Grauen an die Grenze, die 28 Jahre lang als Mauer durch die Stadt gezogen war. Das war schon ein besonderer Ort, schwer bewacht, gefährlich, voller Absurditäten, aber an keinem anderen Ort wurde so deutlich erkennbar, dass die Politik von menschenverachtendem Wahnsinn beherrscht wurde.
Für das wissenschaftliche Verständnis von Leben, für die Biologie, muß der Begriff „Grenze“ zu den Grundbedingungen jeden Lebens gerechnet werden. Nach allem, was wir über die Entstehung des Lebens wissen, kann es sich bei den ersten Lebewesen nur um einzelne Zellen, sogenannte Ur-Zellen, gehandelt haben. Diese Zellen mögen von den Zelltypen der heutigen Organismen sehr verschieden gewesen sein, aber in jedem Fall muß das Innere der Urzelle durch eine Grenze von der Außenwelt abgeschirmt gewesen sein. Nur durch eine Trennung von „Außen“ und „Innen“ hatte das Leben eine Chance, einen Ordnungszustand gegen die ungeordneten Umwelteinflüsse zu erhalten und zu erweitern. Als Oase der Ordnung in einer ungeordneten Welt muß jedes Lebewesen sich gegen äußere Einflüsse abschirmen, um zu überleben.
Gleichzeitig mußte schon die erste biologische Grenze dazu fähig sein, nützliche Stoffe herein-, und schädliche Stoffe herauszulassen. Biologische Grenzen sind deshalb immer komplizierte Gebilde mit charakteristische Gesetzmäßigkeiten. Sie sind durch Wachstum in der Größe veränderlich und sie sind die Träger des Formenreichtums der Natur.
Ebenso finden wir auch in der unbelebten Materie Grenzen zwischen Wasser, Land und Luft. Im Kosmos sehen wir kugelförmig begrenzte Objekte (Mond und Sterne) und spiralförmige Galaxien, und sogar das schwarze Loch im Zentrum unserer Milchstraße muß eine Grenze seiner gewaltigen Anziehungskraft haben, sonst wären wir schon darin verschwunden.
Für die Wissenschaftler sind Grenzen immer interessant, besteht doch die wissenschaftliche Tätigkeit zum großen Teil aus Grenzfindung, deren Benennung und Vermessung. Zum Beispiel werden für den Arzt viele Krankheiten als Überschreitung von Norm- bzw. Grenzwerten (Blutdruck, Zucker, Temperatur usw.), erkennbar, aber man kann auch ganz allgemein sagen, dass überall, wo etwas unterschieden oder entschieden wird, eine Grenze bestimmt wird. Das können auch Sprachgrenzen, Altersgrenzen oder Grenzen des guten Geschmacks sein, alles existiert für uns in Grenzen.
Das Wort „Grenze“ stammt vom polnischen Wort „Granica“ ab und ist erst seit dem Mittelalter als Ersatz für „Scheide“ im deutschen Sprachgebrauch. Die Grenzscheide vereint noch beide Begriffe, die Markscheide, das Scheidewasser und die Ehescheidung bewahren die alte Sprachform für Trennendes, Teilendes.
Ein Unterscheidungsvermögen und die Fähigkeit, Entscheidungen zu treffen, das sind elementare Voraussetzungen für jedes über die Sinnesorgane gesteuerte Leben, nicht nur beim Menschen, nicht nur bewußt, sondern schon auf den primitiven Stufen der unbewußten, animalischen Existenz. Essbares von Ungenießbarem, Artgenossen von Feinden, weiblich von männlich zu unterscheiden und seine Entscheidungen danach zu richten, die Erfassung von solchen Grenzen gehört zu den wichtigsten Aufgaben der Nervensysteme im Tierreich.
Dass auch die bewußt-geistigen Tätigkeiten nicht ohne die Erkenntnis und die Erzeugung von Grenzen auskommt, beweist uns die Sprache selbst.
„Omnia determinatio negatio est.“ (deutsch: Jede Begriffsbestimmung ist eine Abgrenzung.) (Spinoza)
Mit Definitionen (lat:finis = Ende) bestimmen wir die Begriffe genau so, wie es schon in der biblischen Schöpfungsgeschichte steht: „Und er trennte das Licht vom Dunkel und nannte das Licht Tag und das Dunkel Nacht“ (Moses 1). Wenn wir bescheiden sind, sehen wir unser ganzes Wissen als beschränkt an, aber wir erweitern unseren Horizont bei jeder Gelegenheit, denn „die Grenzen meiner Sprache bedeuten die Grenzen meiner Welt“ (L.Wittgenstein).
Der Begriff der „Gestalt“ (Math: Invariante), dessen Bedeutung für Sprache schon im Kapitel „Gehirn und Musik“ hervorgehoben wurde, „Gestalt“ ist ohne Grenze gar nicht vorstellbar. Man kann so weit gehen, zu sagen: Allein die Grenze macht eine Gestalt erst als etwas in sich Abgeschlossenes.
Mathematik und Physik sind nicht denkbar ohne Grenzen: mit jeder Zählung einer Größe und mit jeder Messung wird eine Grenze bestimmt.
Unser Nervensystem muß folglich, um alle diese Tätigkeiten auszuführen, die Informationen aus der Umwelt selbst als Grenzen in Form von Gestalten und Messungen aufnehmen, ordnen und speichern. Die Wahrnehmung und Speicherung von Grenzen kann als ein zentrales Prinzip des Erkenntnisvermögens gesehen werden und sie muß tief im Nervensystem verankert sein.
Um diese Fähigkeit des Nervensystems zu verstehen, können drei Begriffe hilfreich sein:
Konvergenz, Divergenz und laterale Hemmung.
Konvergenz und Divergenz sind Schaltungsprinzipien , die zwischen den einzelnen Ebenen der Informationsverarbeitung im ZNS zu finden sind und deren Ergebnis eine Kontrastbildung durch die sogenannte laterale Hemmung ist.
Davon wollen wir uns eine genaue Vorstellung machen:
Jeder Rezeptor der Sinnesorgane ist in einer Informationsleitung über mehrere Ebenen von Nervenzellen mit dem Thalamus verbunden, von dem aus eine Verbindung zum Großhirn besteht.
Zwischen den einzelnen neuronalen Ebenen, die zum Beispiel schon in der Netzhaut und der Hörschnecke angelegt sind, besteht keine Eins-zu-Eins-Verbindung sondern jede Zelle ist mit vielen Neuronen in der höheren Schicht (divergierend) verbunden, und empfängt andererseits von vielen Rezeptoren oder Neuronen der darunterliegenden Schicht (konvergierend) die Signale. In einem einfachen Schema kann das Schaltungsprinzip so anschaulich gemacht werden:
Die laterale Hemmung besteht darin, dass jede der den Rezeptoren nachgeschalteten Neuronen die Erregung ihrer Nachbarzellen verringert. Das Erregungsbild, das sich daraus ergibt, bildet die ursprünglichen Muster der Reizintensität differenzierter ab, weil Übergänge verstärkt dargestellt werden, Kontraste verstärkt werden, Einzelheiten hervorgehoben werden.
Das Konvergenz-Divergenz-Prinzip hat sich schon in der evolutionären Frühzeit der Lebewesen entwickelt. Man findet es bei den Säugetieren nicht nur in der Verarbeitung der primären Sinnesdaten z.B. in der Retina, in der Cochlea und den Hautsinnen, sondern auch in den Verbindungen zwischen Thalamus und Großhirn und in der Kleinhirnstruktur.
Dieses Prinzip stellt einen wichtigen Unterschied zu den Elektronnhirnen her, denn es verwandelt alle eintreffenden diffusen Umwelteindrücke sofort in abgegrenzte Gestalten, sorgt für eine automatische Strukturierung der Daten in ganzheitlich geschlossenen Gebilden. Computer können solche Veränderungen auch berechnen, wenn sie durch ein Programm dazu geführt werden, aber sie tun es nicht wie das Nervensystem bereits mit der neuronalen „hardware“, sondern nur durch genaue Anweisungen per „software“.
Zum Beispiel bietet heute jedes Programm zur Bearbeitung digitaler Photos die Möglichkeit zum „Schärfen“ der Bilder. Mit ausgeklügelten Algorithmen wird dort genau der Effekt erzielt, den die laterale Hemmung im Nervensystem mit allen einströmenden Reizen vollbringt.
Folgende Bilder machen solche Schärfung in verschiedenen Einstellungen sichtbar und bringen damit die Wirkung der Lateralen Hemmung zum Ausdruck. Die Grautöne verschwinden aus dem Bild, die Konturen werden hervorgehoben.

Unser Großhirn bekommt also von seinen Rezeptoren bereits strukturierte Informationen zugespielt, die von der „Wirklichkeit“ der Umweltsignale stark abweichen, aber nützlich für die lebensnotwendigen Reaktionen des Organismus sind. „Grautöne“ werden zu Gunsten deutlicher Konturen unterdrückt. Dieser „Verfälschung“ des Inputs durch laterale Hemmung verdanken wir die Möglichkeit, einzelne Tonhöhen aus einem Zusammenklang zu erkennen, einzelne Instrumente in einem Orchester herauszuhören, Gestalten in Bewegung zu identifizieren, Weinsorten durch einen Schluck zu bestimmen, und dergleichen mehr.
Normalerweise bemerken wir die Verstärkung der Kontraste gar nicht, die laterale Hemmung findet tief unterhalb des Bewußtseins statt. Es gibt aber optische Täuschungen, die erst durch das Prinzip der lateralen Inhibition erklärbar werden, z.B:


Hermann-Gitter (nach Ludimar Hermann 1870, auch Hering-Gitter, nach Ewald Hering):
Beim linken Gitternetz glaubt der Betrachter, im Schnittpunkt der weißen Zwischenräume graue Flecken zu sehen.
Im rechten Gitternetz erscheinen an den Schnittpunkten der Linien helle Punkte.
Die Überbetonung der Kontraste rührt aus der Verschaltung der Rezeptoren im Auge her (laterale Hemmung).
Die Erkenntniss, dass wir von der Wirklichkeit nur den „Schleier der Maya“ in einer Verbindung von Gestalt und Wort aufnehmen können, war schon vor Jahrtausenden ein fester Bestandteil der indischen Philosophie. Platons Höhlengleichnis entsprach der gleichen Einsicht, und seit I.Kant müssen auch die modernen Philosophen davon ausgehen, dass wir das wirkliche Wirken der Realität niemals mit den Sinnen erfassen können, weil die ursprünglichen Eindrücke vor ihrer zentralen Interpretation bereits automatisch durch ein „a priori“ vorhandenes Ordnungssystem in eine Welt von begrenzten „Dingen“ in den Kategorien von Raum und Zeit verwandelt werden. Die Laterale Hemmung ist ein neurophysiologisches Korrelat des KANTschen „a priori“, sie ist die Voraussetzung von „Invarianten“, mit denen wir Zeichen und Sprache zur Kommunikation bilden.
Halten wir fest, dass Grenzbildung durch laterale Hemmung bereits in den unteren Ebenen des Nervensystems mit der Divergenz und Konvergenz seiner Leitungsarchitektur erzeugbar wird, um aus geringen Intensitätsdifferenzen der Umweltsignale zur Gestaltung von Objekten (Invarianten) zu kommen.
Wir wissen bereits, dass von der großen Informationsmenge, die in jeder Sekunde von den Rezeptoren der Sinnesorgane aufgenommen werden (circa zehn hoch sieben Bit), nur ein Bruchteil (ca. 5-20Bit) von der Kanalkapazität des Bewußtseins verarbeitet werden kann. Der größte Teil der Informationen muß auf dem Weg zur Gehirnrinde ständig wie von einem Filter aussortiert werden. Ein Teil dieser Datenreduktion wird bereits von der lateralen Hemmung geleistet, indem die diffusen Übergänge zu Gunsten der Konturen unterdrückt werden.
Die durch mehrere Stufen von Konvergenz und Divergenz strukturierten Inputsignale werden zunächst zum Mittelhirn und zum Thalamus geleitet. Dort werden die Informationen weiter analysiert. Im Mittelhirn werden bereits reflexartige Reaktionen des ganzen Körpers dadurch gesteuert, wie zum Beispiel die „automatische“ Blickwendung zu auffälligen Ereignissen (Knall, Blitz usw.).
Zur Sprache kommen die Nervensignale erst in der Gehirnrinde, aber nur durch das „Tor zum Bewußtsein“, den Thalamus. In diesem „Zwischenhirn“ muß erst eine radikale Auswahl darüber getroffen werden, welche kleine Datenmenge von ca. 5-20 Bit im Moment gerade bevorzugt wird, die Schranke zur Bewußtseinszentrale zu passieren.
Man kann sich diesen Vorgang in Analogie zur Situation der höchsten Regierungsmitglieder vorstellen, die von der gesellschaftlichen Realität nur über Statistiken von Staatssekretären informiert werden und deren menschliche Kontakte von Vorzimmerdamen und Sicherheitsbeamten bestimmt werden.
So undurchsichtig wie ein „Regierungsapparat“ ist auch das Gehirn jedes einzelnen Menschen. Mit den modernen Untersuchungsmethoden bekommt man interessante Einblicke in das lebendige Gehirn, und seit den ersten mikroskopischen Beschreibungen vor >100 Jahren steht das Gehirn weltweit im Brennpunkt der Wissenschaft, aber eine verständliche Theorie seiner Hierarchie existiert noch nicht in dem Umfang, dass die Auswahlvorgänge zwischen Thalamus und Cortex, das „assoziative“ Gedächtnis und die Sprachfunktion restlos geklärt sind.
Ein verbessertes, ganzheitliches Verständnis für komplexe Dinge erhält man auch mit einer historischen Rückschau darauf, wie die Dinge sich aus einfachen Anfängen entwickelt haben. Mit diesem Vorsatz beschreibt das nächste Kapitel die Evolution der Großhirnrinde, eines Organs, dessen Aufgabe von Anfang an die Herstellung einer Einheit aus Wahrnehmungen, Gefühlen und Gedächtnis war, wie sie bereits von Aristoteles als Sensus communis beschrieben wurde.
Die Betonung der Funktion eines Sensus communis erscheint notwendig, weil die Hirnforschung bisher vorrangig an einer Aufteilung der Hirnrinde in Regionen mit unterschiedlicher Funktion gearbeitet hat. Diese Aufteilungen des Cortex in sensorische Projektionsgebiete, Assoziationsgebiete, motorische Areale, Sprachzentren usw. sind gesicherte Erkenntnisse und sollen nicht bezweifelt werden. Sie verdecken aber die Notwendigkeit, den Cortex auch als eine Ebene der Vereinheitlichung zu betrachten, in dem alle Gebiete, Areale und Zentren zu einer organischen Ganzheit verbunden sind. Es muß hervorgehoben werden, dass sowohl eine Unterteilung der Hirnrinde in Areale als auch eine Zusammenführung derselben zu einer Einheit jeweils wichtige Gesichtspunkte sind, um der Funktion des Cortex gerecht zu werden. Der folgende Abschnitt soll diese komplementäre Sichtweise ermöglichen.
Die Evolution des Großhirns
Das menschliche Gehirn ist keine Neuentwicklung der Natur. Es hat sich wie alle anderen Organe aus einfachen Formen entwickelt. Um das Gehirn von seiner einfachen Seite zu sehen, ist ein Blick auf seine Entwicklungsgeschichte nützlich. Die Entwicklung der Wirbeltiere verlief über ca. 1 Milliarde Jahre, aber jedes menschliche Embryo geht in den ersten Wochen durch alle Stadien dieser Evolution.
Das Nervensystem entwickelt sich aus einer sehr einfachen Struktur, dem äußeren Keimblatt (Ektoderm). Daß ein Organ der Informationsverarbeitung aus der äußeren Grenzschicht entsteht, ist leicht verständlich, weil hier die Reize aus der Umwelt auftreffen. Erst im Lauf der Evolution wurden die empfindlichen Nervenverbände in die Tiefe des Neuralrohrs verlegt, weil sie dort besser geschützt sind. Die Verbindungen zur Außenwelt blieben über die nun spezialisierten Sinnesorgane bestehen.
Mit der Entstehung spezialisierter Sinnesorgane ist die Bildung einer Nervenzentrale verbunden, die den ganzen Körper einheitlich nach den Sinneseindrücken steuern kann. Weil sich schon früh in der Geschichte der Wirbeltiere Augen, Ohren und chemische Sinne (Geschmack, Geruch) ausbilden, ist das Gehirn aller Wirbeltiere in gleicher Art zur zentralen Integration dieser Sinne konstruiert. Es besteht zunächst aus drei Abschnitten:
1.: Im Übergang vom Hals zum Kopf liegt das Stammhirn, welches die Atmung und die Herztätigkeit zentral steuert. Außerdem verfügt es über Rezeptoren für die Mundöffnung, die für die Nahrungsaufnahme wichtig sind (Geschmack).
2.: Das Mittelhirn verbindet die optischen und akustischen Sinnesorgane mit der Körpermuskulatur durch Reflexbögen, die automatische Bewegungen steuern.
3.: Der Rezeptor des Endhirns ist das Geruchsorgan, das sich erst bei den landlebenden Tieren entwickeln kann. Weil der Geruchsinn ein allgemeines Warn- und Reizsystem hoher Empfindlichkeit ist, aber wenig über die räumliche Situation bzw. den Ort der Reizquelle aussagt, ist für das Riechhirn eine Verbindung mit den optischen und akustischen Zentren des Mittelhirns notwendig, mit der alle Sinnesqualitäten auf einer gemeinsamen Ebene vereinigt werden.
Diese gemeinsame Ebene entsteht schon bei den Reptilien aus einer Erweiterung des Endhirns als Telencephalon oder rudimentärer Cortex. Bereits bei Fröschen und Salamandern ist diese Hirnstruktur für die Integration der verschiedenartigen Reize angelegt. Für die Umschaltung der Seh,-Tast- und Hörwelt vom Mittelhirn auf das Endhirn entwickelt sich ein Teil des Vorderhirns, das Zwischenhirn. Aus ihm entsteht der Thalamus, der aus mehreren Kerngruppen die spezifischen Signale des Mittelhirns zu spezifischen Regionen des Cortex sendet. Man bezeichnet diese Anordnung als ein Projektionssystem, die Anatomen nennen den Thalamus das „Tor zum Bewusstsein“.
Mit dem Wegfall des Schuppenkleides der Fische bzw. der Hornschuppen der Reptilien wird bei den Säugetieren die ganze Haut zu einem empfindlichen Sinnesorgan, das ebenso über Projektionsbahnen im Cortex mit den übrigen Sinnesqualitäten in ganzheitliche Verbindung kommt.
Eine Nervenzentrale, in der alle Qualitäten von Signalen zusammengeführt werden, wäre nicht sinnvoll, wenn in ihr keine Befehle für das Verhalten des Organismus gebildet und an die ausführenden Organe geleitet werden könnten. Weil das Geruchsorgan von Anfang an einen steuernden Zugriff auf komplexe Verhaltensweisen hat, kann das zum Integrationszentrum aller Sinne erweiterte Riechhirn auf diese Steuerungsbahnen zurückgreifen, um aus der Zusammenfassung aller Empfindungen ganzheitliche Verhaltensschritte zu entwickeln.
Dieses Integrationsleistung des Neocortex, die alle Sinne zu einem Ganzen verbindet und sinnvolle Verhaltensmuster daraus herstellt, ermöglicht bereits Ratten, Katzen usw. ein intelligentes Verhalten, das wir bei Insekten oder einfachen Organismen so nicht kennen. Dabei zeigt sich, dass schon Vögel und Mäuse ihr integratives Zentrum, die Hirnrinde, nicht nur als Kommandozentrale, sondern auch als besonders leistungsfähigen Informationsspeicher (Gedächtnis) nutzen können.
Beispiel: Eine Fliege lernt es nie, den Zusammenstoß mit einer Fensterscheibe zu vermeiden, während ein Vogel nach einigen Erfahrungen einen vorsichtigen Umgang mit der durchsichtigen Wand lernt.
Nur Tiere, die über einen Cortex verfügen, können dressiert werden, das heißt, sie entwickeln ein Gedächtnis für sprachliche Anweisungen, die sogar über die angeborenen Verhaltensmustern dominieren können. Deutlich ist diese Lernfähigkeit bei den Delphinen, die als Säugetiere mit mächtigem Cortex ausgestattet und gut dressierbar sind, während die relativ großhirnlosen Haie zur Dressur bekanntlich wenig geeignet sind. Indische Elefanten, die als Arbeitstiere eingesetzt werden, verstehen ungefähr einhundert menschliche Befehle.
Lebewesen, die kein Großhirn haben (z. B. Insekten), wirken wie seelenlose Automaten auf uns. Mit der Entwicklung des Cortex kommt zunehmend eine spielerische Phase bei den Jungtieren zum Vorschein, die als Lernphase der Hirnrinde zu verstehen ist und uns den Eindruck vermittelt, dass diese Tiere (z. B. Hunde, Katzen usw.) ähnliche geistige Zustände wie die Menschen empfinden.
Eine mächtige Entwicklung der Großhirnrinde wurde bei den Affen durch die Sonderstellung der Hände ausgelöst. Als bei den Säugetieren noch alle vier Extremitäten ausschließlich zur Fortbewegung dienten, genügten einfache Reflexmuster auf Rückenmarksebene dazu, den harmonischen Laufrhythmus zu steuern. Bei den Primaten geschieht ein Wandel der Fortbewegung, vom Vierfüßler zum Klettertier. Damit kommt es zu einer Umkonstruktion der vorderen Extremitäten, die zu Greifinstrumenten werden. Das alte Bewegungsmuster der Vierfüßler ist damit überfordert, aber das corticale Zentrum kann sich durch massives Wachstum der Großhirnrinde den neuen Anforderungen der Handmotorik anpassen.
Zusätzlich ist bei den Säugern das Kleinhirn in Verbindung mit dem Gleichgewichtsorgan für die Ausführung komplizierter Bewegungsabläufe in das motorische System integriert. Aufrechtes Laufen auf zwei Beinen ist ohne diese Hirnstrukturen nicht möglich.
Die Zusammenarbeit zwischen Cortex und Kleinhirn lässt sich am Beispiel des Radfahrens so erklären: Die Entscheidung über Rechtskurve oder Bremsvorgang trifft der Cortex, während die Feinarbeit der Gewichtsverlagerung und viele automatische Bewegungsimpulse im Kleinhirn bearbeitet werden.
Bei den Affen hat sich die Stellung der Augen im Gesichtsfeld so geändert, dass immer ein räumliches Bild der Umwelt gesehen wird. Für die zentrale Auswertung der binokularen Bilder müssen neue Analysatoren in das System integriert werden, und auch dabei erweist sich die Großhirnrinde als anpassungsfähiges Integrationszentrum mit riesigem Speichervermögen für komplexe visuelle Information.
Mit dieser Ausstattung war der homo erektus für den aufrechten Gang in der Savanne gut gerüstet und konnte den Geruchssinn zugunsten der Fernsinne (Augen und Ohren) vernachlässigen. Der Cortex passte sich seinen neuen Anforderungen an, indem er seine Fläche durch Faltenbildung vergrößerte.
So weit ist das biologische Standardwissen detailliert erforscht und beweist, dass die Großhirnrinde von Anfang an für die Herstellung einer ganzheitlich vereinigten Projektion und Speicherung aller Umweltsignale und einer daraus basierenden Verhaltenssteuerung spezialisiert war und diese Aufgabe in der Evolution immer stärker ausdehnen konnte. Ein besonderer Speichermechanismus ist verantwortlich für die Lernprozesse dieser Integrationszentrale, die den Lebewesen neben der starren, genetischen Anpassung eine flexible Anpassung an beliebige neue Situationen ermöglichen.
Die ersten Menschen hatten mit diesem Gedächtnisorgan und einem verbesserten Kehlkopf die Grundlage für die Verfeinerung der äffischen Laut-, und Gebärdensprache. Die veränderte Daumenstellung erleichterte den Gebrauch von Werkzeugen und sorgte für weitere Ausdehnung der Hirnrindentätigkeit. Die Evolution des Cortex ist nachvollziehbar. Es fehlt nur noch eine wissenschaftlich geprüfte Erklärung für die erstaunliche Leistungsfähigkeit, die sich in dem grauen Teppich unter der Schädeldecke als Bewusstsein, Gedächtnis und Sprache manifestiert.
Die Evolution des Frontalhirns
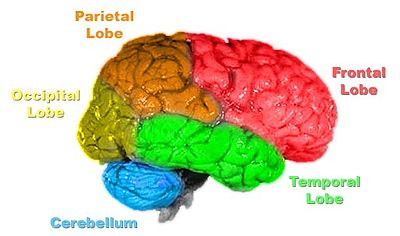
Wenn man die Großhirnrinde in sensible und motorische Bereiche eingeteilt hat, dann fällt noch der große frontale Teil auf, der weder zum sensorischen noch zum motorischen Cortex gerechnet wird, obwohl er etwa ein Viertel der ganzen Rinde ausmacht.
Die Ausbildung eines Frontalhirns geschieht erst sehr spät in der Evolution der Affen. Es hat bei den Menschenaffen schon eine Faltung, aber erst beim Menschen entwickelt das Frontalhirn sich zu einer Größe, die schon äußerlich an der (Denker)Stirn erkennbar ist.
Der mediobasale Anteil des Frontalhirns hat Verbindungen zum Hypothalamus, zum limbischen System und zum Hippocampus, also zu den emotionalen und vegetativen Zentren.
Der konvexe Teil des Frontalhirns hat zahlreiche Verbindungen zu allen motorischen und sensorischen Teilen des Großhirns, zur Formatio reticularis des Hirnstamms und besonders auch zu den Augenmuskeln, welche die Augen der Aufmerksamkeit folgen lassen.
Weil die elektrische Reizung und selbst die Entfernung des Frontalhirns bei Tieren keinen Einfluss auf die Wahrnehmung und Motorik hatten, waren die Hirnforscher sich lange nicht sicher, ob dieser Hirnteil überhaupt eine Funktion hat. Auffällig bei Schäden des Frontalhirns waren zuerst diffuse Änderungen des Verhaltens, das bei Versuchstieren und Menschen ungesteuert und planlos wirkte.
Der 2.Weltkrieg hinterließ in Russland viele Menschen mit Schussverletzungen im Gehirn. Der russische Neurologe Alexander Luria untersuchte mit ausgeklügelten Testmethoden die Folgen der umschriebenen Verletzungen, um die Ergebnisse in seinem Buch „Die höheren kortikalen Funktionen des Menschen und seine Störungen bei örtlichen Hirnverletzungen“(1970) zu beschreiben.
Fasst man die Ergebnisse dieser Studien zusammen, dann führen Schäden im Frontalhirn dazu, dass die Personen keine Aufgaben mehr bewältigen können, die in mehreren Schritten zu einem Ziel führen. Diese Menschen haben keine neurologischen Ausfälle, können sich normal bewegen und verstehen auch Sprache, aber sie können einfache Rhythmen nicht klopfend wiederholen, können keine Rechenaufgaben in mehreren Schritten bewältigen, können keine zusammenhängenden Geschichten erzählen, können keine einfachen Konstruktionen mit Klötzchen herstellen, keine zielgerichteten Aufgaben fehlerfrei ausführen.
Eine tiefgreifende Persönlichkeitsveränderung, der Zerfall von successiven Handlungen in sinnlose Automatismen und eine euphorische Kritiklosigkeit oder Gleichgültigkeit begleiten alle Schäden des Frontalhirns.
Die Untersuchungen von Luria lassen den Schluss zu, dass im Frontalhirn die Synthese der successiven Ordnung für zielgerichtete Handlungen gemeinsam mit einer Erfolgskontrolle der einzelnen Schritte stattfindet.
Wir sind bereits über die gliedernde Tätigkeit der Musik und der Sprache zu der Ansicht gekommen, dass ein wichtiger Teil der menschlichen Gedächtnisleistung in der Speicherung von invarianten Sequenzen wie z. B. Melodien, Gedichten usw. gesehen werden muss. Alle diese umfangreich artikulierenden Leistungen von Schauspielern, Musikern, Schachprofis usw. sind nach heutiger Sicht im Frontalhirn zu suchen, der frontale Cortex kann als der kreative Teil der Hirnrinde gesehen werden, auch wenn wir noch keine Ahnung davon haben, wie invariante Reihenfolgen dort erzeugt und gespeichert werden.
Hemisphärendominanz und Sprachzentren
Schon bei der Herstellung von Faustkeilen mit scharfen Klingen ergab sich eine Aufgabenteilung für die beiden Hände, indem eine Hand zum Festhalten und die zweite Hand für gestaltende Feinarbeiten bevorzugt wurden. Viele Tätigkeiten mit Werkzeugen fördern eine differenzierte Spezialisierung der Hände, und spätestens beim systematischen Training des Schreibens ist eine dominante Hand kaum noch zu vermeiden.
Dementsprechend unterscheiden sich die beiden Seiten der Hirnrinde im Lauf der Evolution und der individuellen Entwicklung zunehmend, und nur auf der Seite der schreibenden Hand wird zusammen mit den Buchstabenverbindungen auch die Artikulation der Sprache gründlich trainiert. Weil die Nervenbahn des rechten Armes im linken Cortex beginnt, liegen auch die Sprachzentren im linken Großhirn, das deshalb als die dominante Hemisphäre bezeichnet wird.
Bei Linkshändern sind die schreibenden und sprechenden Aktivitäten meist im rechten Großhirn lokalisiert, und auch nach Verletzungen oder Krankheiten der linken Sprachregionen findet ein neues Lernen der Sprache in der gesunden rechten Hälfte des Großhirns statt. Man spricht in diesem Zusammenhang von einer großen Plastizität der Hirnrinde, in der zerstörte Funktionen wieder durch neue Lernvorgänge in intakten Regionen ersetzt werden können.
Die große Oberfläche der Hirnrinde bietet neben den sensorischen Projektionszentren und dem motorischen (praezentralen) Rindenfeld noch sehr viel Platz für sogenannte Assoziationsfelder, in denen die Verbindungen zwischen optischen, akustischen, somatosensorischen und motorischen Ereignissen vielfältig verknüpft werden. Jedes sensorische Projektionsfeld kann noch in drei funktionelle Einheiten aufgeteilt werden, in ein primäres Projektionszentrum, um dessen Peripherie ein sekundäres und ein tertiäres Umfeld für spezielle Aufgaben bereit sind, zum Beispiel für das Erkennen von Gesichtern, die räumliche Orientierung und viele komplexe Wahrnehmungen und Tätigkeiten.
Zwischen diesen sinnesspezifischen Zonen befinden sich die integrierenden Verbindungen der optischen, akustischen und somatosensorischen Analysatoren in den „Assoziationsfeldern.“ Diese Felder sind stark an der Bildung von Gedächtnisspuren beteiligt, in denen mehrere Empfindungsqualitäten gemeinsam beteiligt sind.
Eine ähnliche Aufteilung existiert auch im motorischen Gebiet, in dem ein primäres Gebiet (Area4) die efferenten motorischen Signale an den Betz'schen Riesenzellen ausbildet, während um diese primäre Zone herum eine sekundäre und tertiäre Zone für spezielle Aufgaben zur Verfügung stehen. Zu diesen speziellen motorischen Aufgaben gehören zum Beispiel die Steuerung der Augenbewegungen im Zusammenhang mit Körperbewegungen und die artikulierenden Leistungen des Sprachapparates.
Das motorische Zentrum des ganzen Körpers liegt im Gyrus praezentralis bekanntlich in einer Anordnung vor, die als „Homunkulus“ kartographiert wurde, wie das rechte Bild zeigt.

Sehr deutlich ist zu erkennen, daß die Rindengebiete für die Hand und die Sprachwerkzeuge des Mundes überproportional groß gegenüber dem Rest der Körperprojektion sind. Offensichtlich entspricht die Ausdehnung dieser motorischen Rindengebiete den vielseitigen Anforderungen ihrer ausführenden Organe unter anderem beim Schreiben und Sprechen (und Essen!).
Es versteht sich leicht, daß ein Zentrum zur motorischen Artikulation der Sprechvorgänge in unmittelbarer Nähe zu dem motorischen Zentrum der Sprechwerkzeuge liegt.

Dieses Sprachzentrum liegt vor dem motorischen Gebiet der Mundregion und heißt nach seinem Entdecker (1861) Broca-Zentrum.
Bei seiner Zerstörung versteht der Betroffene die Sprache, aber er kann selbst nicht eine fließende Verbindung von Artikulationen bilden, spricht abgehackt im „Telegrammstil“. (motorische Broca-Aphasie).
Das zweite Rindengebiet, dessen Zerstörung zu einer Aphasie führt, wurde 1874 von Wernicke im linken Temporallappen in der Nähe des akustischen Projektionszentrums entdeckt. Bei Ausfällen in dieser Region ist vor allem das Sprachverständnis gestört. Die Patienten können noch alle Töne hören, aber sie können aus sprachlichen Artikulationen keinen Sinn bilden und deshalb auch nicht sinnvoll sprechen (sensorische oder Wernicke-Aphasie).
Im letzten Jahrhundert sind viele Untersuchungen zu der Ansicht gekommen, daß die Sprachfähigkeiten nicht auf diese beiden klassischen Zentren beschränkt sind. Die umfangreichsten Untersuchungen über die speziellen Störungen in speziellen Gebieten wurden ausführlich von A.R.Luria beschrieben.
Bei Schäden im praemotorischen Teil des linken Frontalhirns beobachtete er eine verbale Aspontanität, die er „kinetische Aphasie“ nannte und als Störung der kinetischen Organisation der Sprache deutete. Zusammen mit gehemmten Denkvorgängen erscheint bei diesen Patienten das Verständnis von Sinn gestört. Sie können Sätze nachsprechen, verstehen diese aber nicht und können selbst keine sinnvollen Zusammenhänge formulieren. Auch die Sprachmelodie fehlt bei diesen Schädigungen in der Regel völlig, ähnlich wie bei dem Telegrammstil der Broca-Aphasie.
Ein sensorisches Gegenstück zu dieser kinetischen Aphasie beschrieb Luria bei Schäden im mittleren Temporallappen, unterhalb des Wernicke-Zentrums. In diesem Assoziationsgebiet kommt es zu Verbindungen des akustischen Analysators mit dem occipitalen, optischen Cortex. Bei Ausfällen scheint die Synthese der optischen Vorstellungen oder das Erfassen dieser Beziehungen gestört, wodurch vor allem Kopfrechnen, Lesen und Schreiben gestört sind (Akalkulie, Alexie, Agraphie). Diese Störung wurde „akustisch-mnestische Aphasie“ genannt.
Bei entsprechenden Verletzungen in der nicht-dominanten Hirnhälfte wurde eine tiefgehende Störung der musikalischen Wahrnehmung beobachtet. Vorgegebene Tonfolgen und Klopfrhythmen können nicht erkannt und deshalb nicht wiederholt werden. Auch zu dieser „sensorischen Amusie“ gibt es ein motorisches Gegenstück im rechten frontalen Cortex, wo Verletzungen eine „motorische Amusie“ bewirken.
Eine strenge Systematik ist bei diesen Untersuchungen dadurch erschwert, daß jede verletzte Person einen einmaligen Verlauf dieser Störungen durchlebt.
So viel läßt sich aber sagen, daß die vollständige Verarbeitung von Sprache im Großhirn nicht auf die Areale von Broca und Wernicke beschränkt ist. Wenn man neben der Aphasie auch die Akalkulie, Agraphie, Alexie und Amusie zu den sprachlichen Defekten rechnet, dann sind auch die „Assoziationsgebiete“ der Hirnrinde für die ganzheitliche Entstehungsweise der Sprache heranzuziehen, und sogar die rechte bzw. nicht-dominante Hirnhälfte trägt ihren musikalischen Teil dazu bei.
Ergänzend muß noch bemerkt werden: Auch das Kleinhirn trägt mit seiner Steuerung der Feinmotorik wichtige Komponenten zum flüssigen Sprechen und Schreiben bei. Bei Schäden im Kleinhirn (Cerebelläre Ataxie) sind Sprache und Schriftbild oft „verwaschen“.
Der Hirnschrittmacher
Der Leser hat nun eine Vorstellung,
- wo Sprache im Gehirn verarbeitet wird,
- wie Grenzen für Unterscheidungen und Entscheidungen im Nervensystem hergestellt werden,
- und er hat von der Korrelationstheorie und dem „Pulsschlag des Geistes“ so viel gelesen, daß er in den rhythmischen Spannungsschwankungen der Hirnrinde eine wichtige Funktion beim Aufbau der phänomenalen Ganzheit des Bewußtseins ahnen kann.
Um diese Ahnung zu bekräftigen, sind genauere Kenntnisse über die Entstehung und die Wirkung dieser Spannungsschwankungen nötig. Die Gehirnrinde kann nicht isoliert betrachtet werden. Der synchrone Rhythmus der EEG-Wellen wird nicht in der Rinde erzeugt. Er wird der Hirnrinde aufgezwungen von einem Teil des Nervensystems, welches bisher noch nicht genannt wurde, den unspezifischen Kernen des Thalamus.
Bei allen Wirbeltieren liegen zwischen den eindeutig abgrenzbaren Bahnen und Kernen des Nervensystems Nervenzellgruppen und die dazugehörigen Fasern in einer diffusen, netzartigen Anordnung, der Netzsubstanz Formatio reticularis, die vom Rückenmark bis in den Thalamus das ganze Zentralnervensystem durchzieht.
Die Aufgabe dieser diffusen Nervennetze besteht darin, die Zusammenarbeit des ganzen Systems zeitlich zu koordinieren, z.B. den zeitlich abgestuften Einsatz von Muskelaktivitäten bei der Fortbewegung. Derartige Netzwerke zur zeitlichen Koordinierung der Nerventätigkeit sind in allen Wirbeltierhirnen, aber auch bei Insekten und niederen Tieren, nachweisbar.
ARAS
→ Hauptartikel: Aufsteigendes retikuläres Aktivierungssystem
Eine besondere Aufgabe kommt der Formatio reticularis bei den Säugetieren im Zusammenhang mit der Entwicklung der Großhirnrinde (Cortex) zu. Auch die corticalen Aktivitäten müssen mit dem ganzen System zeitlich koordiniert werden. Zu diesem Zweck gehen von der Netzsubstanz des Thalamus Verbindungen in alle Teile des Cortex, die „Aufsteigendes Reticuläres Aktivierendes System“ (abgekürzt ARAS) genannt werden.
Weil vom Thalamus auch die spezifischen Informationen der Sinnesorgane zum Cortex weitergeleitet werden, werden die ARAS – Verbindungen auch als die „unspezifischen Bahnen“ bezeichnet.

Bevor diese „unspezifischen Bahnen“ vom Thalamus ausgehend den Cortex erreichen, machen sie eine Schleife zu den sogenannten „Basalganglien“ (Nucleus caudatus, Pallidum, Putamen,Stratum), die als längliches Kerngebiet zwischen Thalamus und Cortex liegen. In dieser Erregungsschleife, die über viele Zwischenneurone in der Laufzeit fein regulierbar ist, entsteht im Thalamus ein variabler Rhythmus, der synchron in alle Gebiete des Cortex geleitet wird. Eine genaue Beschreibung dieser (rechts skizzierten) neuronalen Verbindungen findet man unter Aufsteigendes retikuläres Aktivierungssystem Mit einer rhythmischen Erregung der corticalen Pyramidenzellen durch das ARAS entsteht das, was wir „Bewußtsein“ nennen, aber nur, wenn die Frequenz schneller als 6Hz ist, und wir werden immer „wacher“, je schneller der Rhythmus wird, bis zu ca. 40Hz.
Wenn der Rhythmus langsamer als 6Hz ist, schläft der Mensch, bei 3Hz ist er in Tiefschlaf oder Narkose, und die Null-Linie im EEG wird als Todeszeichen angesehen.
Eine allgemeinverständliche Bezeichnung für ARAS wäre demnach „Hirnschrittmacher“. Wie aktuell diese Struktur und Funktion in der Hirnforschung ist, zeigen die Bestrebungen, künstliche „Hirnschrittmacher“ bei Krankheiten dieses Systems (zunächst bei der Parkinson-Krankheit) einzusetzen.
Weitere Auswirkungen des Hirnschrittmachers lassen sich in dem „Weckreiz“ erkennen, der aus tiefem Schlaf reißt. So spricht man auch von der filtrierenden Wirkung des Thalamus, die nur starke oder „wichtige“ Informationen ins Bewusstsein lässt. „Tor zum Bewusstsein“ wird der Thalamus in der Anatomie schon lange genannt, und die Frequenz des ARAS bestimmt, wie weit dieses Tor offen ist. Starke Reize bewirken augenblicklich eine Beschleunigung der Schrittmacherfrequenz, um sofort hellwach zu machen, das Tor zum Bewusstsein weit zu öffnen.
Eine weitere Auswirkung ist die Steuerung der „Aufmerksamkeit“, die so verständlich wird:
Weil im Thalamus die von den Sinnesorganen einströmenden Daten und die retikulären Strukturen des ARAS in unmittelbarer Nähe und Verbindung sind, können die Sinneserregungen dort auf die Aktivität des ARAS in der Art Einfluss nehmen, dass genau jene Teile des Cortex aktiviert werden, in welche die stärksten Sinneseindrücke projiziert werden, also die entsprechenden Gebiete der Projektionsfelder.
Weil vom Cortex auch Leitungsbahnen zum Thalamus zurückführen, kann der Cortex auch die Aktivität des ARAS „rückwirkend“ beeinflussen und die „Aufmerksamkeit“ unabhängig von äußeren Reizen in jedes corticale Gebiet lenken oder auf einen Punkt fixieren usw.
Der Wald der Erkenntnis


Das Großhirn wäre unvollständig beschrieben ohne eine Darstellung seiner Feinstruktur, die nur bei bestimmten Färbemethoden unter dem Mikroskop zu sehen ist.
Verglichen mit ihren vielfältigen Fähigkeiten ist der Aufbau der Großhirnrinde bemerkenswert eintönig. Abgesehen von wenigen feinen Unterscheidungen im Allocortex sieht die Hirnrinde (Isocortex) zu >90% überall gleich aus. Sie ist aus sechs Schichten aufgebaut, in denen jeweils spezielle Anordnungen der Nervenzellen oder ihrer Fasern zu sehen sind.
Spezifisch für die Großhirnrinde sind die Pyramidenzellen , ein Typus besonders großer Nervenzellen. Sie haben ihren Namen nach der Gestalt ihres Zellkörpers, der dreizipfelig einer Pyramide ähnelt. Besonders lang sind die Fortsätze (Axone) der Pyramidenzellen, die sich im ganzen Körper ausbreiten können und alle anderen Teile des Gehirns erreichen können, z.B. starke Verbindungen zum Kleinhirn haben. Diese Zellform kommt nur in der Großhirnrinde der Säugetiere vor, wo sie den größten Teil der Nervenzellen ausmacht.
Pyramidenzellen stehen im gesamten Cortex dicht bei dicht wie Säulen in vertikaler Ausrichtung, vorwiegend in der dritten und fünften Rindenschicht. Ihre feinen Dendriten zeichnen sich durch strickleiterförmig (John C. Eccles beschreibt sie „patronengürtelförmig“) angeordnete, erregende Kontakte mit Sternzellen aus, während am Zellkörper überwiegend hemmende Synapsen sitzen. Das Axon verzweigt sich wurzelförmig in verschiedene Richtungen und überträgt erregende Impulse auf etliche, zum Teil weit entfernte Zellen in alle corticalen Regionen.
Als morphologische Besonderheit der Pyramidenzelle muss neben dem großen Zellkörper die Fähigkeit gesehen werden, sehr lange Verbindungsleitungen zu bilden, die in der Pyramidenbahn bis zu zwei Meter lang sein können. Diese längsten Axone haben auch die größten Zellkörper unter den Pyramidenzellen, die Betz'schen Riesenzellen im motorischen Cortex.
Eingehende Informationen (Afferenzen)
Jede Pyramidenzelle erhält zwei verschiedene Formen der afferenten Erregung, spezifische und unspezifische.
- Die spezifischen Afferenzen führen die Informationen der Sinnesorgane vom Thalamus zum Cortex, sie enden am Zellkörper.
- Die unspezifischen Erregungen und Hemmungen der Pyramidenzellen stammen aus dem unspezifischen Aktivierungssystem der Formatio reticularis und gelangen in einer oszillierenden Schleife vom Thalamus über die Basalganglien in die Hirnrinde. Hier werden sie erst auf Sternzellen umgeschaltet, die wiederum mit einer speziellen, strickleiterförmigen synaptischen Verbindung auf die Dendriten der Pyramidenzellen einwirken.
Diese unspezifischen Erregungen vom reticulären Teil des Thalamus sind rhythmisch und wirken synchron über den ganzen Cortex auf den Grad der Wachheit und Aufmerksamkeit aktivierend oder hemmend ein. Wenn sie langsamer als 6 Hz sind, wird die Hirnrinde in Schlaf versetzt. Im Schlaf reagieren die Pyramidenzellen kaum noch auf Reize, nur sehr starke „Weckreize“ bringen sie zur Erregung.
Die elektrischen Spannungsschwankungen, die auf der Kopfhaut mit dem Elektroenzephalogramm| registriert werden können, sind Ausdruck dieser synchronen unspezifischen Erregungen der Pyramidenzellen.
Herausgehende Informationen (Efferenzen)
Noch schwieriger als die eingehenden Signale sind die Output-Verbindungen des Cortex zu beschreiben. Nur ein geringer Anteil (Willkürbewegungen) ist bewußt an die Außenwelt gerichtet, die meisten Steuerungsaufgaben (z.B. der Aufmerksamkeit) werden zum großen Teil unbewußt erledigt.
Vernetzung
Für die spezifischen Erregungen der Pyramidenzellen gilt wie an vielen Stellen des Nervensystems das Konvergenz-Divergenz-Prinzip welches besagt, dass jede Zelle von vielen anderen erregt wird und selbst an viele andere Nervenzellen Impulse sendet. So ist jedes Teil der Hirnrinde über den „Balken“ mit einem spiegelbildlichen Teil der anderen Hirnhemisphäre verbunden, aber die Pyramidenzellen bilden auch weit verfächerte Verbindungen in der gleichen Seite, Verbindungen zum Kleinhirn, Stammhirn usw.
Das Wachstum dieser unzählbaren, unüberschaubaren Verbindungen und die Ausbildung der synaptischen Kontakte zwischen den Pyramidenzellen findet besonders stark in den ersten Monaten und Jahren statt, es ist das Wachstum der neuronalen Netze, die seit der Beschreibung durch Donald O. Hebb als Träger der Gedächtnisfunktion angesehen werden.
Das Ergebnis dieser Aktivität sind „Gestalten“ von neuronalen Netzen, die zunächst als invariante Muster in den flüchtigen Erregungskomplexen erscheinen und dann durch verstärktes synaptisches Wachstum fixiert werden.
Fritz Mauthner zu Ehren
Vor circa hundert Jahren traten zwei Philosophen mit einer Sprachkritik an die Öffentlichkeit, Fritz Mauthner und Ludwig Wittgenstein. Während Wittgenstein durch seinen Lehrer Bertrand Russell angeregt wurde, sich mit den Grundfragen der Logik zu beschäftigen, erhielt Mauthner bei seinem Lehrer Ernst Mach in Prag die speziellen Grundlagen für spätere Arbeiten. Ernst Mach war als Physiker, Philosoph und Wissenschaftstheoretiker ein vielseitiger Forscher, der auch Sinnesphysiologie und Psychologie in seine Überlegungen einbezog und bereits vor A. Einstein das vierdimensionale Raum-Zeit-Kontinuum forderte. E. Mach gilt auch als Wegbereiter der psychologischen „Gestalttheorie“.
Sein Schüler Fritz Mauthner war ebenso breitgefächert interessiert und setzte sich in wissenschaftstheoretischen Betrachtungen mit den aktuellen Ergebnissen der Psychologie auseinander. Von E. Mach übernahm F. Mauthner die Vereinigung der Raumdimensionen und der Zeitdimension im vierdimensionalen Kontinuum. Während Albert Einstein diese Sichtweise auf den ganzen Kosmos anwendete, verknüpfte Mauthner diese moderne Ansicht mit psychophysiologischen Betrachtungen, die im Gedächtnis eine raumzeitliche Ordnung vermuten.
Zitat: „Wir werden die Zeit als die vierte Dimension des Wirklichen kennen lernen. In Anknüpfung daran wird es uns umso schneller einleuchten, daß unser Gedächtnissinn einzelne vergangene Vorstellungen, die sogenannten Erinnerungen, genau ebenso in der Zeit lokalisiert, wie unser Gesichtssinn seine Vorstellungen in den drei Dimensionen des Raumes lokalisiert. Und genau so wie der Schnittpunkt des Koordinatensystems für unsere Augen durch unser Gehirn geht, so ist der Nullpunkt für die Erstreckung der Zeit immer unsere Gegenwart; der Nullpunkt bleibt bei uns, während wir in der Zeit weiterleben, wie das Koordinatensystem des Raumes sich mit uns bewegt. Die begriffliche Schwierigkeit läge nur darin, daß das Gedächtnis uns die Zeit erst erzeugt, in welche es die Daten der übrigen Sinne projiziert.“
Mauthner schlug hier einen gedanklichen Weg ein, der den zeitlichen Aspekt der „Korrelationstheorie der Hirnforschung“, unseren „Arbeitstaktes im Bewußtsein“, bereits in das Blickfeld rückte.
Zitat:„Und so halte ich es für eine brauchbare Hypothese, daß allerdings immer nur eine Vorstellung an dem Nadelöhr unseres Bewußtseins vorüberzieht, weil ja in diesem Sinne immer nur das Gegenwärtigste, d. h. das im geistigen Magen eben sich Assimilierende, das eben augenblicklich dem Gehirn Arbeit machende — daß das allein die Aufmerksamkeit fesselt (natürlich, weil ja auch die Gegenwart als Zeit nur die Nadelspitze zwischen Vergangenheit und Zukunft ist, die Wirklichkeitswelt also in jedem Augenblick nicht breiter sein kann, als die Fadendünne dieses Augenblickes, als ein Nadelöhr), daß aber zugleich das Gedächtnis, d. h. die unbewußte Registratur des Gehirns, wohl über unseren ganzen Wissensschatz verfügt, alles mit der Augenblicksvorstellung zunächst Verwandte schon in Bereitschaft hält, also daß das Gehirn in seinem Gedächtnis den weiten Horizont besitzt, der die Welt der Erfahrung oder die Vergangenheit und die Welt der Möglichkeiten oder die Zukunft umfaßt.“ (Bewußtsein/Zeit und Assoziation)
Dem Gedächtnis kommt in Mauthners Sprachphilosophie eine fundamentale Bedeutung zu. Zitate:
„Meine Überzeugung ist, daß die Rätsel der Sprache mit dem Schlüsselworte Gedächtnis zu lösen seien, oder vielmehr daß die Rätsel, welche das Wesen und die Entstehung der Sprache uns aufgibt, zurückzuschieben seien auf das Wesen des menschlichen Gedächtnisses.“
„Bei dem normalen Menschen ist Sach- und Wortgedächtnis aufs engste miteinander verbunden. Ja diese Verbindung ist eine bloße Tautologie, wenn ich mit der Behauptung recht habe, daß die Sprache oder der Wortschatz eines Menschen eben nichts anderes sei als sein individuelles Gedächtnis für seine Erfahrung. Die Sprache ist nichts als Gedächtnis, weil sie gar nichts anderes sein kann.“'' (Gedächtnis und Sprache)
Gedächtnis, Bewußtsein und Sprache sind für Mauthner verschiedene Wörter für den ganzheitlichen Zusammenhang des Weltwissens aus einzelnen Erinnerungsbildern.
„Das Gedächtnis ist eine Tatsache des Bewußtseins und das Bewußtsein ist für uns nur als Gedächtnis eine Tatsache. Man könnte mit diesen Worten noch weiter jonglieren und würde doch nicht einmal in dem skeptischen Sinne der Sprachkritik zu einer festen Definition der beiden Begriffe gelangen. Wir ahnen jedoch, daß eine durch Selbstbeobachtung ermittelte Tatsache des Bewußtseins nicht das Abstraktum Gedächtnis ist, sondern nur die Reihe einzelner Erinnerungsbilder; wir ahnen, daß das Wort Bewußtsein eigentlich nichts anderes bedeutet als den Zusammenhang der Erinnerungsbilder(Bewußtes Gedächtnis)
Angeregt durch die Gestalttheorie stellte Mauthner den Begriff der „Ähnlichkeit“ in das Zentrum seiner erkenntnis- und sprachtheoretischen Betrachtungen.
Zitate:„Die Ähnlichkeit dürfte noch einmal die wichtigste Rolle in der Psychologie spielen. Vielleicht hat man die Ähnlichkeit bisher instinktiv darum vernachlässigt, weil man sonst zu früh hätte einsehen müssen, wie tief unser logisches oder sprachliches Wissen unter unseren wissenschaftlichen Ansprüchen stehe, wie weit entfernt unsere Begriffsbildung von mathematischer Genauigkeit sei; denn unsere Sprachbegriffe beruhen auf Ähnlichkeit, die mathematischen Formeln auf Gleichheit“
„Absolute Gleichheit ist eine Abstraktion des mathematischen Denkens. In der Wirklichkeitswelt gibt es nur Ähnlichkeit. Gleichheit ist starke Ähnlichkeit, ist ein relativer Begriff.“
„Auf Ähnlichkeit, nicht auf Gleichheit ist alles Klassifizieren oder die Sprache aufgebaut, auf Ähnlichkeit, nicht auf Gleichheit all unser Urteilen oder die Anwendung der Sprache. Alle Logik aber, auch die Algebra der Logik, geht von dem mathematischen Begriff der Gleichheit aus und ist darum eine gefährliche Wissenschaft. Um nicht zu weit abzuschweifen, sei nur kurz erwähnt, daß auch der Begriff oder das Gefühl der Kontinuität aus dem Gefühle der Ähnlichkeit allein entsteht.“''
Nach Mauthner ist die Sprache zwar gut geeignet zur Kommunikation, jedoch nicht zu Erkenntnissen von Wahrheit oder Wirklichkeit. Mit Namen und Gestalten lernt der Mensch nur den „Schleier der Maya“ kennen, aber nicht die dahinter verborgene Realität, dazu sind seine Sinnesorgane nicht geeignet.
Fritz Mauthner hatte sein Studium (Rechtswissenschaft) nicht abgeschlossen und schrieb neben philosophischen Büchern auch Romane und Zeitungsartikel, er galt als „Freigeist“ und „enfant terrible“ in der Wissenschaft. In der Auseinandersetzung mit anderen Meinungen war er immer geistreich, mitunter auch polemisch. Dementsprechend hatte er wenig Einfluß auf die Sprachwissenschaft und die Philosophie, aber seine gedanklichen Leitlinien weisen in eine Richtung, die hier aufgenommen und weitergeführt wurde.
Nachtrag 2009
"Eine Aussage kann nicht nur wahr, falsch oder sinnlos sein, sondern auch imaginär." (George Spencer-Brown: Laws of Form)
Die Neurolinguistik zielt darauf hin, eine naturalistische Erklärung für den Zusammenhang von sprachlichen Tätigkeiten mit der Gehirntätigkeit zu entwickeln. Sie ist jedoch davon weit entfernt in einer mißlichen Lage, solange von den beiden Seiten, der Hirnforschung und der Linguistik, kaum Verbindungsmöglichkeiten für eine tragfähige Brückenbildung bereitstehen.
Genau das ist der Fall:
Die Hirnforscher haben keine übergeordnete Theorie, mit der sie die sprachlichen Vorgänge begreifen können und sie begnügen sich vielfach darin, mit bildgebenden Verfahren die Stellen im Gehirn zu markieren, die z.B. bei bestimmten Aufgabestellungen erhöhten Stoffwechsel zeigen.
Es ist jedoch unmöglich, aus diesen Stoffwechsel-Bildern auf die geistigen Vorgänge zu schließen, die bei der Untersuchung im Kopf der Person ablaufen.
Eine einfache Überlegung kann das verdeutlichen: Es ist sicher richtig, daß bei jeder konzentrierten geistigen Aktion Energie zur Aktivierung von ausgewählten Nervenzellen benötigt wird.
Ebenso richtig ist aber auch, daß noch viel mehr Energie im gleichen Augenblick zur aktiven Hemmung der Nervenzellen, die nicht an der Aktion beteiligt sind, gebraucht wird. Aus den bunten Bildern der Gehirnforschung läßt sich nicht unterscheiden, ob der erhöhte Stoffwechsel durch erregende oder hemmende Vorgänge hervorgerufen wird.
Die Entwicklung von „gedankenlesenden Techniken“, die durch manche Medien geistert, kann zur Zeit nicht realistisch betrieben werden, dazu fehlt jede Grundlage.
Es fehlt den Hirnforschern auch die Grundlage für eine sinnhaltige Kommunikation mit den Sprachwissenschaftlern: eine gemeinsame Sprache!
Das Linguistik-Studium verwendet heute unendliche Bemühungen für den Aufbau einer ausgefeilten Sprachbarriere, hinter der die Insider unbekümmert die menschliche Sprache auf formal-logische Schemata reduzieren. Sie betreiben damit scharfsinnige Denkspiele, die zu nichts anderem verpflichten als zur Einhaltung der selbstgewählten Spielregeln. Daraus bilden sie lange Ketten ebenso evidenter wie trivialer Aussagen. Über Sprache erfahren wir dabei nichts Neues.

Als Ergänzung zu unseren Ansichten über Sinn und Sprache kann aber ein Blick über die Grenzen dienen, z.B. ein Blick in die Systemtheorie des Soziologen Niklas Luhmann (1927-1998), so wie er sich beim Googln ergeben kann.
N. Luhmann war ein „transdisziplinärer“ Soziologe, der Kommunikation als Essenz der Gesellschaft verstand und dem „Sinn“-Begriff dabei eine bedeutende Stellung einräumte ("Sinn ist laufendes Aktualisieren von Möglichkeiten").
In Anlehnung an den Mathematiker George Spencer-Brown betonte Luhmann die Beobachtung, und damit das Phänomen „Unterscheidung“ als elementare Vorgänge der Wahrnehmung, Klassifizierung und Benennung.
Der Leser erinnert sich an die hier bereits stark hervorgehobene erkenntnistheoretische Bedeutung von Grenzen. Aus unterscheidenden Grenzen erschien uns das „ungeheures Geflecht der Sprache“ (Humboldt) zu wachsen, und unsere Ansicht erhält interdisziplinäre Unterstützung, wenn sie im Einklang mit N.Luhmanns vielbeachteter und vieldiskutierter „System-Theorie“ steht.
Unter einem System versteht Luhmann einen Funktionszusammenhang, welcher sich durch seine Abgrenzung von der Umwelt selbst im Zustand einer bestimmten Ordnung hält. Ein System muß demnach primär zur aktiven Erzeugung und Gestaltung von speziellen Grenzen fähig sein.
Psychische und soziale Systeme konstituieren sich für Luhmann als Sinnzusammenhänge. Der Sinnbegriff umfaßt jegliche Ordnungsform menschlichen, bewußten Erlebens; es gibt demnach kein sinnloses Erleben.
Nach der „Systemtheorie“ konstruieren unsere Sinnesorganen und das Nervensystem ein „Bild“ der Welt allein aus speziellen Formen von Unterscheidungen, aus variablen Gestaltungen von Grenzen. Die Welt ist viel zu komplex, um von einem System erfaßt zu werden. Deshalb ist nach Luhmann das konstruierte „Bild“ der Welt immer eine Vereinfachung, eine Reduktion der unendlichen Komplexität auf ein überschaubares Maß.
An Stelle der äußeren Weltkomplexität erzeugt das System „Mensch“ eine innere Ordnung. Dieses Geschehen versteht Luhmann als Sinnbildung. Das Komplexitätsgefälle wird vom System in der Form eines subjektiven Weltentwurfs, der die äußere Welt reduziert, ausgeglichen. Das System interpretiert die Welt selektiv und reduziert damit die Komplexität auf das ihm zugängliche Maß hin. Dadurch ermöglicht es sich strukturierte Möglichkeiten des eigenen Erlebens und Handelns.
Sinn tritt immer in abgrenzbaren Zusammenhängen auf und verweist zugleich über den Zusammenhang, dem er angehört, hinaus; er macht andere Möglichkeiten vorstellbar und genau hierin liegt nach Luhmann die Funktion der Sinnbildung. Sinn ist in Luhmanns Sicht „die Einheit der Differenz von Aktualität und Potentialität“
Kommunikation konstituiert immer Sinn, ist aktuelle Selektion aus der Potentialität aller zuvor gegebenen Möglichkeiten.
Sinn reguliert nach Luhmann die selektive Erlebnisverarbeitung, ist die selektive Beziehung zwischen System und Welt. Sinn ermöglicht gleichzeitig die Reduktion und Erhaltung von Komplexität.
Sinn läßt sich demnach verstehen als Prämisse der Erlebnisverarbeitung. Sinn ermöglicht dem Bewußtsein eine Auswahl und verweist über das Gewählte auf das Nichtgewählte und somit auf die Grenzenlosigkeit der Welt.
Kommunikation kann nach dieser Terminologie keine Übertragung von Sinn oder von Informationen sein, sondern Kommunikation ist gemeinsame Aktualisierung von Sinn, die mindestens einen der Teilnehmer informiert.
Dieser knappe Überblick über die Grundlagen der Luhmannschen Systemtheorie mag genügen, um deren Parallelen zu den hier beschriebenen Anschauungen hervorzuheben.
Die Gemeinsamkeiten zeigen sich in der Auslegung von „Sinn“, der als eine komprimierte Darstellung der Welt-Komplexität im Bewußtsein verstanden wird, sowie in der Bedeutung von variablen Grenzbildungen bei der Konstruktion von Unterscheidungen und Entscheidungen, bei der ständigen Erzeugung, Veränderung und Erweiterung von „Sinn“.
Luhmanns Konstruktion der „Sinn-Einheit“, in der eine ständig wechselnde Selektion zur Aktualisierung von Teilgebieten führt, erscheint mit dem Gedanken an eine dafür benötigte Konstruktionsvorschrift (Algorithmus) nach dem Modell der Mandelbrotmenge, deren komplexe Grenzstruktur den neuronalen Netzen im Cortex mit Hilfe eines „Gehirnschrittmachers“ eine Gestalt verleiht, durchaus vereinbar.
Schlusswort

„Kein einzelner kann hoffen, ein so ungeheures Gebiet ganz zu bearbeiten; dies kann nur den aufeinander folgenden Bemühungen vieler gelingen, die sich einander berichtigen und ergänzen. Am wenigsten könnte ich, und unter den Umständen, unter welchen ich diese Blätter beginne, mir schmeicheln, irgend etwas Vollständiges zu leisten. Es hat mir nur besser geschienen, selbst Hand an den Versuch zu legen, als bloß einen Entwurf dazu vorzuzeichnen. Sowohl die aufstoßenden Schwierigkeiten, als die sich ergebenden Vorteile zeigen sich besser, wenn man den Weg selbst zu gehen unternimmt, als wenn man sich bloß ihn von einer Anhöhe zu übersehen versucht.“
Wilhelm von Humboldt (aus: Thesen zur Grundlegung einer Allgemeinen Sprachwissenschaft,14 )
Literatur
- Klaus, Georg: Philosophisches Wörterbuch, Dietz Verlag Berlin 1968
- Hartmann, Nicolai: Teleologisches Denken, Walter de Gruyter 1966
- Hassler, Rolf: Regulation der psychischen Aktivität, in: „Hirnforschung und Psychiatrie“ Colloquium Verlag, Berlin 1971
- Humboldt, Wilhelm v.: Schriften zur Sprache, Reclam Verlag 1973
- Koch, Christof: Bewusstsein - ein neurobiologisches Rätsel, dt. Spektrum Verlag 2005 (engl. 2004; sehr gründliche Einführung in die Arbeitsweise des Gehirns; über Feuerraten und Oszillationen: S. 38f.)
- Lauwerier, Hans: Fraktale verstehen und selbst programmieren, Wittig Fachbuch 1989
- Luria, Alexander Romanowitsch: Die höheren kortikalen Funktionen des Menschen und ihre Störungen bei örtlichen Hirnschädigungen, VEB Deutscher Verlag der Wissenschaften Berlin 1970
- Mandelbrot, Benoît B.: Die fraktale Geometrie der Natur, Birkhäuser Verlag, Berlin 1991
- Mauthner, Fritz: Beiträge zu einer Kritik der Sprache
- Pöppel, Ernst: Grenzen des Bewußtseins, Deutsche Verlags-Anstalt 1985
- Pöppel, Ernst: 'Zeitlose Zeiten: Das Gehirn als paradoxe Zeitmaschine', in: Der Mensch und sein Gehirn, Piper-Verlag 1997
- Schnabel, Ulrich; Sentker, Andreas: Wie kommt die Welt in den Kopf?, Rowohlt 1997
- Singer, Wolf: 'Der Beobachter im Gehirn', in: Der Mensch und sein Gehirn, Piper-Verlag 1997
- Sucharowski, Wolfgang: Sprache und Kognition, Westdeutscher Verlag 1996
- Wiener, Norbert: Kybernetik, Rowohlt Verlag 1968
- Wooldridge, Dean E.: Mechanik der Gehirnvorgänge, R. Oldenbourg, Wien-München 1967
Lizenz
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 published by the Free Software Foundation; with no Invariant Sections, with no Front-Cover Texts, and with no Back-Cover Texts. In order to receive a copy of the GFDL GNU Free Documentation License write to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA or see http://www.gnu.org/copyleft/fdl.html.