Google Sheets-Kochbuch: Lösen von Gleichungen
Auf dieser Seite wird es mathematisch, das will ich Ihnen gar nicht verschweigen.
Lösen linearer Gleichungssysteme
[Bearbeiten]Ein lineares Gleichungssystem lässt sich erfreulicherweise leicht mit Hilfe der inversen Koeffizienten-Matrix lösen (sofern die Matrix invertierbar ist). Typische Beispiele beinhalten Gleichungssysteme mit zwei oder mit drei Unbekannten. Fangen wir mit zwei Unbekannten an.
| 1. | 2. | 3. | ||
|---|---|---|---|---|
|
|
wird umgeformt in |
|
führt zu den Koeffizienten |
|
Als erstes formen wir das Gleichungssystem so um, dass gleiche Variablen in der gleichen Spalte stehen. Die reinen Zahlen schreiben wir auf die rechte Seite der Gleichungen. Durch dieses Verfahren können wir die Koeffizienten leicht ablesen.

Das ist die Matrix A in A2:B3 und der Spaltenvektor B in C2:C3. Die Lösungen für die Variablen x und y ergeben sich jetzt, indem die Inverse der Matrix mit dem Spaltenvektor B multipliziert wird. Erfreulicherweise müssen wir uns jetzt nicht darum kümmern, wie man das macht, sondern lassen das Programm die Arbeit tun.
=MINVERSE(A2:B3)in E2- Berechnet das Inverse der Matrix (A-1).
=MMULT(E2:F3;C2:C3)in G2- Berechnet die Matrixmultiplikation des inversen der Matrix mit dem Spaltenvektor B.
Damit erhalten wir die Lösungen und . Man kann sich leicht davon überzeugen, dass diese Lösungen richtig sind, indem man sie in die ursprünglichen Gleichungen wieder einsetzt.
Lineares Gleichungssystem mit drei Unbekannten[1]
[Bearbeiten]| 1. | 2. | |
|---|---|---|
|
|
führt zu den Koeffizienten |
|
Stehen unsere Koeffizienten in dem Array A1:C3, und unser Spaltenvektor B in den Zellen D1:D3, erhalten wir die Lösungen mit:
=MMULT(MINVERSE(A1:C3);D1:D3)- x = 2,75
- y = -9
- z = -12,25
Lösen von quadratischen Gleichungen mit der pq-Formel
[Bearbeiten]Quadratische Gleichungen können mit Hilfe der pq-Formel gelöst werden. Dazu muss die Gleichung in Normalform vorliegen.
Die Lösungen ergeben sich mit der pq-Formel:
Das wäre ja im Prinzip einfach in der Tabelle einzugeben, ein Problem entsteht allerdings, da es - je nach Gleichung - keine, eine oder zwei reelle Lösungen gibt.
Es gibt keine (reelle) Lösung, wenn der Ausdruck unter der Wurzel (die sogenannte Diskriminante) negativ wird. Es gibt eine Lösung, wenn die Diskriminante 0 ist, es gibt zwei Lösungen, wenn die Diskriminante positiv ist.

=REGEXEXTRACT(A2;"(-?\s?\d+,?\d*)x")- Mit diesem regulären Ausdruck suchen wir nach einer rationalen Zahl, gefolgt von einem x. Das ist unser p.
- Die Gleichung steht in Zelle A2.
=REGEXEXTRACT(A2;"(-?\s?\d+,?\d*)\s?=")- Mit diesem regulären Ausdruck suchen wir nach einer rationalen Zahl, gefolgt von einem =. Das ist unser q.
=(B2/2)^2-C2- Berechnung der Diskriminante: p in der Zelle B2 und q in der Zelle C2.
=IFS(D2<0;0;D2=0;1;D2>0;2)- Bestimmung der Anzahl der Lösungen. In D2 wird die Diskriminante berechnet.
=IF(E2>0;-B2/2+SQRT(D2);"/")- Berechnung von x1. In E2 steht die Zahl der Lösungen.
- Wenn die Diskriminante größer als 0 ist, wird x1 berechnet. Ist die Diskriminante 0 macht es nichts, dass wir die Wurzel aus 0 noch einmal berechnen.
- Gibt es keine Lösung, geben wir / aus. Das kann man natürlich anpassen.
=IF(E2=2;-B2/2+sqrt(D2);"/")- Berechnung von x2, wenn es zwei Lösungen gibt.
| Gleichung | p | q | Diskriminante | Anzahl an Lösungen | x1 | x2 |
|---|---|---|---|---|---|---|
| x^2 + 3x - 4 = 0 | =REGEXEXTRACT(A2;"(-?\s?\d+,?\d*)x") |
=REGEXEXTRACT(A2;"(-?\s?\d+,?\d*)\s?=") | =(B2/2)^2-C2 | =IFS(D2<0;0;D2=0;1;D2>0;2) | =IF(E2>0;-B2/2+SQRT(D2);"/") | =IF(E2=2;-B2/2-SQRT(D2);"/") |
Zielwertsuche - Goal Seek-Add-on
[Bearbeiten]Mit einer Zielwertsuche berechnet man, welcher Eingabewert in einer Funktion zu einem gewünschten Ausgabewert führt. Es handelt sich um ein automatisiertes Ausprobieren der Eingabewerte, damit spart man sich das algebraisch möglicherweise schwierige oder langwierige (oder einfach nur nervige) Lösen einer Gleichung oder von Gleichungssystemen.
Die Zielwertsuche liefert immer nur ein Ergebnis. Gibt es also mehrere Lösungen zu einem Problem, wird trotzdem nur eine Lösung gefunden.
Die Zielwertsuche ist in Google Sheets über ein Add-on verfügbar, und funktioniert im Browser am PC oder einem Chromebook, nicht auf Mobilgeräten.
Add-on installieren
[Bearbeiten]- Öffnen Sie Google Sheets.
- Wählen Sie im Menü: Erweiterungen-> Add-ons -> Add-ons aufrufen
- Suchen Sie nach "Goal Seek for Sheets"
- Wenn Sie das Add-on gefunden haben, klicken Sie auf "Installieren".
- Sie müssen jetzt verschiedene Berechtigungen akzeptieren, bevor Sie das Add-on installieren können.
Goal Seek-Add-on verwenden
[Bearbeiten]- Wählen Sie im Menü: Erweiterungen -> Goal Seek -> Open
- Es öffnet sich das Add-on.
- Unter "Set Cell" tragen Sie die Zelle ein, in der das Endergebnis berechnet wird.
- In "To Value" tragen Sie die Zahl ein, die das Endergebnis erhalten soll.
- "By Changing Cell" wird die Zelle eingetragen, deren Wert verändert werden darf. Das ist typischerweise der Eingangswert für die Berechnung des Endergebnisses.
In den "Options" kann man eintragen, wieviele Berechnungsschritte vorgenommen werden dürfen, wie genau das Ergebnis am Zielwert liegen soll und wie lange die Berechnung insgesamt dauern darf.
Beispiel: Break-Even Analyse
[Bearbeiten]Bei der Herstellung eines Produktes ergeben sich bestimmte Fixkosten, außerdem Kosten, die durch die Anzahl der hergestellten Produkte bestimmt sind. Der Erlös ergibt sich aus der Anzahl der Produkte multipliziert mit dem Verkaufspreis. Der Gewinn ist gleich dem Erlös abzüglich der Kosten.
In unserem Beispiel betragen die Fixkosten 2.000,- €, die variablen Kosten 1,35 € pro Stück. Der Verkaufspreis beträgt 1,78 €. Gesucht ist die Stückzahl der Produkte, bei der der Break-Even-Point erreicht ist, also der Erlös so hoch ist wie die Kosten. Dann beträgt der Gewinn 0,00 €. Verkauft man mehr, wird der Gewinn positiv, verkauft man weniger, wird der Gewinn negativ.
Natürlich könnte man dieses einfache Beispiel auch durch Umstellen der Gleichungen lösen, aber die Kosten könnten ja deutlich komplizierter berechnet werden müssen, genauso der Erlös.

| Break-Even Analyse | |
|---|---|
| Stückzahl | 0 |
| Erlös | =B3*1,78 |
| Kosten | =2000+B3*1,35 |
| Gewinn | =B4-B5 |
- Unter Stückzahl tragen wir erst einmal nur eine 0 ein. Wenn man schon einen ungefähren Wert weiß sollte man allerdings damit anfangen, dann geht das Berechnen evtl. schneller.
- Die Zielzelle ist hier B6. Dort steht die Berechnung des Gewinns.
- Der Gewinn soll 0 betragen, das ist die Definition des Break-Even Punktes. Dieser Zielwert wird im Add-on unter "To Value" eingetragen.
- Geändert werden kann die Stückzahl. Diese steht in Zelle B3.
Klickt man nun auf "Solve", wird die Stückzahl solange verändert, bis der Zielwert von 0 erreicht ist. Das dauert leider, man kann dem Add-on dabei zuschauen.
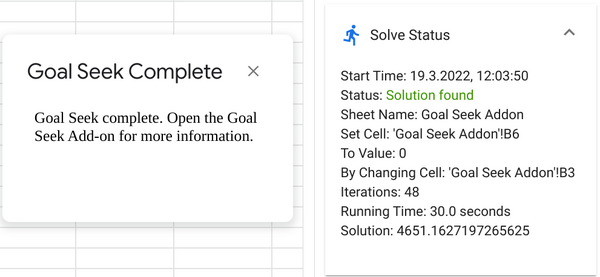
Die Lösung wird in Zelle B3 angezeigt. Bei etwas mehr als 4651 Stück wird der Break-Even Punkt erreicht.
Die Beispiele auf dieser Seite wurden getestet: 03/2022









