Mathe für Nicht-Freaks: Analysis 2/Integration durch Substitution in mehreren Dimensionen

Integration durch Substitution in 2 Dimensionen

• Sei ein Skalarfeld z(x;y) gegeben, und angenommen bzgl. irgendeines Kontextes wollten wir unbedingt wissen, wie groß das Volumen "zwischen" der Menge A in der xy-Ebene und der darüber liegenden Funktion z(x;y) ist. Z.B.

  

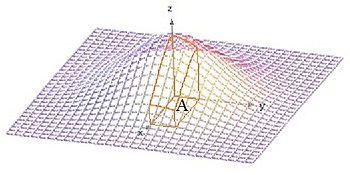
  ein volumenintegral

(besseres ZAHLENbeispiel auswählen, eins wo A begrenzt ist und wo die Berechnung durch Integration durch Substitution tatsächlich einfacher wird)

Dh. angenommen wir suchen

$\int _{A}z(x,y)\,\mathrm {d} x\mathrm {d} y=?$

.

• Während man nun überlegt, wie man das Volumen bzw. Integral berechnen soll, könnte man sich zwischendrin mal vorstellen, wie man das Volumen bzw. allgemein die Funktion nimmt und ein wenig entlang der xy-Ebene 'kontinuierlich' verformt, um ihr vielleicht eine einfachere Gestalt zu verleihen (bspbild einfügen).

Beschreiben kann man eine solche Verformung einfach durch eine Abbildung

$Q:A\subset \mathbb {R} ^{2}\rightarrow B\subset \mathbb {R} ^{2}:(x,y)\mapsto (a(x,y),b(x,y))$

. Z.B.

Die Abb. zeigt bsp.haft wie die Grundfläche einer Funktion z(x;y) verformt würde wenn mann statt x und y f(x,y) und g(x;y) substituieren würde.

. (Grafik an oben erwähntes besseres Beispiel anpassen, evtl. auch animieren)

Eine beliebige Verformung der Funktion z(x;y) wäre also gegeben durch eine Funktion der Form z(a(x;y);b(x;y)).

• Eine derartige Verformung des Volumens erscheint auf den ersten Blick vielleicht ziemlich sinnlos, schließlich verändert man es dabei ja. Aber, anstatt einfach rück zu verformen könnte man nun auf die Idee kommen einfach das Höhenprofil des Volumens zu verändern, damit es wieder die richtige Größe hat.

Genauer: durch die Verformung wurden, wie man ja an der Animation sehen kann, die Grundflächen der Quader verändert, die bei der Integration zur Berechnung des Volumens verwendet werden. Nun könnte man einfach, anstatt rückzuverformen, für jeden Quader die Höhe, sprich den Wert Z(x;y) so verkleinern, wie die Grundfläche des Quaders vergrößert wurde und umgekehrt. So würden die Quader ihre Größe beibehalten und das gesuchte Volumen konstant bleiben.

Und wenn man die Grundflächen dann infinitesimal klein werden lässt, sollte man praktisch für jeden Punkt der neuen Gesamtgrundfläche einen solchen "Verkleinerungsfaktor" c angeben können. Sprich eine Funktion c(x;y) finden können, sodass wir später eine neue allgemeine Gleichung der Form:

$\int _{A}z(x;y)\,\mathrm {d} x\mathrm {d} y=\int _{T(A)}c(x;y)\cdot z(a(x;y);b(x;y))\,\mathrm {d} x\mathrm {d} y$

haben sollten. T(A) meint die Gesamtgrundfläche nach der Verformung.

• Versuchen wir uns also mal zu überlegen, wie der "Vergrößerungsfaktor" (je nach dem!) c(x;y) in der Gleichung allgemein aussehen müsste. Zuerst ist dabei folgende Erkenntniss sehr wichtig: wenn man a(x;y) und b(x;y) in z(x;y) einsetzt, wird z(x;y) nicht so verformt wie die Abbildung
  $Q:\mathbb {R} ^{2}\rightarrow \mathbb {R} ^{2}:(x,y)\mapsto (a(x,y),b(x,y))$

A verformt sondern so wie die Umkehrabbildung $Q^{-1}$ A verformt. Denn der Punkt, nennen wir ihn (x';y') und der dazugehörige Wert Z(x';y') befinden sich nach der Verformung nicht an dem Punkt Q(x';y') sonder an dem Punkt $Q^{-1}(x';y')$, denn

$Z(Q(Q^{-1}(x';y')))=Z(x';y')$ und nicht $Z(Q(Q(x';y'))=Z(x';y')$.

• Um die bei der Verformung mit verformten Quader wieder auf ihr ursprüngliches Volumen zu bringen, wollen wir uns nun also fragen: Um welchen Faktor vergrößert $Q^{-1}$ ein kleines Grundflächenquadrat?

Denn um diesen Faktor würde sich auch das Volumen des entsprechenden Quaders vergrößern, weshalb wir seine Höhe Z(x';y') später um diesen Faktor verkleinern müssten, um ihn wieder auf sein Ursprungsvolumen zu bringen.

• Antwort: zur geistigen Unterstützung betrachte man nochmal

  

  .

Obda. sei nun

$Q^{-1}:\mathbb {R} ^{2}\rightarrow \mathbb {R} ^{2}:(x,y)\mapsto (a(x,y),b(x,y))$

. Wir wollen obda. wissen wie groß das Bild eines kleinen Quadrats gegeben durch $\Delta x\cdot \Delta y$ am Punkt (x';y') unter Q^(-1) ist. Wie man sieht würde eine genaue Berechnung sehr kompliziert werden, da die Linien nicht gerade verlaufen. Aber je kleiner man das Quadrat $\Delta x\cdot \Delta y$ wählt, desto gerader werden ja auch die Ränder des Bildquadrats unter Q^(-1) und desto genauer sollte auch eine Abschätzung des Flächeninhalts über die beiden tangential an Q^(-1)(x';y') anliegenden Bildvektoren und deren aufgespannten Parallelogramm sein (siehe Grafik). Außerdem wollen wir die Quadrate am Ende ja eh infinitesimal klein werden lassen, und auf dieser Ebene sollte diese Abschätzung nicht nur eine Abschätzung sein, sondern exakt. Die beiden tangentialen Bildvektoren vom Punkt (x':y') wären also gegeben durch:

${\vec {v}}_{x}(x';y')=\partial _{x}{\begin{pmatrix}a(x;y)\\b(x;y)\end{pmatrix}}_{\begin{pmatrix}x'\\y'\end{pmatrix}}\cdot \Delta x$ und ${\vec {v}}_{y}(x';y')=\partial _{y}{\begin{pmatrix}a(x;y)\\b(x;y)\end{pmatrix}}_{\begin{pmatrix}x'\\y'\end{pmatrix}}\cdot \Delta y$.

• An dieser Stelle könnte einem eine kleine Idee einfallen: So wie Q^(-1) ein Quadrat vergrößert, so verkleinert Q dieses Quadrat. Dh. anstatt später mit dem Kehrwert des Vergrößerungsfaktors von Q^(-1) zu multiplizieren, sollten wir auch direkt mit

dem Vergrößerungsfaktor von Q multiplizieren können. So sollte sich ein gegenwärtig absehbarer Bruchterm für c(x';y') vermeiden lassen. Wenn wir die Benennung ändern zu

$Q:\mathbb {R} ^{2}\rightarrow \mathbb {R} ^{2}:(x,y)\mapsto (a(x,y),b(x,y))$

werden die beiden tangentialen Bildvektoren wieder durch obige Terme gegeben sein.

• Um den Flächeninhalt des entsprechenden Parallelogramms zu berechnen, kann man sich nun einfach des Kreuzprodukts in 3 Dimensionen bedienen:

$\vert {\begin{pmatrix}\partial _{x}a(x;y)\\\partial _{x}b(x;y)\\0\end{pmatrix}}\cdot \Delta x\times {\begin{pmatrix}\partial _{y}a(x;y)\\\partial _{y}b(x;y)\\0\end{pmatrix}}\cdot \Delta y\vert _{\begin{pmatrix}x'\\y'\end{pmatrix}}=...=\vert {\begin{pmatrix}0\\0\\(\partial _{x}a(x;y)\cdot \partial _{y}b(x;y)-\partial _{y}a(x;y)\cdot \partial _{x}b(x;y))\cdot \Delta x\Delta y\end{pmatrix}}\vert _{\begin{pmatrix}x'\\y'\end{pmatrix}}$

Dh. der Vergrößerungsfaktor sollte einfach

$(\partial _{x}a(x;y)\cdot \partial _{y}b(x;y)-\partial _{y}a(x;y)\cdot \partial _{x}b(x;y))_{\begin{pmatrix}x'\\y'\end{pmatrix}}$

sein. Und die Formel damit

$\int _{A}z(x;y)\,\mathrm {d} x\mathrm {d} y=\int _{Q^{-1}(A)}z(a(x;y);b(x;y))(\partial _{x}a(x;y)\cdot \partial _{y}b(x;y)-\partial _{y}a(x;y)\cdot \partial _{x}b(x;y))\,\mathrm {d} x\mathrm {d} y$

lauten.

"Symmetrien ausnutzen"

• Mal angenommen bzgl. irgenteines Kontextes müsste man ein Integral V der Form

berechnen, dh. ein Integral der Form

$V=\int _{A}z(x;y)\,\mathrm {d} x\mathrm {d} y$

wobei z(x;y) irgendeine zum Nullpunkt Radialsymmetrische 3D Funktion ist und A kreisförmig um den Nullpunkt gelegen ist.

• Bei dieser Gelgenheit könnte einem mal folgende Idee Einfallen: anstatt das Volumen V über ganz viele kleiner werdende Quader zu

approximieren (evtl. bild dazu einfügen) könnte man dieses Integral, dank seiner Form!, über dünner werdende 'Kreisscheiben' approximieren

.

• Und die Teilvolumina dieser 'Kreisscheiben' ließen sich ja auch ganz leicht berechnen: man stelle sich einfach vor, wie man eine solche nimmt und sie ausrollt. Dann hätte man einen flachen Quader mit der Höhe $\Delta r$ und der Grundfläche $2\pi r\cdot z(0;r)$, also das Teilvolumen $2\pi rz(0;r)\cdot \Delta r$. Dh. als Grenzwert sollte man einen Term der Form $lim_{\Delta r_{i}\rightarrow 0}\sum _{0\leq r_{i}\leq R}2\pi r_{i}z(0;r_{i})\cdot \Delta r_{i}$ bekommen, wobei R der Radius der Grundfläche A ist.
• In solchen Situationen erhält man nun mit fast 100%iger Sicherheit das eigentlich gemeinte Integral immer indem man einfach ersetzt: $lim_{\Delta r_{i}\rightarrow 0}\sum _{0\leq r_{i}\leq R}2\pi r_{i}z(0;r_{i})\cdot \Delta r_{i}\to \int _{0}^{R}2\pi rz(0;r)\,\mathrm {d} r$. Dies könnte einen zu der Vermutung
  $V=\int _{A}z(x;y)\,\mathrm {d} x\mathrm {d} y=\int _{0}^{R}2\pi rz(0;r)\,\mathrm {d} r$

führen, unter den gemachten Vorraussetzungen!.

• ACHTUNG: bereits im Voraus, aber auch im Nachhinein können einem begründete Zweifel aufkommen. Denn die Formel für die Teilvolumen, die stimmt ja eigentlich gar nicht. Denn streng genommen könnte man diese Kreisscheiben egal wie dünn sie sind ja gar nicht zu einem dünnen Quader ausrollen, ohne ihr Volumen zu ändern. Und zwar aus dem gleichen Grund, aus dem man ein Blatt Papier auch nie faltenfrei auf einen Globus kleben könnte.
• Mithilfe der allgemeinen Formel zu Integration durch Substitution lässt sich aber zeigen, dass obige Vermutung bzw. Gleichung tatsächlich richtig ist. Der Gedanke, der hierbei den Durchbruch bringt, ist folgender: die Verformung der Funktion, von der oben bei der allgemeinen Formel ständig gesprochen wurde, wäre hier das Ausrollen der Kreisscheiben.

Man sollte sich also einfach nur die entsprechende Abbildung Q von B nach A überlegen müssen, in die Formel einsetzen und die vermutete Gleichung sollte sich ergeben.

Von B nach A und nicht von A nach B deshalb weil ja B die neue Fundamentmenge bzw. Definitionsmenge für unsere Funktion z(x;y) werden soll.

• Die entsprechende Abbildung wäre $Q:A\rightarrow B:(x,y)\mapsto (ysin({\frac {x}{y}}),ycos({\frac {x}{y}}))$. Einsetzen
  ${\begin{aligned}\int _{A}z(x;y)\,\mathrm {d} x\mathrm {d} y\,&=\,\int _{Q^{-1}(A)}z(a(x;y);b(x;y))\vert (\partial _{x}a(x;y)\cdot \partial _{y}b(x;y)-\partial _{y}a(x;y)\cdot \partial _{x}b(x;y))\vert \,\mathrm {d} x\mathrm {d} y=\\[0.3em]&=\,\int _{B}z(ysin({\frac {x}{y}});ycos({\frac {x}{y}}))\vert 1\vert \,\mathrm {d} x\mathrm {d} y=\\[0.3em]&=\,\int _{0}^{R}\mathrm {d} y\int _{-y\pi }^{y\pi }\mathrm {d} x\,z(ysin({\frac {x}{y}});ycos({\frac {x}{y}}))=\\[0.3em]&=\,\int _{0}^{R}\mathrm {d} y\int _{-y\pi }^{y\pi }\mathrm {d} x\,z(0;y)=\\[0.3em]&=\,\int _{0}^{R}2\pi yz(0;y)\,\mathrm {d} y\end{aligned}}$

• Im Nachhinein ist dieses Resultat wegen des bereits genannten Grunds sogar erstaunlich. Dies könnte einen auf eine weitere Idee bringen: wenn es scheinbar keine Rolle spielt, ob die Teilvolumen gekrümmt sind oder nicht, so könnte man über die Technik von gerade doch sicher noch eine Menge anderer Volumen ganz einfach approximieren und berechnen. So sollte man z.B., wenn das stimmt mithilfe der Formel für die Kugeloberfläche das Kugelvolumen berechnen können.
• Man betrachte hierfür eine Kugel mit Radius R. Die Oberfläche in abhänigkeit vom Radius r sei f(r). Nun unterteile man die Kugel einfach in mehrere Hohlkugeln mit möglichst kleiner Wandicke $\Delta r$.

  

Das Volumen der Wand wäre dann $f(r)\Delta r$, also Grundfläche mal Höhe. Und die Summe der Volumen der Wände sollte dann ungefähr das Kugelvolumen sein. Und je dünner man dann die Wände macht desto genauer sollte die Summe das Kugelvolumen approximieren, also $V(R)=lim_{\Delta r_{i}\rightarrow 0}\sum _{0\leq r_{i}\leq R}f(r_{i})\cdot \Delta r_{i}$.

• Die letzte Summe wäre das Integral $\int _{0}^{R}f(r)\,\mathrm {d} r$. Und das hieße nun, als bemerkenswerte Vermutung: die Ableitung des Kugelvolumens sollte die Kugeloberfläche sein.
• Diese Vermutung ist auch tatsächlich richtig. Als Anwendung könnten wir diese jetzt aber auch mit der Substitutionsformel für 3 Dimensionen beweisen. Die Formel für die Kugeloberfläche ist $4pi*r^{2}$. Die Vermutung ist also $\int _{K(R)}1\,\mathrm {d} x\mathrm {d} y\mathrm {d} z=\int _{0}^{R}4\pi r^{2}\,\mathrm {d} r$. Für den Beweis wollen wir uns wie beim ersten Anwendungsbeispiel die Verformung der Kugel, dh. das ausrollen der Kugelwände nochmal etwas genauer betrachten. Denn diese Verformung sollte und ja die Substitution Q geben.

Man schlage einfach die Formeln für Kugelvolumen und Kugeloberfläche nach. Allerdings, als Anwendungsbeispiel kann man dies auch aus der Substitutionsformel für 3 Dimensionen folgern, ohne die genauen Formeln für Kugelvolumen und Kugeloberfläche zu kennen.

• Die Substitutionsformel für 3 Dimensionen kann man sich analog zu der obigen Formel für 2 Dimensionen herleiten. Man findet
  $\int _{A}h(x;y;z)\,\mathrm {d} x\mathrm {d} y\mathrm {d} z=\int _{Q^{-1}(A)}h(a(x;y;z);b(x;y;z);c(x;y;z))\vert ({\begin{pmatrix}\partial _{x}a(x;y;z)\\\partial _{x}b(x;y,z)\\\partial _{x}c(x;y;z)\end{pmatrix}}\times {\begin{pmatrix}\partial _{y}a(x;y;z)\\\partial _{y}b(x;y;z)\\\partial _{y}c(x;y;z)\end{pmatrix}})\circ {\begin{pmatrix}\partial _{z}a(x;y;z)\\\partial _{z}b(x;y;z)\\\partial _{z}c(x;y;z)\end{pmatrix}}\vert \,\mathrm {d} x\mathrm {d} y\mathrm {d} z$

• Wir versuchen nun die Vermutung in Integralform zu formulieren. Hierzu brauchen wir:

Das Kugelvolumen in Integralform in abhängigkeit von r

$\int _{K(r)}1\,\mathrm {d} x\mathrm {d} y\mathrm {d} z$

wobei

$K(r)=\{{\vec {x}}\in \mathbb {R} ^{3}\mid \vert {\vec {x}}\vert \leq r\}$

. Und die Kugeloberfläche in Integralform in Abhängigkeit von r

$2\int _{A(r)}\,\mathrm {d} x\mathrm {d} y\vert {\begin{pmatrix}1\\0\\\partial _{x}z(x;y)\end{pmatrix}}\times {\begin{pmatrix}0\\1\\\partial _{y}z(x;y)\end{pmatrix}}\vert$

wobei

$z(x;y)={\sqrt {r^{2}-x^{2}-y^{2}}}$

und

$A(r)=\{{\vec {x}}\in \mathbb {R} ^{2}\mid \vert {\vec {x}}\vert \leq r\}$

. Die Vermutung lautet also

$\int _{K(R)}1\,\mathrm {d} x\mathrm {d} y\mathrm {d} z=\int _{0}^{R}\mathrm {d} r\int _{A(r)}\,\mathrm {d} x\mathrm {d} y2\vert {\begin{pmatrix}1\\0\\\partial _{x}z(x;y)\end{pmatrix}}\times {\begin{pmatrix}0\\1\\\partial _{y}z(x;y)\end{pmatrix}}\vert$

. Nur z(x;y) eingesetzt und umgeformt

$\int _{K(R)}1\,\mathrm {d} x\mathrm {d} y\mathrm {d} z=\int _{0}^{R}\mathrm {d} r\int _{A(r)}\,\mathrm {d} x\mathrm {d} y2{\frac {r}{\sqrt {r^{2}-x^{2}-y^{2}}}}$

• Die frage ist nun wieder: Welches Q müssten wir in die allgemeine Formel einsetzen, damit diese Gleichung gezeigt wird?

Schnell stellt man fest, dass die Frage ungleich schwerer ist als die Frage bei vorigem Bsp..

Betrachten wir deshalb vielleicht mal die beiden Definitionsmengen A;B der Integrale, schießlich wären dies ja die beiden Mengen die Q verformt. Scheinbar

Eine relativ nahe liegende Idee wäre nun den Kegel zur oberen Halbkugel zu verformen und das gleiche mit einem entsprechenden Kegel auf der Unterseite zu machen, indem man einfach die Kreisränder der Kegel nimmt und sie langsam parallel zur z Achse auf die xy Ebene verschiebt. Dh.

Man bemerke das diese Verformung nicht Volumenerhaltend wäre.

Zwar existiert auf dem ersten Bild auf der Unterseite keine Kegel, aber wenn man sichs genau überlegt sollte das keine Rolle spielen. Wir modifizieren die Vermutung einfach so, dass wir nur noch eine Halbkugel und einen Kegel betrachten müssen:

$\int _{0}^{R}\mathrm {d} r\int _{A(r)}\,\mathrm {d} x\mathrm {d} y{\frac {r}{\sqrt {r^{2}-x^{2}-y^{2}}}}={\frac {1}{2}}\int _{K(R)}1\,\mathrm {d} x\mathrm {d} y\mathrm {d} z=\int _{{\frac {1}{2}}K(R)}1\,\mathrm {d} x\mathrm {d} y\mathrm {d} z$

wobei (1/2)K(R) einfach für die Menge der oberen Halbkugel steht.

Die Abbildung die uns vorschwebt ist $Q:{\frac {1}{2}}T\rightarrow {\frac {1}{2}}K(R):(x,y,z)\mapsto (x,y,{\sqrt {z^{2}-x^{2}-y^{2}}})$. Einsetzen gemäß der Sub.formel für 3 dim. ergibt

$\int _{{\frac {1}{2}}K(R)}1\,\mathrm {d} x\mathrm {d} y\mathrm {d} z=\int _{{\frac {1}{2}}T}1\vert ({\begin{pmatrix}\partial _{x}a(x;y;z)\\\partial _{x}b(x;y,z)\\\partial _{x}c(x;y;z)\end{pmatrix}}\times {\begin{pmatrix}\partial _{y}a(x;y;z)\\\partial _{y}b(x;y;z)\\\partial _{y}c(x;y;z)\end{pmatrix}})\circ {\begin{pmatrix}\partial _{z}a(x;y;z)\\\partial _{z}b(x;y;z)\\\partial _{z}c(x;y;z)\end{pmatrix}}\vert \,\mathrm {d} x\mathrm {d} y\mathrm {d} z=...=\int _{{\frac {1}{2}}T}{\frac {z}{\sqrt {z^{2}-x^{2}-y^{2}}}}\,\mathrm {d} x\mathrm {d} y\mathrm {d} z=\int _{0}^{R}\mathrm {d} z\int _{A(z)}\,\mathrm {d} x\mathrm {d} y{\frac {z}{\sqrt {z^{2}-x^{2}-y^{2}}}}$

tatsächlich unsere gesuchte Vermutung.

• Eine neue Approximationsidee für die Fläche eines Kreises (bild). Die Ableitung des der Kreisfläche ist der Kreisumfang (bild)

Die dx;dy-Kalküle

• 1 dim. Substi. formel mittels dx;dy-Kalkül
• 2 dim. Subsi. formel mittel dx;dy-Kalkül
• Analoger Versuch für eine 3 dim. Substi. formel
• evtl. Formulierung einer allgemeinen Vermutung für n dim. (Transformationssatz)
• machen unbedingt einleuchtend und plausibel
  $\int _{\{a_{1}{\vec {x}}_{1}+...+a_{n}{\vec {x}}_{n}\mid a_{1};...;a_{n}\in [0;1]\}}1\,\mathrm {d^{n}} x=det({\vec {x}}_{1};...;{\vec {x}}_{n})$

wobei ${\vec {x}}_{1};...;{\vec {x}}_{n}\in \mathbb {R} ^{n}$

• wenn man einfach definiert
  $det({\vec {x}}_{1};...;{\vec {x}}_{n}):=\int _{\{a_{1}{\vec {x}}_{1}+...+a_{n}{\vec {x}}_{n}\mid a_{1};...;a_{n}\in [0;1]\}}1\,\mathrm {d^{n}} x$

, so sollte allegmein für n element N dimensionen gelten

$\int _{A\subset \mathbb {R} ^{n}}h(x_{1};...;x_{n})\,\mathrm {d^{n}} x=\int _{F^{-1}(A)}h(f_{1}(x_{1};...;x_{n});...;f_{n}(x_{1};...;x_{n}))det(\partial _{x_{1}}F;...;\partial _{x_{n}}F)\,\mathrm {d^{n}} x$