Mathe für Nicht-Freaks: Buchanfang Maßtheorie by Richard4321/ Quader- und Rechtecksfiguren

Wiederholung

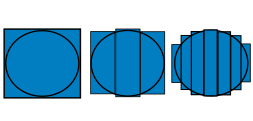
Um den Inhalt einer Fläche zu bestimmen, können wir diese von innen und von außen mit Rechtecken ausschöpfen bzw. überdecken:

• 
  Ausschöpfung eines Kreises mit Rechtecken
• 
  Überdeckung eines Kreises mit Rechtecken

Der Flächeninhalt jeder Ausschöpfung und Überdeckung ergibt sich aus den Flächeninhalten der jeweiligen Quaderfiguren. Dabei ist jede Ausschöpfung eine Abschätzung des tatsächlichen Flächeninhalts nach unten und jede Überdeckung eine Abschätzung nach oben. Kommt im Grenzwert bei der Ausschöpfung und der Überdeckung dasselbe heraus, so nennen wir diesen Grenzwert den Flächeninhalt.

In diesem Kapitel müssen wir die Eigenschaften der Quaderfiguren genauer betrachten, um den Jordan-Inhalt definieren zu können.

Quaderfiguren

Definition

Die Quaderfiguren definieren wir uns als endliche disjunkte Vereinigung von halboffenen Quadern.

$F^{p}:=\left\{\biguplus _{i=1}^{n}A_{i}:A_{i}\in I^{p}\right\}$

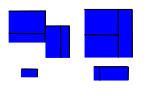
Inhaltsfunktion

Naheliegend ist, dass sie einer Quaderfigur (siehe das Bild)

durch Überlappung verringert sich das Volumen

die Summe der Flächen der Einzelquader zuordnet. Unsere Hoffnung ist, dass die Funktion wieder additiv wird, das ist ja die Zieleigenschaft für den Peano-Jordan-Inhalt..

Satz

$m:F^{p}\rightarrow [0,\infty ],\biguplus _{i=1}^{n}A_{i}\mapsto \sum _{i=1}^{n}m(A_{i})$

ist wohldefiniert und additiv.

Beweis

1.) Unabhängigkeit von der Darstellung: Wir müssen zeigen, dass die Abbildung wohldefiniert ist, d.h. wenn eine Quaderfigutr $A=\biguplus _{i=1}^{n}A_{i}\in F^{p}$ anders dargestellt wird durch $\biguplus _{j=1}^{k}B_{j}$ (durch mehr oder weniger Unterteilungen oder durch anders gewählte Unterteilungen, siehe das Bild), darf sich der Wert der Summe nicht ändern.

• 
• 

Das führen wir darauf zurück, dass wir die gemeinsame Verfeinerung der Unterteilungen betrachten

• 

und die Gleichheit der Summe dazu nachrechnen: Da der Schnitt zweier Quader wieder ein Quader ist Mathe für Nicht-Freaks: Buchanfang Maßtheorie by Richard4321/ Intervalle, Rechtecke und Quader gilt

$A_{i}=A_{i}\cap A=A_{i}\cap \biguplus _{j=1}^{k}B_{j}=\biguplus _{j=1}^{k}(A_{i}\cap B_{j})$

Nun wenden wir das auf den Quadern $I^{p}$ additive $m$ an und erhalten

$m(A_{i})=\sum _{j=1}^{k}m(A_{i}\cap B_{j})$

Aufsummiert über alle $i$ folgt

$\sum _{i=1}^{n}m(A_{i})=\sum _{i=1}^{n}\sum _{j=1}^{k}m(A_{i}\cap B_{j})$

Ganz analog wenden wir auf den einzelnen Quader

$B_{j}=B_{j}\cap A=B_{j}\cap \biguplus _{i=1}^{n}A_{i}=\biguplus _{i=1}^{n}(B_{j}\cap A_{i})$

das auf $I^{p}$ additive $m$ an und erhalten

$m(B_{j})=\sum _{i=1}^{n}m(B_{j}\cap A_{i})$

Aufsummiert über $j$ folgt

$\sum _{j=1}^{k}m(B_{j})=\sum _{j=1}^{k}\sum _{i=1}^{n}m(B_{j}\cap A_{i})$

Die rechte Seite kennen wir aber schon von oben und somit folgt

$\sum _{i=1}^{n}m(A_{i})=\sum _{j=1}^{k}m(B_{j})$

Damit ist die Summe unabhängig von der Darstellung von $A$ wohldefiniert.

2.) $m$ ist additiv: Die Summe ist gerade so konstruiert, dass $m$ additiv wird: Seien $A=\biguplus _{i=1}^{n}A_{i},B=\biguplus _{j=1}^{m}B_{j}\in F^{p}$ disjunkt. Einsetzen in $m$ ergibt

${\begin{array}{rcl}m(A\uplus B)&=&m(\biguplus _{i=1}^{n}A_{i}\uplus \biguplus _{j=1}^{m}B_{j})\\&{\stackrel {{\text{Def von }}m}{=}}&\sum _{i=1}^{n}m(A_{i})+\sum _{j=1}^{k}m(B_{j})\\&{\stackrel {{\text{Def von }}m}{=}}&m(\biguplus _{i=1}^{n}A_{i})+m(\biguplus _{j=1}^{m}B_{j})\\&=&m(A)+m(B)\end{array}}$

Differenz von Quaderfiguren ist eine Quaderfigur

Wir wollen Quaderfiguren vereinigen. Ggf. überschneiden sich dann die Figuren. Wir wollen die Vereinigung darstellen als disjunkte Vereinigung, weil nur für disjunkte Vereinigungen unser Inhalt additiv ist. Dafür benötigen wir die Differenz.

Satz

Die Differenz zweier Quaderfiguren ist eine Quaderfigur: Mit $A,B\in F^{p}$ gilt auch $A\backslash B\in F^{p}$.

Beweis

Wir formen die Differenz $A\backslash B$ um, um den letzten Satz des vorherigen Kapitels Mathe_für_Nicht-Freaks: Buchanfang_Maßtheorie_by_Richard4321/ Intervalle,_Rechtecke_und_Quader#Mehrfache_Differenz_von_Quadern anwenden zu können, den wir nur für diesen Zweck bewiesen haben und zwar

${\begin{array}{rcl}A\backslash B&=&\left(\biguplus _{i=1}^{n}A_{i}\right)\backslash \left(\biguplus _{j=1}^{m}B_{j}\right)\\&=&\biguplus _{i=1}^{n}\left(A_{i}\backslash \biguplus _{j=1}^{m}B_{j}\right)\end{array}}$

Jetzt wissen wir, dass die Elemente $A_{i}\backslash \biguplus _{j=1}^{m}B_{j}$ gemäß dem letzten Kapitel eine endliche disjunkte Vereinigung von Quadern sind, d.h. es gibt $C_{i1}\ldots ,C_{ik}\in I^{p}$ sodass

$A\backslash B=\biguplus _{i=1}^{n}\biguplus _{l=1}^{k}C_{il}$

und damit erhalten wir, dass $A\backslash B$ ein Element aus $F^{p}$ ist.

Vereinigung zweier Quaderfiguren ist eine Quaderfigur

Wir müssen die Vereinigung zweier Quaderfiguren darstellen als disjunkte Vereinigung von Quadern, dazu benötigen wir den letzten Satz über die Differenz von Quaderfiguren.

Satz

Die Vereinigung zweier Quaderfiguren ist eine Quaderfigur: Mit $A,B\in F^{p}$ gilt auch $A\cup B\in F^{p}$.

Beweis

Wir müssen $A\cup B$ als disjunkte Vereinigung von endlich vielen Quaderns schreiben, dazu formen wir um zu

$A\cup B=B\uplus A\backslash B$

Mit dem Satz darüber erhalten wir

$A\cup B=\biguplus _{j=1}^{m}B_{j}\uplus \left(\biguplus _{i=1}^{n}\biguplus _{l=1}^{k}C_{il}\right)$

und haben die gewünschte Darstellung.

Folgerungen für den Inhaltsbegriff

To-Do:

Additivität des Inhalts

Aus diesen Erkenntnissen können wir Eigenschaften unserer Inhaltsfunktion auf Quaderfiguren folgern, welche sich mit unserem intuitiven Begriff eines Inhalts decken:

• Der Inhalt ist monoton: Ist eine Menge A Teilmenge einer anderen Menge B, so muss der Inhalt von A kleiner oder gleich dem Inhalt von B sein.

A als Teilmenge von B

• Der Inhalt ist subadditiv: Bei Überschneidung von zwei Flächen A und B ist die Gesamtfläche kleiner als die Summe der Einzelflächen.

Der Schnitt von zwei Rechtecken

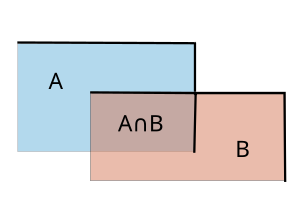
Monotonie des Inhaltes auf Quaderfiguren

Jetzt können wir ganz einfach die Monotonie des Inhaltes auf den Quaderfiuguren beweisen.

Satz

Seien $A,B\in F^{p}$. Dann gilt: $m$ ordnet größeren Mengen einen größeren Wert zu (Monotonie):

${\text{Für }}A\subseteq B{\text{ gilt }}m(A)\leq m(B)$

Beweis

Die Menge $B$ lässt sich darstellen, als der Teil in $A$ und der Teil außerhalb von $A$. Wir erhalten eine disjunkte Vereinigung

${\begin{array}{rcl}B&=&(B\cap A)\uplus (B\cap A^{C})\\&{\stackrel {A\subseteq B}{=}}&A\uplus (B\backslash A)\\&\geq &m(A)\end{array}}$

Darauf $m$ angewendet ergibt mit der Additivität

${\begin{array}{rcl}m(B)&=&m((B\backslash A)\uplus A)\\&{\stackrel {m{\text{ additiv}}}{=}}&\underbrace {m(B\backslash A)} _{\geq 0}+m(A)\\&\geq &m(A)\end{array}}$

Subadditivität des Inhalts auf Quaderfiguren

Wir wollen erreichen, dass unser Peano-Jordan-Inhalt additiv wird. Dafür benötigen wir folgende Ungleichung.

Satz (Eigenschaften von Inhalten: Subadditivität)

Seien $A_{i}\in F^{p}$ mit $i\in \mathbb {N}$ und $m$ ein Inhalt. Dann gilt: Die Fläche einer endlichen Vereinigung von Quaderfiguren ist kleiner gleich der Summe der Einzelflächen:

$m\left(\bigcup _{i=1}^{n}A_{i}\right)\leq \sum _{i=1}^{n}m(A_{i})$

Beweis (Eigenschaften von Inhalten: Subadditivität)

Um die Additivität von $m$ ausnutzen zu können, machen wir die Vereinigung künstlich disjunkt und verwenden dann die Monotonie:

Die zweifache Vereinigung $A_{1}\cup A_{2}$ lässt sich darstellen als die Elemente, die in $A_{1}$ sind und die Elemente, die in $A_{2}$, aber nicht $A_{1}$ sind. Man erhält eine disjunkte Vereinigung:

$A_{1}\cup A_{2}=A_{1}\uplus (A_{2}\backslash A_{1})$

Die dreifache Vereinigung $A_{1}\cup A_{2}\cup A_{3}$ lässt sich darstellen als die Elemente, die in $A_{1}$ sind, als die Elemente, die in $A_{2}$, aber nicht $A_{1}$ sind und als die Elemente, die in $A_{3}$, aber nicht in $A_{1}$ oder $A_{2}$ sind. Man erhält eine disjunkte Vereinigung:

${\begin{aligned}A_{1}\cup A_{2}\cup A_{3}=A_{1}\uplus (A_{2}\backslash A_{1})\uplus (A_{3}\backslash (A_{1}\cup A_{2}))\end{aligned}}$

Die $n$-fache Vereinigung lässt sich dann als disjunkte Vereinigung darstellen durch

$\bigcup _{i=1}^{n}A_{i}=A_{1}\uplus \biguplus _{i=2}^{n}\left(A_{i}\backslash \bigcup _{j=1}^{i-1}A_{j}\right)$

Nun lässt sich $m$ anwenden und die Additivität ausnutzen:

${\begin{array}{rcl}m\left(\bigcup _{i=1}^{n}A_{i}\right)&=&m\left(A_{1}\uplus \biguplus _{i=2}^{n}\left(A_{i}\cap \bigcup _{j=1}^{i-1}A_{j}^{C}\right)\right)\\&{\stackrel {m{\text{ additiv}}}{=}}&m(A_{1})+\sum _{i=2}^{n}m\left(A_{i}\backslash \bigcup _{j=1}^{i-1}A_{j}\right)\end{array}}$

Wegen $A_{i}\backslash \bigcup _{j=1}^{i-1}A_{j}\subseteq A_{i}$ folgt mit der Monotonie für $i,n\geq 2$

${\begin{aligned}m\left(\bigcup _{i=1}^{n}A_{i}\right)=&m(A_{1})+\sum _{i=2}^{n}m\left(A_{i}\backslash \bigcup _{j=1}^{i-1}A_{j}\right)\leq \sum _{i=1}^{n}m(A_{i})\end{aligned}}$

Ausblick

Sowohl die endliche Differenz von Quaderfiguren als auch ihre endliche Vereinigung sind wiederum Quaderfiguren. In einem späteren Abschnitt werden wir sehen, dass das Mengensystem der Quaderfiguren einen Ring bildet.