Mathematik: Diskrete Mathematik: Mengenlehre
Definition
[Bearbeiten]Eine Menge ist eine Sammlung von verschiedenen Dingen, wie z.B.
- Zahlen
- Buchstaben
- Farbe
- Figuren
- Namen
Mengen werden mit Großbuchstaben benannt.
Darstellungen
[Bearbeiten]Es gibt verschiedene Möglichkeiten eine Menge darzustellen:
- graphisch mit Hilfe von Mengenbildern
- in aufzählender Form:
- in beschreibender Form:
Elemente
[Bearbeiten]Die in der Menge beinhalteten Objekte nennt man Elemente.
(lies "x ist Element von A")
bedeutet, dass x ein Element der Menge A ist, also in dieser Menge liegt.
(lies "x ist nicht Element von A") bedeutet, dass x kein Element der Menge A ist, also nicht in A liegt.
Beispiel:
Besitzt eine Menge keine Elemente, so ist sie die leere Menge.
Eine Menge kann jedoch eine leere Menge enthalten !
Gleichheit
[Bearbeiten]Zwei Mengen sind gleich, wenn sie genau die gleichen Elemente beinhalten. Beim Aufzählen von Mengen zählt weder die Reihenfolge der einzelnen Elemente, noch die Anzahl der gleichen Elemente.
Mächtigkeit
[Bearbeiten]Die Mächtigkeit einer endlichen Menge ist die Anzahl ihrer Elemente.
Beispiele:
Bei unendlichen Mengen hat wird der Anzahlbegriff problematisch; die Mächtigkeit wird durch ein Symbol ausgedrückt, das ausdrücklich keine Zahl im arithmetischen Sinne ist.
Für die Mächtigkeit der natürlichen Zahlen schreibt man
(gesprochen aleph null).
Aus Mengen gebildete Mengen
[Bearbeiten]- Die Teilmenge: Die Teilmenge ist eine Menge die in der Ausgangsmenge enthalten ist, und so alle Elemente dieser beinhaltet.
Datei:Teilmenge.png - Die Potenzmengen: Die Potenzmenge beinhaltet alle möglichen Teilmengen.
Die Mächtigkeit der Potenzmenge beträgt immer die Potenz von 2 mit der Mächtigkeit der Ausgangsmenge:
Datei:Menge aller teilmengen.png
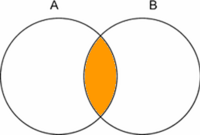
- Die Schnittmenge: Die Schnittmenge beinhaltet alle Elemente, die gleichzeitig in der Menge A und B enthalten ist.
- Die Vereinigungsmenge: Die Vereinigungsmenge beinhaltet alle Elemente, die entweder in A oder in B enthalten sind.
- Die Differenzmenge: Die Differenzmenge beinhaltet alle Elemente, die in A aber nicht in B enthalten sind.
Rechenregeln für Mengenoperationen
[Bearbeiten]Für beliebige Mengen gelten die folgenden Rechenregeln
- Kommutativgesetze
- Assoziativgesetze
- Distributivgesetze
- Absorptionsgesetze
- Idempotenzgesetze
- De Morgansche Regel
Relationen
[Bearbeiten]Definition
[Bearbeiten]Sind die Mengen und endliche, nicht leere Mengen, so heißt (binäre) Relation zwischen A und B.