Dreieckskonstruktionen
Erscheinungsbild
(Weitergeleitet von Mathematikunterricht: Sek: Geometrie: Dreieckkonstruktion)

(Planimetrie/ Dreieckskonstruktionen/ Dreieckskonstruktionen)
Bezeichnungen
[Bearbeiten]- Angaben in kursiver Schrift dienen der Verbesserung der Genauigkeit und sind nicht zwingend notwendig.
Die fünf Standardkonstruktionen
[Bearbeiten]Konstruktion 1 (SSS)
[Bearbeiten]
- Gegeben: Die drei Seiten a, b und c
- Notwendige Bedingung:Die Differenz von zwei Seiten (Betrag) muss kleiner sein als die dritte Seite (Dreiecksungleichungen).
- Trage auf einer Geraden eine der Seiten ab. Am besten die längste Seite.
- Zeichne um einen Endpunkt einen Bogen mit dem Radius, welcher einer anderen Seite entspricht.
- Zeichne um den anderen Endpunkt einen Bogen mit dem Radius, welcher der dritten Seite entspricht.
- Die beiden Schnittpunkte zeigen den dritten Eckpunkt für die beiden spiegelsymmetrischen Lösungen auf.
| Hinweis |
| Sofern auf der Zeichenfläche keine der Seiten eine gegebene Position hat, sollte mit der längsten Seite begonnen werden. Dies ermöglicht das genaueste Ergebnis. |
Konstruktion 2 (SWS)
[Bearbeiten]
- Gegeben: Zwei Seiten und der eingeschlossene Winkel.
- Beispiel
- Gegeben: a, b, γ
- Zeichne die Strecke AC = b
- Trage am Endpunkt C den Winkel γ an.
- Trage auf dem freien Schenkel (Gerade g) die Strecke a ab. Man erhält den dritten Eckpunkt B.
- Verbinde die Punkte A und B miteinander.
Konstruktion 3 (WSW)
[Bearbeiten]
Gegeben: Eine Seite und die anliegenden Winkel.
- Beispiel
- Gegeben: c, α und β
- Trage auf einer Geraden die Seite c ab.
- Trage an die Enden der Seite c auf einer Seite der Geraden die Winkel β und α an.
- Verlängere ggf. die freien Schenkel (f und g) der Winkel bis sie sich (im Punkt C) schneiden.
- Notwendige Bedingung: Die Summe der beiden Winkel ist kleiner als der gestreckte Winkel.
Konstruktion 4 (SWW)
[Bearbeiten]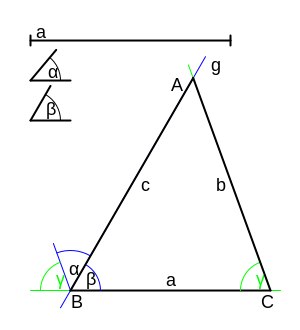
Gegeben: Eine Seite, ein anliegender und der gegenüberliegende Winkel.
- Beispiel
- gegeben: a, β und α.
- Trage auf einer Geraden die Seite a ab.
- Trage an einem Ende der Seite a (Ecke B) den Winkel β an (Gerade g).
- Trage in Punkt B an den freien Schenkel den Winkel α nach außen an. Man erhält den Winkel α + β
- Der Winkel zwischen dem so gewonnenen weiteren freien Schenkel und der Gerade, auf der sich die Seite a befindet, ist der Winkel 180° - α - β = γ.
- Trage den Winkel γ an der Ecke C an.
- Verlängere ggf. die freien Schenkel der Winkel β und γ bis sie sich (im Punkt A) schneiden.
1. Alternativ ab 4.: Verschiebe die sich durch den Winkel α ergebende Strecke von Punkt B parallel nach Punkt C. Der sich ergebende Schnittpunkt dieser Parallelen mit der Geraden g (siehe 2.) ergibt Punkt A.
2. Alternative: Über die Winkelsumme im Dreieck von 180° kann man den dritten Winkel γ = 180° - α vorab berechnen. Dann kann man das Dreieck auch nach Konstruktion 3 (WSW) konstruieren.
Konstruktion 5 (SSW)
[Bearbeiten]Gegeben: Zwei Seiten und ein anliegender Winkel.
- Beispiel
- gegeben: a, b und β.
- Trage auf einer Geraden diejenige Seite ab, an der der gegebene Winkel anliegt, im Beispiel also die Seite a.
- Trage an der Ecke B der Seite a den Winkel β an und verlängere den freien Schenkel.
- Zeichne um den anderen Endpunkt der Seite a, also um die Ecke C, einen Bogen mit dem Radius der Seite b.
- Der Schnittpunkt des Kreisbogens mit dem freien Schenkel von β liefert den dritten Eckpunkt A.
- Hinweis
- Je nachdem, wie lang die beiden Seiten sind und wie groß der Winkel ist (spitz oder stumpf), gibt es keine, eine oder zwei Lösungen. Um eine eindeutige Lösung zu bekommen, muss der Winkel der größeren Seite gegenüber liegen.
Weitere Konstruktionen
[Bearbeiten]Konstruktion 6 (HHH)
[Bearbeiten]Gegeben: Die drei Höhen ha, hb und hc
Diese Konstruktion ist relativ umfangreich und daher auf einer eigenen Seite dargestellt. Siehe dazu unter Dreieck aus drei Höhen.

