Mathematische Übungsbeispiele: Dreiecke und Vierecke
hoch zum Inhaltsverzeichnis
Wenn du nicht weisst, wie du ein Problem lösen kannst, dann gibt es ein leichteres Problem, das du nicht lösen kannst. Finde es!
Flächen von Dreieck und Viereck
[Bearbeiten]Rechtecksfläche
[Bearbeiten]Berechne die Fläche eines Rechtecks mit den Seiten und
Fläche eines rechtwinkligen Dreiecks
[Bearbeiten]Berechne die Fläche eines rechtwinkligen Dreiecks mit den Katheten und
Fläche eines allgemeinen Dreiecks
[Bearbeiten]Berechne die Fläche eines Dreiecks mit und der Höhe über der Seite .
Achtstern
[Bearbeiten]Zwei gleich große Quadrate mit Seitenlänge 1 liegen in Form eines achtzackigen Sterns übereinander. Die jeweiligen Mittelpunkte liegen übereinander, das zweite Quadrat liegt um 45° verdreht zum ersten. Berechne die Fläche der vier überstehenden Ecken des zweiten Quadrats.
Ich habe an dieser Aufgabe in der fünften Gym einen ganzen Nachmittag herumgerechnet. Mit dem richtigen Ansatz geht es aber in fünf Minuten.
Rechteck geschält
[Bearbeiten]Von einem Rechteck mit den Seitenlängen und soll ringsherum ein Streifen einheitlicher Dicke weggeschnitten werden, sodass es auf ein kleineres Rechteck mit der Hälfte der Fläche schrumpft. Gib die Dicke der Schale für die Rechtecke und an.
Archimedes und Wurzel von x
[Bearbeiten]Archimedes überlegt sich, wie er den Umfang eines Kreises mit Radius 1 (und damit die Kreiszahl ) durch eingeschriebene Vielecke näherungsweise berechnen kann. Zuerst berechnet Archimedes den Umfang eines eingeschriebenen Quadrates . Geteilt durch 2 hat das auf dem Taschenrechner den Wert , eine erste Näherung für . Für die nächste Näherung soll jede Seite in der Mitte geteilt werden und aus dem eingeschriebenen Viereck wird ein eingeschriebenes Achteck. Sein halber Umfang ist schon eine bessere Näherung für . Mit der gleichen Berechnungsmethode kannst du auf ein 16-, 32- und 64-Eck verfeinern, prinzipiell immer weiter. Berechne und überprüfe das Ergebnis auf jeweils 4 Stellen hinter dem Komma.
Würfelverdopplung
[Bearbeiten]Das Orakel von Delphi verlangte, dass der würfelförmige Altartisch vergrößert wird, sodass sich sein Volumen verdoppelt. Um welchen Faktor muss die Seitenlänge größer werden?
Rechtecksfläche Status:G Schulstufe:6 Hinweis: Rechteck
rechtwinkliges Dreieck Status:G Schulstufe:6 Hinweis: Fläche des Rechtecks
allgemeines Dreieck Status:G Schulstufe:6 Hinweis: rechtwinkliges Dreieck
Berechne auf fünf Stellen hinter dem Komma: Lösung Achtstern Status:G Schulstufe:9 Hinweise: Dreiecksfläche,Hypotenuse
Berechne auf drei Stellen hinter dem Komma: Lösung a9b5 Lösung a7b3 Status:G Schulstufe:9
Archimedes: Status:G Schulstufe:9
Würfelverdopplung: Berechne auf vier Stellen hinter dem Komma seitenlänge Status:G Schulstufe:8
Trigonometrie
[Bearbeiten]Drei Seiten
[Bearbeiten]Ein Dreieck hat die Seitenlängen , und . Berechne den der Seite c gegenüberliegenden Winkel .
Die Formel, mit der man diese Aufgabe löst, ist eine Verallgemeinerung des Pythagoräischen Lehrsatzes.
Zwei Seiten und der eingeschlossene Winkel
[Bearbeiten]Ein Dreieck schließt mit den Seiten und den Winkel ein. Berechne daraus die Länge der Seite (gegenüberliegend zu ).
Mit dem Spiegel zur Spitze
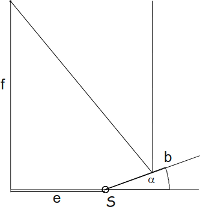
[Bearbeiten]Auf einem zehn Meter langen, senkrecht aufgestellten Stab ist eine Perle befestigt . Fünf Meter vom Fuß des Stabes entfernt ist ein Spiegel drehbar gelagert (Punkt ), die Drehachse steht normal zum Stab . Angenommen die Sonne steht im Zenith (ihre Strahlen fallen senkrecht ein), um welchen Winkel (zum Boden) muss der Spiegel mit Länge gekippt werden, damit der Sonnenstrahl, der von der Spiegelmitte reflektiert wird, die Perle trifft?
Drei Seiten: in Grad und auf drei Stellen hinter dem Komma, Status:G Schulstufe:9 Hinweis: Cosinussatz
Zwei Seiten und der eingeschlossene Winkel: in Grad und auf drei Stellen hinter dem Komma, Status:G Schulstufe:9 Hinweis: Cosinussatz
Mit dem Spiegel zur Spitze: in Grad und auf fünf Stellen nach dem Komma, Status:G Schulstufe:10 Hinweis: Tangens, Arcustangens