Mathematrix: Aufgabenbeispiele/ Direkte und indirekte Beweise

Vollständige Induktion

Quadratensummenformel

Wir zeigen erst einmal, dass, wenn diese Formel für eine zufällige natürliche Zahl m gilt, dann wird sie auch für m+1 gelten (also für die nächste natürliche Zahl). Wir nehmen also an, dass ${\sum }_{k=1}^m{k}^2=\frac{m\cdot (m+1)\cdot (2m+1)}{6}$ schon gilt. Wenn wir m durch m+1 ersetzen, bekommen wir die Formel:

$\sum _{k=1}^{m+1}{k}^2=\frac{(m+1)\cdot (m+2)\cdot (2m+3)}{6}$

Wird diese Formel auch gelten?

$\sum _{k=1}^m{k}^2=\frac{m\cdot (m+1)\cdot (2m+1)}{6}$ (nächster Schritt: auf beide Seiten (m+1)² addieren)

$\sum _{k=1}^m{k}^2+(m+1{)}^2=\frac{m\cdot (m+1)\cdot (2m+1)}{6}+(m+1{)}^2$ (nächster Schritt: rechts gemeinsamen Nenner erzeugen)

$\sum _{k=1}^{m+1}{k}^2=\frac{m\cdot (m+1)\cdot (2m+1)}{6}+\frac{6\cdot (m+1{)}^2}{6}$ (nächster Schritt: Brüche mit gemeinsamer Nenner als ein Bruch schreiben)

$\sum _{k=1}^{m+1}{k}^2=\frac{m\cdot (m+1)\cdot (2m+1)+6\cdot (m+1{)}^2}{6}$ (nächster Schritt: (m+1) Herausheben)

$\sum _{k=1}^{m+1}{k}^2=\frac{(m+1)\cdot (m(2m+1)+6(m+1))}{2}$ (nächster Schritt: manche Rechnungen im Zähler durchführen)

$\sum _{k=1}^{m+1}{k}^2=\frac{(m+1)\cdot (2m^2+7m+6}{6}$

$\sum _{k=1}^{m+1}{k}^2=\frac{(m+1)\cdot (m+2)\cdot (2m+3)}{6}$

Wir haben also gezeigt, dass, wenn die Formel für irgendeine natürliche Zahl gilt, dann wird sie sicherlich auch für die nächste gelten. Zeigen wir jetzt, dass diese Formel für m=1 gilt:

$\sum _{k=1}^1{k}^2=\frac{1\cdot (1+1)\cdot (2\cdot 1+1)}{6}$

$1=\frac{1\cdot 2\cdot 3}{6}$

...was selbstverständlich gilt. Daher gilt der Satz für alle natürliche Zahlen.

Summenformel ungerader Quadrate

Wir zeigen erst einmal, dass, wenn diese Formel für eine zufällige natürliche Zahl m gilt, dann wird sie auch für m+1 gelten (also für die nächste natürliche Zahl). Wir nehmen also an, dass ${\sum }_{k=1}^m(2k-1{)}^2=\frac{m\cdot (2m-1)\cdot (2m+1)}{3}$ schon gilt. Wenn wir m durch m+1 ersetzen, bekommen wir die Formel:

$\sum _{k=1}^{m+1}(2k-1{)}^2=\frac{(m+1)\cdot (2m+1)\cdot (2m+3)}{3}$

Wird diese Formel auch gelten?

$\sum _{k=1}^m(2k-1{)}^2=\frac{m\cdot (2m-1)\cdot (2m+1)}{3}$ (nächster Schritt: auf beide Seiten (m+1)² addieren)

$\sum _{k=1}^m(2k-1{)}^2+(2m+1{)}^2=\frac{m\cdot (2m-1)\cdot (2m+1)}{3}+(2m+1{)}^2$ (nächster Schritt: rechts gemeinsamen Nenner erzeugen)

$\sum _{k=1}^{m+1}(2k-1{)}^2=\frac{m\cdot (2m-1)\cdot (2m+1)}{3}+\frac{3\cdot (2m+1{)}^2}{3}$ (nächster Schritt: Brüche mit gemeinsamer Nenner als ein Bruch schreiben)

$\sum _{k=1}^{m+1}(2k-1{)}^2=\frac{m\cdot (2m-1)\cdot (2m+1)+3\cdot (2m+1{)}^2}{3}$ (nächster Schritt: (2m+1) Herausheben)

$\sum _{k=1}^{m+1}(2k-1{)}^2=\frac{(2m+1)\cdot (m(2m-1)+3(2m+1))}{3}$ (nächster Schritt: manche Rechnungen im Zähler durchführen)

$\sum _{k=1}^{m+1}(2k-1{)}^2=\frac{(2m+1)\cdot (2m^2+5m+3}{3}$

$\sum _{k=1}^{m+1}(2k-1{)}^2=\frac{(2m+1)\cdot (m+1)\cdot (2m+3)}{3}$

Wir haben also gezeigt, dass, wenn die Formel für irgendeine natürliche Zahl gilt, dann wird sie sicherlich auch für die nächste gelten. Zeigen wir jetzt, dass diese Formel für m=1 gilt:

$\sum _{k=1}^1(2k-1{)}^2=\frac{1\cdot (2\cdot 1-1)\cdot (2\cdot 1+1)}{3}$

$1=\frac{1\cdot 1\cdot 3}{3}$

...was selbstverständlich gilt. Daher gilt der Satz für alle natürliche Zahlen.

Geometrische Beweise

Gleichseitiges Dreieck

Wir wenden den Satz des Pythagoras für die Hälfte des Dreiecks an:

${\left(\frac{a}{2}\right)}^2+h^2=a^2\Rightarrow h^2=a^2-{\left(\frac{a}{2}\right)}^2\Rightarrow h=\sqrt{\frac{4a^2-a^2}{4}}=\sqrt{\frac{3a^2}{4}}\Rightarrow h=\frac{\sqrt{3}a}{2}$

Die Formel für ein rechtwinkeliges Dreieck mit Katheten a und b ist $A=\frac{a\cdot b}{2}.$ Wir haben zwei rechtwinkeligen Dreiecke (linker und rechter Teil des gleichseitigen Dreiecks) mit Seiten $h=\frac{\sqrt{3}a}{2}$ und $b=\frac{a}{2}.$ Daher ist die Fläche:

$A=2\frac{a\cdot b}{2}=h\cdot \frac{a}{2}=\frac{\sqrt{3}a}{2}\cdot \frac{a}{2}\Rightarrow$

$A=\frac{\sqrt{3}}{4}{a}^2$

Goldener Schnitt

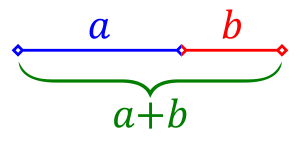
Laut Definition sollte gelten:

$\frac{a}{b}=\frac{a+b}{a}\Rightarrow a^2=a\cdot b+b^2\Rightarrow a^2-b\cdot a-b^2=0$

Laut Formel für die quadratische Gleichung gilt für ihre Lösungen (wenn a die unbekannte Variable ist):

$a_{1,2}=\frac{b}{2}\pm \frac{\sqrt{b^2+4\cdot b^2}}{2}\Rightarrow a_{1,2}=\frac{b}{2}\pm \frac{b\cdot \sqrt{5}}{2}\Rightarrow$ (Wir nehmen nur die positive Lösung)

$\frac{a}{b}=\frac{a+b}{a}=\frac{\sqrt{5}+1}{2}(=\frac{2}{\sqrt{5}-1})$

Quadratfläche mit Diagonale

Laut Formel für die Diagonale d bei einem Quadrat mit Seite a gilt:

$d=\sqrt{2}\cdot a\Rightarrow a=\frac{d}{\sqrt{2}}$

Laut Formel für die Fläche:

$A=a^2={\left(\frac{d}{\sqrt{2}}\right)}^2\Rightarrow$

$A=\frac{d^2}{2}$

Widerspruchsbeweise

Minus Punkt Minus

$a\ne 0$

$-1\cdot (a-a)=-1\cdot 0=0$

Falls Minus mal Minus gleich Minus: $-1\cdot (a-a)=-a-a=-2a\ne 0$ Widerspruch!

Falls Minus mal Minus gleich Plus: $-1\cdot (a-a)=-a+a=0$ Wahre Aussage!

Wurzel 3 Irrationalität

Erst zeigen wir, dass das Quadrat von Zahlen, die durch 3 teilbar sind immer auch Zahlen sind, die auch durch 3 teilbar sind. Wir zeigen auch, dass das Quadrat von Zahlen, die nicht durch 3 teilbar sind immer auch Zahlen sind, die auch nicht durch 3 teilbar sind:

Sei m eine Zahl, die durch 3 teilbar ist. Nennen wir das Ergebnis der Teilung k. Dann gilt:

$m=3\cdot k$

$m^2=(3\cdot k{)}^2$

$m^2=3\cdot (3\cdot k^2)$

Also: das Quadrat einer Zahl, die durch 3 teilbar ist, ist auch eine Zahl, die durch 3 teilbar ist.

Sei n eine Zahl, die nicht durch 3 teilbar ist. Diese Zahl kann zwei Formen haben: $n=3\cdot k+1$ oder $n=3\cdot k+2.$ Für den ersten Fall gilt:

$m=3\cdot k+1$

$m^2=(3\cdot k+1{)}^2$

$m^2=9k^2+6\cdot k+1$

$m^2=3(3k^2+2\cdot k)+1$

Also: das Quadrat ist auch nicht durch 3 teilbar.

Für den zweiten Fall gilt:

$m=3\cdot k+2$

$m^2=(3\cdot k+2{)}^2$

$m^2=9k^2+12\cdot k+4$

$m^2=3(3k^2+4\cdot k+1)+1$

Also: das Quadrat ist auch nicht durch 3 teilbar.

Daraus folgt:

Satz 1: Wenn das Quadrat einer Zahl durch 3 teilbar ist, dann kann diese Zahl nur auch durch 3 teilbar sein,...

...weil, wenn sie nicht durch 3 teilbar wäre, ihr Quadrat doch auch nicht durch 3 teilbar wäre.

Nehmen wir also jetzt an, dass $\sqrt{3}=\frac{a}{b}$, wobei a und b teilerfremd sind. Dann gilt:

$3=\frac{a^2}{b^2}\Rightarrow a^2=3\cdot b^2$

Nach Satz 1 bedeutet dies, dass a eine durch 3 teilbare Zahl ist (da ihr Quadrat auch eine durch 3 teilbare Zahl ist). Schreiben wir also: $a=3\cdot q$, wo $q$ der Quotient von a durch 3 ist. Dann gilt:

$(3\cdot q{)}^2=3\cdot b^2\Rightarrow 9\cdot q^2=3\cdot b^2\Rightarrow 3\cdot q^2=b^2$

was dann nach Satz 1 bedeutet, dass b AUCH eine durch 3 teilbare Zahl ist. Das kann aber nicht sein, weil wir angenommen haben, dass a und b teilerfremd sind, also dass sie keinen gemeinsamen Primfaktor haben.

Wenn wir also vermuten, dass $\sqrt{3}=\frac{a}{b}$, also ein Bruch von natürlichen Zahlen, ist, sollten diese Zahlen gleichzeitig teilerfremd sein UND 3 als gemeinsamen Teiler haben. Dies ist selbstverständlich nicht möglich. Daher kann es nicht sein, dass $\sqrt{3}$ ein Bruch von natürlichen Zahlen, also eine rationale Zahl, ist. Daher ist sie eine irrationale Zahl.