Natur und Technik für den Pflichtschulabschluss: Exkurs: die Kreativität in der Wissenschaft
Das Experiment von Rutherford zeigt uns, wie wichtig die Kreativität in der Wissenschaft ist. Ein einfacheres Beispiel dieser Kreativität ist die Vermessung der Erde von Eratosthenes.
Die Vermessung der Erde nach Eratosthenes
[Bearbeiten]
Eratosthenes war ein griechischer Gelehrter der antiken Zeit mit Beiträgen auf den Gebieten der Mathematik, Astronomie, Geographie, Geschichte, Philosophie, Musik und Dichtung. Er war zuständig für die damalige Bibliothek in Alexandria in Ägypten.
Der Geschichte nach wurde er informiert, dass am Tag der Sommersonnenwende in Syene, eine Stadt in Ägypten, die Sonne mittags keinen Schatten wirft. In Alexandria hingegen, wo er gewohnt hat, bildeten die Sonnenstrahlen einen Winkel von 1/50 des Kreises (also 7° 12') zur Schwerlinie (also zur Senkrechten auf die Erdoberfläche). Er nahm an, dass Alexandria und Syene auf dem gleichen Meridian liegen (was nicht genau, aber auch nicht so ungenau ist).
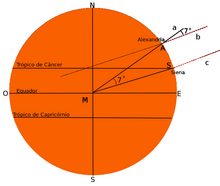
Das realitätsnahe Bild links hilft uns den Sachverhalt zu verstehen, die Skizze rechts zeigt uns, wie Eratosthenes seine Messungen durchgeführt hat.

Die Sonnenstrahlen sind in der Skizze links durch die Geraden b und c dargestellt, die Senkrechte auf der Erdoberfläche in Alexandria durch die Gerade a. Geraden a und b schneiden einander am Punkt A, dort, wo Alexandria ist, Geraden a und c am Punkt M, also am Mittelpunkt des Kreises. Da b und c parallel sind, ist der Winkel zwischen a und b am Punkt A gleich so groß wie der Zentriwinkel zwischen a und c am Punkt M. Den Abstand auf der Erdoberfläche zwischen A und S (also zwischen Alexandria und Syene) kann man messen (835 km). Vermutlich hat Eratosthenes diese Strecke durch königliche Schrittzähler genau ausmessen lassen. Diese Strecke verhält sich zum Erdumfang genau so, wie der Zentriwinkel (7° 12') zum ganzen Kreis (360°). Daher kann man mit Hilfe der Schlussrechnung ganz einfach den Erdumfang und den Erdradius messen.
| U (Erdumfang) | entspricht … | 360° |
| AS (835 km) | entspricht … | 7,2° |
Der tatsächliche Wert liegt nach heutigen Messungen bei ca. 40030 km. Eratosthenes hat für den Abstand AS die in der Antike gebräuchliche Einheit "Stadium" benutzt. Da wir heute nicht genau wissen, wie viel Meter ein Stadium war, können wir nicht genau sagen, wie genau oder ungenau seine Messungen waren. Anscheinend aber war der Fehler in der Messung weniger als 5%!


