Spieleprogrammierung mit Delphi und GLScene: Bewegungen
Bewegungen
[Bearbeiten]Grundsätzlich gibt es drei Typen von Bewegungen:
- Transformation. Das Objekt wird entlang einer oder mehrerer der drei Achsen X, Y und Z bewegt.
- Rotation. Das Objekt wird um eine oder mehrere der drei Achsen gedreht.
- Skalierung. Das Objekt wird in seiner Größe verändert.
Mehr dazu in den drei Unterkapiteln.
Transformation
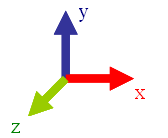
[Bearbeiten]Dazu müssen wir erst einmal wissen, wie das GLScene-Koordinatensystem aussieht, das identisch mit dem OpenGL-Koordinatensystem ist:
Nun hat jedes Objekt, zum Beispiel ein GLCube, eine Eigenschaft Position:
- Position.X - die Position auf der X-Achse
- Position.Y - die Position auf der Y-Achse
- Position.Z - die Position auf der Z-Achse
Dabei handelt es sich um Single-Werte! Aus der Abbildung geht hervor:
- Die X-Achse wächst nach rechts. Positive Werte liegen also rechts vom Koordinatenursprung, negative Werte links.
- Die Y-Achse wächst nach oben. Je größer der Y-Wert, desto höher liegt das Objekt.
- Die Z-Achse wächst zum Betrachter hin. Je größer der Z-Wert, desto näher ist Sie am Betrachter.
Durch verändern der X, Y und Z Werte wird ein Objekt verschoben.
Rotation
[Bearbeiten]Man kann nun ein Objekt um jede Achse drehen. Jedes Objekt hat folgende Eigenschaften:
- PitchAngle - Rotation um die X-Achse
- TurnAngle - Rotation um die Y-Achse
- RollAngle - Rotation um die Z-Achse
Dabei werden Angaben im Gradmaß (nicht wie vielleicht erwartet im Bogenmaß) verlangt! Vorsicht ist geboten, denn die sin()- und cos()-Funktionen erwarten Angaben im Bogenmaß. Hier muss man gegebenenfalls umrechnen. Im Prinzip Dreisatz. Allerdings teilen wir nicht durch (360 / (2 * Pi)) sondern gleich durch 57.29 und holen so bessere Rechenzeiten heraus. Ein Beispiel dafür:
GLDummyCube1.X := GLDummyCube1.X -
sin(GLDummyCube1.TurnAngle / 57.29) * _speed;
GLDummyCube1.Z := GLDummyCube1.Z -
cos(GLDummyCube1.TurnAngle / 57.29) * _speed;
Gegebenenfalls sollte man sich noch einmal ansehen, was Sinus und Cosinus bedeuten, zum Beispiel in der Wikipedia.
Skalierung
[Bearbeiten]Dafür gibt es die Eigenschaften Scale.X, Scale.Y und Scale.Z. Zu beachten ist, dass Position-Werte immer den Mittelpunkt des Objektes beschreiben!
<< Materials | Inhalt | 3D-Modelle laden >>