Statistik: Normalverteilung

Was ist die Normalverteilung?

Normalverteilung des Gewichts von Eiern (g)

Beispiel:

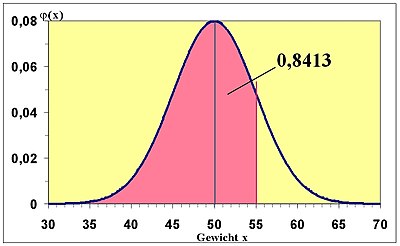
Auf einer Hühnerfarm mit sehr vielen Hühnern werden eine Woche lang die einzelnen Eier gewogen. Definieren wir die Zufallsvariable X: Gewicht eines Eies in Gramm. Es stellt sich heraus, dass ein Ei im Durchschnitt 50 g wiegt. Der Erwartungswert $EX$ ist daher 50. Außerdem sei bekannt, dass die Varianz varX = 25 g² beträgt. Man kann die Verteilung des Gewichts annähernd wie in der Grafik darstellen. Man sieht, dass sich die meisten Eier in der Nähe des Erwartungswerts 50 befinden und dass die Wahrscheinlichkeit, sehr kleine oder sehr große Eier zu erhalten, sehr klein wird. Wir haben hier eine Normalverteilung vor uns. Sie ist typisch für Zufallsvariablen, die sich aus sehr vielen verschiedenen Einflüssen zusammensetzen, die man nicht mehr trennen kann, z.B. Gewicht des Huhns, Alter, Gesundheit, Standort, Vererbung usw.

Die Dichtefunktion der Normalverteilung ist definiert als

$\phi _{x}(x|\mu ;\sigma ^{2})={\frac {1}{\sqrt {2\cdot \pi \cdot \sigma ^{2}}}}\ \exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right){\text{ für x }}\in \mathbb {R} \;,$

wobei $E(X)=\mu$ und $varX=\sigma ^{2}$ ist. Man sagt, X ist normalverteilt mit den Parametern μ und σ², in Symbolschreibweise

$X\sim \phi _{x}(x|\mu ;\sigma ^{2})$ oder kürzer $X\sim N(\mu ;\sigma ^{2})\;.$

In unserem Beispiel ist $X\sim N(50;25)\;.$

Die Normalverteilung ist symmetrisch bezüglich μ. Die Verteilung P(X ≤ a) von X ist wieder die Fläche unter dem Graphen der Dichtefunktion. Sie wird bezeichnet als

$P(X\leq a)=\Phi _{x}(a|\mu ;\sigma ^{2}){\text{ für alle a }}\in \mathbb {R} \;.$

Beispielsweise beträgt die Wahrscheinlichkeit, dass ein Ei höchstens 55 g wiegt, 0,8413. Das entspricht der roten Fläche in der Abbildung.

Das Integral der Dichtefunktion kann nicht analytisch berechnet werden. Die Werte der Verteilungsfunktion liegen i. a. tabellarisch vor. Es besteht nun das Problem, dass für jeden Wert von μ und σ² eine eigene Tabelle vorliegen müsste. Hier ist hilfreich, daß die aus X standardisierte Zufallsvariable Z wiederum normalverteilt ist und zwar mit den Parametern 0 und 1. Es kann jede beliebige Normalverteilung standardisiert werden. Mit Hilfe der standardisierten Zufallsvariablen wird dann die gesuchte Wahrscheinlichkeit bestimmt.

Standardnormalverteilung

Dichtefunktion der Standardnormalverteilung

Man definiert also eine neue Zufallsvariable

$Z={\frac {X-EX}{\sqrt {varX}}}={\frac {X-\mu }{\sigma }}.$

Diese Zufallsvariable Z ist normalverteilt mit EZ = 0 und varZ = 1. Ihre Dichtefunktion ist in der folgenden Grafik dargestellt. Es ist also $Z\sim N(0;1)\;.$

Die Dichtefunktion von Z ist

$\phi _{z}(z|0;1)={\frac {1}{\sqrt {2\cdot \pi }}}\exp \left(-{\frac {z^{2}}{2}}\right){\text{ für z }}\in \mathbb {R}$

Ihre Verteilung, die man auch kurz als Φ(z) bezeichnet, ist (z const.)

$P(Z\leq z)=\Phi (z)=\int _{-\infty }^{z}\phi (u)du.$

Verteilungswerte

Es ist beispielsweise die Wahrscheinlichkeit

$P(Z\leq 0{,}44)=0{,}6700$

und

$P(Z>1{,}64)=0{,}0505.$

Wir wollen nun den Anteil der Eier mit höchstens 55 g bestimmen, also P(X ≤ 55). Wir standardisieren:

$z={\frac {x-\mu }{\sigma }}={\frac {55-50}{\sqrt {25}}}=1\;.$

Es ist dann

$P(X\leq 55)=P(Z\leq 1)=\Phi (1)=0{,}8413.$

Der Wert 0,8413 der Verteilungsfunktion wird in der Normalverteilungstabelle ermittelt. Der folgende Ausschnitt aus der Tabelle soll die Vorgehensweise verdeutlichen: In der ersten Spalte der Tabelle sind die zwei ersten signifikanten Stellen der Ausprägung z angegeben, in der ersten Tabellenzeile die zweite Nachkommastelle, so dass sich beispielsweise z = 1,00 zusammensetzt aus 1,0 + 0,00. Wo sich Zeile und Spalte des betreffenden Z-Wertes kreuzen, steht die gesuchte Wahrscheinlichkeit.

z	0,00	0,01	0,02
0,0	5000	5040	5080
0,1	5398	5438	5478
0,2	5793	5832	5871
0,3	6179	6217	6255
0,4	6554	6591	6628
0,5	6915	6950	6985
0,6	7257	7291	7324
0,7	7580	7611	7642
0,8	7881	7910	7939
0,9	8159	8186	8212
1,0	8413	8438	8461
1,1	8643	8665	8686
1,2	8849	8869	8888

Der errechnete Wert z kann gerundet werden, falls die errechneten Stellen die Zahl der Stellen des tabellierten z-Wertes übertreffen. Da die Verteilung von Z symmetrisch bezüglich μ = 0 ist, genügt die Tabellierung der Verteilungswerte ab z = 0 bzw. Φ(z) = 0,5. Es gilt, wie man auch anhand der Grafik leicht sieht:

$P(Z\leq -z)=P(Z\geq z)=1-P(Z\leq z)=1-\Phi (z)$

bzw.

$\Phi (-z)=1-\Phi (z)$ .

Beispiel:

${\begin{matrix}P(Z\leq -1)&=&P(Z\geq 1)&=&1-P(Z\leq 1)&\\&=&1-\Phi (1)&=&1-0{,}8413&=0{,}1587\end{matrix}}$

Quantil

Häufig sucht man zu einer gegebenen Wahrscheinlichkeit p den dazugehörigen z-Wert z(p). Er wird als p-Quantil bezeichnet.

Es gilt also:

$P(Z\leq z(p))=p$ .

97,5%-Quantil der Standardnormalverteilung

Beispielsweise ist z(0,975) = 1,96. Es ist also hier die Wahrscheinlichkeit 0,975 gegeben und der dazugehörige z-Wert wird gesucht. Man sucht in der Tabelle die Wahrscheinlichkeit 0,9750 und bestimmt dann am Rand den betreffenden z-Wert 1,96.

Liegt p zwischen zwei Tabellenwerten, genügt es, als p den Tabellenwert zu verwenden, der p am nächsten liegt.

Beispiel:

Gesucht: z(0,9)

	näher bei	0,9
Wahrscheinlichkeit Φ	0,8997		0,9015
z-Wert oder Quantil	1,28		1,29

Es ist also z(0,9) ≈ 1,28.

Für eine Normalverteilung mit μ und σ² berechnet sich das p-Quantil als

$x(p)=\mu +\sigma \cdot z(p).$

Beispiel:

Wie schwer sind höchstens die 2/3 leichtesten Eier? Gesucht ist also x(0,67):

$x(p)=50+5\cdot z(0,67)=50+5\cdot 0{,}44=52{,}2.$

Das schwerste der 67% leichtesten Eier wog also 52,2g .

Übung zur Berechnung von Φ_Z(z)

Schraffieren Sie die gesuchte Wahrscheinlichkeit in der Grafik und berechnen Sie die gesuchten Werte:

P(Z ≤ 0,51)	P(Z ≤ 2,0) =	P(Z ≤ - 0,51)
P(1,5 ≤ Z ≤ 2,35)	P(- 0,8 ≤ Z ≤ 1,05)	P(Z ≥ -0,89)
P( Z ≤ -1,68 ∪ Z ≥ 2 )	P(Z ≤ -1,96 ∪ Z ≥ 1,96)	P(Z ≤ -5)
z(0,975)	z(0,8)	z(0,2)

Übungen zum Eier-Beispiel

1. Wie groß ist die Wahrscheinlichkeit, daß ein Ei höchstens 60 g wiegt?
2. Wieviel Prozent der Eier wiegen höchstens 50 g?
3. Wie groß ist die Wahrscheinlichkeit, daß ein Ei mindestens 45 g wiegt?
4. Wieviel Prozent der Eier liegen zwischen 45 und 55 Gramm?
5. Mit welcher Wahrscheinlichkeit wiegt ein Ei genau 53 Gramm?
6. Welches Mindestgewicht haben die 30% schwersten Eier?

Lösungen:

Übung zur Berechnung von Φ_z(z)

a) 0,6950 b) 0,9772 c) 0,3050 d) 0,0574 e) 0,6412 f) 0,8133 g) 0,0693 h) 0,05 i) 0 j) 1,96 k) 0,84 l) -0,84

Weblink

Durchschnittsgewicht von Eiern

↓  Zentraler Grenzwertsatz

↑  Stetige Verteilungen

↑↑ Inhaltsverzeichnis Statistik