- Das Seil (die Kette) kann keine Momente oder Querkräfte übertragen (biegeschlaffes Seil, biegeschlaffe Kette).
- Die Seillänge (Kettenlänge) wird als konstant angenommen (dehnstarres Seil, dehnstarre Kette).
- Als Schnittkräfte treten nur Zugkräfte auf.
Die Kettenlinie (oder Katenoide) ist die geometrische Form, welche eine an ihren beiden Enden abgehängte Kette oder ein entsprechendes Seil unter der Belastung durch ihr Eigengewicht ausbildet. Das Eigengewicht sei dabei gleichmäßig über die Gesamtlänge der Kette (des Seiles) verteilt.



 |
 |
 |
(Gl.1)
|
 |
 |
 |
(Gl.2)
|
 |
 |
 |
(Gl.3)
|
Die Differentialgleichung der Kettenlinie
[Bearbeiten]


aus (Gl.2) 

aus (Gl.3) 

mit  (Seilparameter) folgt
(Seilparameter) folgt
 (Gl.4) (Gl.4)
|
(Gl.4):


Lösung dieser DGL mittels Separation der Variablen:

Substitution:







Randbedingung:
Die Position des Koordinatensystems kann frei gewählt werden. Zwecks Vereinfachung wird hier das Koordinatensystem so positioniert, dass die horizontale Tangente an die Kettenlinie genau bei der Koordinate (0, a) anliegt.

Es gilt somit  für
für 

 (Gl.5) (Gl.5)
|


Randbedingung:  für
für 

 (Gl.6) (Gl.6)
|

Die Bogenlänge:




Randbedingung:  für
für 
 (Gl.7) (Gl.7)
|
Weiters gilt:

 (Gl.8) (Gl.8)
|
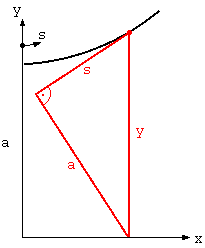
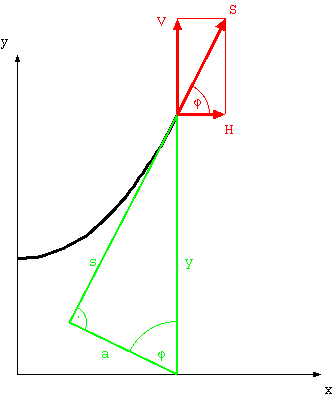
aus (Gl.2): 

Randbedingung: für  ist
ist 
 (Gl.9) (Gl.9)
|

 (Gl.10) (Gl.10)
|

 (Gl.11) (Gl.11)
|
Die Traktrix (Schleppkurve, Hundekurve) ist die Evolvente der Kettenlinie und die Kettenlinie ist die Evolute der Traktrix.
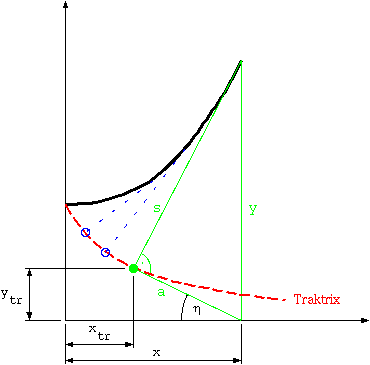





Randbedingung: für  ist
ist 
 (Gl.12) (Gl.12)
|
Eigentlich sind schon fast alle Formeln für die Kettenlinie bekannt. Ein kleines Problem gibt es noch: Wie soll der Wert für den Seilparameter  ermittelt werden?
ermittelt werden?
Die Lösung für a muss mittels zusätzlicher Daten gefunden werden. Nachfolgend wird eine Lösung für die Vorgabe von Seillänge L und den Abständen der Aufhängepunkte, nämlich b und h gezeigt (Ketten- bzw. Seildreieck).
Gegeben sind L, b, h. Gesucht ist der Seilparameter a.
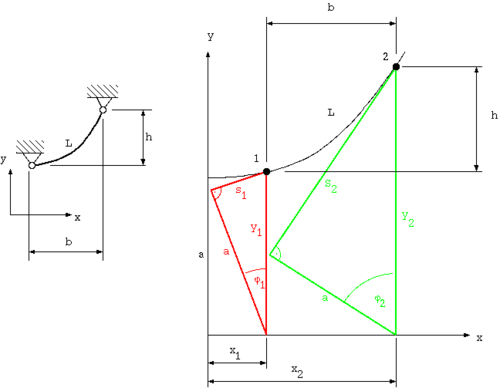





Mit Anwendung der Summationsformel  folgt
folgt

Weitere Vereinfachung durch  und
und 



 (Gl.13) (Gl.13)
|
oder auch in dieser Form
 (Gl.14) (Gl.14)
|
Lösung dieser transzendenten Gleichung:


Die Bestimmung von  und somit von a kann
und somit von a kann
- grafisch
- per Nullstellenberechnung (Newtonsches Näherungsverfahren, o.ä.)
- oder per Näherung durch Reihenentwicklung

erfolgen.
Somit sind alle relevanten Daten für die Kettenlinie aus den bisher hergeleiteten Formeln berechenbar. Sorge bereitet noch, dass die genaue Lage des gegebenen Kettendreiecks auf dieser Kettenlinie nicht bestimmt ist. Relativ einfach lassen sich die Bogenlängen s1 und s2 aus den Geometriebeziehungen (siehe Abb. am Anfang dieses Kettendreieck-Abschnittes) ermitteln.


Nach einigen Umformungsschritten resultiert daraus die quadratische Gleichung


 (Gl.15) (Gl.15)
|
 (Gl.16) (Gl.16)
|
Mit (Gl.13) und der mathematischen Beziehung  wird daraus
wird daraus
 (Gl.17) (Gl.17)
|
 (Gl.18) (Gl.18)
|






 (Gl.19) (Gl.19)
|
Auf ein Tragseil wirkt eine vertikale Streckenlast q(x) ein.

Statisches Gleichgewicht:




Differentialgleichung der Seillinie:
 (Gl.20) (Gl.20)
|
- Gross, Hauger, Schnell, Wriggers: Technische Mechanik 4, Elemente der Höheren Mechanik, Numerische Methoden, 3.Aufl., Springer-Verlag, Berlin-Heidelberg-New York, 1999, ISBN 3-540-65205-1
- Grote, Feldhusen (Hrsg.): Dubbel Taschenbuch für den Maschinenbau, 21. Aufl., Springer-Verlag, Berlin, 2005, ISBN 3-540-22142-5
- Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik, 6. Aufl., Verlag Harri Deutsch, Frankfurt am Main, 2005, ISBN 3-8171-2006-0
- Husty, Karger, Sachs, Steinhilper: Kinematik und Robotik, Springer-Verlag, Berlin-Heidelberg-New York, 1997, ISBN 3-540-63181-X













































































































