Zurück zum Inhaltsverzeichnis
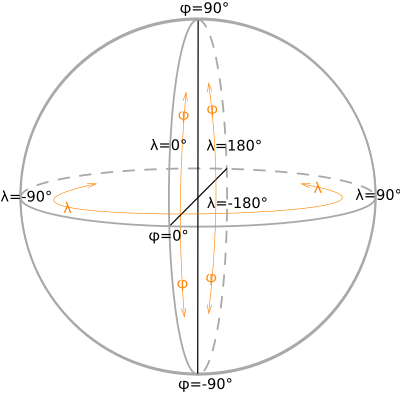
Geodätische Koordinaten auf dem Rotationsellipsoid Das Rotationsellipsoid mit Kreisform der Breitenkreise (in der Äquatorebene Radius der großen Halbachse A) und Ellipsenform bezüglich der Längenkreise. Kleine Halbachse an den Polen ist B.
Die w:Exzentrizität (Mathematik) gibt die Abplattung aufgrund der unterschiedlichen Länge von A und B an.
(
X
Y
Z
)
=
(
N
⋅
cos
U
⋅
cos
V
N
⋅
sin
U
⋅
cos
V
N
⋅
sin
V
(
1
−
E
2
)
)
{\displaystyle {\begin{pmatrix}X\\Y\\Z\end{pmatrix}}={\begin{pmatrix}N\cdot \cos {U}\cdot \cos {V}\\N\cdot \sin {U}\cdot \cos {V}\\N\cdot \sin {V}(1-E^{2})\end{pmatrix}}}
V
∈
(
−
π
2
;
π
2
)
U
∈
[
−
π
;
π
)
{\displaystyle V\in (-{\frac {\pi }{2}};{\frac {\pi }{2}})\,U\in [-\pi ;\pi )}
N
=
A
1
−
E
2
sin
2
V
{\displaystyle N={\frac {A}{\sqrt {1-E^{2}\sin ^{2}V}}}}
A und B bzw. E je nach Ellipsoid.
Siehe Gaußsches Dreibein
g
→
1
=
x
→
U
=
{\displaystyle {\vec {g}}_{1}={\vec {x}}_{U}=}
g
→
2
=
x
→
V
=
{\displaystyle {\vec {g}}_{2}={\vec {x}}_{V}=}
g
→
3
=
x
→
U
(
u
)
×
x
→
V
(
v
)
|
|
x
→
U
(
u
)
×
x
→
V
(
v
)
|
|
=
{\displaystyle {\vec {g}}_{3}={\frac {{\vec {x}}_{U}(u)\times {\vec {x}}_{V}(v)}{||{\vec {x}}_{U}(u)\times {\vec {x}}_{V}(v)||}}=}
Siehe hier :
g
11
=
x
→
U
⋅
x
→
U
=
N
2
cos
2
V
{\displaystyle g_{11}={\vec {x}}_{U}\cdot {\vec {x}}_{U}=N^{2}\cos ^{2}V}
g
12
=
G
21
=
x
→
U
⋅
x
→
V
=
0
{\displaystyle g_{12}=G_{21}={\vec {x}}_{U}\cdot {\vec {x}}_{V}=0}
g
22
=
x
→
V
⋅
x
→
V
=
M
2
{\displaystyle g_{22}={\vec {x}}_{V}\cdot {\vec {x}}_{V}=M^{2}}
G
=
(
g
11
g
12
g
21
g
22
)
=
(
N
2
cos
2
V
0
0
M
2
)
=
(
N
2
cos
2
V
0
0
N
2
(
1
−
E
2
)
2
(
1
−
E
2
sin
2
V
)
2
)
{\displaystyle \mathbf {G} ={\begin{pmatrix}g_{11}&g_{12}\\g_{21}&g_{22}\end{pmatrix}}={\begin{pmatrix}N^{2}\cos ^{2}V&0\\0&M^{2}\end{pmatrix}}={\begin{pmatrix}N^{2}\cos ^{2}V&0\\0&N^{2}{\frac {(1-E^{2})^{2}}{(1-E^{2}\sin ^{2}V)^{2}}}\end{pmatrix}}}
G
−
1
=
(
g
11
g
12
g
21
g
22
)
=
1
1
(
0
0
0
0
)
{\displaystyle \mathbf {G} ^{-1}={\begin{pmatrix}g^{11}&g^{12}\\g^{21}&g^{22}\end{pmatrix}}={\frac {1}{1}}{\begin{pmatrix}0&0\\0&0\end{pmatrix}}}
x
→
u
u
=
{\displaystyle {\vec {x}}_{uu}=}
x
→
u
v
=
{\displaystyle {\vec {x}}_{uv}=}
x
→
v
v
=
{\displaystyle {\vec {x}}_{vv}=}
Hier nachschauen!
b
11
=
x
→
u
u
⋅
n
→
=
{\displaystyle b_{11}={\vec {x}}_{uu}\cdot {\vec {n}}=}
b
12
=
b
21
=
x
→
u
v
⋅
n
→
{\displaystyle b_{12}=b_{21}={\vec {x}}_{uv}\cdot {\vec {n}}}
b
21
=
x
→
v
v
⋅
n
→
=
{\displaystyle b_{21}={\vec {x}}_{vv}\cdot {\vec {n}}=}
B
=
(
b
11
b
12
b
21
b
22
)
=
(
L
M
M
N
)
=
(
0
0
0
0
)
{\displaystyle \mathbf {B} ={\begin{pmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{pmatrix}}={\begin{pmatrix}L&M\\M&N\end{pmatrix}}={\begin{pmatrix}0&0\\0&0\end{pmatrix}}}
Siehe hier . Mit u1 = u, u2 = v.
α
=
1
{\displaystyle \alpha =1}
β
=
1
{\displaystyle \beta =1}
γ
=
1
{\displaystyle \gamma =1}
Γ
11
1
:=
1
2
g
11
(
∂
g
11
∂
u
1
+
∂
g
11
∂
u
1
−
∂
g
11
∂
u
1
)
+
1
2
g
12
(
∂
g
12
∂
u
1
+
∂
g
21
∂
u
1
−
∂
g
11
∂
u
2
)
=
{\displaystyle \Gamma _{11}^{1}:={\frac {1}{2}}g^{11}({\frac {\partial g_{11}}{\partial u^{1}}}+{\frac {\partial g_{11}}{\partial u^{1}}}-{\frac {\partial g_{11}}{\partial u^{1}}})+{\frac {1}{2}}g^{12}({\frac {\partial g_{12}}{\partial u^{1}}}+{\frac {\partial g_{21}}{\partial u^{1}}}-{\frac {\partial g_{11}}{\partial u^{2}}})=}
α
=
2
{\displaystyle \alpha =2}
β
=
1
{\displaystyle \beta =1}
γ
=
1
{\displaystyle \gamma =1}
Γ
12
1
:=
1
2
g
11
(
∂
g
11
∂
u
2
+
∂
g
12
∂
u
1
−
∂
g
21
∂
u
1
)
+
1
2
g
12
(
∂
g
12
∂
u
2
+
∂
g
22
∂
u
1
−
∂
g
21
∂
u
2
)
=
{\displaystyle \Gamma _{12}^{1}:={\frac {1}{2}}g^{11}({\frac {\partial g_{11}}{\partial u^{2}}}+{\frac {\partial g_{12}}{\partial u^{1}}}-{\frac {\partial g_{21}}{\partial u^{1}}})+{\frac {1}{2}}g^{12}({\frac {\partial g_{12}}{\partial u^{2}}}+{\frac {\partial g_{22}}{\partial u^{1}}}-{\frac {\partial g_{21}}{\partial u^{2}}})=}
α
=
1
{\displaystyle \alpha =1}
β
=
2
{\displaystyle \beta =2}
γ
=
1
{\displaystyle \gamma =1}
Γ
11
2
:=
1
2
g
21
(
∂
g
11
∂
u
1
+
∂
g
11
∂
u
1
−
∂
g
11
∂
u
1
)
+
1
2
g
22
(
∂
g
12
∂
u
1
+
∂
g
21
∂
u
1
−
∂
g
11
∂
u
2
)
=
{\displaystyle \Gamma _{11}^{2}:={\frac {1}{2}}g^{21}({\frac {\partial g_{11}}{\partial u^{1}}}+{\frac {\partial g_{11}}{\partial u^{1}}}-{\frac {\partial g_{11}}{\partial u^{1}}})+{\frac {1}{2}}g^{22}({\frac {\partial g_{12}}{\partial u^{1}}}+{\frac {\partial g_{21}}{\partial u^{1}}}-{\frac {\partial g_{11}}{\partial u^{2}}})=}
α
=
1
{\displaystyle \alpha =1}
β
=
1
{\displaystyle \beta =1}
γ
=
2
{\displaystyle \gamma =2}
Γ
21
1
=
Γ
12
1
{\displaystyle \Gamma _{21}^{1}=\Gamma _{12}^{1}}
α
=
2
{\displaystyle \alpha =2}
β
=
1
{\displaystyle \beta =1}
γ
=
2
{\displaystyle \gamma =2}
Γ
12
2
:=
1
2
g
11
(
∂
g
21
∂
u
2
+
∂
g
12
∂
u
2
−
∂
g
22
∂
u
1
)
+
1
2
g
12
(
∂
g
22
∂
u
2
+
∂
g
22
∂
u
2
−
∂
g
22
∂
u
2
)
=
{\displaystyle \Gamma _{12}^{2}:={\frac {1}{2}}g^{11}({\frac {\partial g_{21}}{\partial u^{2}}}+{\frac {\partial g_{12}}{\partial u^{2}}}-{\frac {\partial g_{22}}{\partial u^{1}}})+{\frac {1}{2}}g^{12}({\frac {\partial g_{22}}{\partial u^{2}}}+{\frac {\partial g_{22}}{\partial u^{2}}}-{\frac {\partial g_{22}}{\partial u^{2}}})=}
α
=
1
{\displaystyle \alpha =1}
β
=
2
{\displaystyle \beta =2}
γ
=
2
{\displaystyle \gamma =2}
Γ
21
2
=
Γ
12
2
{\displaystyle \Gamma _{21}^{2}=\Gamma _{12}^{2}}
α
=
2
{\displaystyle \alpha =2}
β
=
2
{\displaystyle \beta =2}
γ
=
2
{\displaystyle \gamma =2}
Γ
22
2
:=
1
2
g
21
(
∂
g
21
∂
u
2
+
∂
g
12
∂
u
2
−
∂
g
22
∂
u
1
)
+
1
2
g
22
(
∂
g
22
∂
u
2
+
∂
g
22
∂
u
2
−
∂
g
22
∂
u
2
)
=
{\displaystyle \Gamma _{22}^{2}:={\frac {1}{2}}g^{21}({\frac {\partial g_{21}}{\partial u^{2}}}+{\frac {\partial g_{12}}{\partial u^{2}}}-{\frac {\partial g_{22}}{\partial u^{1}}})+{\frac {1}{2}}g^{22}({\frac {\partial g_{22}}{\partial u^{2}}}+{\frac {\partial g_{22}}{\partial u^{2}}}-{\frac {\partial g_{22}}{\partial u^{2}}})=}
Zurück zum Inhaltsverzeichnis