Mittelwertsatz – Serlo „Mathe für Nicht-Freaks“
Der Mittelwertsatz ist einer der zentralen Sätze der Differentialrechnung und besagt (grob gesprochen), dass die Steigung der Sekante zwischen zwei verschiedenen Punkten einer differenzierbaren Funktion irgendwo zwischen diesen beiden Punkten als Ableitung angenommen wird. So verknüpft der Mittelwertsatz die Sekantensteigung mit der Ableitung einer Funktion. Globale Eigenschaften, die mit Hilfe der Sekantensteigung ausgedrückt werden können, sind so mit Hilfe des Mittelwertsatzes auf Eigenschaften der Ableitung zurückführbar. Im Abschnitt „Schrankensatz“ werden wir eine nützliche Anwendung untersuchen. Weitere folgen dann in den Kapiteln „Kriterium für Konstanz und Monotoniekriterium“, „Ableitung und lokale Extrema“ und „Regel von L'Hospital“. Auch der Hauptsatz der Differential- und Integralrechnung basiert auf dem Mittelwertsatz.
Motivation
[Bearbeiten]Wir haben uns bereits mit dem Satz von Rolle beschäftigt. Zur Wiederholung: Der Satz von Rolle besagt, dass es für jede stetige Funktion , die in differenzierbar ist und für die gilt, ein Argument geben muss, welches erfüllt:

Wie können wir diesen Satz für den Fall verallgemeinern? Muss die Ableitung für ein auch einen bestimmten Wert annehmen? Zunächst fällt auf, dass nicht zwangsläufig sein muss:

Überlegen wir uns nochmal, wie die Situation beim Satz von Rolle war. Zum einen ist die Steigung der Tangente an den Graphen von in gleich . Zum anderen ist aber auch die Steigung der Sekante durch die beiden Randpunkte und von gleich , da und damit ist. Die Sekante zwischen den Punkten und und die Tangente im Punkt liegen damit parallel:

Sei nun allgemeiner . Betrachten wir die Sekantensteigung zwischen den Punkten und . Diese ist ungleich Null und entspricht der mittleren Steigung von im Intervall . Fassen wir beispielsweise die Funktion als Ortsfunktion eines Autos in Abhängigkeit von der Zeit auf, so entspricht die mittlere Steigung der Durchschnittsgeschwindigkeit des Autos in der Zeit von bis .
Wenn das Auto zum Zeitpunkt schneller als fährt (sprich: Die Ableitung ist größer als die Sekantensteigung ), so muss es bis zum Zeitpunkt Zeiten gegeben haben, an denen es langsamer als gefahren ist, sonst kann es die Durchschnittsgeschwindigkeit nicht erreichen. Bei einem Beschleunigungs- oder Bremsvorgang nimmt das Auto alle Geschwindigkeiten zwischen Anfangs- und Endgeschwindigkeit an und springt nicht einfach von der Anfangs- auf die Endgeschwindigkeit (hier nehmen wir an, dass die Geschwindigkeitsfunktion stetig ist). Da das Auto mal schneller und mal langsamer als war, muss es einen Zeitpunkt geben, an dem es genau die Geschwindigkeit hat. Analog können wir argumentieren, wenn das Auto zum Zeitpunkt langsamer als fährt. Für unsere Funktion bedeutet das, dass es tatsächlich ein geben muss mit . Dies ist die Aussage des Mittelwertsatzes:

Es scheint also ein mit zu geben. Diese Intuition wollen wir im Folgenden zu einem Satz formen und formal korrekt beweisen. In unserer Argumentation haben wir beispielsweise verwendet, dass die Ableitung stetig ist. Nun muss die betrachtete Funktion nicht stetig differenzierbar sein. Dass aber auch in diesem Fall der Mittelwertsatz erfüllt ist, werden wir im Beweis zeigen.
Mittelwertsatz
[Bearbeiten]Der Mittelwertsatz der Differentialrechnung ist eine Verallgemeinerung des Satzes von Rolle und lautet wie folgt:
Satz (Mittelwertsatz)
Sei eine stetige Funktion mit und auf dem offenen Intervall differenzierbar. Dann existiert ein mit .
Hinweis
Die Voraussetzungen, um den Mittelwertsatz anzuwenden, entsprechen denen des Satzes von Rolle, nur dass nicht gelten muss. Die benötigten Prämissen müssen aus denselben Gründen wie beim Satz von Rolle zutreffen. Ebenso liefert der Mittelwertsatz lediglich eine Existenzaussage. Das mit der besagten Eigenschaft existiert, kann in der Praxis aber oftmals nicht explizit bestimmt werden. Auch muss das nicht eindeutig sein. In den folgenden Grafiken ist eine Funktion eingezeichnet, die die Sekantensteigung an zwei Stellen und annimmt:
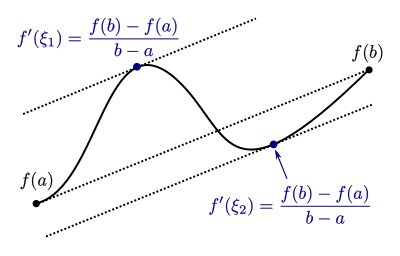
Ein Spezialfall sind lineare Funktionen für mit . In diesem Fall ist für alle . Sprich: die Sekantensteigung wird überall als Tangentensteigung angenommen:

Beweis
[Bearbeiten]Wie kommt man auf den Beweis? (Mittelwertsatz)
Wie oben schon erwähnt, wollen wir den Mittelwertsatz mit Hilfe des Satzes von Rolle beweisen. Dazu müssen wir aus der gegeben Funktion eine Hilfsfunktion so konstruieren, dass wir auf diese den Satz von Rolle anwenden können. Wir benötigen hierzu eine auf stetige und auf differenzierbare Funktion . Zudem sollte sein. Dann gilt mit dem Satz von Rolle für ein . Können wir außerdem die Hilfsfunktion so wählen, dass ist, so folgt aus die Gleichung . Dies ist äquivalent zu , also der Formel des Mittelwertsatzes. Die Funktion
besitzt die gewünschten Eigenschaften. Insbesondere ist
Die folgenden Grafiken illustrieren den Zusammenhang zwischen der Funktion und der Hilfsfunktion :
-
Die Funktion aus dem Mittelwertsatz.
-
Die Hilfsfunktion für den Satz von Rolle.
Beweis (Mittelwertsatz)
Sei eine stetige Funktion mit und auf differenzierbar. Eine passende Hilfsfunktion ist gegeben durch
ist auf stetig und auf differenzierbar, da nach Voraussetzung diese Bedingungen erfüllt und eine Komposition aus und dem Polynom ersten Grades ist. Außerdem gilt
Nach dem Satz von Rolle existiert ein mit . Es wurde also ein gefunden, das erfüllt. Somit folgt die Behauptung des Mittelwertsatzes.
Äquivalenz von Mittelwertsatz und Satz von Rolle
[Bearbeiten]Der Mittelwertsatz und der Satz von Rolle sind sogar äquivalent. Um dies zu zeigen, müssen wir einerseits aus dem Mittelwertsatz den Satz von Rolle folgern und andererseits aus dem Satz von Rolle den Mittelwertsatz beweisen. Letzteres haben wir aber bereits im Beweis dieses Kapitels getan, sodass wir nur noch vom Mittelwertsatz auf den Satz von Rolle schließen müssen.
Sei eine stetige Funktion mit und auf differenzierbar. ist also eine Funktion, auf die der Mittelwertsatz anwendbar ist. Weiterhin gelte , damit auch alle Voraussetzungen des Satzes von Rolle gegeben sind. Nach dem Mittelwertsatz existiert nun ein mit , denn mit ist . Es gibt also tatsächlich ein mit , was genau die Aussage des Satzes von Rolle ist. Damit sind der Mittelwertsatz und der Satz von Rolle äquivalent.
Übungsaufgabe
[Bearbeiten]Aufgabe (Aufgabe)
Sei eine beliebige stetige, in differenzierbare Funktion mit . Welchen Wert muss die Ableitungsfunktion auf jeden Fall annehmen?
Lösung (Aufgabe)
Da alle Prämissen des Mittelwertsatzes gegeben sind, ist dieser hier anwendbar. Deshalb existiert ein mit . Die Ableitungsfunktion muss also auf jeden Fall den Wert annehmen.
Anwendung: Beweis von Ungleichungen
[Bearbeiten]Mit Hilfe des Mittelwertsatzes lassen sich häufig nützliche Ungleichungen beweisen. Der Trick dabei ist, zunächst den Mittelwertsatz auf eine Hilfsfunktion (die oftmals auf einer Seite der Ungleichung steht) anzuwenden. Anschließend schätzen wir dann den Ausdruck passend ab.
Beispielaufgabe: Beweis einer Ungleichung
[Bearbeiten]Aufgabe (Beweis einer Ungleichung mit dem Mittelwertsatz)
Beweise, dass folgende Ungleichung für alle gilt:
Beweis (Beweis einer Ungleichung mit dem Mittelwertsatz)
Wir wählen als Hilfsfunktion
Sei beliebig. Die Funktion ist als Komposition stetiger Funktionen auf stetig und auf differenzierbar. Nach dem Mittelwertsatz gibt es daher ein mit
Nun benutzen wir die Quotientenregel und berechnen Damit können wir wie folgt abschätzen:
Damit gilt die Ungleichung:
Diese Ungleichung ist äquivalent zu der zu beweisenden Behauptung
Ungleichung zum Logarithmus
[Bearbeiten]
Aufgabe (Ungleichung zum Logarithmus)
Zeige mit Hilfe des Mittelwertsatzes, dass folgende Ungleichung für alle erfüllt ist:
Wie kommt man auf den Beweis? (Ungleichung zum Logarithmus)
Für die Ungleichung gilt
Der Ausdruck entspricht dem Differenzenquotienten im Mittelwertsatz angewendet auf die Funktion . Es gibt also ein mit . Wenn wir abschätzen können, so sind wir am Ziel. Nun ist und mit für können wir die Ungleichung beweisen. Schauen wir uns nun die fehlende Ungleichung an:
Wieder erscheint der Differenzenquotient welcher nach dem Mittelwertsatz gleich einer Ableitung für ein ist. Nun ist und damit können wir die fehlende Ungleichung beweisen.
Beweis (Ungleichung zum Logarithmus)
Sei beliebig. Wir definieren durch . Dann ist stetig auf dem kompletten Definitionsbereich und ist auf differenzierbar. Damit ist der Mittelwertsatz anwendbar. Nach diesem existiert ein mit
Beweisschritt:
Wegen ist
Beweisschritt:
Wegen ist
Hinweis
Die Ungleichung lässt sich für alle erweitern. Für gilt
Ist nun , so gibt es ein mit . Damit gilt dann
sowie
Dabei haben wir für die Abschätzungen die beiden oben bewiesenen Ungleichungen verwendet. Also gilt für alle :
Anwendung: Der Schrankensatz
[Bearbeiten]Definition und Beweis des Schrankensatzes
[Bearbeiten]Satz (Schrankensatz)
Sei stetig und in differenzierbar. Weiter sei die Ableitungsfunktion beschränkt. Dann gibt es mit ein , sodass für alle gilt. Insbesondere gilt die Abschätzung, falls auf stetig differenzierbar ist.
Beweis (Schrankensatz)
Seien beliebig gewählt mit . Schränken wir nun den Definitionsbereich von auf ein, so bleiben Stetigkeit und Differenzierbarkeit erhalten. Der Mittelwertsatz ist anwendbar. Also gibt es ein mit .
Da nach Voraussetzung beschränkt ist, existiert . Für dieses gilt für alle . Somit ist . Dies ist äquivalent zur Behauptung.
Wenn stetig differenzierbar auf ist, so besitzt die stetige Ableitungsfunktion ein Maximum und Minimum. Sie ist damit beschränkt und der Satz kann dann auch für diese Funktion angewandt werden.
Lipschitz-Variante des Schrankensatz
[Bearbeiten]
Die Ungleichung für alle besagt, dass Lipschitz-stetig mit Lipschitz-Konstante ist. Daher können wir den Schrankensatz auch folgendermaßen formulieren:
Satz (Lipschitz-Variante des Schrankensatz)
Sei stetig und auf differenzierbar. Weiter sei die Ableitungsfunktion beschränkt. Dann ist Lipschitz-stetig mit Lipschitz-Konstante . Insbesondere ist jede auf stetig differenzierbare Funktion Lipschitz-stetig.
Beispiel (Lipschitz-Stetigkeit von Sinus und Cosinus)
und sind stetig und differenzierbar auf . Außerdem sind deren Ableitungen beschränkt, da für alle gilt:
Damit sind die beiden Funktionen Lipschitz-stetig mit Lipschitz-Konstante . Insbesondere gelten für alle die Abschätzungen
und
Verständnisfrage: Die Umkehrung des Schrankensatzes lautet: „Sei stetig und in differenzierbar. Weiter sei Lipschitz-stetig. Dann ist die Ableitungsfunktion beschränkt.“ Ist diese Aussage richtig?
Ja, diese Aussage stimmt ebenfalls. Da differenzierbar ist existiert für jedes der Grenzwert
Da Lipschitz-stetig ist, gibt es für alle ein mit
Mit der Stetigkeit der Betragfunktion und den Grenzwertsätzen gilt damit
Also ist beschränkt.
Praxis: Geschwindigkeitskontrolle mit Lichtschranken
[Bearbeiten]
Der ein oder andere, der schon einmal geblitzt worden ist, ist unbewusst mit dem Mittelwertsatz in Berührung gekommen. Zumindest wenn es sich um einen Blitzer Lichtschranken-Technik gehandelt hat. Stell dir vor, du fährst mit dem Auto auf einer Landstraße. Die zulässige Höchstgeschwindigkeit beträgt . Die zurückgelegte Strecke deines Autos ist durch die differenzierbare Ortsfunktion gegeben, die von der Zeit abhängt. Dabei entspricht die Ableitung der Ortsfunktion zum Zeitpunkt der momentanen Geschwindigkeit, d.h. . Bei einer Geschwindigkeitsmessung mit Lichtschranken durchfährt man zwei Lichtschranken, die an zwei festen Streckenpunkten und platziert sind. Passierst man die beiden Lichtschranken zu den Zeitpunkten und , so beträgt die Durchschnittsgeschwindigkeit zwischen diesen beiden Messpunkten
Da die Ortsfunktion die Voraussetzungen des Mittelwertsatzes erfüllt, gibt es einen Zeitpunkt mit
Die gemessene Durchschnittsgeschwindigkeit zwischen den beiden Schranken muss man also mindestens zu einem Zeitpunkt gefahren sein. Ist nun , wobei eine gewisse Toleranzgrenze ist (üblicherweise 3%), so wird man geblitzt und zur Kasse gebeten! ![]() Um Fehlmessungen zu vermeiden, werden in der Praxis mehr als zwei Lichtschranken verwendet und mehr als eine Messung durchgeführt. Das Prinzip bleibt aber dasselbe. Eine weitere Technik zur Geschwindigkeitsmessung beruht im Übrigen auf dem Doppler-Effekt und verwendet ein Radar zur Ermittlung der Geschwindigkeit.
Um Fehlmessungen zu vermeiden, werden in der Praxis mehr als zwei Lichtschranken verwendet und mehr als eine Messung durchgeführt. Das Prinzip bleibt aber dasselbe. Eine weitere Technik zur Geschwindigkeitsmessung beruht im Übrigen auf dem Doppler-Effekt und verwendet ein Radar zur Ermittlung der Geschwindigkeit.
Zweiter Mittelwertsatz
[Bearbeiten]Es gibt eine weitere Variante des Mittelwertsatzes, welcher zweiter oder auch verallgemeinerter Mittelwertsatz genannt wird. Deswegen wird der „normale“ Mittelwertsatz auch erster Mittelwertsatz genannt. Wir werden sehen, dass auch der zweite Mittelwertsatz aus dem Satz von Rolle folgt. Für die zweite Variante benötigen wir neben unserer Funktion noch eine Funktion , die ebenfalls die Voraussetzungen des Mittelwertsatzes erfüllt. Der zweite Mittelwertsatz ist nützlich, da sich aus ihm die Regel von L'Hospital herleiten lässt.
Satz und Beweis
[Bearbeiten]Satz (Zweiter Mittelwertsatz)
Seien zwei stetige Funktionen, die auf differenzierbar sind. Weiter sei für alle . Dann ist und es existiert ein mit
Beweis (Zweiter Mittelwertsatz)
Angenommen es gilt , so gibt es nach dem Satz von Rolle ein mit . Dies widerspricht der Voraussetzung des Satzes, dass für alle die Ungleichung gilt und so muss gelten. In Analogie zur Hilfsfunktion aus dem Beweis zum Mittelwertsatz, wählen wir hier die Hilfsfunktion
Diese ist auf stetig und auf differenzierbar, als Komposition stetiger bzw. differenzierbarer Funktionen. Außerdem gilt . Damit ist der Satz von Rolle anwendbar, und es gibt ein mit
Dies ist äquivalent zu .
Aufgabe zum zweiten Mittelwertsatz
[Bearbeiten]Aufgabe (Gegenbeispiel zum zweiten Mittelwertsatz)
Betrachte die Polynomfunktionen
Zeige, dass kein existiert mit
Wie verträgt sich dieses Ergebnis mit dem zweiten Mittelwertsatz?
Lösung (Gegenbeispiel zum zweiten Mittelwertsatz)
Es gilt
Andereseits ist für alle :
Damit muss stets für alle sein. Nun muss für den zweiten Mittelwertsatz die Voraussetzung für alle erfüllt sein. Es ist auf stetig und folgende Ungleichungen gelten:
und
Nach dem Zwischenwertsatz gibt es daher ein mit . Also sind die Voraussetzungen des zweiten Mittelwertsatzes nicht erfüllt, und dieser kann somit hier nicht angewandt werden.
Bemerkungen
[Bearbeiten]Bemerkung 1: Offensichtlich erhalten wir für den ersten Mittelwertsatz aus dem Zweiten. Den Zweiten haben wir aber aus dem Satz von Rolle gefolgert. Da der erste Mittelwertsatz und der Satz von Rolle äquivalent sind, folgt also auch der zweite Mittelwertsatz aus dem Ersten. Die beiden Mittelwertsätze sind daher äquivalent.
Bemerkung 2: Lassen wir die Voraussetzung für alle weg, so gilt der zweite Mittelwertsatz immer noch in der Form
Verständnisfrage: Warum gilt der zweite Mittelwertsatz auch in dieser allgemeineren Form?
Angenommen, es gibt (mindestens) ein mit . Gilt außerdem , so gibt es mit dem Satz von Rolle ein mit , und auf beiden Seiten der Gleichung steht Null. Gilt , so funktioniert der Beweis analog zu dem oben mit der Hilfsfunktion .
Übersicht der Folgerungen aus den Mittelwertsätzen
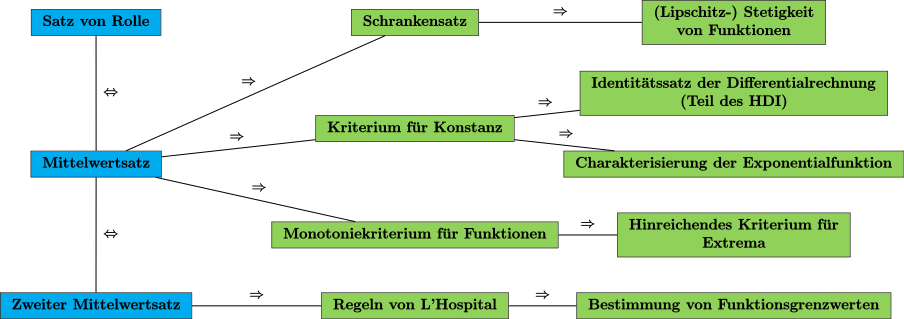
[Bearbeiten]In der Einleitung hatten wir schon erwähnt, dass sich aus den Mittelwertsätzen zahlreiche wichtige Resultate folgern lassen.
- Wir haben den Schrankensatz für differenzierbare Funktionen mit beschränkter Ableitung bewiesen. Mit diesem lässt sich die Lipschitz-Stetigkeit zahlreicher Funktionen beweisen.
- Eine weitere praktische Folgerung ist das Kriterium für Konstanz. Dieses besagt, dass eine Funktion konstant ist, falls ist (Die Ableitung ist konstant Null). Damit können wir den Identitätssatz der Differentialrechnung herleiten. Dieser sagt aus, dass sich zwei Funktionen mit identischer Ableitung lediglich um eine Konstante unterscheiden. Er ist ein wesentlicher Bestandteil des Hauptsatzes der Differential- und Integralrechnung. Eine weitere Konsequenz aus dem Kriterium für Konstanz ist die Charakterisierung der Exponentialfunktion über die Differentialgleichung .
- Ebenso lässt sich mit dem Mittelwertsatz das Monotoniekriterium für differenzierbare Funktionen beweisen. Dieses stellt einen Zusammenhang zwischen dem Monotonieverhalten der Funktion und dem Vorzeichen der Ableitungsfunktion her. Genauer ist genau dann monoton steigend (bzw. fallend), falls (bzw. ) ist. Daraus kann man ein hinreichendes Kritrerium für die Existenz eines Extremums einer Funktion in einem Punkt herleiten.
- Aus dem zweiten Mittelwertsatz können die Regeln von L'Hospital gefolgert werden. Mit deren Hilfe lassen sich zahlreiche Grenzwerte von Quotienten zweier Funktionen mit Hilfe der Ableitung berechnen.
Die aufgeführten Punkten sind im folgenden Übersichtsdiagramm zusammengefasst:



![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)














![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)














![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)



![{\displaystyle H:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8df43c0e303136cb915539221cc9ff141727b5)





![{\displaystyle H:[a,b]\to \mathbb {R} ,\ H(x)=f(x)-{\tfrac {f(b)-f(a)}{b-a}}(x-a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93175c5a90eaad13904db32ce8dc945043727007)
![{\displaystyle {\begin{aligned}H(a)&=f(a)-{\frac {f(b)-f(a)}{b-a}}(a-a)\\[0.5em]&=f(a)\\[0.5em]&=f(b)-(f(b)-f(a))\\[0.5em]&=f(b)-{\frac {f(b)-f(a)}{b-a}}(b-a)=H(b)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/171d10772a21b61f6e646c471d7ebf7df37ad7c6)







![{\displaystyle f:[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2de6d0d4c98d4ca7ad937c772dc3e3e914b062f5)


![{\displaystyle f':[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d30b7ed7936385475d9d8173c519fd9b7937b3a7)







![{\displaystyle [0,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/725684c883c7ef386e8a0fe4d111e72c565747ed)










![{\displaystyle {\begin{aligned}&&\ln(x)&<x-1\\[0.3em]&\iff {}&{\frac {\ln(x)}{x-1}}&<1\\[0.3em]&\iff {}&{\frac {\ln(x)-\ln(1)}{x-1}}&<1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c8f57dc021e05c29b46571f163315655f37e77e)


![{\displaystyle \ln :[1,x]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59d5dca9f8ac103b841870fc529b38449155993)








![{\displaystyle {\begin{aligned}&&1-{\frac {1}{x}}&<\ln(x)\\[0.3em]&\iff {}&{\frac {x-1}{x}}&<\ln(x)\\[0.3em]&\iff {}&{\frac {1}{x}}&<{\frac {\ln(x)}{x-1}}\\[0.3em]&\iff {}&{\frac {1}{x}}&<{\frac {\ln(x)-\ln(1)}{x-1}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8098ee1cf385d5edccd5eb34c56011c4bc554dbe)



![{\displaystyle f:[1,x]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae5a5dec32656c8990c6f05e3f809f5cf6f4036f)

![{\displaystyle [1,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63470e8fe9faf7ae30b257d12486bf1730330e5f)

![{\displaystyle {\begin{aligned}&&f'(\xi )&={\frac {f(x)-f(1)}{x-1}}\\[0.3em]&\iff {}&\ln '(\xi )&={\frac {\ln(x)-\ln(1)}{x-1}}\\[0.3em]&\iff {}&{\frac {1}{\xi }}&={\frac {\ln(x)}{x-1}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41b93e44c00194c78125aef7879c19a0ee07ae6f)
![{\displaystyle {\begin{aligned}&&{\frac {\ln(x)}{x-1}}={\frac {1}{\xi }}&{\overset {\xi >1}{<}}{\frac {1}{1}}=1\\[0.3em]&\iff {}&\ln(x)&<x-1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bafecc04a3a51865c64d28d1d83b0dbc0f31b72)

![{\displaystyle {\begin{aligned}&&{\frac {\ln(x)}{x-1}}&={\frac {1}{\xi }}{\overset {\xi <x}{>}}{\frac {1}{x}}\\[0.3em]&\iff {}&\ln(x)&>{\frac {x-1}{x}}=1-{\frac {1}{x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ba92153fe95794a5e32d0b36538c904c64b9db8)











![{\displaystyle x,y\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e14f38807bc231b9e43d45c8e909d463afb17b5)

![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)









![{\displaystyle {\begin{aligned}|(\sin )'(x)|&=|\cos(x)|\leq 1\\[0.3em]|(\cos )'(x)|&=|\sin(x)|\leq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01a9da11a276c61246d359dd92c9fd2e9a4e6076)






![{\displaystyle x,{\tilde {x}}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73eb4a9707daa29cfced5f7ec72abbdad44b149c)












![{\displaystyle s:[t_{0},t_{1}]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8eab7f810b860ef99b58cb9d813f0471a88404)





![{\displaystyle f,g:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e569de0fc730b7a75b46b6fd57598e0c94712f91)





![{\displaystyle F:[a,b]\to \mathbb {R} ,\ F(x)=f(x)-{\tfrac {f(b)-f(a)}{g(b)-g(a)}}(g(x)-g(a))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d038fe996fbc6b232d47850228e8b8db09b689a6)



![{\displaystyle {\begin{aligned}f:[0,1]\to \mathbb {R} ,\ f(x)=3x^{4}-2x^{3}-x^{2}+1\\g:[0,1]\to \mathbb {R} ,\ g(x)=4x^{3}-3x^{2}-2x\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87f633b17bc7f1e9c6467f0524c5b20e2fde56f5)






![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)














