Astronomische Berechnungen für Amateure/ Positionsastronomie/ Koordinatentransformationen
Horizontsystem und festes Äquatorsystem
[Bearbeiten]Mit den sechs im letzten Kapitel vorgestellten Formelgruppen haben wir das nötige Rüstzeug, um Koordinaten, die in einem bestimmten Koordinatensystem gegeben sind, in ein anderes System umzurechnen. Im folgenden soll diese Umrechnung am Beispiel der Umwandlung vom Horizontsystem ins feste Äquatorsystem exemplarisch durchgeführt werden. Für die übrigen Umrechnungen geben wir nur noch das Ergebnis an. Die Herleitung überlassen wir Ihnen als geneigtem Leser.

Die beiden Pole von Horizontsystem (Zenit Z) und festem Äquatorsystem (Himmelsnordpol N) bilden zusammen mit dem Objekt O, dessen Koordinaten vom einen ins andere System umgerechnet werden sollen, ein sphärisches Dreieck. Sind [τ; δ] die festen Äquatorkoordinaten Stundenwinkel und Deklination des Objektes; [A; h] bzw. [A; z] die Horizontkoordinaten Azimut und Höhe bzw. Zenitdistanz; ϕ die geografische Breite des Beobachters, dann gilt im sphärischen Dreieck ZNO: ZN = 90° – ϕ; ZO = z = 90° – h; NO = 90° – δ für die drei Seiten. Zwei Winkel hängen mit Koordinaten zusammen: . Wir wenden auf dieses Dreieck den Seiten-Cosinussatz an und erhalten:
Aus der ebenen Trigonometrie ist bekannt, dass sin(90° – x) = cos x und cos(90° – x) = sin x. Damit finden wir:
Sind die Koordinaten [τ; δ] im festen Äquatorsystem und die geografische Breite ϕ bekannt, lässt sich mit dieser Gleichung die Zenitdistanz oder die Höhe berechnen. Zur Berechnung des Azimutes wenden wir den Cotangenssatz auf das Dreieck ZNO an:
Aus der ebenen Trigonometrie ist weiterhin bekannt, dass cot(90° – x) = tan x und cot(180° – x) = –cot x, und dass der Cotangens eines Winkels der Kehrwert des Tangens von eben diesem Winkel ist. Damit finden wir:
Lösen wir nach tan A auf, so erhalten wir eine Gleichung, mit deren Hilfe wir bei Kenntnis der Koordinaten im festen Äquatorsystem und der geografischen Breite das Azimut berechnen können:
Beispiel:
Welche Koordinaten hat der Himmelsnordpol im Horizontsystem, wenn er im festen Äquatorsystem die Koordinaten δ = 90° und τ = 0° hat? Der Stundenwinkel ist willkürlich, denn eigentlich ist er unbestimmt. Setzen wir ein, so finden wir cos z = sin h = sin ϕ, woraus wir h = ϕ bzw. z = 90° – ϕ finden. Für das Azimut erhalten wir , denn . Daraus finden wir A = 180°. Wir erkennen nun auch den Vorteil, dass wir zur Bestimmung des Azimuts eine Formel mit dem Tangens gewählt haben. Betrachten wir jeweils Zähler Z und Nenner N separat, können wir eindeutig festlegen, in welchem Quadranten der Winkel liegt:
- Z > 0, N > 0 : A liegt im ersten Quadranten, d. h. 0° ≤ A ≤ 90°; A = arctan(Z/N)
- Z > 0, N < 0 : A liegt im zweiten Quadranten, d. h. 90° < A ≤ 180°; A = 180° + arctan(Z/N)
- Z < 0, N < 0 : A liegt im dritten Quadranten, d. h. 180° < A ≤ 270°; A = 180° + arctan(Z/N)
- Z < 0, N > 0 : A liegt im vierten Quadranten, d. h. 270° < A < 360° ; A = 360° + arctan(Z/N)
Für die umgekehrte Transformation wählen wir wieder den Seiten-Cosinussatz und den Cotangenssatz, jetzt aber mit einer anderen Kombination der Bestimmungsstücke:
womit wir sofort finden:
Für den Stundenwinkel finden wir mit dem Cotangenssatz:
woraus wir ableiten:
Beispiel:
Welche Koordinaten hat der Zenit (h = 90° bzw. z = 0°; A = 0° – wiederum willkürlich festgelegt). Wir finden sin δ = sin ϕ, also δ = ϕ. Mit analogen Überlegungen wie oben finden wir: τ = 0° = 0h.
Zusammengefasst: Für die Umrechnung zwischen dem Horizontsystem und dem festen Äquatorsystem gelten die Formeln:
Umwandlung von festen Äquatorkoordinaten in Horizontkoordinaten:
Umwandlung von Horizontkoordinaten in Äquatorkoordinaten:
![]() Sprung zurück nach oben.
Sprung zurück nach oben.
Festes Äquatorsystem und rotierendes Äquatorsystem
[Bearbeiten]Dies ist eine einfache Umwandlung, aber eine wichtige: über diese Umwandlung werden astronomische Koordinaten mit den Zeitsystemen verknüpft. Die wichtigsten Aussagen in diesem Zusammenhang:
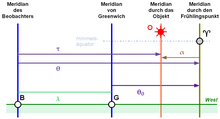
Der Stundenwinkel τ des Frühlingspunktes ist gleich der lokalen Sternzeit θ. Der um 12 Stunden (180°) erhöhte Stundenwinkel der Sonne ist gleich der Ortszeit.
Handelt es sich um die mittlere Sonne, dann ist es mittlere Ortszeit MOZ. Handelt es sich um die wahre Sonne, dann ist es die wahre Ortszeit WOZ:
Handelt es sich um den mittleren Frühlingspunkt, dann ist es die mittlere Sternzeit. Handelt es sich um den wahren (bzw. scheinbaren) Frühlingspunkt, dann ist es die scheinbare Sternzeit. Damit ist auch der Begriff „Gleichung des Äquinoktiums“ für die Differenz zwischen den beiden verständlicher, handelt es sich beim Frühlingspunkt doch um den Punkt, in dem die Sonne sich zum Zeitpunkt der Frühlings-Tag-und-Nachtgleiche aufhält.
Die Zusammenhänge zwischen den verschiedenen Systemen wird in der nebenstehenden Figur illustriert. Beachten Sie aber, dass es sich beim geografischen und dem rotierenden Äquatorsystem um rechtshändige Systeme handelt, beim festen Äquatorsystem aber um ein linkshändiges System.
Zusammengefasst gilt für die Beziehung zwischen α und τ (δ ist ohnehin in beiden Systemen gleich).
mit θ der Ortssternzeit und θ0 der Sternzeit in Greenwich; λ der geografischen Länge, positiv nach Osten, negativ nach Westen.
Anders formuliert:
Die Sternzeit entspricht derjenigen Rektaszension, welche gerade kulminiert.
![]() Sprung zurück nach oben.
Sprung zurück nach oben.
Rotierendes Äquatorsystem und Ekliptiksystem
[Bearbeiten]Nicht selten muss man zuerst rechtwinklige Ekliptikkoordinaten in polare Ekliptikkoordinaten umwandeln:
Dann gilt für die Umwandlung der beiden Koordinatensysteme (den Beweis mit Hilfe des Poldreiecks analog der Umwandlung vom Horizontsystem ins feste Äquatorsystem überlassen wir wie angekündigt Ihnen als Leser):
Umwandlung von Äquatorkoordinaten in Ekliptikkoordinaten:
Umwandlung von Ekliptikkoordinaten in Äquatorkoordinaten:
ε ist die Schiefe der Ekliptik, also der Winkel zwischen der Ekliptik und dem Himmelsäquator. Die Standardepochen sowie der Typ der Koordinaten muss jeweils übereinstimmen: sind z.B. α und δ auf die Standardepoche J2000.0 bezogen, dann müssen es auch λ, β und ε sein. Die mittlere Schiefe der Ekliptik hat für die Standardepoche J2000.0 den Wert ε = 23° 26' 21.406"[1]. Werden jedoch scheinbare Koordinaten verwendet, dann ist auch die wahre Schiefe der Ekliptik für die Umwandlung zu benutzen.
![]() Sprung zurück nach oben.
Sprung zurück nach oben.
Rotierendes Äquatorsystem und galaktisches System
[Bearbeiten]Die Koordinaten des galaktischen Pols und des Ursprungs der Längenzählung wurde von der IAU per Definition festgelegt, die Koordinaten α1950 = 12h 49m = 192{,}25° und δ1950 = +27 24' des galaktischen Nordpols sind also genaue, nicht ungefähre Werte. Bevor Äquatorkoordinaten ins galaktische System umgewandelt werden können, müssen sie auf die Standardepoche B1950.0 umgewandelt werden. Umgekehrt stehen Koordinaten nach der Umwandlung vom galaktischen System ins Äquatorsystem in der Standardepoche B1950.0 zur Verfügung und müssen nach Bedarf in die gewünschte Standardepoche umgewandelt werden.
Umwandlung vom rotierenden Äquatorsystem zur Standardepoche B1950.0
ins galaktische System:
Umwandlung vom galaktischen System ins rotierende Äquatorsystem
zur Standardepoche B1950.0
![]() Sprung zurück nach oben.
Sprung zurück nach oben.
Beispiel 1
[Bearbeiten]Aufgabe: Ein Beobachter sieht den Stern Wega im Zenit. Berechne Azimut und Zenitdistanz des Sterns Altair.
Daten (in Grad):
Wega:
Altair:
Damit man Wega im Zenit sehen kann, muss die geogr. Breite des Beobachters der Deklination von Wega entsprechen und die Rektaszension von Wega kulminieren. Es gilt daher:
sowie
Die kluminierende Rektaszension entspricht der Sternzeit
Der Stundenwinkel von Altair berechnet sich:
Wir haben zusammengefasst für Altair also die festen Äquatorkoordinaten
Umrechnen in Horizontale Koordinaten:
Zenitabstand zA von Altair:
und damit
bzw.
Azimut AA von Altair:
Mit Zähler:
und Nenner:
gilt:
Ergebnis:
Der Stern Altair hat einen Azimut von 326,9° und eine Zenitdistanz von 34,2°
Beispiel 2
[Bearbeiten]Der Hauptstern des Sternbildes Jungfrau ist Spica, α Vir, HD 116658, SAO 157923 hat die Koordinaten α2000 = 13h 25m 11.601s = 201.298338°, δ2000 = –11° 9' 40.64" (α1950 = 13h 22m 33.301s = 200.638754°, δ1950 = –10° 54' 3.36"). Berechnen Sie die mittleren Koordinaten dieses Sterns in den übrigen Koordinatensystemen für den Ort Wildspitz (LV03-Koordinaten 686490/215460/1580) am 5. April 2007 um 22:45 h MESZ. Lassen Sie die Eigenbewegung (noch) unberücksichtigt.
Lösung:
Es ist UT = 22:45h – 2h = 20.75h, somit JD = 2454196.364583. Für die geografischen Koordinaten finden wir λ = 8° 34' 39.52", ϕ = +47° 5' 4.2", H = 1628 m. Mit diesen Daten finden wir für die mittlere Ortssternzeit zum Zeitpunkt 22:45h MEZ θ = 10h 14m 23.7s. Aus einem Jahrbuch entnehmen wir für die Schiefe der Ekliptik ε = 23° 26' 27.4". Damit sind alle Parameter bereit, um die Umwandlungen vornehmen zu können:
Umwandlung vom rotierenden ins feste Äquatorsystem ergibt:
- δ = –11° 9' 40.64; τ = 20.82003h = 20h 49m 12.1s = 312.30042°
Umwandlung vom festen Äquatorsystem ins Horizontsystem ergibt:
- h = 17.84295° = 17° 50' 35", z = 72° 9' 25", A = 310° 21' 21"
Umwandlung vom rotierenden Äquatorsystem ins Ekliptiksystem ergibt:
- β = –2.05375° = –2° 4' 47", λ = 203.84147° = 203° 50' 29"
Spica hat eine so geringe ekliptikale Breite, dass sie immer wieder vom Mond und gelegentlich – wenn auch sehr selten – auch von Planeten bedeckt wird.
Umwandlung vom rotierenden Äquatorsystem in das galaktische System ergibt:
- b = 50.84483° = 50° 50' 41", x = 346.88663°; l = 316.11337° = 316° 6' 48"
![]() Sprung zurück nach oben.
Sprung zurück nach oben.
Die Ekliptik am Horizont
[Bearbeiten]Zwischen der Ekliptik und dem Horizont gibt es wie immer zwischen zwei Grosskreisen zwei Schnittpunkte. An einem gegebenen Ort und zu gegebener Zeit, dh. die Grössen geografische Breite ϕ, lokale Sternzeit θ und Schiefe der Ekliptik ε sind bekannt, haben diese beiden Punkte die ekliptikale Länge λ
Die beiden Grosskreise schliessen am Horizont den Winkel I ein, der sich wie folgt berechnen lässt:
Im Laufe eines Tages variiert θ zwischen 0 und 24h bzw. 0 und 2π. Falls θ = +π/2 ist, erhält cos I den kleinstmöglichen Wert. Falls θ = 3π/2 ist, erhält cos I den grösstmöglichen Wert. Daraus folgt für Orte auf der Nordhalbkugel
Verwechseln Sie I nicht mit dem Winkel, unter die Sonne oder ein anderer Himmelskörper über den Horizont steigt. Dies ist gleich dem Winkel, den der entsprechende Deklinationskreis – ein Breitenkreis – mit dem Horizont bildet. I wird benötigt, wenn man abschätzen will, um wieviel ein Objekt auf der Ekliptik am folgenden Tag später auf- oder untergeht.
![]() Sprung zurück nach oben.
Sprung zurück nach oben.
Allgemeines zu Koordinatentransformationen
[Bearbeiten]Koordinatentransformation können im allgemeinen Fall aus einer Verschiebung des Ursprungs (Translation), einer Drehung (Rotation), einer Skalierung oder einer Scherung bestehen. Scherungen – dh. Überführung in ein Koordinatensystem mit nicht mehr rechtwinkligen Achsen – spielen in der klassischen Physik – die für Amateure relevant ist – praktisch keine Rolle. Neuskalierungen passieren immer dann, wenn man den Massstab ändert, z.B. von AE auf km oder ly bzw. pc. In der Praxis des Amateurs sind es vor allem die Translation und die Rotation, die eine Rolle spielen:
- Eine Translation muss immer dann erfolgen, wenn der Ursprung von altem und neuem Koordinatensystem nicht übereinstimmen. Dies ist z.B. der Fall beim Wechsel von geozentrischen ekliptikalen Koordinaten zu heliozentrischen ekliptikalen Koordinaten oder beim Wechsel vom geozentrischen (bzw. baryzentrischen) festen Äquatorsystem zum topozentrischen festen Äquatorsystem.
- Eine Rotation spielt in fast allen besprochenen Koordinatentransformationen eine Rolle: Horizontsystem und festes Äquatorsystem haben als gemeinsame Achse jene Achse, die vom Beobachter zum Westpunkt am Horizont weist. Werden die erste und dritte Achse um den Winkel 90° – ϕ um die gemeinsame Achse gedreht, so wird das eine System ins andere überführt. Bei Ekliptik- und rotierendem Äquatorsystem ist es eine Drehung um den Winkel ε um die gemeinsame erste Achse, die zum Frühlingspunkt weist.
Translationen lassen sich besonders einfach mit Hilfe von Vektoren beschreiben. Hat ein Objekt in einem ersten Koordinatensystem den Ortsvektor , in einem zweiten Koordinatensystem dagegen , und hat der Ursprung des zweiten Koordinatensystems im ersten den Ortsvektor , dann gilt die Beziehung
Beispiel:
Zu einem bestimmten Zeitpunkt hat Mars die heliozentrischen ekliptikalen Koordinaten λ = 271° 09' 19.5", β = –1° 13' 49.5", r = 1.452 4326 AE; zum gleichen Zeitpunkt hat die Sonne die geozentrischen Koordinaten X⊙ = +0.783 7432; Y⊙ = +0.632 4494; Z⊙ = –0.000 0007. Wie lauten die geozentrischen ekliptikalen kartesischen Koordinaten des Mars? Mit der aktuellen Schiefe der Ekliptik ε = 23° 26' 36.146" sollen anschliessend noch die geozentrischen Koordinaten im rotierenden Äquatorsystem berechnet werden.
Zuerst berechnen wir aus den heliozentrischen Polarkoordinaten des Mars seine rechtwinkligen heliozentrischen Koordinaten. Es ist XM = r ∙ cos λ ∙ cos β = +0.029 2808, YM = r ∙ sin λ ∙ cos β = –1.451 8025, ZM = r ∙ sin β = –0.031 1883. Zur Kontrolle: r ist tatsächlich 1.452 4326 (berechnet aus [X, Y, Z]). Das heliozentrische System ist das erste, das geozentrische das zweite System. Gegeben ist in diesem Fall mit den geozentrischen Sonnenkoordinaten also nicht , sondern . Dann ist mit den gegebenen Grössen:
Wie weiter oben ausgeführt, lassen sich daraus die geozentrischen ekliptikalen Koordinaten berechnen: ekliptikale Länge λ' = 314° 46' 40.28", ekliptikale Breite β' = –1° 32' 52.03". Im weiteren ergibt sich für den geozentrischen Abstand des Mars Δ = 1.154 6948. Mit dem gegebenen Wert der Schiefe der Ekliptik findet man für die Rektaszension α = 21h 10m 52s, für die Deklination δ = –17° 53' 01".
![]() Sprung zurück nach oben.
Sprung zurück nach oben.
Nachweis:
- ↑ IAU XXV GA 2006

























































![{\displaystyle {\overrightarrow {r_{0}}}\;=\;[X_{0},Y_{0},Z_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a489c81acdea21ad32aef36c15a3c73edbc44fe)
![{\displaystyle {\overrightarrow {r_{0}'}}\;=\;[X_{0}',Y_{0}',Z_{0}']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a425263ddd8b31ed305ffc06a532814627d9d214)
![{\displaystyle {\vec {a}}\;=\;[a_{x},a_{y},a_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2629ab8a641dd3b4308e9221d2eda9bb9bfd4f75)
![{\displaystyle {\overrightarrow {r_{0}'}}\quad =\quad {\overrightarrow {r_{0}}}\;-\;{\vec {a}}\quad =\quad [X_{0}-a_{x},Y_{0}-a_{y},Z_{0}-a_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60fc7d485349002a0d79aa3a64431a9409b135e5)




