Aufgabensammlung Physik: Kürzester Weg auf Ebene
Erscheinungsbild
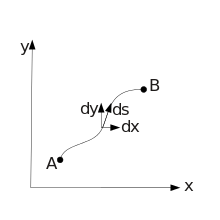
Finde mittels der Variation der Kurve, nach den Prinzipien der Variationsrechnung den kürzesten Weg S zwischen den Punkten A und B auf einer homogenen Ebene.
1. Finde die Funktionenschar
Formuliere den allgemeinen Integranden in eine für das Problem geeignete Form um. Wie würdest Du die Teilstrecke mathematisch formulieren?
Lösung der Aufgabe 1
kann in karthesischen Koordinaten nach dem Satz des Pythagoras wie folgt dargestellt werden:
2. Aufstellen der Eulerschen Gleichung
Stelle nun zunächst das Integral für den Weg auf.
Stelle dann die Eulersche Gleichung auf und löse diese.
Lösung der Aufgabe 2
- Die Eulersche Gleichung lautet:
- Dabei ist:
- Damit folgt und somit
- Sei . Es folgt
- Wegen ist für bestimmte und damit ist eine Gerade.










![{\displaystyle {\begin{aligned}{\begin{array}{rrl}&{\frac {y'}{\sqrt {1+y'^{2}}}}&=c\\\Rightarrow \ &y'&=c{\sqrt {1+y'^{2}}}\\\Rightarrow \ &y'^{2}&=c^{2}\cdot (1+y'^{2})\\\Rightarrow \ &(1-c^{2})\cdot y'^{2}&=c^{2}\\&&\left\downarrow \ {\begin{array}{l}{\text{Wegen }}|{\sqrt {1+y'^{2}}}|>|y'|{\text{ ist }}|c|<1\\[5px]{\text{und damit }}1-c^{2}>0\end{array}}\right.\\\Rightarrow \ &y'^{2}&={\frac {c^{2}}{1-c^{2}}}\\\Rightarrow \ &|y'|&={\sqrt {\frac {c^{2}}{1-c^{2}}}}\\&&\left\downarrow \ {\begin{array}{l}y'{\text{ ist stetig und damit kann }}y'{\text{ nicht zwischen}}\\[5px]{\sqrt {\frac {c^{2}}{1-c^{2}}}}{\text{ und }}-{\sqrt {\frac {c^{2}}{1-c^{2}}}}{\text{ springen}}\end{array}}\right.\\\Rightarrow \ &y'&=\mathrm {const} \\\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4734c8d81d4098274cc7dd1f22d007f840b7e41c)



