C++-Programmierung/ Eine Matrix-Bibliothek – mitrax/ Zielstellung
In diesem Kapitel wollen wir eine Bibliothek zum Arbeiten mit Matrizen entwickeln. Bei dieser Gelegenheit werden einige fortgeschrittene Programmiertechniken vorgestellt. Außerdem soll der Leser einen ersten Eindruck gewinnen, was bei der praktischen Entwicklung beachtet werden muss. Wenn Sie Schwierigkeiten haben sollten, den Werdegang nachzuvollziehen, dann sollten Sie sich möglicherweise die vorangegangen Kapitel noch einmal genauer anschauen, da hier nicht mehr auf jede Kleinigkeit hingewiesen wird. Dies ist notwendig, um den Text kompakt und übersichtlich zu halten, denn sonst werden sich Leser, welcher der fortgeschrittenen Zielgruppe dieses Kapitels angehören, unnötig langweilen und möglicherweise wichtige Hinweise zur eigentlichen Problemstellung überlesen. Alle Bestandteile von mitrax sollen im Namensraum mitrax stehen. Darauf wird in den folgenden Kapiteln jedoch ebenfalls nicht mehr explizit hingewiesen.
mitrax – Namensherkunft
[Bearbeiten]
Das Projekt mitrax entstand als Semesterarbeit. Die Aufgabenstellung lautete in groben Zügen, man entwickle eine Klasse welche Matrizen (im mathematischen Sinne) repräsentiert. Dabei sollten insbesondere einige Rechenoperatoren überladen werden und die Klasse sollte als Template, unabhängig vom konkreten Typ ihrer Elemente, nutzbar sein. Da sich während der Entwicklung herauskristallisierte, dass sich das Ergebnis hervorragend als Lehrbeispiel eigenen würde, entstand parallel auch dieser Abschnitt.
Der Name „mitrax“ entstand durch zufälliges Vertauschen der Buchstaben von „matrix“. Dadurch ergibt sich, nach Entfernen des Buchstabens „x“ am Ende, ein Wort, das in der Biologie eine Gattung innerhalb der Familie der Mitridae (auch Mitraschnecken genannt) bezeichnet. Da deren Gestalt zwar immer ähnlich und dennoch abwechslungsreich ist, erinnern diese Tiere ein wenig an den Templatecharakter der Matrixklasse, auf den ja besonderen Wert gelegt wurde.
Konkretisierung der Aufgabenstellung
[Bearbeiten]In einem realen Entwicklungsprozess würde dieser Schritt gemeinsam mit dem Auftraggeber erfolgen. Da in unserem Fall jedoch kein solcher existiert, werden wir selbst festlegen, was sinnvollerweise möglich sein sollte.
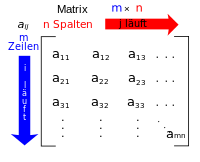
Zunächst machen wir uns Gedanken darüber, was eine Matrix eigentlich ist. Im wesentlichen handelt es sich dabei um rechteckige Anordnung von Elementen gleichen Typs. Sie enthält also eine Information über die Anzahl der Zeilen und die Anzahl der Spalten, sowie Anzahl Zeilen mal Anzahl Spalten viele Elemente des gleichen Typs. Die Anzahl der Zeilen und Spalten wird als Dimension der Matrix bezeichnet. Im deutschen spricht man in diesem Zusammenhang eigentlich vom Typ der Matrix, dieser Begriff würde jedoch ständig zu Verwechslungen mit C++-Typen führen, daher werden wir den Begriff Typ in diesem Abschnitt nicht verwenden.
Nun ist es Sinnvoll, wenn einzelne Zeilen und Spalten herausgegriffen werden können. Ein Zugriff auf ein konkretes Element sollte natürlich auch möglich sein. Diese Zugriffe werden wir mittels sogenannter Proxyklassen realisieren. Dies hat auch den Vorteil, dass der Zugriff auf einzelne Elemente, wie bei einem zweidimensionalen Array, durch zweimalige Anwendung des Indexoperators (operator[]()) durchgeführt werden kann.
Für viele Operationen ist die konkrete Anordnung eines Elements im Rechteck unwesentlich, da lediglich alle Elemente innerhalb der Matrix einmal verarbeitet werden müssen. Aus diesem Grund werden wir ein Iteratorinterface für die Matrixklasse und auch für die Proxyklassen anbieten. Die Nutzung von Iteratoren gibt einem Leser von Quellcode auch immer den Hinweis, dass es sich hier um eine elementweise Verarbeitung von Elemente handelt. Wir erhöhen somit potenziell die Lesbarkeit von Clientquellcode, also dem, was ein Nutzer unserer Bibliothek schreibt. Natürlich gilt dies ebenso für den Quellcode unserer Bibliothek, wenn wir das Iteratorinterface irgendwo nutzen.
Auf Matrizen können verschieden Rechenoperationen definiert werden. Wir wollen uns dabei auf die folgenden beschränken:
- Negation einer Matrix
- Addition / Subtraktion zweier Matrizen gleicher Dimension
- Multiplikation mit einem Skalar
- Division durch einen Skalar
- Matrixmultiplikation
- Transponieren
- Für quadratische Matrizen:
- Determinante
- Inverse Matrix
Diese Rechenoperationen werden nicht als Member der Matrixklasse implementiert, da sie nicht zu einer Matrix gehören, sondern auf Matrizen arbeiten. Sie werden also als nicht befreundete Nichtelementfunktionen deklariert. Dies hat nebenbei den gewaltigen Vorteil, dass ein Nutzer von mitrax selbst weitere Operationen im gleichen Stil schreiben kann. Syntaktisch wird in seinem Quellcode dann nicht direkt zu erkennen sein, ob es sich um eine native (von uns bereitgestellte) Funktion oder um eine selbst definierte handelt, was die Lesbarkeit seines Quellcodes erhöht. Einen Leser seines Codes würde es nur unnötig verwirren, wenn zwei anscheinend gleichberechtigte Operationen unterschiedlich aufgerufen werden müssten. Außerdem entspricht es auch dem Paradigma der objektorientierten Programmierung, das Funktionen, die keinen direkten Zugriff auf die internen Elemente einer Klasse benötigen, auch keinen haben. Die Daten sind dadurch stärker gekapselt.
Vielleicht ist ihnen bekannt, dass viele der Operationen auf Matrizen nur unter bestimmten Voraussetzungen ausgeführt werden können. So müssen beispielsweise zwei Matrizen, die addiert werden sollen, die gleiche Dimension besitzen. Anhand der Liste der Operationen, die wir definieren möchten, wird aber auch schon offensichtlich, dass bestimmte Operationen nur für quadratische Matrizen ausführbar sind, also solche, die die gleiche Anzahl von Zeilen und Spalten besitzen. Das führt uns dazu, dass wir eine ganze Reihe eigener Klassen zur Ausnahmebehandlung benötigen. Es wird zwar versucht, das Thema getrennt in einem eigenen Kapitel zu behandeln, jedoch treten in vielen Kapitel Situationen auf, für die eine Ausnahmebehandlung nötig ist. Daher sind hier einige Querverweise unumgänglich. Lassen Sie sich davon bitte nicht verwirren. Wenn Sie einen Hinweis zu diesem Thema an einer bestimmten Stelle noch nicht verstehen, dann lesen Sie erst mal weiter, in den meisten Fällen sollte irgendwann klar werden, was gemeint war.
Um etwas von unseren Matrizen zu sehen, benötigten wir natürlich eine Ein- und Ausgabe. Bei dieser Gelegenheit werden auch gleich ein paar eigene Manipulatoren für die Ausgabe einer Matrix bereitstellen. Das Format für die Ein- und Ausgabe sollte immer identisch sein, so dass wir eine ausgegebene Matrix auch später wieder einlesen können. Allerdings kann bei der Ausgabe mittels Whitespaces die Übersichtlichkeit für einen menschlichen Betrachter deutlich erhöht werden. So können etwa die einzelnen Elemente mit einer festen Mindestbreite ausgegeben werden. Auch eine zweidimensionale Ausgabe kann auf diesem Weg an und abgeschaltet werden. Es muss lediglich sichergestellt sein, dass der Eingabeoperator mit jeder möglichen Ausgabe zurechtkommt. Für die Proxyklassen werden wir ein eigenes Format festlegen.
Zum Abschluss möchten wir die Berechnungen noch einmal überarbeiten, so dass Sie verzögert ausgeführt werden. Das hat mehrere wesentliche Vorteile in Bezug auf die Performance. Zum einen müssen Berechnungen, deren Ergebnis nicht verwendet wird, auch niemals ausgeführt werden. Das ist gar nicht so selten der Fall, wie Sie vielleicht vermuten werden. Der zweite Vorteil besteht darin, dass längere Berechnungsketten in einem Durchlauf abgearbeitet werden können, anstatt für jede Operation ein eigenes temporäres Objekt anzulegen. Das spart Zeit und Speicherplatz. Als letzter Punkt wäre aufzuführen, dass die Prüfung der Dimensionskompatibilität für längere Berechnungsketten vorweg ausgeführt werden kann. Wenn ein Fehler festgestellt wird, dann beschwert sich das Programm sofort darüber und führt nicht erst Berechnungen von Zwischenergebnissen durch, die am Ende sowieso nicht weiterverarbeitet werden können. Das wird den Nutzern von mitrax vor allem in der Entwicklungsphase helfen, nicht unnötige Mengen von Kaffee zu konsumieren, während der Rechner arbeitet, nur um dann festzustellen, dass alles nochmal ausgeführt werden muss, weil sich am Ende ihres Programms ein logischer Fehler eingeschlichen hat.
