Einführung in die Systemtheorie/ Numerische Berechnung dynamischer Systeme

Numerische Berechnung dynamischer Systeme

Relativ einfache Übertragungssystem-Strukturen mit nichtlinearen Elementen sind durch konventionelle Rechenmethoden im kontinuierlichen Zeitbereich nicht mehr geschlossen lösbar. Mit handelsüblichen Personal-Computern kann das Verhalten beliebig vermaschter Systemstrukturen mittels numerischer Berechnung relativ einfach ausgeführt werden.

Vorteile der Simulation von Systemen mit Differenzengleichungen

• Einfache mathematische Anforderungen durch algebraische Operationen,
• Behandlung kombinierter LZI-Systeme mit nichtlinearen Systemen,
• Darstellung eines Regelkreises als Blockschaltbild mit Eintrag der Differenzengleichung und logischen Operatoren,
• Behandlung von mehrschleifigen Systemen (MIMO-Systeme),
• Einfache Lösung einer gewöhnlichen Differenzialgleichung höherer Ordnung mit Anfangswerten. Da es sich um bestimmte Integrale handelt, müssen keine Integrationskonstanten wie bei der klassischen Lösung einer homogenen Differenzialgleichung ermittelt werden.
• Bei tabellarischer Darstellung der Berechnung der einzelnen Teilsysteme völlige Durchsicht des inneren System-Bewegungsablaufs zum Beispiel eines Regelkreises. Bei Anwendung der Tabellenkalkulation unmittelbare grafische Darstellung der Systemausgangsgröße y(k) = f(k*∆t) mittels verfügbarer grafischer Werkzeuge.

Methode der numerischen Berechnung

Simulation dynamischer Systeme

Dynamische zeitinvariante Systeme mit konzentrierten Energiespeichern werden durch gewöhnliche Differenzialgleichungen vollständig beschrieben. Die Lösung der Differenzialgleichung, die Ausgangsgröße y(t), ist für ein gegebenes Eingangssignal u(t) eine Funktion der Zeit.

Werden die Differenziale der Ausgangsgröße y(t) einer Differenzialgleichung durch kleine Zeit-Differenzen (Differenzenquotienten Δy / Δt) als diskretisierte Zeit ersetzt, entsteht eine numerisch lösbare Differenzengleichung in Annäherung an die Differenzialgleichung.

Differenzengleichungen oder eine Kette von Differenzengleichungen, die mehrere hintereinander geschaltete Teilsysteme beschreiben, lassen die Ausgangsgröße algebraisch für einen kleinen Zeitschritt errechnen. Die numerische Gesamtlösung des Systems erfolgt - bei einfachen Differenzengleichungen - rekursiv (sich selbst aufrufend) über viele Berechnungsfolgen in je kleinen konstanten Zeit-Stufen. Die Form der Gesamt-Lösung ist damit tabellarisch. Alle Zeilen enthalten die gleichen Differenzengleichungen, alle Spalten berechnen die Folgen k (0, 1, 2, 3, ...k_MAX). Der gesamte betrachtete Zeitraum der numerischen Lösung beträgt $k_{MAX}\cdot \Delta t$ . Die Ausgangsgröße y(k, Δt) folgt in Amplituden-Stufen im zeitlichen Abstand Δt einer jeden Berechnungsfolge.

Die tabellarische Form der numerischen Lösung erlaubt auch die Berechnung nichtlinearer statischer Systeme, indem die nichtlineare Beziehung als Wertetabelle der Tabellenspalte der Folge k zugeordnet wird. Ebenso ist die Berechnung der Totzeit eines Systems durch Verschiebung der Zeilen mit geeigneten Programmbefehlen möglich.

Andere Methoden bedienen sich zur besseren Approximation z. B. an Stelle des Rechteck-Verfahrens (Explizites Eulerverfahren) des Trapezflächenverfahrens (Heun-Verfahren), des Mehrschrittverfahrens (Runge-Kutta-Verfahren) und anderer Verfahren.

Grund der aufwendigeren Approximationsverfahren ist die erzielbare höhere Genauigkeit und damit Reduzierung der Rekursionsfolgen, was bei langsamen Rechnern bei Echtzeitberechnungen erforderlich sein kann.

Digitale Regelung online

Bei Echtzeitberechnungen, beispielsweise mit einem programmierbaren digitalen Regler, der auf eine Hardware-Regelstrecke wirkt, wird die Diskretisierungszeit $\Delta t$ durch die "Abtastzeit" $T_{A}$ ersetzt.

Digitale Regler werden durch Mikrocomputer realisiert. Der Computer benötigt für die digitale Signalverarbeitung Ein- und Ausgangsschnittstellen, um das kontinuierliche Eingangssignal – die Regelabweichung – mittels A/D-Wandler zyklisch abzutasten und digital mit speziellen Programmiersprachen berechnen zu können. Der Mikrocomputer verarbeitet die abgetasteten Signalwerte als Eingangsfolgen mit Hilfe von Differenzengleichungen zu Ausgangsfolgen. Die so schrittweise errechneten Stellgrößen-Anteile jeder Komponente der Ausgangsfolge werden über einen D/A-Wandler und ein Halteglied wieder als feingestuftes quasi kontinuierliches Signal an die meist kontinuierlich wirkende Regelstrecke geliefert. Bei schnellen Regelstrecken spielen die Systemgeschwindigkeiten des Rechners, der A/D-D/A-Wandler, die Sample-and-Hold-Schaltung, wie auch die verwendeten Differenzengleichungen beziehungsweise deren Approximations-Algorithmen eine große Rolle.

Zeitdiskretisierung

Einfluss der Größe des Zeitintervalls ∆t auf die Berechnung (Euler rückwärts) eines Regelkreises mit Differenzengleichungen.

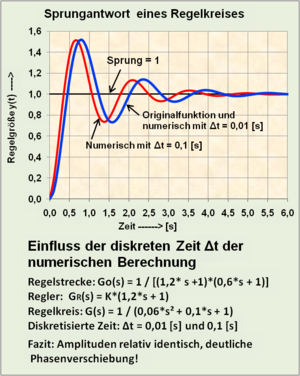
Die Zeitdiskretisierung eines dynamischen zeitinvarianten Übertragungssystems bedeutet der Übergang der Berechnung eines kontinuierlichen Systems f(t) mit unendlicher hoher Auflösung zu einem System f(k; ∆t) mit einer endlichen Auflösung eines fortlaufenden konstanten Zeitintervalls ∆t.

Bei der Simulation von dynamischen Übertragungsmodellen ist das diskrete Zeitintervall ∆t ein konstanter Zahlenwert, der unabhängig von der tatsächlichen Rechengeschwindigkeit des Rechners ist und mit der Berechnungsfolge k = (0, 1, 2, 3, ...k_MAX) ständig fortlaufend aufgerufen wird. Die aktuelle Zeit einer bestimmten Folge beträgt: $t=k\cdot \Delta t$

Das Zeitintervall ∆t muss genügend klein gegenüber der kleinsten Systemzeitkonstante sein, damit die Systembewegungen auch vollständig erfasst werden können, bzw. der Approximationsfehler gegenüber dem Verlauf der analytischen Funktion gering ist. ∆t muss kleiner als die kleinste Systemzeitkonstante T sein, anderenfalls ergeben sich zusätzlichen Berechnungsfehler.

Berechnungsfolge

Die Folge ist bestimmt, wenn die Beziehung der Anwendung (Bildungsgesetz) bekannt ist. Differenzengleichungen des Verfahrens "Euler-Rückwärts" werden rekursiv für ein Zeitintervall von k = 0 bis k_MAX fortlaufend berechnet.

In einer Folge k = (0, 1, 2, 3,…k_MAX) werden beliebig viele zeitdiskrete Einzelsysteme eines Gesamtsystems hintereinander für ein gleiches, konstantes Zeitintervall ∆t mittels Differenzengleichungen berechnet. Danach erfolgt die gleiche Berechnung der Einzelsysteme des Gesamtsystems mit der nächsthöheren Folge und bezieht sich dabei auf die vorhergehende Folge (k-1).

Für explizite (direkt, eindeutig) Approximationsalgorithmen bezieht sich die Ausgangsgröße eines Einzelsystems y_(k) auf die zurückliegende Folge y_(k-1).

Für implizite (mit enthalten, mit gemeint) Approximationsalgorithmen wird die unbekannte Ausgangsgröße y_(k+1) durch Iterationsverfahren bestimmt und auf y_(k) zurückgerechnet.

Jedes Einzelsystem mit dem Ausgangssignal y_(k) = f(System, k, ∆t, u_(k)) wird einzeln berechnet.

Für eine Systemkette unterschiedlichster Strukturen der gleichen Folge k ist jedes Ausgangssignal y_(k) eines Systems für das nachfolgende System das Eingangssignal u_(k). Das Eingangssignal u_(k) einer Systemkette ist meist ein Testsignal oder die Führungsgröße w_(k). Jedes Eingangssignal muss ebenfalls eine Funktion von ∆t und k eine zeitdiskrete Größe sein.

Anmerkung:

• Die mit Folge k bezeichnete Größe wird auch gelegentlich in der Fachliteratur auch mit n und das Zeitintervall ∆t mit T bezeichnet.

• Alle Signalgrößen wie zum Beispiel das System-Eingangssignal U(s) und das System-Ausgangssignal Y(s) im s-Bereich werden in der zeitdiskreten Darstellung als u_(k,Δt) und y_(k,Δt) dargestellt. Um die Indizierungen in den Differenzengleichungen noch übersichtlicher zu gestalten (wegen der Bezüge auf die Folgen k, k-1, k+1) werden für die Signalbezeichnungen die indizierte Größe der diskreten Zeit Δt fortgelassen. y_(k) und u_(k) bedeuten immer aktuelle Werte eines Signals einer unbestimmten Folge einer Differenzengleichung. Die Signale y_(k-1) und u_(k-1) bedeuten eine zurückliegende Folge gegenüber dem aktuellen Wert einer Signalfolge.

Analyse eines linearen zeitinvarianten Übertragungssystems

Beispiel einer Übertragungsfunktion der Polynomdarstellung und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:

$G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\dotsm +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\dotsm +a_{2}s^{2}+a_{1}s+a_{0}}}=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{(s-s_{p1})(s-s_{p2})\dotsm (s-s_{pn})}}$

Polynomdarstellungen G(s):

• Sind in der Polynomdarstellung alle Ableitungen und zugehörige Koeffizienten lückenlos mit positivem Vorzeichen vorhanden, stellt die Übertragungsfunktion für die Exponenten n > m ein zeitverzögerndes asymptotisch stabiles System dar.
• Fehlt das Absolutglied $a_{0}$ im Nennerpolynom ($a_{0}=0$), kann die Variable s aus dem Nennerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales integrierendes Systemverhalten" bezeichnet.
• Fehlt das Absolutglied $b_{0}$ im Zählerpolynom ($b_{0}=0$), kann die Variable s aus dem Zählerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales differenzierendes Systemverhalten" bezeichnet.
• Hat ein Teilsystem der Polynomdarstellung im Nenner bei der Polstellenzerlegung ein konjugiert-komplexes Polpaar $s_{p1;2}=-\delta \pm j\omega$, so stellt diese Übertragungsfunktion für die Exponenten n > m ein zeitverzögerndes asymptotisch stabiles, gedämpft schwingendes System dar.

Eine Nullstelle des Zählerpolynoms s_n oder ein Pol des Nennerpolynoms s_p kann bei Stabilität des Teilsystems (negativer Realteil der Pole und Nullstellen) folgende drei Formen von Zahlenwerten einnehmen:

Einfluss der Zahlenwerte von Nullstellen und Polen:

Nullstellen; Pole	Linearfaktoren in Pol- Nullstellendarstellung	Erklärung
${s_{n};s_{p}}=0$	$G_{1}(s)=s$	Absolutglied $a_{0}\ {\text{oder}}\ b_{0}$ des Polynoms fehlt
${s_{n};s_{p}}=\delta$	$G_{2}(s)=s-\delta$	Reeller Wert $\delta$ der Pole oder Nullstellen
${s_{n};s_{p}}=\delta \pm j\omega$	$G_{3}(s)=s-(\delta \pm j\omega )$	Konjugiert komplexer Wert der Pole oder Nullstellen

Der Realteil einer Nullstelle oder eines Poles wird üblich mit $\delta$ und der Imaginärteil mit $j\omega$ bezeichnet. Die angegebenen 3 Formen der Linearfaktoren können einfach und mehrfach auftreten.

Bei der Berechnung der Pole und Nullstellen aus Polynomen beispielsweise aus der gemischt quadratischen Gleichung (pq-Gleichung) können je nach Zahlenwerten reelle und konjugiert komplexe Werte entstehen. Die Polynome mit konjugiert komplexen Nullstellen oder Polen werden zur einfacheren Berechenbarkeit zu quadratischen Termen zusammengefasst, in denen nur reelle Koeffizienten auftreten.

Entstehung der Schwingungsgleichung im Nenner der Polynomdarstellung:

$G(s)={\frac {1}{[s-(\delta +j\omega )]\cdot [s-(\delta -j\omega )]}}={\frac {1}{s^{2}-2\cdot \delta \cdot s+\delta ^{2}+\omega ^{2}}}\ {\mathrel {\hat {=}}}\ {\frac {1}{s^{2}-p\cdot s+q}}$

Ein dynamisches System ist intern stabil, wenn alle (Teil-)Übertragungsfunktionen nur Pole in der linken s-Halbebene haben. Negative Zahlenwerte des reellen Anteils $\delta$ der Pole und Nullstellen bedeuten Stabilität des Teilsystems. Werden negative Zahlenwerte der Pole $s_{p}$ und Nullstellen $s_{n}$ eingesetzt, entstehen positive Linearfaktoren. Bei stabilen Systemen ist der Wert von $\delta$ negativ.

Die konjugiert komplexe Polstelle mit negativem Realteil lautet:

$s_{p1;2}=-\delta \pm j\omega$

Damit enthält die Schwingungsgleichung nur positive Terme:

$G(s)=\left.{\frac {1}{[s+(\delta -j\omega )]\cdot [s+(\delta +j\omega )]}}={\frac {1}{s^{2}+2\cdot \delta \cdot s+\delta ^{2}+\omega ^{2}}}\ {\mathrel {\hat {=}}}\ {\frac {1}{s^{2}+p\cdot s+q}}\qquad \right|\ p=2\cdot \delta ;\quad q=\delta ^{2}+\omega ^{2}$

Bei negativen Werten der Pole und Nullstellen kann die Übertragungsfunktion algebraisch mit $T=1/s_{p}$ beziehungsweise $T_{v}=1/s_{n}$ in die Zeitkonstanten-Darstellung umgerechnet werden:

Beispiel der allgemeinen Form der Zeitkonstantendarstellung mit reellen Linearfaktoren:

Die Zeitkonstanten-Darstellung errechnet sich direkt aus der Pol-Nullstellendarstellung, indem der Produktterm so umgeformt wird, dass beide Formen mathematisch identisch sind: Der Produktterm s - s_n wird so umgestellt, dass der Reziprokwert 1/s_n = T gebildet wird. Die Variable a entspricht der Nullstelle oder der Polstelle mit negativem Realteil.

Der Produktterm in der Zeitkonstanten-Darstellung mit negativem Wert der Polstelle s_P (Term im Nenner asymptotisch stabiles System) lautet damit:

$\underbrace {(s-s_{p})} _{\text{Produktterm}}\ :=\underbrace {(s+a)} _{\text{Produktterm}}=\ \underbrace {a\cdot ({\frac {1}{a}}\cdot s+1)} _{a={\text{negativer Wert}}}\quad :=\underbrace {K\cdot (T\cdot s+1)} _{\text{Zeitkonstantendarstellung}}$.

Bei der Zeitkonstantendarstellung des Linearfaktors werden die Terme positiv dargestellt. Dies setzt voraus, dass die Realanteile der zugehörigen Nullstellen und Pole negativ sind.

$G(s)={\frac {K\cdot (T_{V1}\cdot s+1)(T_{V2}\cdot s+1)\dotsm (T_{Vm}\cdot s+1)}{(T_{1}\cdot s+1)(T_{2}\cdot s+1)\dotsm (T_{n}\cdot s+1)}}$

Dieses Gesamtsystem wird für n > m (Anzahl der differenzierenden Elemente ist kleiner als die Anzahl der verzögernden Elemente) als "globales proportionales Systemverhalten" bezeichnet.

Es wird aus der Systemtheorie der Analyse der Übertragungsfunktion gezeigt, dass nur drei verschiedene nicht mehr zerlegbare Polynom-Produkte entstehen, die ein unterschiedliches Verhalten haben, ob sie im Nenner oder Zähler der Übertragungsfunktion stehen. Alle Übertragungsfunktionen G(s) höherer Ordnung setzen sich aus diesen drei unterschiedlichen Polynomprodukten zusammen. Bereits aus den zwei Linearfaktoren 1. Ordnung vom Typ $G_{1}(s)$ und $G_{2}(s)$, jeweils im Zähler oder im Nenner stehend, lassen sich sämtliche phasenminimale lineare Übertragungssysteme oder verschachtelte Übertragungsfunktionen oder Regelsysteme mit Rückführungen nachbilden, auch $PT2_{kk}$-Schwingungsglieder durch einen Hilfsregelkreis mit $PT1$-Glied und $I$-Glied.

Linearfaktoren in der Zeitkonstantendarstellung:

Typ Linearfaktor	Bedeutung im Zähler	Bedeutung im Nenner
$G_{1}(s)=T\cdot s$	Differenzierer, D-Glied	Integrator, I-Glied
$G_{2}(s)=T\cdot s+1$	Proportionales Differentiales-Glied; PD1-Glied	Verzögerung, PT1-Glied
$G_{3}(s)=T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1$ (besteht aus 2 Linearfaktoren)	PD2-Glied: für 0 < D < 1 mit konjugiert komplexen Nullstellen	Schwingungsglied PT2-Glied: für 0 < D < 1 mit konjugiert komplexen Polen

Die Berechnung der Ausgangsgröße y(t) einer gegebenen Übertragungsfunktion G(s) und gegebenen Eingangssignal U(s) erfolgt über die inverse Laplace-Transformation.

Für y(t) lautet der Suchbegriff für die inverse Transformation in der Laplace-Transformationstabelle für den Zeitbereich:

$y(t)={\mathcal {L}}^{-1}\underbrace {\left\{G(s)\cdot U(s)\right\}} _{\text{Suchbegriff}}$

Verstärkungsfaktoren K einzelner Teilsysteme im s-Bereich haben kein Zeitverhalten und können zusammengefasst werden.

Lineare dynamische Systeme können aus folgenden 6 verschiedenen Teilsystemen G(s) bestehen:

I-Glied	D-Glied	PT1-Glied,	PD1-Glied	PT2kk-Glied	PD2kk-Glied
${\frac {Y}{U}}(s)={\frac {1}{T_{I}\cdot s}}$	${\frac {Y}{U}}(s)=T_{v}\cdot s$	${\frac {Y}{U}}(s)={\frac {1}{T_{1}\cdot s+1}}$	${\frac {Y}{U}}(s)=T_{v}\cdot s+1$	${\frac {Y}{U}}(s)={\frac {1}{T_{1}^{2}\cdot s^{2}+2\cdot D\cdot T_{1}\cdot s+1}}$	${\frac {Y}{U}}(s)=T_{v}^{2}\cdot s^{2}+2\cdot D\cdot T_{v}\cdot s+1$

Die dargestellten Systeme mit differenzierender Wirkung, wie das $PD1$-Glied, $D$-Glied und $PD2_{kk}$-Glied, sind ideale Übertragungsglieder, die technisch so nicht realisierbar sind. Für eine Simulation am Computer lässt sich aber mit den idealen differenzierenden Übertragungssystemen vortrefflich rechnen.

Das Modell eines beliebigen Übertragungssystems wird üblicherweise zum besseren Verständnis in Funktionsblöcken dargestellt. In Reihe geschaltete Teilsysteme in Blockstruktur wirken multiplikativ, parallelgeschaltete Teilsysteme additiv. Wird das Ausgangssignal eines Teilsystems in den Eingang des von links nach rechts angeordneten nächsten Teilsystems gegeben und das Ausgangssignal der Systemkette auf den System-Eingang zurückgeführt, handelt es sich um eine Kreisschaltung mit positiver (nichtphasenminimale) oder negativer (phasenminimale) Rückkopplung.

Für die numerische Berechnung der dargestellten Übertragungsglieder G(s) des s-Bereiches in den Zeitbereich werden Differenzengleichungen verwendet, die aus den Differenzialgleichungen der zugehörigen Übertragungsfunktionen entwickelt werden.

Fazit:

Es existieren nur 3 Formen von Linearfaktoren - jeweils im Zähler und Nenner der Übertragungsfunktion - also 6 Formen von Elementarsystemen oder deren Vielfache in einem linearen dynamischen System. Gleiche Formen von Linearfaktoren mit gleichen Zeitkonstanten im Zähler und Nenner der Übertragungsfunktion G(s) stehend, kompensieren sich vollständig zu 1.

Das gilt auch für die Anwendung diesen Linearfaktoren zugehörigen Differenzengleichungen zur Berechnung der Ausgangsgröße für ein Zeitintervall im diskreten Zeitbereich bei gegebener Eingangsgröße. In diesem Fall existieren je drei Formen von Differenzengleichungen mit verzögerndem oder differenzierendem Systemverhalten. Die Differenzengleichung mit differenzierendem und verzögerndem Verhalten bei gleichen Zeitkonstanten kompensieren sich vollständig.

Einführung Differenzengleichungen

Differenzengleichungen der einfachsten Art beziehen sich auf die Differenzialgleichungen der Linearfaktoren G(s) erster Ordnung, deren Differentialquotienten durch Differenzenquotienten ersetzt wurden. Das Ergebnis der Ausgangsgröße eines Systems für eine gegebene Eingangsgröße wird rekursiv für die Folgen $k=(0,1,2,3,\cdots k_{MAX})$ im zeitlichen Abstand $\Delta t$ berechnet. Die kontinuierlichen mathematischen Operationen der Integration und Differentiation werden zeitdiskret durch Summen- und Differenzenbildung angenähert.

Je nach Anwendung des expliziten oder impliziten Eulerverfahrens erfolgt die Approximation (Annäherung) an die Integrationsfunktion schrittweise durch einen über Differenzengleichungen errechneten Wert zwischen zwei Rekursionsfolgen k-1 zu k oder k+1 zu k.

Meistens wird zur Aufstellung der Differenzengleichungen das explizite Euler-Rückwärtsverfahren verwendet. Nach diesem Verfahren können aus den zugehörigen Differenzialgleichungen der 4 Elementarsysteme G(s) erster Ordnung der Übertragungsfunktionen Differenzengleichungen gebildet werden, indem an Stelle des Differenzialquotienten mit $dy/dt$ der Differenzenquotient ${\frac {\Delta y}{\Delta t}}={\frac {y_{(k)}-y_{(k-1)}}{\Delta t}}$ näherungsweise eingeführt wird.

Die Differenzengleichungen beschreiben mit dem Approximationsalgorithmus für ein kleines Zeitintervall ∆t die Signaländerungen nach jedem Zeitintervall als Funktion des betreffenden Teilsystems (Linearfaktoren) und des Eingangssignals. Mit der fortlaufenden Wiederholung der Berechnung mit dem Zeitintervalls ∆t und Addition der Änderungsergebnisse $f(u_{(k)};\Delta t;T)$ ergibt sich der Signalverlauf eines Systems über die Zeit $k_{MAX}\cdot \Delta t$.

Für eine Berechnung des Ausgangssignals y(t) eines dynamischen Systems mit Differenzengleichungen werden die Linearfaktoren ersten Grades der Übertragungsfunktion G(s) berücksichtigt. Jede Berechnung einer Differenzengleichung ist die Lösung im Zeitbereich für ein Zeitintervall $\Delta t$.

Beispiel für ein Verzögerungsglied:

$y_{(k)}=f(y_{(k-1)};u_{(k)};\Delta t;T)$

Jede aktuelle Berechnungsfolge $y_{(k)}$ bezieht sich auf das vorhergehende Ergebnis $y_{(k-1)}$ und addiert die Änderung des Eingangssignals u_(k) unter Berücksichtigung der Zeitkonstante T und des Zeitintervalls $\Delta t$.

Verzögerungssysteme zweiter Ordnung mit konjugiert komplexen Poilen (im Nenner der Übertragungsfunktion = PT2_KK-Glied, Schwingungsglied) können durch einen einfachen Hilfsregelkreis mit der Reihenschaltung eines I-Gliedes und eines PT1-Gliedes und der negativen Rückführung nachgebildet werden. Für die Nachbildung mit diesen beiden Elementarsystemen sind die zugehörigen Differenzengleichungen erforderlich.

Instabile nicht phasenminimale elementare Übertragungsfunktionen enthalten ein negatives Zeichen in der Übertragungsfunktion und in der zugehörigen Differenzengleichung.

Die Genauigkeit der numerischen Berechnung eines dynamischen Systems mit dem Euler-Verfahren steigt linear mit dem kleiner werdenden Zeitintervall ∆t.

Der numerische Berechnungsalgorithmus nach dem Euler-Rückwärts-Verfahren ist in den nachfolgen Kapiteln mit der Tabelle "Tabellarische Darstellung der Differenzengleichungen" aufgestellt.

Theorie der Rechteckapproximation des Eulerverfahrens

Eulerverfahren

Definition der Obersumme und Untersumme der numerischen Integration.

Die einfachste Methode ist die Rechteckapproximation mit dem Zeitintervall ∆t (Integrationsintervall) an eine analytische Funktion f(t).

Die numerische Integration einer monoton steigenden analytischen Funktion für ein Zeitintervall entspricht der Fläche des berechneten Ausgangssignals y_(k) einer beliebigen Folge für die Zeit Δt, also y_(k) * Δt. Je nach verwendetem Verfahren der numerischen Annäherung an die rechte oder linke Intervallgrenze der Folge k-1, k, k+1 spricht man von der Annäherung als Obersumme oder Untersumme der Integration.

Die Funktion einer einfachen Integration wird durch die Summe der Folgen des Produktes u_(k) * ∆t nachgebildet:

$y(t)={\frac {1}{T_{I}}}\cdot \int u(t)\cdot dt\quad \rightarrow \quad y_{(k)}={\frac {1}{T_{I}}}\cdot \sum _{i}u_{(i\cdot \Delta t)}\cdot \Delta t$

Bei der numerischen Berechnung der Sprungantwort der Integrations-Funktion zur Annäherung an die analytische Funktion f(t) wird als Treppenkurve dargestellt. Es wird unterschieden, ob die Rechteck-Annäherung mit der rechten oder linken Intervallgrenze erfolgt und sich als Obersumme oder Untersumme zeigt.

Explizites Eulerverfahren

Das einfachste numerische Verfahren der Berechnung des Ausgangssignals $y(t)$ eines linearen Übertragungssystems als Funktion des Eingangssignals $u(t)$ ist das sogenannte explizite Eulerverfahren (auch Euler-Vorwärtsverfahren, Streckenzugverfahren, Rechteckverfahren, Tangentenverfahren genannt), bei dem durch wiederholte Berechnungen für eine kleines Zeitintervall $\Delta t$ eine Annäherung an die analytische Funktion des Systems durchgeführt wird.

Diese Annäherung bezieht sich auf die linke Seite des Streckenzuges der (Rechteckapproximation) und liegt unterhalb einer ansteigenden Originalfunktion. Deshalb wird diese Annäherung auch mit Untersumme bezeichnet.

$y_{(k+1)}=y_{(k)}+\Delta t\cdot f[y_{(k)},u_{(k)}]$

Implizites Eulerverfahren

Alternativ kann das Eulerverfahren (Euler-Rückwärts) auch an der rechten Seite des Streckenzuges am Ende des Integrationsintervalls definiert werden.

$y_{(k+1)}=y_{(k)}+\Delta t\cdot f[y_{(k+1)},u_{(k+1)}]$

Diese Anwendung führt zu dem implizierten Euler-Verfahren, weil der nicht bekannte Wert y_(k+1) auch in der rechten Seite der Gleichung steht. Nur in sehr einfachen Fällen kann diese Gleichung in eine explizite Gleichung überführt werden. Die Anwendung des Verfahrens führt zu einer Annäherung oberhalb der Originalfunktion und wird deshalb mit Obersumme bezeichnet.

Das implizite Euler-Verfahren gilt als das genauere, rechenintensivere aber auch als numerisch stabilere Verfahren.

Modifiziertes explizites Euler-Rückwärtsverfahren

Ein modifiziertes explizites Euler-Rückwärts-Verfahren als Integrationsalgorithmus bezieht sich auf die Zurücksetzung der Integrationsgrenzen des implizierten Euler-Verfahrens des Streckenzuges k und k+1 um (-1). Die Annäherung an die Originalfunktion wirkt als Obersumme.

Damit lautet die Annäherung des Differenzen-Quotienten an den Differential-Quotient:

${\frac {dy}{dt}}=\lim _{\Delta t\,\to \,0}\underbrace {\frac {y_{(k)}-y_{(k-1)}}{\Delta t}} _{Differenzenquotient}$

Der Wert für $\Delta t$ wird in der Praxis wie folgt gewählt:

• $\Delta t$ << als die dominante Zeitkonstante des dynamischen Systems, zum Beispiel 1 % oder noch kleiner.
• $\Delta t$ < als die kleinste System-Zeitkonstante, anderenfalls entstehen Fehler.

Beispielsweise lautet der Integrationsalgorithmus:

$y_{(k)}=y_{(k-1)}+\Delta t\cdot f[u_{(k)}]$

Die nachfolgenden Definitionen der Differenzengleichungen beziehen sich auf diese Form. Der Vorteil:

• leichteres Verständnis der numerischen Integration. Sie bezieht sich auf eine Folge der Addition einer zurückliegenden Berechnung $y_{(k-1)}$ und einem aktuellen additiven Anteil als Funktion:

$f[{\text{Übertragungsglied}};u_{(k)};\Delta t]$.

• Teilsysteme mit gleichen Polen und Nullstellen kompensieren sich.

Zum Zeitpunkt t = 0 = k₍₀₎ * Δt hat eine Funktion 1. Ordnung beispielsweise ein Verzögerungsglied einen Anfangswert proportional u_(k), der differenzierbar ist. Damit kann in einer Reihenschaltung von Teilsystemen 1. Ordnung mit verzögerndem und differenzierendem Verhalten bei gleichen Polen und Nullstellen innerhalb der Berechnung jeder Folge k eine vollständige Systemkompensation stattfinden. So kompensieren sich die Ergebnisse der Differenzengleichungen eines PT1-Gliedes mit dem eines PD1-Gliedes bei gleichen Zeitkonstanten vollständig.

Ableitung der Differenzengleichungen erster Ordnung nach dem modifizierten Euler-Rückwärtsverfahren

Differenzengleichung der Integration (I-Glied)

Die Übertragungsfunktion lautet:

$\ G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{T_{I}\cdot s}}$

Die zugehörige Differenzialgleichung lautet:

$T_{I}\cdot {\dot {y}}(t)=u(t)$

Der Differenzenquotient wird an Stelle des Differenzialquotienten ${\dot {y}}(t)$ eingesetzt:

$T_{I}\cdot {\frac {y_{(k)}-y_{(k-1)}}{\Delta t}}=u_{(k)}$

Damit lautet die nach $y_{(k)}$ umgestellte Differenzengleichung des I-Gliedes:

$y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T_{I}}}$

Differenzengleichung des Differenzierers (ideales D-Glied)

Mit der Zeitdiskretisierung wird der Übergang einer Differenzialgleichung in eine Differenzengleichung von einer zeitkontinuierlichen Systembeschreibung in eine Systembeschreibung mit kleinen Zeitintervallen Δt der diskreten Zeit geschaffen. Der Differentialquotient wird durch einen Differenzenquotient ersetzt.

Die Übertragungsfunktion des idealen Differenzierers lautet:

$G(s)={\frac {Y(s)}{U(s)}}=T_{V}\cdot s$

Differenzialgleichung des idealen Differenzierers:

$y(t)=T_{V}\cdot {\frac {d}{dt}}{u(t)}$

Der Differenzialquotient ${\dot {u}}(t)$ wird durch einen Differenzenquotient mit der Anpassung an die linke Intervallgrenze ersetzt. Für eine Anpassung an die rechte Intervallgrenze steht der Wert u_(k+1) nicht zur Verfügung.

${\dot {u}}(t)={\frac {du}{dt}}\approx {\frac {\Delta u}{\Delta t}}={\frac {u_{(k)}-u_{(k-1)}}{\Delta t}}$

Differenzengleichung der Differentiation (Ideales D-Glied)

$y_{(k)}=(u_{(k)}-u_{(k-1)})\cdot {\frac {T_{V}}{\Delta t}}$

Differenzengleichung der Verzögerung (PT1-Glied)

Rechteck-Approximation eines PT1-Gliedes durch Berechnung mit einer Differenzengleichung.

Übertragungsfunktion des PT1-Gliedes

$G(s)={\frac {Y(s)}{U(s)}}={\frac {K_{PT}}{1+s\cdot T_{1}}}={\frac {\frac {K_{PT}}{T_{1}}}{s+{\frac {1}{T_{1}}}}}$

Zugehörige Differenzialgleichung

${\dot {y}}(t)+{\frac {1}{T_{1}}}\cdot y(t)={\frac {K_{PT}}{T_{1}}}\cdot u(t)$

Der Differenzialquotient der Differenzialgleichung wird durch den Differenzenquotient ersetzt mit folgendem Ansatz:

${\frac {y_{(k)}-y_{(k-1)}}{\Delta t}}+{\frac {1}{T_{1}}}\cdot y_{(k)}={\frac {K_{PT}}{T_{1}}}\cdot u_{(k)}$

Diese Gleichung wird nach y_(k) aufgelöst.

$y_{(k)}+{\frac {\Delta t}{T_{1}}}\cdot y_{(k)}=y_{(k-1)}+{\frac {K_{PT}\cdot \Delta t}{T_{1}}}\cdot u_{(k)}$

Die Differenzengleichung des PT1-Gliedes lautet:

$y_{(k)}={\frac {T_{1}}{T_{1}+\Delta t}}\cdot y_{(k-1)}+{\frac {\Delta t\cdot K_{PT}}{T_{1}+\Delta t}}\cdot u_{(k)}$

Differenzengleichung des PT1-Gliedes in vereinfachter Schreibweise mit identischer mathematischer Funktion:

$y_{(k)}=y_{(k-1)}+(K_{PT}\cdot u_{(k)}-y_{(k-1)})\cdot {\frac {\Delta t}{T_{1}+\Delta t}}$

Differenzengleichung der Proportional-Differenzialfunktion (Ideales PD1-Glied)

Übertragungsfunktion PD1-Glied:

$G(s)={\frac {Y(s)}{U(s)}}=K_{PD}\cdot (T_{V}\cdot s+1)$

Die zugehörige Differenzialgleichung lautet:

$y(t)=K_{PD}\cdot T_{V}\cdot {\dot {u}}(t)+K_{PD}\cdot u(t)$

Der Differenzialquotient der Differenzialgleichung wird ersetzt durch den Differenzialalgorithmus mit folgendem Ansatz:

$y_{(k)}=K_{PD}\cdot T_{V}\cdot {\frac {u_{(k)}-u_{(k-1)}}{\Delta t}}+K_{PD}\cdot u_{(k)}$

Die Differenzengleichung des idealen PD1-Gliedes lautet:

$y_{(k)}=K_{PD}\cdot [u_{(k)}+(u_{(k)}-u_{(k-1)})\cdot {\frac {T_{V}}{\Delta t}}]$

Anmerkung: Differenzierende Systeme ohne sogenannte parasitäre Zeitkonstanten von PT1-Gliedern lassen sich als Hardware technisch nicht herstellen. Die parasitäre Zeitkonstante ist wesentlich kleiner als die Zeitkonstante des Differenzierers. Dennoch kann man numerisch mit idealen Differenzierern rechnen, dabei ist die Größe des Impulses der Sprungantwort umgekehrt proportional der Größe von Δt. Erst bei der energetischen Bereitstellung der Stellgröße des Reglers aus Zahlenwerten ergibt sich durch die nachgeschaltete Hardware eine unvermeidbare Zeitverzögerung.

Differenzengleichungen höherer Ordnung

Differenzengleichungen können auch aus gewöhnlichen Differenzialgleichungen höherer Ordnung entwickelt werden, wenn ab dem Zeitpunkt $t=kT_{A}\geq 0$ die letzten vergangenen Ausgangs-Wertefolgen mit $k=[-1\to -n]$ und die Eingangs-Wertefolgen mit $k=[-1\to -m]$ bekannt sind.

Zeitkontinuierliche lineare Systeme werden im Zeitbereich durch die gewöhnlichen Differenzialgleichungen n-ter Ordnung mit konstanten Koeffizienten für $n\geq m$ beschrieben. Dabei sind n und m die höchsten Ableitungen der Ausgangssignale $y(t)$ und Eingangssignale $u(t)$.

Eine gegebene gewöhnliche Differentialgleichung wird durch den Koeffizienten $a_{0}$ dividiert, um $y(t)$ freistellen zu können. Diese Form der Differentialgleichung wird entsprechend der dargestellten Koeffizienten wie folgt neu geordnet.

$y(t)+a_{1}{\dot {y}}(t)+a_{2}{\ddot {y}}(t)+\dots +a_{n}y^{(n)}(t)=b_{0}u(t)+b_{1}{\dot {u}}(t)+b_{2}{\ddot {u}}(t)+\dots +b_{m}u^{(m)}(t)$.

Diese Differentialgleichung kann in eine Differenzengleichung überführt werden:

• Es wird $\Delta t=T_{A}$ als Abtastzeit gesetzt, wie in der digitalen Regelung üblich.
• $f(kT_{A})$ wird vereinfacht als $f_{(k)}$ geschrieben und entspricht einem aktuellen Folgeglied.
• Die kontinuierlichen Systemgrößen $y(t)\to y_{(k)}$ und $u(t)\to u_{(k)}$ werden zeitdiskret dargestellt.
• Die Ableitungen im Zeitbereich $dy/dt$ werden entsprechend der Ordnung durch Differenzenquotienten $\Delta y/\Delta t$ der zugehörigen Ordnung ersetzt.

Jede Ableitung der Systemgrößen wird im zeitdiskreten Bereich entsprechend der Ordnung als zurückliegende Folgeglieder der Eingangs- und Ausgangsfolgen k-1 bis k-n oder k-m berücksichtigt.

Daraus folgt die Differenzengleichung:

$y_{(k)}+a_{1}\cdot y_{(k-1)}+a_{2}\cdot y_{(k-2)}+\dots +a_{n}\cdot y_{(k-n)}=b_{0}\cdot u_{(k)}+b_{1}\cdot u_{(k-1)}+b_{2}\cdot u_{(k-2)}+\dots +b_{m}\cdot u_{(k-m)}$.

Damit kann die allgemeine Form der Differenzengleichung nach $y_{(k)}$ aufgelöst werden:

$y_{(k)}=b_{0}\cdot u_{(k)}+b_{1}\cdot u_{(k-1)}+b_{2}\cdot u_{(k-2)}+\dots +b_{m}\cdot u_{(k-m)}-a_{1}\cdot y_{(k-1)}-a_{2}\cdot y_{(k-2)}-\dots -a_{n}\cdot y_{(k-n)}$.

Für die numerische Berechnung eines dynamischen Systems wird die Übertragungsfunktion $G(s)$ oder die zugehörige Differentialgleichung benötigt. Die Umsetzung einer systembeschreibenden Differentialgleichung in eine angenäherte Differenzengleichung zur Beschreibung von Eingangsfolgen und Ausgangsfolgen eines dynamischen Systems wird ermöglicht, wenn die Differentiale der Differentialgleichung durch Rückwärts-Differenzenquotienten über die Abtastperiode ersetzt werden.

Die folgenden Ableitungen der Differentialquotienten in Differenzenquotienten der 1. 2. und 3. Ordnung sind gegeben:

Differenzenquotient 1. Ordnung:

${\dot {y}}(t)={\frac {dy}{dt}}\approx {\frac {\Delta y}{\Delta t}}={\frac {\Delta y_{k}}{T_{A}}}={\frac {y_{(k)}-y_{(k-1)}}{T_{A}}}$

Der Differenzenquotient 2. Ordnung entsteht aus Differenzen der Differenz:

${\ddot {y}}(t)={\frac {d^{2}y}{dt^{2}}}\approx {\frac {\Delta ^{2}y_{k}}{T_{A}^{2}}}={\frac {y_{(k)}-2y_{(k-1)}+y_{(k-2)}}{T_{A}^{2}}}$

Der Differenzenquotient 3. Ordnung lautet:

$y^{(3)}(t)={\frac {d^{3}y}{dt^{3}}}\approx {\frac {\Delta ^{3}y_{k}}{T_{A}^{3}}}={\frac {y_{(k)}-3y_{(k-1)}+3y_{(k-2)}-y_{(k-3)}}{T_{A}^{3}}}$

Nach erfolgtem Einsetzen der Differenzenquotienten in die Differenzengleichung eines dynamischen Systems lassen sich die neuen Koeffizienten aus den Koeffizienten der Differentialgleichung berechnen.

Beispiel der Entwicklung einer Differenzengleichung zur Berechnung der Sprungantwort eines $PT2_{kk}$-Gliedes mit konjugiert komplexen Polen:

Sprungantwort eines PT2-Gliedes mit konjugiert komplexen Polen. Δt = 0,01 sec.
$0{,}25{\ddot {y}}(t)+0{,}125{\dot {y}}(t)+y(t)=1(t)$

Gegeben: Übertragungsfunktion im s-Bereich: $G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{0{,}25s^{2}+0{,}125s+1}}$ Sprungfunktion: u(t)=1 Gesucht: Differenzengleichung $y_{(k)}$ zur numerischen Bestimmung des System-Zeitverhaltens. Zugehörige Differentialgleichung nach dem Differentiationssatz der Laplace-Transformation: $0{,}25{\ddot {y}}(t)+0{,}125{\dot {y}}(t)+y(t)=u(t)$ Die Differenzenquotienten für ${\ddot {y}}(t)$ und ${\dot {y}}(t)$ werden in die nachfolgende Differenzengleichung eingesetzt: $0{,}25\cdot {\frac {y_{(k)}-2y_{(k-1)}+y_{(k-2)}}{T_{A}^{2}}}+0{,}125\cdot {\frac {y_{(k)}-y_{(k-1)}}{T_{A}}}+y_{k}=u_{k}\quad |\qquad y(t)\to y_{(k)};\ u(t)\to u_{(k)}$ Die Brüche werden in einzelne additive Terme aufgelöst, um $y_{(k)}$ freistellen zu können: $y_{(k)}{\bigg (}{\frac {0{,}25}{T_{A}^{2}}}+{\frac {0{,}125}{T_{A}}}+1{\bigg )}=u_{(k)}+{\frac {0{,}5y_{(k-1)}}{T_{A}^{2}}}-{\frac {0{,}25y_{(k-2)}}{T_{A}^{2}}}+{\frac {0{,}125y_{(k-1)}}{T_{A}}}$ $y_{(k)}={\frac {u_{(k)}}{\lambda }}+{\frac {0{,}5y_{(k-1)}}{\lambda T_{A}^{2}}}-{\frac {0{,}25y_{(k-2)}}{\lambda T_{A}^{2}}}+{\frac {0{,}125y_{(k-1)}}{\lambda T_{A}}}\quad {\bigg |}\qquad \lambda ={\frac {0{,}25}{T_{A}^{2}}}+{\frac {0{,}125}{T_{A}}}+1;\quad u_{(k)}=1$ Berechnungsbeispiel für einige Werte der Ausgangsfolge $y_{(k)}$ mit $T_{A}=0{,}01;\quad \lambda =2513{,}5;\quad u_{(k)}=1$: $y_{(k=0)}=0{,}0004+0-0+0=0{,}0004$. $y_{(k=1)}=0{,}0004+0{,}0008-0+0=0{,}0012$. $y_{(k=2)}=0{,}0004+0{,}0024-0{,}0004+0=0{,}0024$. $y_{(k=157)}=0{,}0004+3{,}286-1{,}643+0{,}008=1{,}652$.

Diese Differenzengleichung entspricht einem Rekursionsalgorithmus eines dynamischen Systems, der schrittweise mit einem digitalen Rechner gelöst werden kann. Aus der Eingangsfolge $u_{(k)}$ berechnet der Rechner synchron zur Abtastung die Ausgangsfolge $y_{(k)}$.

Die rekursive Berechnung der Differenzengleichung 2. Ordnung bezieht sich für die aktuelle Ausgangsfolge $y_{(k)}$ durch Einsetzen der zurückliegenden Werte der Ausgangsfolge $u_{(k-1)}$ und $u_{(k-2)}$ in die Gleichung. Für das 1. Folgeglied der Berechnungsfolge k=0 sind die zurückliegenden Werte der Ausgangsfolge noch nicht verfügbar und damit Null. Die Anzahl $k=(0,1,2,3,\dots k_{\mathrm {max} })$ der Glieder der Ausgangsfolge wird durch die diskrete Zeit $T_{A}$ und durch die gewünschte zu beobachtende Gesamtzeit des Einschwingvorgangs bestimmt.

Als Offline-Berechnung mit $\Delta t=0{,}01$ [s] und einer Beobachtungszeit von 24 [s] wird die diese Gleichung 2400-mal berechnet und ergibt damit 2400 Folgewerte, die zur grafischen Darstellung gespeichert werden. Gegenüber der analytischen Funktion ist mit einem Approximationsfehler um ca. 1 % zu rechnen.

Zusammenfassung der Berechnung mit Differenzengleichungen

• Euler-Rechteck-Verfahren

Durch unterschiedliche Verfahren der Approximation (Annäherung) an eine zeitabhängige Funktion wie zum Beispiel für ein Verzögerungsglied 1. Ordnung existieren unterschiedliche Differenzengleichungen.

Das einfachste Verfahren ist das Euler-Rechteck-Verfahren. Für die genannten vier linearen Teilsysteme wurden aus den zugehörigen DGL Differenzengleichungen abgeleitet.

• Berechnungsfolge

Eine Berechnungsfolge bezieht sich auf das gesamte Übertragungssystem für das Zeitintervall ∆t.

In einer Folge k = (0, 1, 2, 3, … k_MAX) werden beliebig viele Einzelsysteme eines Gesamtsystems hintereinander für ein konstantes Zeitintervall ∆t mittels Differenzengleichungen berechnet.

• Reihendarstellung

Jeder Signalausgang eines Teilsystems ist in der Reihendarstellung der Signaleingang des nächsten Teilsystems (multiplikative Funktion).

• Maximale Folge k_MAX

Der Endwert der Folge k_MAX ergibt sich für den gewünschten Betrachtungszeitraum t_MAX:

$k_{MAX}={\frac {t_{MAX}}{\Delta t}}$ .

• Nichtlineare Systeme

Nichtlineare statische Systeme in Verbindung mit linearen dynamischen Systemen benötigen analytische Gleichungen oder Wertetabellen.

• Tabellarische Anordnung der Differenzengleichungen

Für die Anwendung der Differenzengleichungen empfiehlt sich eine tabellarische Anordnung der Gleichungen, indem entsprechend einem Blockdiagramm der Signalflüsse beginnend von einer Spalte $k\cdot \Delta t$ von links nach rechts die multiplikativen Zusammenhänge der Teilsysteme in den Zellen einer Zeile stehen.

Damit steht in der ersten Spalte der absolute Zeitmaßstab $k\cdot \Delta t$ , in der 2. Spalte die Eingangsgröße (das zeitdiskrete Testsignal) und für alle weiteren Zellen der Spalten der gleichen Zeile die Differenzengleichungen, für die jeweils jede Berechnungsfolge mit $k\cdot \Delta t$ durchgeführt wird.

Es können auch unstetige sprungartige Eingangssignale als Wertetabelle in die 2. Spalte eingetragen werden.

• PT2-Glieder mit konjugiert komplexen Polen können durch Differenzengleichungen mit Differenzenquotienten 2. Ordnung oder durch einen unterlagerten Regelkreis mit einem PT1-Glied und einem I-Glied nachgebildet werden.

• PD2-Glieder mit konjugiert komplexen Nullstellen

Sie entstehen durch Produktbildung zweier PD1-Glieder und Subtraktion mit einem D-Glied.

Anwendung: Als Vorfilter an einem Regelkreis zur Reduzierung von Schwinganteilen der Ausgangsgröße y_(k).

• Die Differenzengleichung eines nichtregulären (instabilen) PT1-Gliedes G_PT1(s) = 1 / (T*s-1) entsteht durch Vorzeichenumkehr der betreffenden Differenzengleichung.

• Nichtlineares Verhalten einer Signalbegrenzung

Die Signalbegrenzung kann mit einem logischen Operator als WENN-DANN-SONST-Anweisung realisiert werden. Zum Beispiel mit Zelleneintrag einer Spalte: Wenn u_(k) > Bezugswert, dann u_(k) = Bezugswert (positive Begrenzung)

• Nichtlineares Verhalten einer Geräte-Kennlinie erfordert eine Wertetabelle als Tabellenspalte, die der Folge k zugeordnet werden muss. Dies gilt für den Fall, dass eine analytische Gleichung das nichtlinearem Systemverhalten nicht beschreiben kann.

• Totzeitsysteme

Totzeitsysteme lassen sich mit einer Programmschleife beschreiben.

Bei Anwendung der Tabellenkalkulation gilt die Rechenanweisung:

INDEX(F20; F200; 180 - Tt / Δt) und bedeutet: Diese Gleichung steht in der obersten Spalte G200 für k = 0 und k * Δt = 0 und bezieht sich auf die Spalte F20 bis F200. Es dürfen keine Zeichen innerhalb der Zellen 20 bis 200 dieses Spaltenbereichs stehen.

• Numerische Stabilität

Zur Vermeidung der numerischen Instabilität kann die Verstärkung nicht unbegrenzt hoch gewählt werden, wenn es auch theoretisch bei stetig wirkenden Regelkreisen bis zu zwei Verzögerungsgliedern möglich wäre.

Bedingung: Bei sehr großer Kreisverstärkung K einer Regelkreisnachbildung muss $\Delta t$ kleiner als $T_{D}/K$ sein. $K$ ist das Produkt aller Einzelverstärkungen, $T_{D}$ ist die dominante Systemzeitkonstante.

• Genauigkeit der numerischen Simulation

Die Genauigkeit steigt mit kleiner werdendem Zeitintervall $\Delta t$ gegenüber der dominanten Systemzeitkonstante $T_{D}$. Der Approximationsfehler $F_{A}$ im Vergleich zur analytische Funktion beträgt $F_{A}\approx {\frac {\Delta t\cdot 100}{T_{D}}}\ [\%]$.

Das Zeitintervall $\Delta t$ muss kleiner als die kleinste zu berechnende Systemzeitkonstante betragen. Anderenfalls treten zusätzliche Fehler auf.

• Eingangssignale / Testsignale:
  • Das Eingangstestsignal u_(k) eines Übertragungssystems ist eine Funktion von ∆t und bezieht sich meistens auf die Testsignale: Impulsfunktion, Sprungfunktion und Anstiegsfunktion.
  • Normierte Sprungfunktion: u_(k) = 1
  • Normierter δ-Impuls: u_(k=0) = 1 / Δt ; u_{(k > 0)} = 0
  • Anstiegsfunktion: u_(k) = u_(k-1) + c * Δt ; c = Δu / Δt

• Kommerzielle Programme
  • Kommerzielle Programme zu numerischen Berechnungen wie MatLab unterscheiden sich von selbst entwickelten numerischen Berechnungen in drei wesentlichen Punkten:
  • Es kann eine gewünschte Berechnungsgenauigkeit durch ausgewählte Verfahren bestimmt werden.
  • Die gewählten Verfahren sind adaptiv, d.h. es muss keine diskrete Zeit und maximale Folge vorgegeben werden. Die Größe des Zeitintervalls ist auch nicht über alle Folgen konstant.
  • Die gewählten Verfahren kontrollieren die Stabilität der Lösung.

Tabellarische Darstellung der Differenzengleichungen 1. Ordnung

In der folgenden Tabelle sind die Differenzengleichungen der vier elementaren Übertragungssysteme und einige nichtlineare Funktionen und Signale als f(∆t) dargestellt.

Die numerischen Berechnungen mit den Differenzengleichungen können mit jeder Programmiersprache durchgeführt werden. Es empfiehlt sich aber der Einfachheit halber die Anwendung der Tabellenkalkulation, mit der auch die grafische Darstellung des Systemverhaltens für ein beliebiges Testsignal hergestellt werden kann. Programmierfehler anderer Programmiersprachen werden vermieden.

Tabelle der Differenzengleichungen und logischen Operationen für die Simulation von Übertragungssystemen

Typ	Übertragungsfunktionen Definition der Testsignale und Operatoren	Differenzengleichungen, Operatoren als Funktion von k*Δt	Hinweise
1	P-Glied: ${\frac {Y}{U}}(s)=K$	$y_{(k)}=u_{(k)}\cdot K\,$	Die Einzelfaktoren K1, K2 ... der Übertragungsglieder werden sinnvollerweise zu einem Faktor K multipliziert.
2	I-Glied: ${\frac {Y}{U}}(s)={\frac {1}{T\cdot s}}$	$y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T}}$ k = Nummer der Folge Δt = konstante diskretisierte Zeit k * Δt = t = aktuelle Zeit	y(k) = aktueller Ausgangswert u(k) = aktueller Eingangswert y(k-1) = Ausgangswert einer zurückliegenden Folge k = 0: Rechenfolge aller Anfangswerte Normale Anfangswerte sind meist Null
3	PT1-Glied: ${\frac {Y}{U}}(s)={\frac {K_{PT1}}{T\cdot s+1}}$	$y_{(k)}=\,$ $y_{(k-1)}+[K_{PT1}\cdot u_{(k)}-y_{(k-1)}]\cdot {\frac {\Delta t}{T+\Delta t}}$
4	Instabiles PT1-Glied: ${\frac {Y}{U}}(s)={\frac {K_{PT1}}{T\cdot s-1}}$	$y_{(k)}=\,$ $u_{(k-1)}+[K_{PT1}\cdot u_{(k)}+y_{(k-1)}]\cdot {\frac {\Delta t}{T+\Delta t}}$	Pole-Nullstellenkompensation bei instabilen PT1-Gliedern ist nicht erlaubt!
5	D-Glied: ${\frac {Y}{U}}(s)=T\cdot s$	$y_{(k)}=[u_{(k)}-u_{(k-1)}]\cdot {\frac {T}{\Delta t}}$
6	PD1-Glied (Regler): ${\frac {Y}{U}}(s)=K_{PD1}\cdot (T\cdot s+1)$	$y_{(k)}=K_{PD1}\cdot [u_{(k)}+[u_{(k)}-u_{(k-1)}]\cdot {\frac {T}{\Delta t}}]$
7	Totzeitglied: ${\frac {Y}{U}}(s)=K_{T_{t}}\cdot e^{-Tt\cdot s}$	Schleife im Rechenprogramm oder: Anwendung Tabellenkalkulation: INDEX(F20; F200; 180 - Tt / Δt) Maximale Totzeit: $T_{t\ max}=(200-20)\cdot \Delta t\,$ Für KTt ist eine eigene Spalte erforderlich	Tabellenkalkulation: F20;F200 bedeutet Bezug der Spalte F für Zellen F20 bis F200. Sämtliche Gleichungen für INDEX stehen z. B. in der Spalte G ab G200 bis z. B. G1200. In F200 bis F1200 stehen die Eingangswerte bzw. Gleichungen. Spalte F20 bis F200 darf keine Zeichen enthalten, sonst entsteht eine fehlerhafte Zuweisung.
8	Regelabweichung: $E(s)=W(s)-Y(s)\,$	$e_{(k)}=W_{(k)}-Y_{(k-1)}\,$	Regelabweichung = Sollwert – Istwert
9	Symmetrische Signalbegrenzung:	WENN-, DANN-; SONST-Anweisung: WENN(X > A; DANN A; WENN(X < -A; DANN -A; SONST X))	X = Zahlenwert einer Zelle A = Parameter der Begrenzung
10	Nichtlineare Kennlinie: als Funktion der Eingangsgröße, Kontinuierliche Funktion: Nichtkontinuierliche Funktion: zum Beispiel Sprung und Rücksprung als Funktion der Zeit (k*Δt)	Anwendung der Tabellenkalkulation: Zelleneintrag einer Gleichung y(k) = f(k; u(k)) Zelleneintrag einer Tabelle: Allen Zellen einer Spalte muss ein Wert zugewiesen werden: y(k) = f(k*Δt)	Für alle Gleichungen gilt: Gleichungen werden pro Zelle z. B. in Zeile 201 einmal geschrieben und beliebig oft entsprechend der gewünschten Signalauflösung z. B. 1000 mal in der Spalte kopiert.
11	Testsignale: Impulsfunktion ${\hat {u}}_{e\delta }(t)={\frac {1}{\Delta t}}$ U(s) = 1	Amplitude: $u_{(k=0)}={\frac {1}{\Delta t}}\,$ Amplitude: $u_{(k>0)}=0\,$	Normierter Impuls!
12	Testsignal Sprungfunktion: U(s) = 1 / s	Sprungfunktion: $u_{(k)}=1\,$	Normierter Sprung!
13	Testsignal Anstiegsfunktion: U(s) = 1 / s²	Anstieg: $u_{(k)}=u_{(k-1)}+c\cdot \Delta t\,$	Anstiegskonstante c = Δ u / Δ t

Anwendung numerischer Berechnungen

Dynamische Systeme, deren Zeitverhalten in Form einer gewöhnlichen Differenzialgleichung g(t) oder durch die Laplace-transformierte Übertragungsfunktion G(s) beschrieben werden, lassen sich sehr vorteilhaft numerisch mit Differenzengleichungen berechnen. Ein dynamisches System besteht häufig aus einer in Funktionsblöcken dargestellten Reihenschaltung, Parallelschaltung oder Zurückkopplung von Teilsystemen, die durch zugehörige Differenzengleichungen beschrieben werden können. Zur besseren Übersicht werden die Rechenergebnisse der einzelnen Differenzengleichungen tabellarisch dargestellt. Mit jeder neuen Berechnungsfolge k des Gesamtsystems einer Tabellenzeile mit beliebig vielen Teilsystemen wird mit den zugehörigen Differenzengleichungen ein neues Gesamtergebnis y(k) für ein Zeitintervall Δt berechnet.

Dabei wird die These vertreten, die Differenzengleichungen nur für Linearfaktoren der Übertragungsfunktion ersten Grades zu verwenden, weil nur 4 solcher Formen (2 im Nenner und 2 im Zähler der Übertragungsfunktion) existieren. Eine 5. und 6. Form von Übertragungssystemen zweiter Ordnung mit konjugiert komplexen Polen können mit den Linearfaktoren erster Ordnung simuliert werden. Es macht wenig Sinn, z.B. einen PID-Regler mit einer mittels z-Transformation gefundenen Differenzengleichung als eine einzige spezielle Gleichung zu benutzen, während es bei Verwendung mit Differenzengleichungen 1. Ordnung 3 einfache Differenzengleichungen für den P-I- D-Anteil eine völlige tabellarische Systemübersicht auf überprüfbare Richtigkeit gegeben ist.

Die numerische Berechnung allgemein erlaubt die Berechnung verschiedenster Problemstellungen, die mit konventionellen Methoden sehr schwierig oder analytisch gar nicht zu lösen sind, wie:

• Dynamischer Systeme, die sich linear und nichtlinear verhalten.
• Verhalten dynamischer Systeme als Folge logischer Befehle oder Wertetabellen.
• Lösen von Differenzialgleichungen ohne und mit Anfangswerten der Systemspeicher.
• Systeme ohne Zeitverhalten, bei denen z.B. die kleinste Einheit Δu eine Funktion der dimensionslosen Eingangsgröße u ist (Beispiel: Mehrpunktregler, oder kombinierte Mehrpunktregler mit zeitabhängigen Rückführungen).

Die Hauptanwendung der numerischen Berechnung mit Differenzengleichungen bezieht sich auf die Berechnung des Ausgangs- Eingangsverhalten von dynamischen Systemen, die gesteuert oder geregelt werden. Da bestimmte Übertragungssysteme sich nichtlinear verhalten, können mittels der numerischen Behandlung logische Operationen (Z.B. WENN - DANN - SONST- Anweisung) mit den Differenzengleichungen kombiniert werden.

Das Eingangs- Ausgangsverhalten eines Dreipunktreglers mit Schaltkriterien als Funktion der Hysterese und der Totzone lässt sich mit logischen Befehlen numerisch beschreiben und grafisch darstellen.

Sehr nützlich ist die Anwendung der numerischen Behandlung in der Regelungstechnik. Durch die Simulation eines Regelkreises - bestehend aus den hintereinander geschalteten Einzelkomponenten des Reglers und der Regelstrecke mit der Schließbedingung $e_{(k)}=w_{(k)}-y_{(k-1)}$ zu einem Kreis - können die Systemparameter des Reglers für eine gegebene Regelstrecke optimiert und das Verhalten der Regelgröße grafisch dargestellt werden.

Gesamtsystem als gewöhnliche Differenzialgleichung

• Das Modell eines linearen Systems mit n Systemspeichern, dass durch eine gewöhnliche Differenzialgleichung mit konstanten Koeffizienten beschrieben ist, kann durch n-fache numerische Integration berechnet werden.
• Von der höchsten Ableitung der Ausgangsgröße y(t) werden über Integratoren erzeugte n Zustandsvariablen x(t) subtrahiert. Die numerische Berechnung bezieht sich fortlaufend auf ein kleines Zeitintervall.

Dieses numerische Verfahren ist erheblich einfacher als die Lösung einer DGL mit konventionellen Methoden, weil es sich um die Lösung einfacher algebraischer Gleichungen handelt.

• Die numerische Berechnung der Differenzialgleichung erlaubt die homogene Lösung mit Vorgabe der Anfangswerte mit y_(k) = 0 , die partikuläre Lösung ohne Anfangswerte mit y_(k) ≠ 0 und die Gesamtlösung mit Anfangswerten und y_(k) ≠ 0.
• Es sind keine Integrationskonstanten zu berechnen.

Numerische Berechnung von Übertragungssystemen mit linearen und nichtlinearen Teilsystemen

Lineare zeitinvariante Übertragungssysteme werden durch DGL-en und Übertragungsfunktionen beschrieben. Durch Zerlegung der Polynome der Übertragungsfunktion in Linearfaktoren 1. Ordnung mit und ohne Grundglied ergeben sich 4 elementare Übertragungsfunktionen mit den Funktionseigenschaften I-Glied, PT1-Glied, D-Glied und PD1-Glied, mit denen in beliebiger Reihen-, Parallel- und Kreisstruktur sich alle phasenminimale Übertragungsfunktionen nachbilden lassen. Für diese elementaren Teilsysteme lassen sich aus den zugehörigen DGL-en je eine Differenzengleichung bilden. Der Approximationsalgorithmus dieser 4 Differenzengleichungen ist aus den zugehörigen DGL abgeleitet. Von den verschiedenen Verfahren ist die Euler-Rechteckannäherung die einfachste.

Sprungantwort eines Regelkreises mit PI-Regler und Stellgrößenbegrenzung.

Für nichtlineare speicherlose Übertragungssysteme wie Signalbegrenzer, nichtlineare oder gebrochene Kennlinien, Totzeitsysteme und diskontinuierliche Eingangssignale lassen sich analytische Gleichungen oder Wertetabellen finden.

Die numerische Berechnung eines Übertragungssystems von linearen und nichtlinearen Einzelsystemen erfolgt sinnvollerweise in Form einer Tabelle mit den Zeilen der Rekursion der Folge k = 0 bis k = k_MAX untereinander für je einen kleinen Berechnungszeitschritt Δt mit den Spaltenzellen der numerischen Gleichungen.

Da statische Gleichungen wie auch Differenzengleichungen nur einmal in die Zelle einer Spalte eingetragen und dann zum Beispiel für k_MAX = 1000 die Gleichungen 1000-mal kopiert werden, muss eine Wertetabelle je nach gewünschter Auflösung von Hand in die Spalte einer Tabelle eingetragen werden.

Sämtliche Systemgleichungen können mit jeder Programmiersprache berechnet werden. Es wird die Anwendung der Tabellenkalkulation wegen der Einfachheit der Anwendung und der einfachen Möglichkeit der grafischen Darstellung der Berechnungsergebnisse empfohlen.

Berechnungsbeispiel eines Modells aus verschiedenen Teilsystemen bestehenden Übertragungssystems

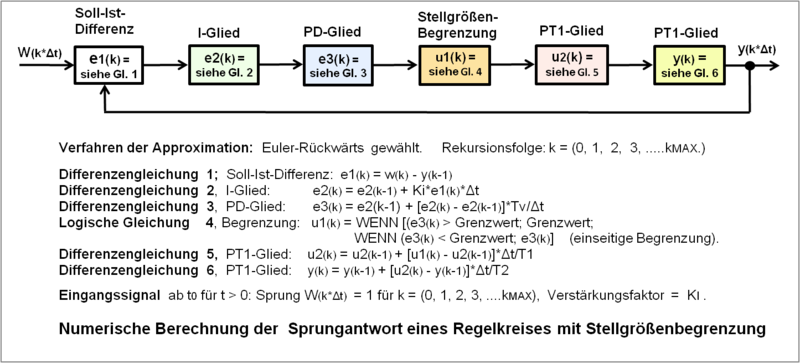
Tabellarische Darstellung der numerischen Gesamtlösung y_(k*Δt) ≈ y(t) eines Regelkreises mit PI-Regler mit Stellgrößenbegrenzung und PT2-Regelstrecke

	Spalte A	Spalte B	Spalte C	Spalte D	Spalte E	Spalte F	Spalte G	Spalte H	Spalte I	Spalte J
	Folge k	Diskr.Zeit Δt	Eing.-Signal u(k)	Soll-Istw. Gl. 1	I-Glied Gl. 2	PD-Glied Gl. 3	Begrenz. Gl. 4	PT1-Glied Gl. 5	PT1-Glied Gl. 6	Bemerkungen
Zeile 1	-	-	-	-	-	-	-	-	-	Kein Eintrag
Zeile 2	0	0*Δt	1	Gl. 1	Gl. 2	Gl. 3	Gl. 4	Gl. 5	Gl. 6	Gleichungen
Zeile 3	1	1*Δt	1	Gl. 1	Gl. 2	Gl. 3	Gl. 4	Gl. 5	Gl. 6	Kopie Zeile 2
Zeile 4	2	2*Δt	1	Gl. 1	Gl. 2	Gl. 3	Gl. 4	Gl. 5	Gl. 6	Kopie Zeile 2
Endzeile	kMAX	kMAX*Δt	1	Gl. 1	Gl. 2	Gl. 3	Gl. 4	Gl. 5	Gl. 6	Kopie Zeile 2

Die Lösung des Systemverhaltens liefert die Spalte I mit der Ausgangsgröße y_(k*Δt).

Nachbildung eines PT2_KK-Schwingungsgliedes

Ein PT2_KK-Schwingungsglied hat konjugiert komplexe Pole und kann deshalb nicht in Linearfaktoren ersten Grades ohne komplexe Anteile von Zahlenwerten zerlegt werden. Für die Bildung der Differenzengleichung eines Übertragungssystems zweiter Ordnung mit konjugiert komplexen Polen kann mit Hilfe eines einfachen Hilfsregelkreises und Anwendung von zwei Differenzengleichungen erster Ordnung erreicht werden.

Berechnung der Koeffizienten eines Hilfsregelkreises aus der Übertragungsfunktion

Die einfachste Form der Nachbildung des Hilfsregelkreis erfolgt durch die offene Hilfsregelstrecke G₀(s) (Indizierung mit H) als Reihenschaltung mit einem I-Glied (K_H / s) mit einem PT1-Glied (1 / (T_H s + 1)). Damit lassen sich zwei Differenzengleichungen für Linearfaktoren erster Ordnung verwenden.

$G_{0}(s)={\frac {Y}{W}}(s)={\frac {K_{H}}{s\cdot (T_{H}\cdot s+1)}}$

Wird der Ausgang Y(s) von G₀(s) in Blocksymbol-Darstellung negativ auf den Systemeingang W(s) zurückgeführt, entsteht der Hilfsregelkreis G(s).

Die Übertragungsfunktion des Hilfsregelkreises G(s) = G₀ / (1+G₀) lautet in der allgemeinen Form für ein PT2_KK-Schwingungsglied:

$G_{H}(s)={\frac {Y}{W}}(s)={\frac {G_{0}}{1+G_{0}}}={\frac {1}{{\frac {T_{H}}{K_{H}}}\cdot s^{2}+{\frac {1}{K_{H}}}\cdot s+1}}\ {\mathrel {\hat {=}}}\ {\frac {1}{T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1}}={\frac {1}{a\cdot s^{2}+b\cdot s+1}}$

Es gilt nun aus der Normalform des Schwingungsgliedes mit gegebenen Zahlenwerten über einen Koeffizientenvergleich die Hilfsgrößen T_H und K_H zu bestimmen, damit die Differenzengleichungen angewendet werden können.

Für eine gegebene Übertragungsfunktion eines Schwingungsgliedes mit den Zahlenwerten der Koeffizienten $a=T^{2}$ und $b=2\cdot D\cdot T$ müssen die Parameter der Verstärkung K_H und der Zeitkonstante T_H des offenen Regelkreises G₀(s) aus dem geschlossenen Hilfsregelkreis G_PT1KK(s) errechnet werden.

Durch Koeffizientenvergleich lassen sich die gewünschten Parameter $K_{H}$ und $T_{H}$ des offenen Hilfsregelkreises bestimmen:

${\frac {T_{H}}{K_{H}}}=a;\qquad {\frac {1}{K_{H}}}=b;\qquad T={\sqrt {a}}$

Mit diesen Parametern kann die numerische Berechnung mit den nachstehend aufgeführten Differenzengleichungen durchgeführt werden.

$T_{H}=a\cdot K_{H}={\frac {a}{b}};\qquad K_{H}={\frac {1}{b}};\qquad {\text{Dämpfung}}\ D={\frac {b}{2\cdot T}}$

Sprungantwort eines PT2_KK-Gliedes,
G(s) = 1 / (0,25 s² + 0,125 s +1)
Dämpfung D = 0,125.

Berechnungsbeispiel:

Gegeben: Übertragungsfunktion eines Schwingungsgliedes $PT2_{KK}$: $G_{PT2KK}={\frac {1}{0,25\cdot s^{2}+0,125\cdot s+1}}={\frac {1}{a\cdot s^{2}+b\cdot s+1}}$ Gesucht: Parameter KH und TH eines offenen Hilfsregelkreises zur Simulation der Übertragungsfunktion des geschlossenen Kreises als ein PT2KK-Schwingungsglied mit konjugiert komplexen Polen. $K_{H}={\frac {1}{b}}={\frac {1}{0,125}}=8$ $T_{H}=a\cdot K_{H}={\frac {a}{b}}={\frac {0,25}{0,125}}=2$ Mit diesen Angaben können die nachstehend aufgeführten Differenzengleichungen berechnet werden.

Numerische Nachbildung des Hilfsregelkreises für ein Schwingungsglied im zeitdiskreten Bereich f(k*Δt)

Der offene Hilfsregelkreis G₀(s) besteht aus der Reihenschaltung eines I-Gliedes mit einem PT₁-Glied. Die Hilfsgrößen wie die Zeitkonstante T_H des PT1-Gliedes und die Verstärkung K_H des I-Gliedes werden in die zugehörigen Differenzengleichungen eingebracht.

Wird die Regelabweichung w_(k) - y_(k-1) in die Reihenschaltung G₀(k) geleitet, ist der Hilfsregelkreis geschlossen. Es müssen folgende drei Differenzengleichungen berechnet werden. w_(k) ist ein Testsignal oder das Ausgangssignal y_(k) eines in der Reihenfolge links liegenden Übertragungsgliedes vor dem Hilfsregelkreis.

Blockschaltbild eines Hilfsregelkreises zur Simulation eines PT2_KK-Schwingungsgliedes.

Systembezeichnung	Differenzengleichung Schwingungsglied
Regelabweichung e(k)	$e_{(k)}=w_{(k)}-y_{(k-1)}$
I-Glied u(k)	$u_{(k)}=u_{(k-1)}+e_{(k)}\cdot K_{H}\cdot \Delta t$
PT1-Glied y(k)	$y_{(k)}=y_{(k-1)}+[u_{(k)}-y_{(k-1)}]\cdot {\frac {\Delta t}{T_{H}+\Delta t}}$

Sollte das zu berechnende Zeitverhalten des Schwingungsgliedes G(s) einen Verstärkungsfaktor K im Zähler der Übertragungsfunktion enthalten, so wird dieser Faktor separat vor oder nach dem Hilfsregelkreis algebraisch $y(k)=K\cdot u(k)$ berücksichtigt.

Numerische Lösung einer systembeschreibenden Differenzialgleichung

Die partikuläre Lösung (Eingangs- Ausgangsverhalten) einer gewöhnlichen DGL mit konstanten Koeffizienten ist abhängig von der Zahl n der Ableitungen der Ausgangsgröße y(t), der Ableitungen der Eingangsgröße u(t), der Größe der Koeffizienten und der Funktion des Eingangssignals u(t). Sie geht von Anfangswerten gleich Null aus. Dabei wird die Differenzialgleichung in die explizite Form nach der höchsten Ableitung umgestellt und grafisch in der Regelungsnormalform der Zustandsraumdarstellung dargestellt.

Sind Anfangswerte der Differenzialgleichung gegeben, werden die Integratoren der Regelungsnormalform auf diese Anfangswerte gesetzt.

Die Differenzialgleichung eines Übertragungssystems in der allgemeinen Form ohne Ableitungen der Eingangsgröße lautet:

$a_{n}\cdot y^{(n)}(t)+\ \cdots \ +a_{2}\cdot {\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)$

Beispiel

Erstellung des Signalflussplanes zur Lösung der DGL 2. Ordnung:

Signalflussplan zur Lösung einer DGL in der expliziten Darstellung. Die Zustandsvariablen x_i ergeben sich durch die Integrationen.

Systembeschreibende DGL $a_{2}\cdot {\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)\,$ Für die numerische Lösung einer gewöhnlichen DGL wird die explizite Form nach der höchsten Ableitung verwendet, d.h. in dem alle Terme der Gleichung durch den Koeffizienten a2 dividiert werden und dann ${\ddot {y}}(t)\,$ freigestellt wird. ${\ddot {y}}(t)={\frac {1}{a_{2}}}\cdot [-a_{0}\cdot y(t)-a_{1}\cdot {\dot {y}}(t)+b_{0}\cdot u(t)]$ Der in dem Strukturbild dargestellte Signalflussplan zeigt anschaulich die Umsetzung der DGL in ein Modell mit Zustandsvariablen xi zur Lösung der DGL.

Dieses Modell entspricht auch der Lösung einer DGL mit Hilfe der Analogrechentechnik und ist seit langem bekannt. Das Interesse galt weniger den dargestellten Zustandsvariablen, sondern nur dem Verhalten der Ausgangsgröße y(t).

Hat die Übertragungsfunktion oder die zugehörige DGL auch differentielle Anteile, d. h. Ableitungen der Eingangsgröße u(t), eignet sich als Signalflussdiagramm der DGL besser die Regelungsnormalform der Zustandsraumdarstellung.

Die numerische Lösung dieser DGL mit n-fachen Ableitungen erfolgt durch n-fache numerische Integrationen, die sich auf ein diskretes Zeitintervall Δt und rekursive Berechnung der Folgen k = (0, 1, 2, 3, ...k_MAX) bezieht.

Die Differenzengleichung zur numerischen Lösung einer Integration lautet (hier T = 1):

$y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T}}$

• Partikuläre Lösung y_P(k):

Für ein gegebenes Eingangssignal u(Δt) zur Zeit k * Δt = 0 und den Anfangswerten der Integratoren y'₀ = 0 und y₀ = 0 ergibt sich eine geschlossene Lösung für y_(k) für k = 0 bis k_MAX.

• Homogene Lösung y_H(k):

Für ein gegebenes Eingangssignal u(Δt) = 0 zur Zeit k * Δt = 0 werden Anfangswerte der Integratoren für y'₀ und y₀ eingesetzt. Es müssen dabei keine Integrationskonstanten C_i ermittelt werden, weil die Integratoren als bestimmte Integrale mit den Integralgrenzen der Anfangswerte bis zum Ende des Betrachtungszeitraumes k * Δt wirken.

• Gesamtlösung y_(k):

Sie ergibt sich automatisch, wenn ein Eingangssignal u(k) ≠ 0 und gleichzeitig Anfangswerte der Integratoren y'₀ ≠ 0 und y₀ ≠ 0 vorliegen.

Berechnungsbeispiel einer gewöhnlichen Differenzialgleichung 2. Ordnung mit Anfangswerten

Sprungantwort eines PT2-Gliedes durch numerische Lösung einer DGL mit System-Anfangswerten.

Übertragungsfunktion gegeben: $G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{(2\cdot s+1)\cdot (s+1)}}$ Zugehörige systembeschreibende DGL in expliziter Darstellung: ${\ddot {y}}(t)=0,5\cdot u(t)-1,5\cdot {\dot {y}}(t)-0,5\cdot y(t)\,$ Anfangswerte der Energiespeicher (Integratoren): y'0(t) = 1; y0(t) = 1; Eingangsgröße u(k) ist eine normierte Sprungfunktion 1 für t > 0. Die zu berechnenden Gleichungen ergeben sich aus dem dargestellten Signalflussplan. In der Tabellendarstellung erfolgt die Berechnung der Zellen einer Zeile von links nach rechts und danach von einer oberen Zeile zu den unteren Zeilen. Benötigte Werte, die an einer bestimmten Stelle einer Zeile noch nicht bekannt sind, werden aus einer vorhergehenden Zeile der gleichen Spalte entnommen. Gleichung 1 bildet die Differenzen der noch zu berechnenden Ableitungen von y(k) in Spalte E der Tabelle laut Signalflussplan: $E2=C2\cdot D2-F1\cdot G2-H1\cdot I2\,$ Gleichung 2 ist eine Differenzengleichung der Integration in Spalte F (mit T = 1): $y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T}}\quad =\quad F2=E1+E2\cdot \Delta t\qquad (T=1)$ Gleichung 3 ist eine Differenzengleichung der Integration in Spalte H (mit T = 1): $y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T}}\quad =\quad H2=F1+F2\cdot \Delta t\qquad (T=1)$ Die Spalte B der diskreten Zeit (k * Δt) berechnet sich ab Zeile B3: B3 = B2 + Δt und kann beliebig oft kopiert werden! Die Lösung der DGL liefert die Spalte H mit der Ausgangsgröße y(k*Δt)!

Tabellarische Darstellung der numerischen Gesamtlösung y_(k*Δt) ≈ y(t) einer Differenzialgleichung 2. Ordnung.

	Spalte A	Spalte B	Spalte C	Spalte D	Spalte E	Spalte F	Spalte G	Spalte H	Spalte I	Spalte J
	Folge k	Zeit Δt	Eingangs Signal	Koeffiz. b0	Differenz Gl. 1	I-Glied Gl. 2	Koeffiz. a1	I-Glied Gl. 3	Koeffiz. a0	Bemerkungen
Zeile 1	-	-	-	-	-	1	-	1	-	Anfangswerte
Zeile 2	0	0*Δt	1	0,5	Gl. 1	Gl. 2	1,5	Gl. 3	0,5	Gleichungen
Zeile 3	1	1*Δt	1	0,5	Gl. 1	Gl. 2	1,5	Gl. 3	0,5	Kopie Zeile 2
Zeile 4	2	2*Δt	1	0,5	Gl. 1	Gl. 2	1,5	Gl. 3	0,5	Kopie Zeile 2
Endzeile	kMAX	kMAX*Δt	1	0,5	Gl. 1	Gl.2	1,5	Gl. 3	0,5	Kopie Zeile 2

Anmerkung:

• Bei der homogenen Lösung sind in Spalte C sämtliche Werte auf 0 gesetzt mit Anfangswerten in Zeile 1.
• Bei der partikulären Lösung sind in Spalte C sämtliche Werte auf 1 gesetzt ohne Anfangswerte in Zeile 1.
• Der Approximationsfehler der Annäherung an die analytische Lösung beträgt ungefähr Δt / T = 0,003 / 2 = 0,0015 = 0,15 %.

Einzelnachweise

Zurück zum Inhaltsverzeichnis