Einführung in die Systemtheorie/ Zeitverhalten elementarer Übertragungsglieder der Übertragungsfunktion

Zeitverhalten elementarer Übertragungsglieder

Systeme mit konzentrierten und verteilten Parametern

Dynamische Systeme ohne räumliche Ausdehnung der Systemspeicher haben konzentrierte Systemparameter. Die System-Ausgangssignale sind nur zeitabhängig.

Dynamische Systeme mit räumlicher Verteilung der Systemspeicher enthalten verteilte Systemparameter. Bei diesen Systemen sind die Variablen nicht nur Funktionen der Zeit sondern auch vom Ort. (Beschreibung durch partielle Differenzialgleichungen)

Die nachfolgenden Systembeschreibungen beziehen sich auf Systeme mit konzentrierten Parametern.

Zeitinvarianz

Ein dynamisches Übertragungssystem ist zeitinvariant, wenn es sich über die Zeit nicht ändert. D.h. die Systemantwort y(t+t₀) auf ein identisches Eingangssignal u(t+t₀) ist von t₀ unabhängig. Die Koeffizienten der mathematischen Systembeschreibung sind konstant (zeitlich unveränderlich, invariant).

Zeitvarianz

Ein zeitvariantes System verhält sich zu verschiedenen Zeitpunkten unterschiedlich. Bei technischen Systemen liegt der Grund dafür meist in zeitabhängigen Parameterwerten, zum Beispiel durch Änderung der Koeffizienten der Energiespeicher [zeitabhängige Koeffizienten der Ableitungen y(t)]. Bei vielen Prozessen sind die Auswirkungen der Zeitvarianz so klein oder langsam, dass diese Systeme näherungsweise als zeitinvariant behandelt werden können.

Beispiel für ein typisches zeitvariantes Verhalten ist eine startende Rakete, deren Masse sich durch den verbrauchten Treibstoff ändert. Häufig spielt bei kleineren Massen der mechanische Verschleiß eine Rolle.

Kausalität

Eine wichtige Eigenschaft dynamischer Systeme ist ihre Kausalität. Sie besagt, dass der Wert der Eingangsgröße zur Zeit t = t₍₀₎ das Verhalten des Systems nur für künftige Zeitpunkte t ≥ t₍₀₎ beeinflussen kann.

Eine Eingangsgröße zum Zeitpunkt t = t₀ kann nur den gegenwärtigen und den zukünftigen Verlauf t ≥ t₀ der Ausgangsgröße beeinflussen.

Ordnung der Übertragungsfunktion

Blockschaltbilder erlauben eine übersichtliche Darstellung von dynamischen Prozessen und deren Signalflüsse.

Die häufigste Darstellungsform für das Eingangs- Ausgangsverhalten eines linearen Übertragungssystems ist die Übertragungsfunktion. Sie ist eine abstrakte nicht messbare mathematische Beschreibung für das Verhalten eines linearen zeitinvarianten Systems im Frequenzbereich mit der komplexen Variable s.

Der mathematische Begriff einer gebrochenen rationalen Funktion ist definiert als Quotient zweier Polynome, wobei die Ordnung des Systems im Nenner höher als im Zähler sein muss. Solche Systeme sind technisch realisierbar und entsprechen dem Eingangs- Ausgangsverhalten eines Übertragungssystems im sogenannten s-Bereich (Bildbereich).

Eine systembeschreibende gewöhnliche Differenzialgleichung kann mit der Laplace-Transformation in eine Übertragungsfunktion zunächst in Polynom-Darstellung als gebrochene rationale Funktion geschrieben werden. Durch Bestimmung der Nullstellen im Zähler und Nenner dieser Funktion kann die Polynomdarstellung in eine Produkt-Darstellung mit Linearfaktoren überführt werden. Ein Linearfaktor ist ein Term, in dem die Variable s nur den Grad 1 hat, d. h. keinen höheren Exponenten als 1 besitzt. Quadratische Linearfaktoren mit konjugiert komplexen Nullstellen haben den Grad 2.

Die Übertragungsfunktion in Polynom-Darstellung wird mit Hilfe der Nullstellenbestimmung nach folgender Gleichung in die Produkt-Darstellung überführt.

Produktdarstellung der Übertragungsfunktion:

$G(s)=K\cdot {\frac {\prod \nolimits _{i=1}^{m}\,(s-s_{0i})}{\prod \nolimits _{i=1}^{n}\,(s-s_{i})}}=K\cdot {\frac {(s-s_{01})(s-s_{02})}{(s-s_{1})(s-s_{2})}}\cdots$

Sind die Werte der Nullstellen bzw. der Pole der Linearfaktoren negativ, dann sind die Produktterme positiv und das System ist stabil. Systeme mit negativen Linearfaktoren im Nenner (mit positiven Polen) streben nach einer Systemerregung exponentiell einen theoretisch unendlich großen Wert an .

Die gleiche Übertragungsfunktion in Zeitkonstanten-Darstellung mit T_vi = - 1 / s_0i. Dabei ändert sich der Verstärkungsfaktor infolge der Division mit den Nullstellen.

$G(s)=K_{T}\cdot {\frac {\prod \nolimits _{i=1}^{m}\,(-{\frac {s}{s_{0i}}}+1)}{\prod \nolimits _{i=1}^{n}\,(-{\frac {s}{s_{i}}}+1)}}\,=\,K_{T}\cdot {\frac {\prod \nolimits _{i=1}^{m}\,(T_{vi}\cdot s+1)}{\prod \nolimits _{i=1}^{n}\,(T_{i}\cdot s+1)}}$

In der Produkt-Darstellung der Übertragungsfunktion können folgende Terme 1. Ordnung und 2. Ordnung mit konjugiert komplexen Nullstellen mehrfach auftreten:

• Produktterme 1. Ordnung (Linearfaktoren): s-s₁ oder in Zeitkonstanten-Darstellung umgerechnet: T*s+1
• Linearfaktoren ohne Absolutglied : s - 0 = s, in Zeitkonstanten-Darstellung: T*s
• Produktterme 2. Ordnung (mit konjugiert komplexen Nullstellen): s² + p*s + q,

In Zeitkonstanten-Darstellung: T²*s²+2*D*T*s+1

Diese 3 nicht mehr aufspaltbaren Teilsysteme (Linearfaktoren bzw. quadratischer Linearfaktor) haben ein völlig unterschiedliches Übertragungsverhalten im Zeit- und Bildbereich, ob sie im Nenner oder Zähler der Übertragungsfunktion stehen. Komplizierteste lineare Systeme höherer Ordnung setzen sich aus diesen Teilsystemen zusammen.

Linearfaktoren haben differenzierendes Verhalten, wenn sie im Zähler der Übertragungsfunktion stehen und integrierendes oder zeitverzögerndes Verhalten, wenn sie im Nenner stehen. Sie werden auch als phasenminimale oder reguläre Systeme bezeichnet.
Phasenminimumsysteme sind rationale Übertragungsfunktionen G(s) ohne Totzeit, die nur Pole und Nullstellen in der linken s-Halbebene haben:

Übertragungsglieder als Blockstruktur im Signalflussplan

Übertragungssysteme können aus Teilsystemen als Blöcke zusammengefasst werden. Es gilt das Superpositionsprinzip. Die Systeme in Produktdarstellung können in der Reihenfolge beliebig verschoben werden. Die Systemausgänge dürfen nicht durch nachfolgende Systemeingänge belastet werden (Rückwirkungsfreiheit).

• Parallelschaltung:

Gleichung der Übertragungsfunktion der Parallelschaltung:

$G\left(s\right)=G_{1}\left(s\right)+G_{2}\left(s\right)$

• Reihenschaltung:

Gleichung der Übertragungsfunktion der Reihenschaltung:

$G\left(s\right)=G_{1}\left(s\right)\cdot G_{2}\left(s\right)$

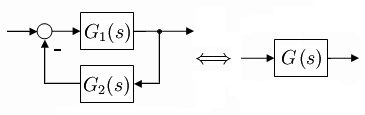
• Gegenkopplung oder Rückkopplung:

Gleichung der Übertragungsfunktion der Gegenkopplung:

$G\left(s\right)={\frac {G_{1}\left(s\right)}{1+G_{1}\left(s\right)\cdot G_{2}\left(s\right)}}$

• Gegenkopplung ohne Teilsystem in der Rückführung:

Bei einem Regelkreis, der in dem Gegenkopplungszweig kein statisches oder dynamisches Teilsystem enthält, wird das System G₂(s) = 1.

Damit lautet die Übertragungsfunktion des geschlossenen Regelkreises:

$G(s)={\frac {G_{1}(s)}{1+G_{1}(s)}}$

• Mitkopplung:

Eine Mitkopplung ist eine positive additiv wirkende Rückführung des Signalausgangs auf den Systemeingang. Sie führt je nach Größe der Verstärkung von G₁(s) zur monotonen Instabilität oder zu einem Hysterese-Effekt.

Gleichung der Übertragungsfunktion der Mitkopplung:

$G(s)={\frac {G_{1}(s)}{1-G_{1}(s)}}$

• Mit G₁(s) als offener Regelkreis werden beliebige algebraische Zusammenführungen der Teilsysteme des Reglers und der Regelstrecke verstanden.

Lineare Systeme mit verzögerndem Verhalten

Die nachstehenden Teilsysteme können beliebig im Zähler und Nenner einer Übertragungsfunktion G(s) entsprechend der Gesamtsystemstruktur multiplikativ und / oder additiv kombiniert werden.

• Integrierglied, Kurzform: I-Glied:

$G(s)={\frac {1}{T_{N}\cdot s}}\$

• Verzögerungsglied, Kurzform: PT1-Glied:

$G(s)={\frac {K}{T\cdot s+1}}\$

• Schwingungsglied, Kurzform: PT2-Glied_KK mit konjugiert komplexen Polen.

$G(s)={\frac {K}{(T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1)}}$

Lineare Systeme mit differenzierendem Verhalten

• Differenzierglied, Kurzform: D-Glied

$G(s)=T_{V}\cdot s\,$

• Proportional wirkendes D-Glied, Kurzform: PD1-Glied

$G(s)=K\cdot (T_{V}\cdot s+1)\,$

• Proportional wirkendes D-Glied 2. Ordnung mit konjugiert komplexen Polen, Kurzform: PD2-Glied_KK

$G(s)=K\cdot (T_{V}^{2}\cdot s^{2}+2\cdot D\cdot T_{v}\cdot s+1)$

Beispiel eines realisierbaren Übertragungssystems 3. Ordnung (Anzahl Pole > Nullstellen)

Beschreibung einer Übertragungsfunktion G(s) als gebrochene rationale Funktion in Produktdarstellung mit der Verstärkung K:

$G(s)={\frac {Y}{U}}(s)={\frac {K\cdot (T_{V1}\cdot s+1)\cdot (T_{V2}\cdot s+1)}{(T_{1}\cdot s+1)\cdot (T_{2}\cdot s+1)\cdot (T_{3}\cdot s+1)}}$

Die systembeschreibende Differenzialgleichung dieser Systeme zeigt Stabilität an, wenn alle Koeffizienten der einzelnen Terme positiv sind. (Mindestvoraussetzung der Stabilität). Die Übertragungsfunktionen dieser linearen Grundsysteme sind stabil, wenn die Vorzeichen der zugehörigen Nullstellen negativ sind.

Gleiche stabile Pole und Nullstellen der 3 Grundformen lassen sich in der Produktform (= Reihenschaltung der Systeme) gegeneinander kürzen und vereinfachen damit die Berechnung des Gesamtsystems. In der Produktform der Zeitkonstanten-Darstellung im Zähler und Nenner können die Teilsysteme gegeneinander gekürzt werden, wenn die Zeitkonstanten T_V = T sind.

Globales P-, I-, D-Systemverhalten

Wenn in einer systembeschreibenden Differenzialgleichung oder in der zugehörigen Übertragungsfunktion aus der geschlossenen Reihenfolge der Ableitungen bestimmte Koeffizienten fehlen, bzw. zu Null gesetzt sind, ergibt sich für das Gesamtverhalten im Zeitbereich folgendes typische Verhalten für den Linearfaktor ohne Absolutglied:

Sprungantworten des globalen P-, I-, und D-Verhaltens

Globales P-Verhalten

Im stationären Zustand ergibt diese Form der Übertragungsfunktion nach einem Eingangssprung für das Ausgangssignal mit der Verstärkung K ein P-Verhalten im Zeitbereich, weil alle Linearfaktoren vollständig sind:

$G(s)={\frac {K\cdot (T_{V1}\cdot s+1)\cdot (T_{V2}\cdot s+1)}{(T_{1}\cdot s+1)\cdot (T_{2}\cdot s+1)\cdot (T_{3}\cdot s+1)}}$

Nach dem Einschwingvorgang nach genügend langer Zeit ist die Ausgangsgröße:

$y(t)=\lim _{t\to \infty }K\cdot u(t)\,$

Globales I-Verhalten

Im stationären Zustand ergibt diese Form der Übertragungsfunktion nach einem Eingangssprung u(t) für das Ausgangssignal ein stetig wachsendes Ausgangssignal im Zeitbereich. Der Linearfaktor ohne Absolutglied befindet sich im Nenner.

$G(s)={\frac {K\cdot (T_{V1}\cdot s+1)\cdot (T_{V2}\cdot s+1)}{T_{1}\cdot s\cdot (T_{2}\cdot s+1)\cdot (T_{3}\cdot s+1)}}$

Nach dem Eingangssprung und genügend langer Zeit ist die Ausgangsgröße:

$y(t)=\lim _{t\to \infty }{\frac {K}{T_{1}}}\cdot t\cdot u(t)\,+t_{0}\,$

Globales D-Verhalten

Im stationären Zustand ergibt diese Form der Übertragungsfunktion nach einem Eingangssprung u(t) für die Ausgangsgröße y(t) den Wert 0. Der Linearfaktor ohne Absolutglied befindet sich im Zähler.

$G(s)={\frac {K\cdot T_{V1}\cdot s\cdot (T_{V2}\cdot s+1)}{(T_{1}\cdot s+1)\cdot (T_{2}\cdot s+1)\cdot (T_{3}\cdot s+1)}}$

Das Ausgangssignal y(t) lautet:

$y(t)=\lim _{t\to \infty }K\cdot T_{V1}\cdot 0=0\,$

Stabilität

Bedeutung der Pole und der konjugiert komplexen Polpaare in der linken und rechten s-Halbebene

• Ein dynamisches lineares oder nichtlineares System kann stabil oder instabil (monoton instabil oder oszillatorisch instabil) sein.
• Ein Regelkreis bestehend aus linearen oder nichtlinearen instabilen Teilsystemen kann mit geeigneten Reglern zum stabilen Verhalten gebracht werden.
• In einem Regelkreis mit einem Teilsystem mit Totzeit versagen die meisten Stabilitätskriterien, mit Ausnahme des grafischen Nyquist-Kriteriums für den "aufgeschnittenen" Regelkreis. Abhilfe: Numerische Berechnung des Systemverhaltens des Regelkreises für ein gegebenes Eingangssignal und tabellarische Darstellung der Berechnungsfolgen des Ausgangssignals im diskreten Zeitbereich.
• Der Übertragungsfunktion eines Systems $G_{1}(s)$ kann die transzendente Funktion des Totzeitgliedes $G_{Tt}(s)=e^{-s\,T_{t}}$ multiplikativ angehängt werden zu $G(s)=G_{1}(s)\cdot G_{Tt}(s)$. Diese Form der Übertragungsfunktion als Gesamtsystem ist nur für Frequenzgang-Analysen geeignet. Eine algebraische Berechnung mit dieser Gleichungsform ist nicht möglich.

Die nachfolgenden Beschreibungen beziehen sich auf Systembeschreibungen der Übertragungsfunktion als gebrochen-rationale Funktion, die sich laut Definition immer linear verhalten muss.

Interne Stabilität:

Wenn die Übertragungsfunktion eines Übertragungssystems oder eines Regelkreises vorliegt:

Die Pole einer Übertragungsfunktion bestimmen die Stabilität und die Geschwindigkeit der Systembewegung. Die Nullstellen einer Übertragungsfunktion haben nur Einfluss auf die Amplituden des Systems.

Ein Übertragungssystem ist intern stabil, wenn alle (Teil-)Übertragungsfunktionen nur Pole in der linken s-Halbebene haben.

Beispiel für die Darstellung der externen Stabilität (BIBO-Stabilität) bei verschiedenen Systemen

Asymptotische Stabilität:

Bedeutung: Das Ausgangssignal eines linearen dynamischen Systems im Zeitbereich strebt nach einer "Einschwingzeit" als Folge eines Eingangssignals einen stabilen Zustand auf das Niveau des Eingangssignals mit der Verstärkung K * u(t) an.

Bedingungen der asymptotischen Stabilität: Sämtliche Pole des charakteristischen Polynoms der Übertragungsfunktion müssen negativ sein. Sämtliche Pole des charakteristischen Polynoms müssen von Null verschieden sein, d.h. es dürfen keine Teilsysteme mit I-Verhalten (Integrator) enthalten sein. Es dürfen keine Mehrfachpole im Ursprung der s-Ebene auftreten (d.h. mehrere Integratoren). Die Anzahl der Nullstellen der charakteristischen Polynome im Zähler und Nenner der Übertragungsfunktion muss kleiner als die der Pole sein.

Bedeutung der Pole für das Systemverhalten bei einfachen Polen und konjugiert komplexen Polenpaaren:

• Lage aller Pole des Übertragungssystems in der linken s-Halbebene:

System ist asymptotisch stabil.

• Lage eines Poles des Übertragungssystems in der rechten s-Halbebene:

System ist monoton instabil.

• Lage eines Poles des Übertragungssystems auf der imaginären Achse (Realteil = 0) der s-Ebene:

System ist grenzstabil.

• Lage mehrfacher Pole auf der imaginären Achse der s-Ebene:

System ist instabil.

• Konjugiert komplexe Polpaare mit negativem Realteil:

System ist asymptotisch stabil, die Schwingneigung ist von der Dämpfung D abhängig.

• Konjugiert komplexe Polpaare mit einem Realteil gleich oder größer Null:
• System verhält sich monoton instabil oder oszillatorisch instabil.

Externe Stabilität (BIBO-Stabilität)

Wenn die Hardware eines Übertragungssystems bzw. eines Regelkreises oder eines genauen Modells mit dem Eingangs- und Ausgangssignal vorliegt:

Ein Übertragungssystem gilt als extern stabil, wenn jedes beliebige beschränkte Eingangssignal an dem System auch ein beschränktes Ausgangssignal hervorruft. (BIBO-Stabilität)

Lineare phasenminimale und nichtphasenminimale Übertragungssysteme

Phasenminimumsystem (reguläres System)

Bei stabilen dynamischen Übertragungssystemen sind die Koeffizienten der systembeschreibenden gewöhnlichen Differenzialgleichung positiv bzw. die Nullstellen und Pole der Übertragungsfunktion negativ.

• Phasenminimumsysteme sind Übertragungssysteme ohne Totzeit, bei denen die Übertragungsfunktion G(s) nur Pole und Nullstellen in der linken s-Halbebene hat.

• Für einen gegebenen Amplitudengang hat das Phasenminimumsystem eine minimale Phasenverschiebung. Die Kenntnis des Amplitudengangs genügt, um auf die Übertragungsfunktion des Systems schließen zu können.

• Nicht alle Phasenminimumsysteme sind stabil. Sie erfüllen alle den Begriff der "Internen Stabilität" aber nicht alle sind "Extern stabil".

Nichtphasenminimumsystem (nichtreguläres System)

Ein dynamisches Übertragungssystem hat ein nichtminimales Phasenverhalten, wenn es eine Totzeit enthält oder die Pole oder Nullstellen der Übertragungsfunktion in der rechten Seite der s-Halbebene liegen. Der Phasenverlauf des Übertragungssystems ist betragsmäßig größer, als es bei einem phasenminimalen System mit gleichem Amplitudengang wäre.

Zusammenfassung der Eigenschaften der Nichtphasenminimumsysteme:

• Nichtphasenminimumsysteme enthalten eine Totzeit oder Pole oder Nullstellen in der rechten s-Halbebene.
• Nichtphasenminimumsysteme mit Polen in der rechten s-Halbebene sind instabile Systeme. Dieses System reagiert auf ein Eingangssignal mit einem unbeschränkten Ausgangssignal.
• Nichtphasenminimumsysteme mit Polen in der rechten s-Halbebene und Phasenminimumsysteme sind relativ leicht zu regeln.
• Nichtphasenminimumsysteme mit Nullstellen in der rechten s-Halbebene (Allpass-Systeme) sind stabile Systeme aber sehr schwierig zu regeln.
• Nullstellen in Phasenminimumsystemen und Nichtphasenminimumsystemen haben Einfluss auf die Amplituden der Ausgangssignale. Pole bestimmen das Zeitverhalten.

Nichtphasenminimum-Verhalten wird durch Totzeitglieder oder Allpassglieder in Serie mit Phasenminimumsystemen verursacht. Dieses Verhalten kann durch Differenzbildung von phasenminimalen Systemen oder durch positive Rückkopplung in einem Regelkreis entstehen. In der Natur können nichtphasenminimale Systeme entstehen, wenn z. B. auf die Lage einer Masse Beschleunigungskräfte einwirken, wie sie durch die Gravitation oder durch den Magnetismus hervorgerufen werden. Die Lage der Masse wird zunehmend beschleunigt und wächst progressiv bis zu einer natürlichen Begrenzung. Klassische Beispiele solcher Systeme sind: Invertiertes Pendel, Magnetschwebekörper, Laufkatze am Hebekran.

Ein nichtminimalphasiges System ist immer zerlegbar in eine Reihenschaltung bestehend aus Phasenminimumsystem und Allpass.

Instabile nichtphasenminimale Systeme beziehen sich auf Verzögerungsglieder 1. und 2. Ordnung:

$G(s)={\frac {K}{1-T\cdot s}}\qquad {\text{und}}\quad G(s)={\frac {K}{1-(T_{1}+T_{2})\cdot s+T_{1}\cdot T_{2}\cdot s^{2}}}$

Allpassglieder

Allpassglieder sind multiplikative Kombinationen von instabilen PD1-Gliedern (positive Nullstelle im Zähler) und stabilen PT1-Gliedern (negativer Pole im Nenner) der Übertragungsfunktion.

Sie reagieren auf einen Eingangssprung u(t) zunächst mit einem Sprung entgegengesetzter Polarität, um sich dann asymptotisch auf das Niveau des Sprungs einzustellen.

$G(s)=K\cdot {\frac {1-T_{1}\cdot s}{1+T_{1}\cdot s}}$

Allpassglieder können durch Subtraktion eines PT1-Gliedes von einem DT1-Glied entstanden sein (= Parallelschaltung zweier Übertragungsfunktionen).

$G(s)=K\cdot {\frac {1-T_{1}\cdot s}{1+T_{1}\cdot s}}=K\cdot \left({\frac {1}{1+T_{1}\cdot s}}-{\frac {T_{1}\cdot s}{1+T_{1}\cdot s}}\right)$

Allpassglieder sind Systeme, die für alle Frequenzen einen konstanten Amplitudengang haben. Lediglich die Phase eilt mit unterschiedlicher Abhängigkeit von ω nach.

$|G(j\omega )|=1\,$

Die Sprungantwort des Allpassgliedes im Zeitbereich nach der inversen Laplace-Transformation lautet:

$g(t)=K\cdot (1-2\cdot e^{-{\frac {t}{T_{1}}}})$

Totzeitglied

Das Totzeitglied verschiebt ein Eingangssignal u(t) um den Betrag der Totzeit T_t, ohne das Signal zu verformen.

Beispiel von Totzeitsystemen: Fördermengen mit dem Transportband, Lange Gasdruckleitungen, Spiel in Getriebeübersetzungen, Umschaltvorgänge bei Ventilen und andere Schaltvorgänge und Signallaufzeiten.

Im Gegensatz zu den linearen dynamischen Übertragungssystemen kann ein Totzeitsystem nicht mit einer gewöhnlichen Differenzialgleichung, sondern nur mit einer partiellen Differenzialgleichung beschrieben werden. Laufzeitglieder oder Totzeitglieder gehören zu der Klasse der Systeme mit verteilten Parametern. Sie haben keine konzentrierten Speicher und keine Pole und Nullstellen in der endlichen s-Ebene.

Einen wesentlich einfacheren Zusammenhang zwischen der Ein- und Ausgangsgröße eines Totzeitsystems gewinnt man durch die Darstellung der Totzeit mit der Übertragungsfunktion.

Zeitverhalten des Totzeitgliedes:

$\displaystyle y(t)={u}(t-T_{t})$

Sprungantwort:

${\text{für}}\quad t<T_{t}\quad y(t)=0\;$

${\text{für}}\quad t\geq T_{t}\quad y(t)=1\;$

Übertragungsfunktion des Totzeitgliedes:

Die Beziehung des Eingangs- und Ausgangsverhaltens des Totzeitsystems wird durch den Verschiebesatz der Laplace-Transformation wiedergegeben:

$G(s)={\frac {Y}{U}}(s)=e^{-s\cdot T_{t}}$

Für Übertragungssysteme mit einem Totzeitglied wird dem linearen System G₁(s) die transzendente Funktion des Totzeitgliedes multiplikativ beigefügt:

$G(s)={\frac {Y}{U}}(s)=G_{1}(s)\cdot e^{-s\cdot T_{t}}$

Sprungantwort eines Systems mit Totzeit Tt = 2 s und vier in Reihe geschalteten PT1-Gliedern mit je T = 1 s für einen Ansprung und Rücksprung

Diese Darstellungsform eines Totzeitgliedes bzw. Kombinationen linearer dynamischer Systeme mit einem Totzeitverhalten als Übertragungsfunktion eignet sich für Analysen der Stabilität nur im Frequenzbereich. Dabei kommen grafische Stabilitätsverfahren wie das Bode-Diagramm oder die Ortskurve des Frequenzgangs zur Anwendung.

Beispiel

Gegeben: System mit 4 Verzögerungsgliedern je T = 1 s und Totzeitglied Tt = 2 s $G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{(s+1)^{4}}}\cdot e^{-2\cdot s}$ Das grafische Beispiel eines Verzögerungssystems mit Totzeit zeigt den numerisch berechneten Verlauf der Ausgangsgröße y(t) für einen Eingangssprung $u(t)=1\quad \left(U(s)={\frac {1}{s}}\right)$ und Rücksprung u(t) = 0.

Padé-Approximation

Ein Totzeitglied kann als ein Allpassglied unendlicher Ordnung zu einem System mit gebrochener rationaler Übertragungsfunktion angenähert werden. Dieses Verfahren ist unter der Padé-Approximation bekannt. Die Genauigkeit der Annäherung hängt von der Ordnung des Allpassgliedes ab.

Padé-Approximation 1. und 2. Ordnung:

$G_{1}(s)=e^{-s\cdot T_{t}}\,\approx \,{\frac {1-{\frac {T_{t}}{2}}\cdot s}{1+{\frac {T_{t}}{2}}\cdot s}}\qquad G_{2}(s)=e^{-s\cdot T_{t}}\,\approx \,{\frac {1-{\frac {T_{t}}{2}}\cdot s+{\frac {T_{t}^{2}}{12}}\cdot s^{2}}{1+{\frac {T_{t}}{2}}\cdot s+{\frac {T_{t}^{2}}{12}}\cdot s^{2}}}$

Der Nachteil dieser Form der Polynomdarstellung 2. Ordnung ist die erforderliche zusätzliche Rechenarbeit zur faktoriellen Darstellung. Für jede Änderung des Wertes der Totzeit müssen für die faktorielle Darstellung die Nullstellen und Pole berechnet werden. Je nach Größe der Totzeit können auch konjugiert komplexe Pole und Nullstellen entstehen.

Folgende Gleichung der modifizierten Padé-Approximation erlaubt die Berechnung der Annäherung an die Totzeit durch gleiche Allpassglieder beliebiger Ordnung n:

$G_{n}(s)=e^{-s\cdot T_{t}}\,\approx \,{\biggl (}{\frac {1-{\frac {T_{t}}{2\cdot n}}\cdot s}{1+{\frac {T_{t}}{2\cdot n}}\cdot s}}{\biggr )}^{n}$

Totzeitapproximation mit einem Allpass 3. Ordnung.

Die Padé-Approximation der Totzeit bringt bereits bei drei identischen Allpassgliedern (n = 3) gute Ergebnisse der Totzeit-Annäherung.

Der Allpass mit einem PD-Glied im Zähler mit einer positiven Nullstelle kann wie folgt in bekannte Teilsysteme 1. Ordnung als PT1-Glied und D-Glied zerlegt werden:

Beispiel von drei identischen Allpassgliedern in Reihenschaltung mit dem Proportionalfaktor K:

$G_{3}(s)\approx K\cdot {\biggl (}{\frac {1-{\frac {T_{t}}{6}}\cdot s}{1+{\frac {T_{t}}{6}}\cdot s}}{\biggr )}^{3}=K\cdot {\biggl (}{\frac {1}{1+{\frac {T_{t}}{6}}\cdot s}}-{\frac {{\frac {T_{t}}{6}}\cdot s}{1+{\frac {T_{t}}{6}}\cdot s}}{\biggr )}^{3}$

Für die numerische Berechnung (Eulersches Streckenzug-Verfahren) ergeben sich pro Allpass folgende drei Gleichungen, die hintereinander pro Berechnungsfolge zu berechnen sind:
(Jedes Ausgangssignal y_(k) ist das Eingangssignal u_(k) der nächsten Gleichung innerhalb einer Folge)

$\mathrm {PT_{1}} -{\text{Glied:}}\quad y1_{(k)}=y_{(k-1)}+[u_{(k)}-y_{(k-1)}]\cdot {\frac {6\cdot \Delta t}{T_{t}}}$

${\text{D-Glied:}}\ \ \ \qquad y2_{(k)}=[u_{(k)}-u_{(k-1)}]\cdot {\frac {T_{t}}{6\cdot \Delta t}}$

${\text{Subtraktion:}}\ \quad y_{(k)}=K\cdot [y1_{(k)}-y2_{(k)}]\,$

Für die numerische Berechnung der Reihenschaltung von 3 Allpässen sind damit 9 Gleichungen pro Berechnungsfolge erforderlich.

Bei Anwendung der Tabellenkalkulation durch die INDEX-Anweisung: „INDEX (Bezug: Spalte; Bereich)“ wird ein Index verwendet, um aus einem Bezug einen Wert zu wählen. Damit ist für die exakte Totzeit-Berechnung nur eine Gleichung pro Berechnungsfolge erforderlich.

Zurück zum Inhaltsverzeichnis