Entropie: Information
Zurück zur Übersicht
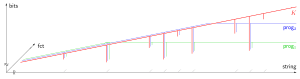
Zusammenhang zwischen Entropie und Information
[Bearbeiten]Zitat: Man kann Philosophen in zwei Klassen einteilen: die einen glauben, daß sich die Philosophen in zwei Klassen einteilen lassen, die anderen nicht. ( Von Anonymus)
Über den genauen Zusammenhang zwischen der Entropie und der Information wird heftig diskutiert:
Vorschläge
[Bearbeiten]I = k * E
- Shannon
- Information und Entropie sind direkt proportional
I = - k * E

- Schrödinger, Wiener , Slizard, Brillouin
- Information und Entropie sind indirekt proportional
- beispielsweisen in Léon Brillouin
- Science and Information Theory (New York: Academic Press, 1956)
Brillouin [1951a] p. 335 : Shannon, however compares information with positive entropy, a procedure which seems difficult to justify since information is lost during the process of transmission, while entropy is increased.
I = Io* e^(-k*E)
- Tom Stonier
- Information und Entropie sind negativ korreliert, es gibt negative Entropie
- https://web.archive.org/web/20130223042705/http://www.madeasy.de/2/stonier.htm
Wer hat hier recht ?
Gesamtinformation = Entropie + geordnete Information
[Bearbeiten]Ein weiterer Vorschlag wäre folgender:
Wenn man die Entropie als quantitatives Maß für die Zufallsinformation betrachtet , die in einem System steckt, dann kann man sagen, dass die Gesamtinformation des Systems immer größer oder gleich der Entropie des Systems ist.
Es gilt wahrscheinlich folgende Formel:
Gesamtinformation = Zufällige Information
+ nichtzufällige Information
So kann man beispielsweise die berühmten Reihen von Chaitin einfach zusammenkleben und erhält dann eine neue IO Sequenz, dessen Informationsgehalt der Summe aus beiden Einzelsequenzen entspricht :
Informationsgehalt von 0110110011011110001010101010101010101010 = Informationsgehalt von 01101100110111100010 + Informationsgehalt von 10101010101010101010
Aufspaltung der binären Zahlen in geordnete Folgen und zufällige Folgen
[Bearbeiten]Das binäre Zahlensystem zeigt uns eine universelle Methode, um Informationen darzustellen. Viele grundlegende Eigenschaften des Informationsbegriffes lassen sich in der binären Darstellung leichter verstehen, als in anderen Codierungen. So kann man sich im binären Zahlensystem auch klar machen, wie sich geordnete Muster von zufälligen Mustern unterscheiden. Am besten stellt man sich die binäre Informationswelt als ein Dreieck vor , das an seiner Basis sehr schnell breiter wird, je länger die binären Folgen werden. An der Spitze des Dreiecks stehen dann zwei Folgen mit nur einer Stelle, nämlich 0 und 1. Je länger die binären Folgen, desto breiter wird das Dreieck und die Zahl der Möglichkeiten.
1 , 0
00, 01, 10, 11
000,001,010,011,100,101,110,111
0000,0001,0010,0011,0100,0101,0110,0111,1000,1001,1010,1011,1100,1101,1110,1111
00000,00001,00010,00011,00100,00101,00110,00111,01000,01001,01010,01011,01100,01101,01110,01111, 10000,10001,10010,10011,10100,10101,10110,10111,11000,11001,11010,11011,11100,11101,11110,11111
Die Zahl der Möglichkeiten wächst mit zwei hoch der Länge der Folge. Z = 2^Länge
Länge Zahl der Möglichkeiten -------------------------------------------------- 1 2 2 4 3 8 4 16 5 32 6 64
Die eigene Anschauung läßt einen in diesen Folgen sehr einfach geordnete und ungeordnete Sequenzen erkennen. Allerdings macht diese Unterscheidung erst ab einer gewissen Länge einen Sinn. Bei der Länge 1 oder der Länge 2 gibt es noch keinen Unterschied zwischen Ordnung und Zufall. Auch bei der Länge 3 ist die Unterscheidung noch nicht wirklich sinnvoll.
Unter den binären Folgen mit einer Länge von 6 Stellen kann man folgende hoch geordnete Sequenzen finden: 000000,101010,010101,111111 Die Entropie dieser vier Folgen ist, wenn man sie statisch berechnet, sehr niedrig. Alle übrigen 60 Folgen sind mehr oder minder ungeordnet und haben eine höhere Entropie. Die maximale Entropie einer binären Sequenz entspricht ihrer Länge.
Führt man diese Betrachtung für immer längere binäre Sequenzen durch, dann erkennt man die scheinbar regellose Mischung aus Ordnung und Entropie, die darin zum Vorschein kommt. Man sieht auch die mehr oder minder willkürliche Grenze zwischen beiden Bereichen. Hat man allerdings eine hochgeordnete Sequenz vor sich, dann ist auch im statistischen Test die Entropie als sehr niedrig zu berechnen. Umgekehrt ist bei einer binären Zufallsfolge die Entropie sehr hoch und die statistische Aussage dazu kaum anzuzweifeln.
Siehe auch Entropie:_IT#Die_Entropie_beliebiger_bin.C3.A4rer_Folgen (Die Entropie beliebiger binärer Zahlen)
Man kann für die binäre Welt feststellen:
- Die Entropie macht bei der Betrachtung von kurzen Sequenzen noch keinen Sinn.
- Der Übergang von geordneten Sequenzen zu ungeordneten Sequenzen ist mit zunehmender Länge je nach statistisch festgelegtem Signifikanzniveau des gewählten Testverfahrens mehr oder minder willkürlich. Allerdings wird die Unterscheidung immer klarer und zweifelsfreier je länger die Sequenzen sind und je geordneter ihre Struktur ist.
- In einem großen Meer der binären Unordnung gibt es Inseln der binären Ordnung.
- Es gibt zwei einfache Arten der binären Ordnung, die symmetrische Ordnung zb 111000 und die wiederholende Ordnung 101010.
Reale Beispiele an der Grenze von Ordnung und Entropie
[Bearbeiten]Am besten kann man sich die Bedeutung der Formel
Gesamtinformation = geordnete Information + Entropie.
an Beispielen klar machen, bei denen ein System zwischen verschiedenen Ordnungszuständen hin und her pendelt. Interessant ist auch die mathematische Berechnung der Struktur von Schneekristallen und die physikalische Messung ihrer Schmelzwärme.
Schneeflockenbeispiel
[Bearbeiten]Die mathematische Entropie einer Schneeflocke kann man aus ihrer Struktur berechnen. Die physikalische Entropie kann man über die Schmelzwärme messen, die zum Schmelzen der Schneeflocke gebraucht wird. So kann man aus der gegenüber einem Monokristall reduzierten Schmelzwärme einer Schneeflocke auf deren mathematischen Ordnungsgrad schlußfolgern und vielleicht einen Umrechnungsfaktor zwischen der physikalischen und der informationstheoretischen Entropie berechnen. Die Einheit dafür wäre bit / Joule / Kelvin.
Eis und Wasser
[Bearbeiten]Die Information eines Eisblockes, der auftaut und wieder gefriert, bleibt in seiner Gesamtinformation konstant. Die Menge an Zufallsinformation pendelt dabei zwischen einem hohen und einem geringen Wert hin und her. Die Menge an nichtzufälliger Information verhält sich dazu gegensinnig. Nicht zu vernachlässigen ist dabei natürlich der Zu- und Abstrom von Wärme von außen, ohne die kein Wechsel zwischen den Aggregatszuständen des Wassers stattfinden würde.
Planetensystem
[Bearbeiten]Betrachtet man das Sonnensystem, dann hat es gegenüber dem Eisblock den Vorteil, daß man es sich in grober Näherung von außen isoliert vorstellen kann. Stehen dann alle Planeten in einer Reihe auf einer Seite der Sonne, dann ist die Entropie sicher niedriger und der Anteil an geordneter Information größer, als bei einem Zustand der zufälligen Verteilung der Planeten um die Sonne. Das System der Planeten unterliegt zwar im Gegensatz zum Eisblock zumindest theoretisch keinem äußeren Einfluß durch eine periodische Energiezufuhr oder -abführung. Dennoch ist es physikalisch nicht ideal, da die Sonne ständig durch die Fusion Energie erzeugt und das Gesamtsystem so einen Massen- und Energieverlust erleidet.
Erkaltetes Planetensystem
[Bearbeiten]Um das Problem schwer berechenbarer Einflüsse durch die Kernfusion zu vermeiden, kann man ein Planetensystem mit einem erkalteten, ruhigen Zentralkörper betrachten der von 2,3 oder mehreren kleinen Planeten umkreist wird. Hier kann man dann, unter Vernachlässigung aller äußeren Einflüsse, die Entropie einer geordneten Konstellation, in der alle Planeten in einer Reihe auf einer Seite des Zentralgestirns stehen mit der Entropie einer weniger geordneten Konstellation vergleichen. So kann man eine einfache Formel für das hin und her pendeln zwischen Ordnung und Entropie finden und die Gesamtinformation errechnen.
Gesamtes Universum
[Bearbeiten]Vielleicht ist auch das gesamte Universum so etwas wie ein Entropiependel. Dann wäre zumindest einigermassen erklärbar, warum am Anfang ein Zustand so niedriger Entropie vorlag und die Entropie momentan ständig zunimmt. Der Urknall war dann nur der eine Umschlagspunkt des Entropiependels mit maximaler Ordnung und minimaler Entropie. Dieser strebt über Jahr Milliarden zum Punkt maximaler Entropie und minimaler Ordnung. Um dann wieder in die andere Richtung umzukehren. Dies wäre eine angenehmere Vorstellung, für alle die sich mit der Vorstellung des Wärmetodes des Universums nicht abfinden können.
Basisbegriffe der Natur- und Strukturwissenschaften
[Bearbeiten] Materie ------------ Energie
\ /
\ /
\ /
\ /
Information
/ \
/ \
/ \
/ \
/ \
Zufalls- geordnete
Information Information
| |
| |
| |
Beispiel: Beispiel:
01101100110111100010 10101010101010101010
| |
| |
| |
Stochastik Restliche Mathematik
Statistik
geordnete Information
/ \
/ \
/ \
/ \
/ \
symmetrisch wiederholend
geordnet geordnet
| |
| |
| |
| |
Beispiel: Beispiel:
00001111 10101010

- Hohe Entropie ist eher langweilig.
- Eine Ordnung ohne jeden Zufall ist auch eher langweilig.
>> Interessant ist die Mischung aus Entropie und Ordnung.
Wenn man 1 Gramm Wasser betrachtet, dann ist ein Wassertropfen mit Zufallsstruktur der Wassermoleküle eher langweilig. Ein geordneter Einkristall des Wassers ist auch langweilig (wenn es so etwas gibt). Interessant ist es zwischen drin: beispielsweise ein Schneekristall. Hier gibt es eine große Vielfalt der Formen.
